Stereometrické problémy
Problém 1
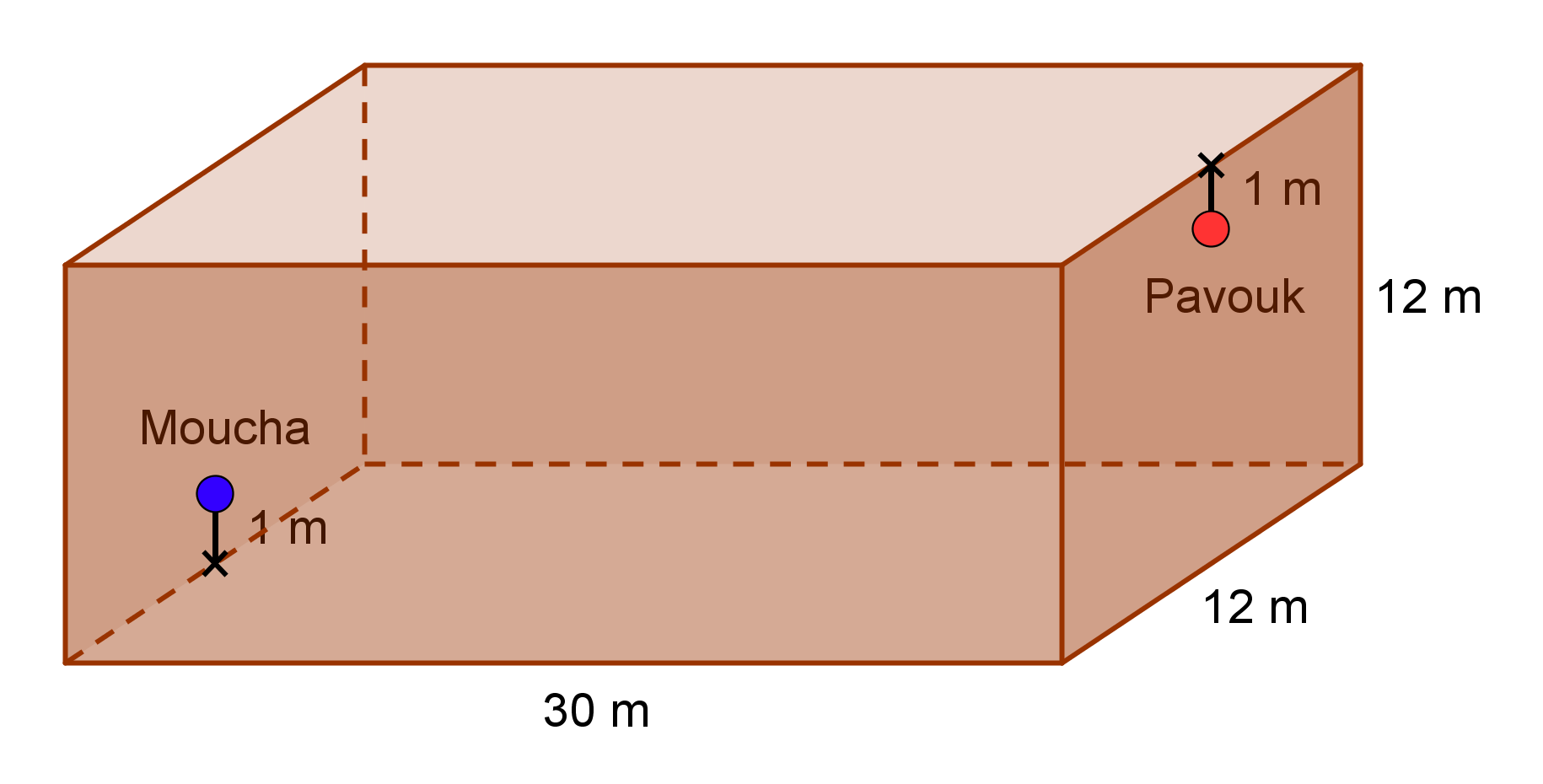
Na obrázku je místnost, v níž se nachází pavouk a moucha. Pavouk spočívá na svislé ose boční (z našeho pohledu) stěny místnosti (o rozměrech 12 krát 12 m) jeden metr pod stropem, moucha potom sedí na protilehlé stěně, opět na její svislé ose, tentokrát však jeden metr nad podlahou. Určete, jakou nejkratší vzdálenost musí pavouk překonat, pokud se chce dostat k mouše.
Nejprve uvažujte, že pavouk dojde k mouše výhradně pěšky, bez použití pavučiny. Přitom se může pohybovat po stěnách, podlaze i stropu místnosti.
Poté můžete vymyslet, jak si vzdálenost, kterou musí urazit pěšky, může zkrátit pomocí spuštění po pavučině.
Poznámka: Autorem této hádanky je anglický matematik a hádankář Henry Dudeney (1857 - 1930)
Problém 2
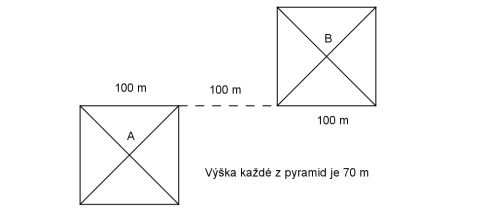
Určete délku nejkratší cesty, kterou bychom se dostali z vrcholu pyramidy A na vrchol pyramidy B. Pohybujeme se pěšky.
[Výpočet v programu wxMaxima]