Prémiové úlohy z geometrie (2017-2020)

Prémiové úkoly zadávané v předmětech Planimetrie a Geometrie II v letech 2017-2020

1. Libovolný trojúhelník ABC je svými středními příčkami rozdělen na 4 trojúhelníky, viz obrázek (trojúhelník A₁B₁C₁ nazýváme příčkový trojúhelník). Vyslovte tvrzení o vztahu těchto trojúhelníků navzájem i vzhledem k trojúhelníku ABC. Zaměřte se konkrétně na vztahy shodnosti, podobnosti a na poměry obsahů. Svá tvrzení dokažte. (PLA-2017/PU2)

   

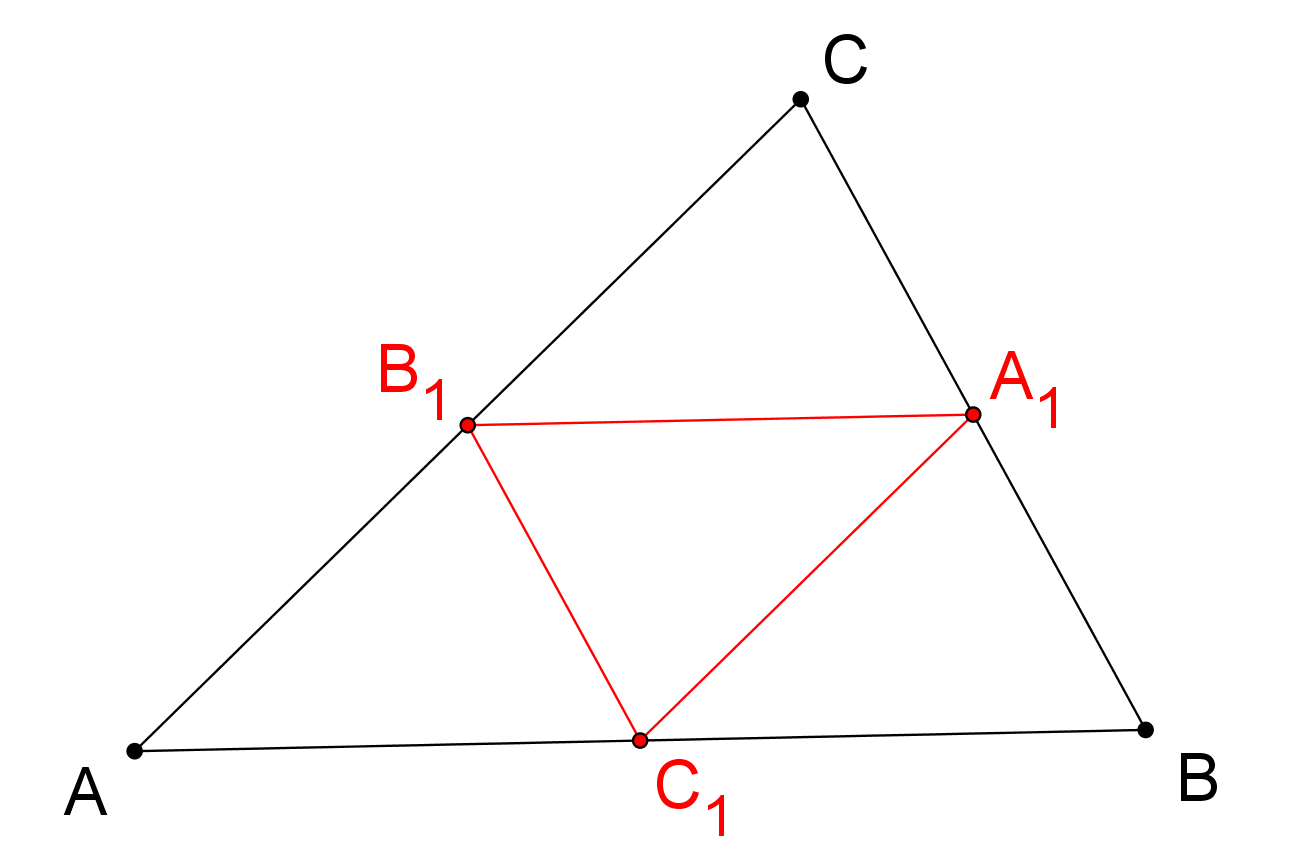
2. V libovolném lichoběžníku ABCD označme průsečík jeho úhlopříček E, viz obrázek. Potom trojúhelníky ADE a BCE mají shodné obsahy. Dokažte! (PLA-2017/PU3)

   

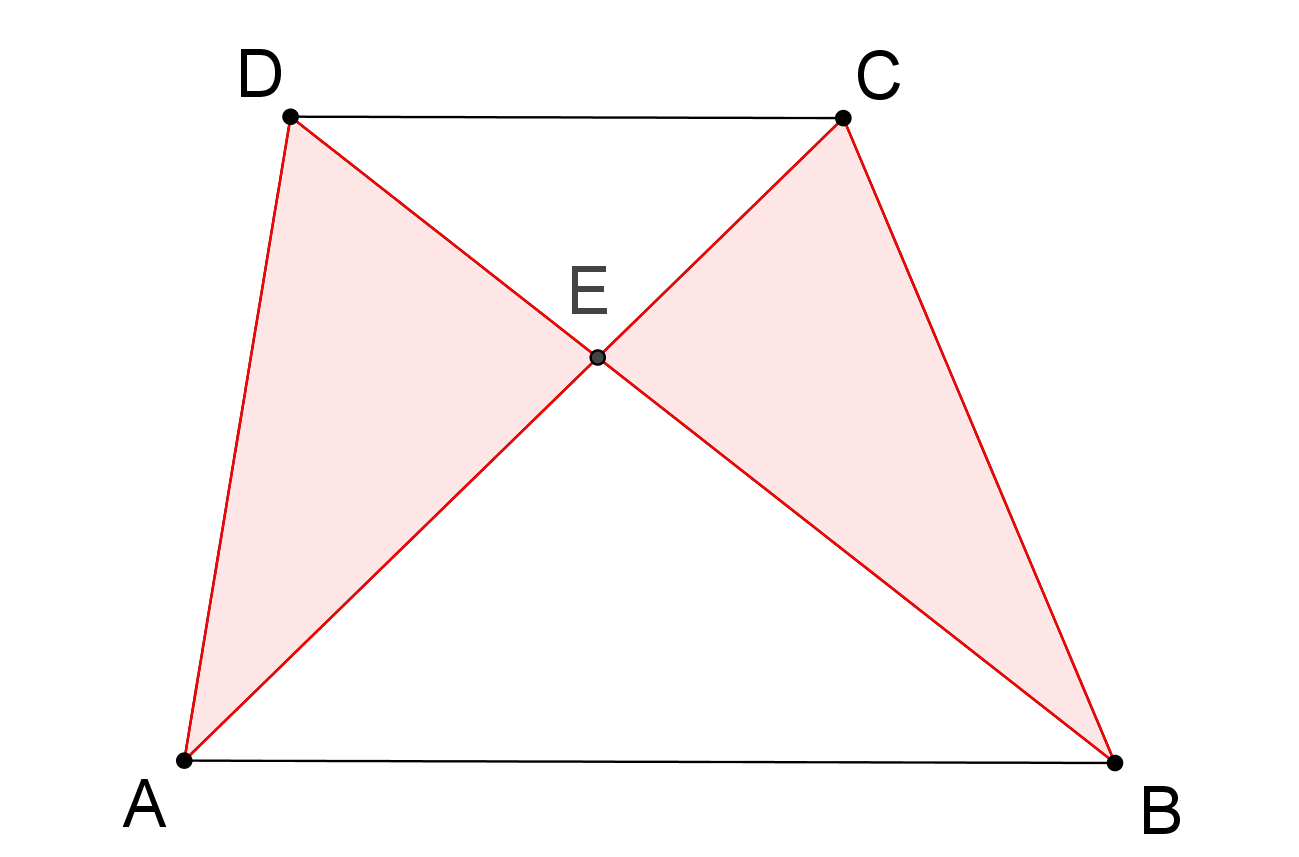
3. Pro libovolný čtverec ABCD s vrcholem A na ose y a s k němu sousedním vrcholem B na ose x platí, že souřadnice jeho středu S (viz obrázek) jsou buď čísla shodná nebo opačná. Dokažte! (PLA-2017/PU4)

   

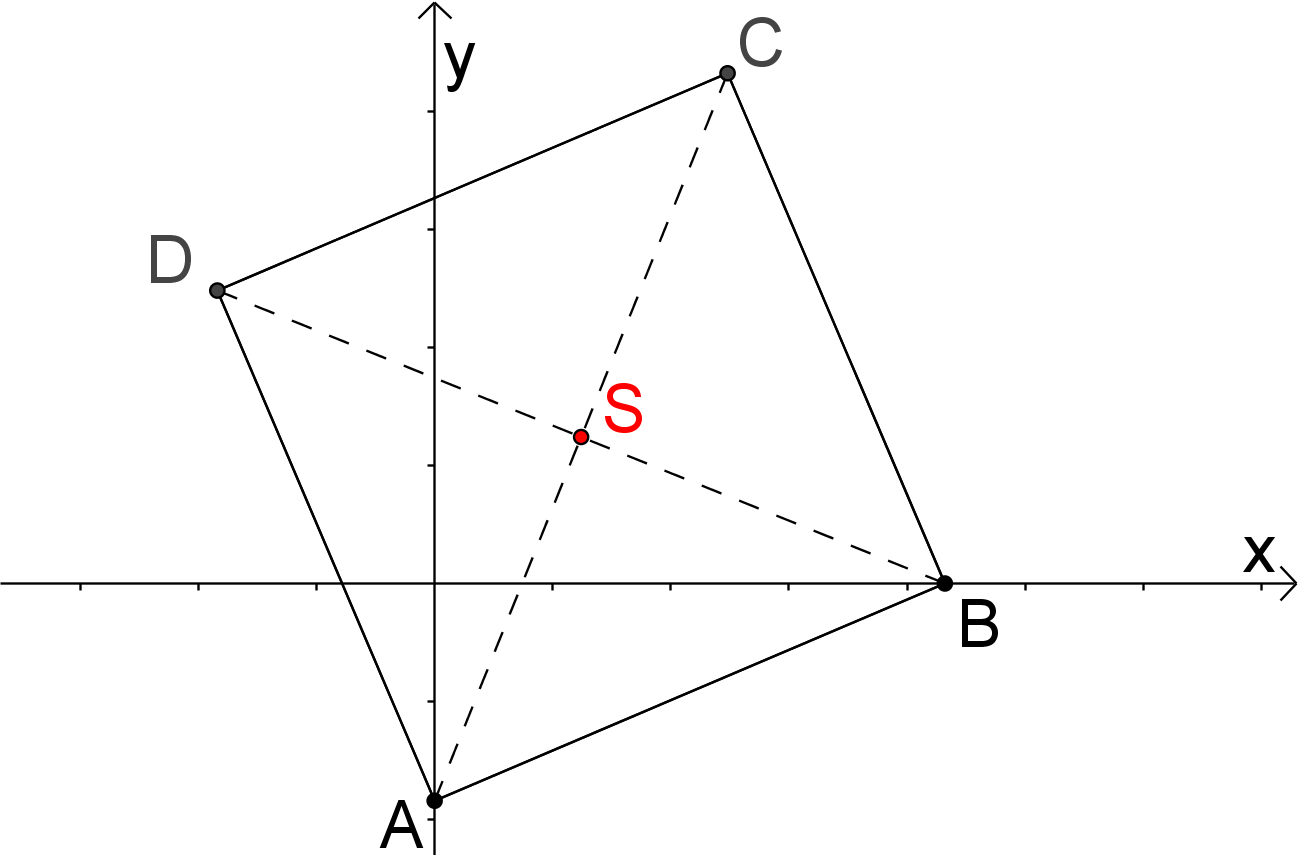
4. V libovolném lichoběžníku ABCD označme průsečík jeho úhlopříček E a veďme tímto bodem příčku FG rovnoběžnou s jeho základnami, viz obrázek. Potom bod E je středem této příčky. Dokažte! (PLA-2017/PU5)

   

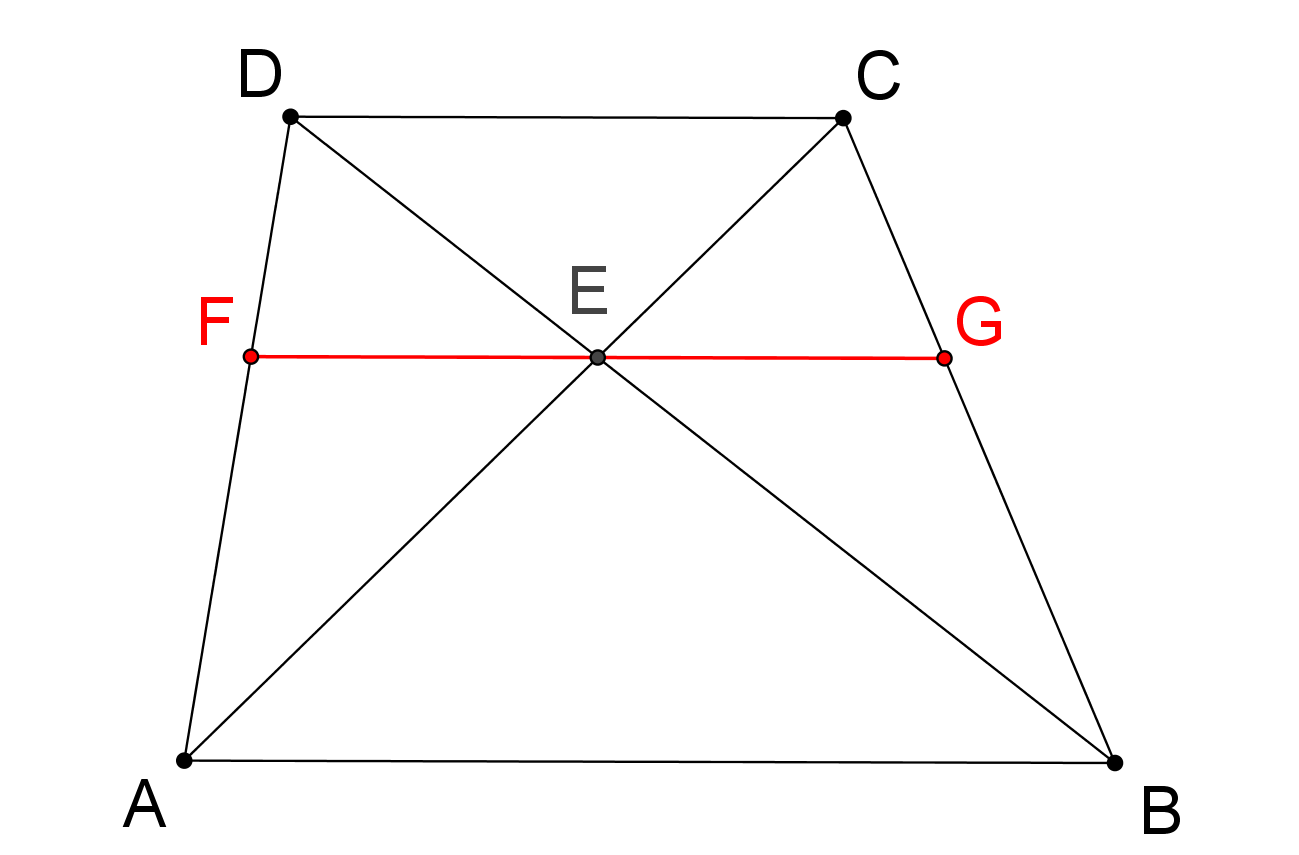
5. Na obrázku vidíme obrazec, který vznikne spojením větší půlkružnice s dvěma menšími stejně velkými půlkružnicemi. Dokažte, že každá přímka p jdoucí bodem O rozděluje obvod tohoto obrazce na dvě stejné části! (PLA-2017/PU6)

   

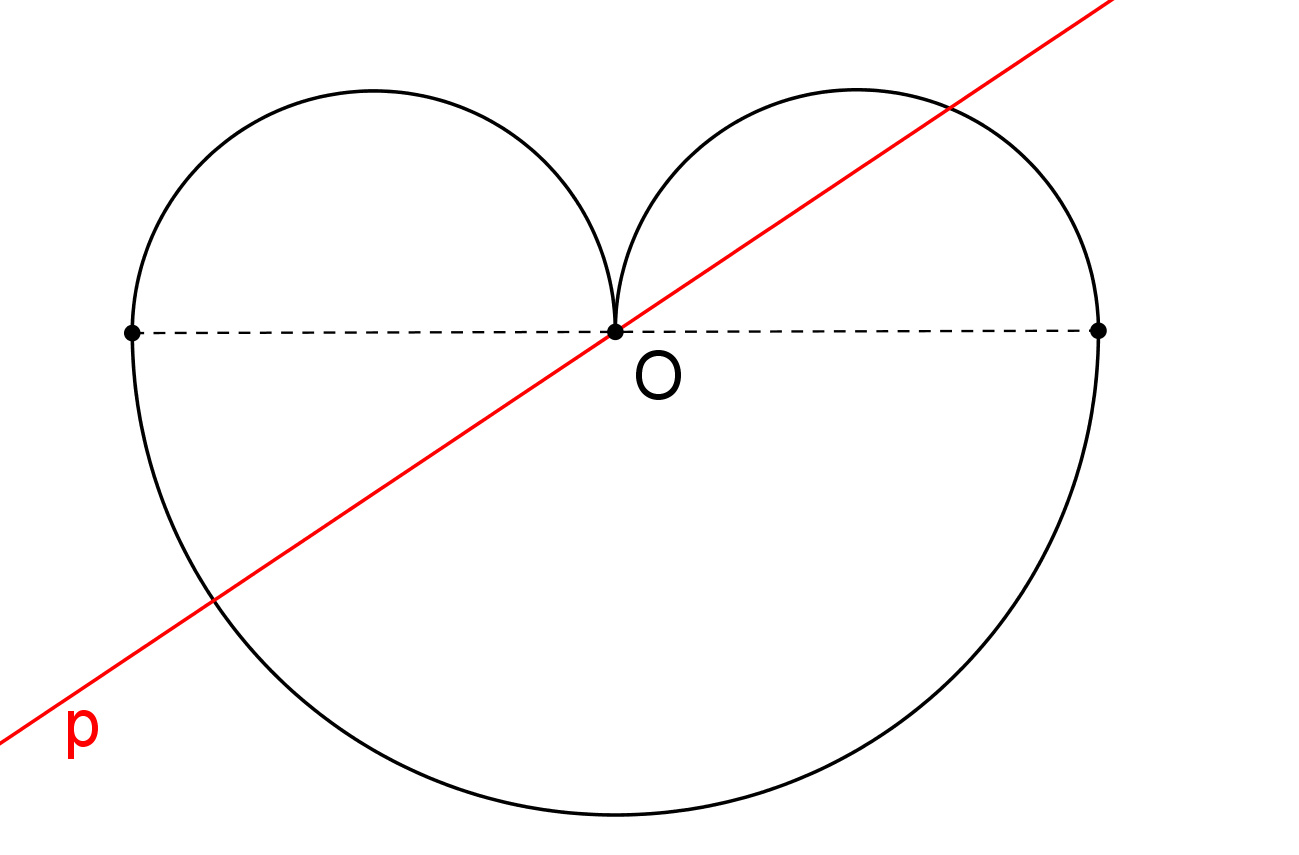
6. Jsou dány body P, Q a přímka l, přitom body P, Q leží v opačných polorovinách vzhledem k l. Najděte bod T na přímce l tak, aby absolutní hodnota rozdílu vzdáleností ||PT|-|TQ|| byla pro dané body P, Q maximální (tj. největší možná). (PLA-2017/PU7)

   

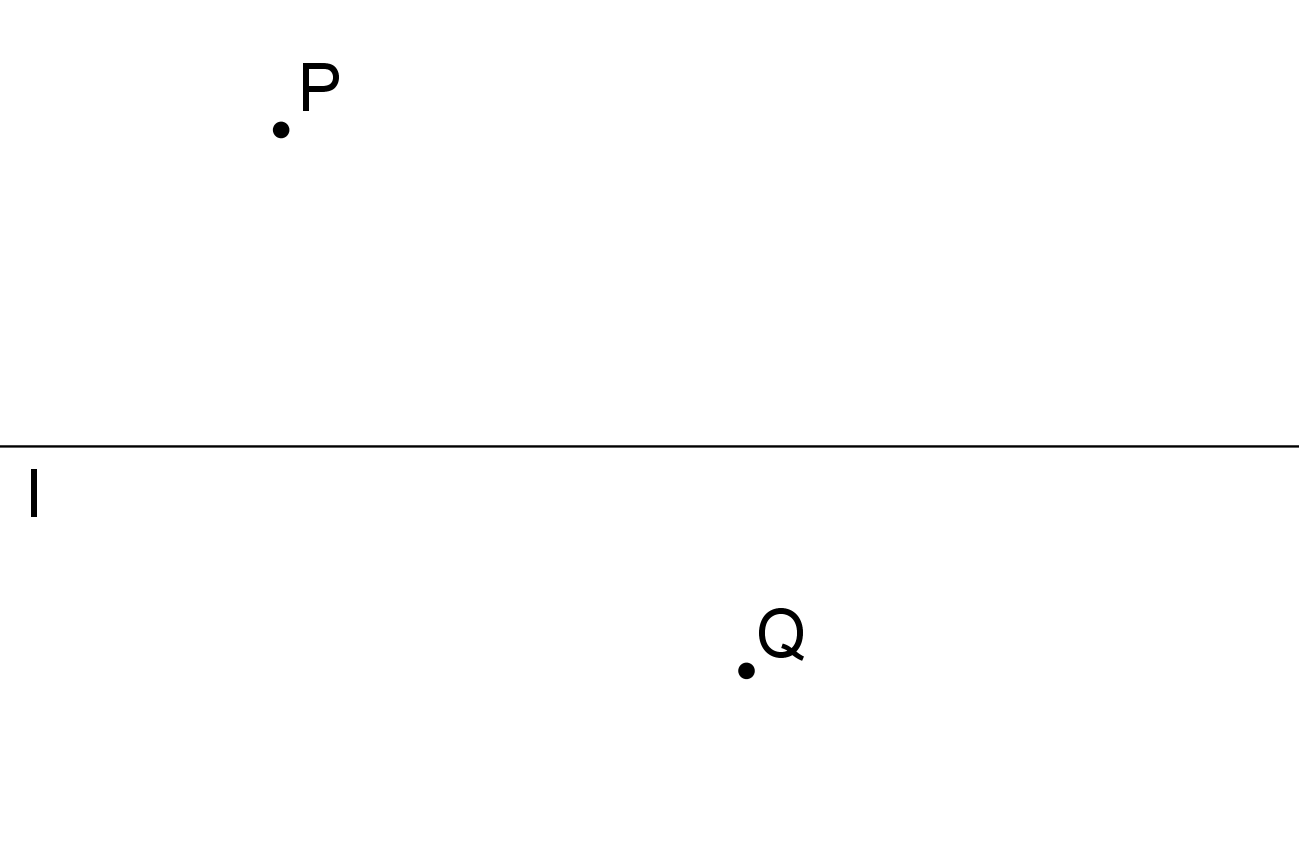
7. Libovolný trojúhelník je svými těžnicemi rozdělen na šest trojúhelníků se stejnými obsahy, viz obrázek. Dokažte! (PLA-2017/PU8)

   

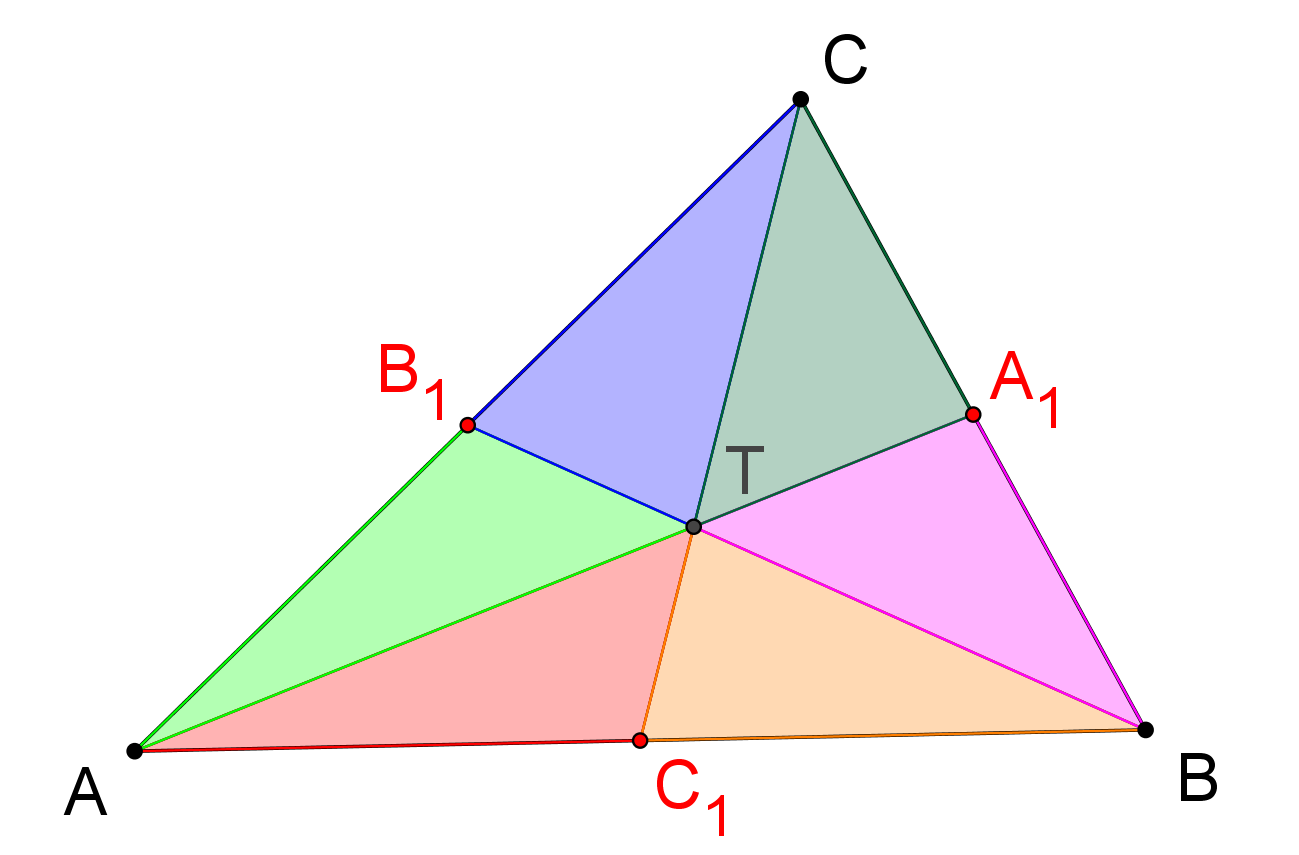
8. Nad stranami AC a BC trojúhelníku ABC jsou sestrojeny čtverce ACDE a BFGC, viz obrázek. Potom poloha středu M úsečky EF nezávisí na umístění vrcholu C (tj. bod M nemění při pohybu bodu C svou polohu). Dokažte! (PLA-2017/PU9)

   

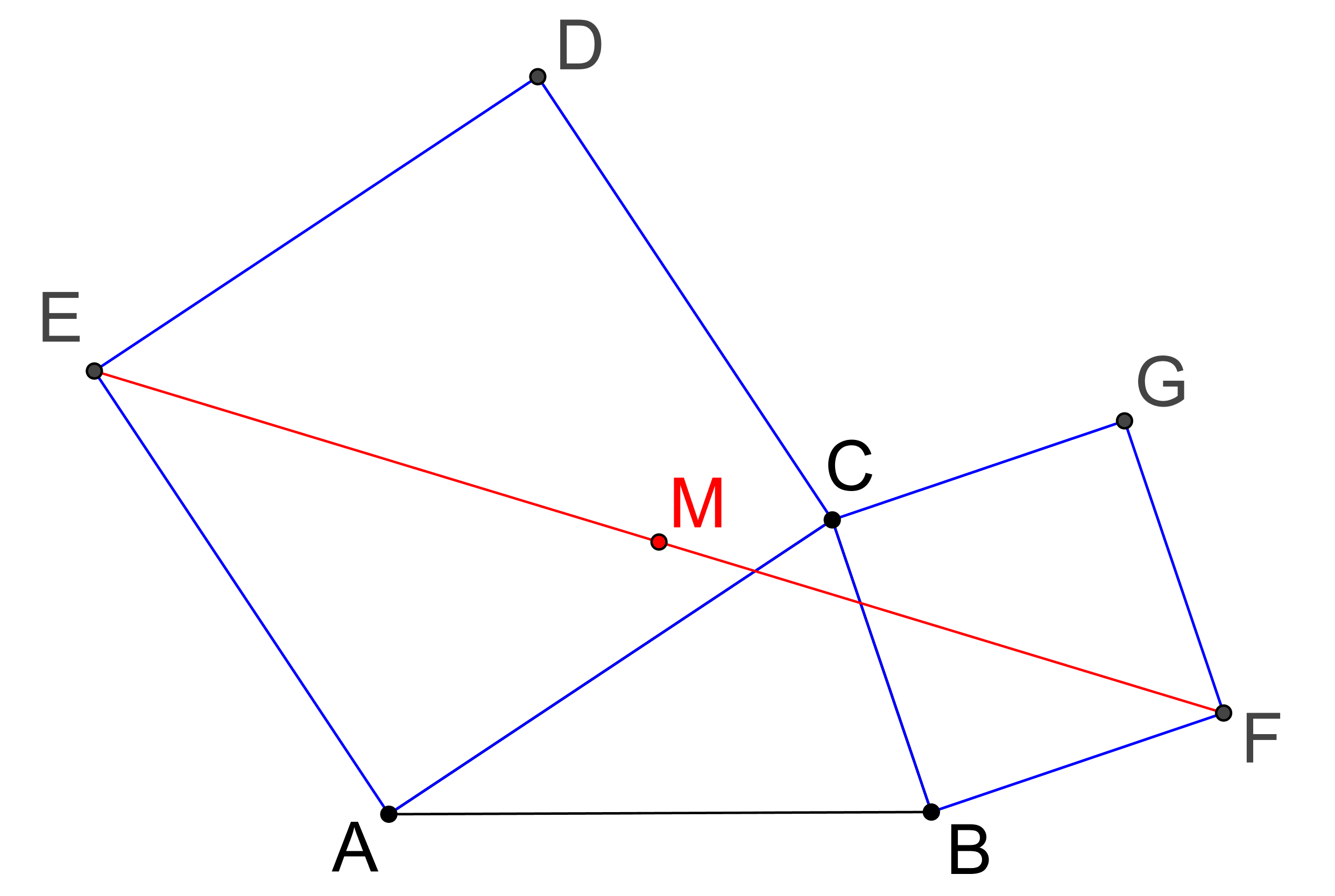
9. Jestliže jedna z úhlopříček dělí čtyřúhelník na dva trojúhelníky shodných obsahů, potom půlí druhou úhlopříčku. A naopak, pokud jedna z úhlopříček půlí druhou úhlopříčku, potom rozděluje čtyřúhelník na dva trojúhelníky shodných obsahů. Dokažte! (PLA-2017/PU10)

   

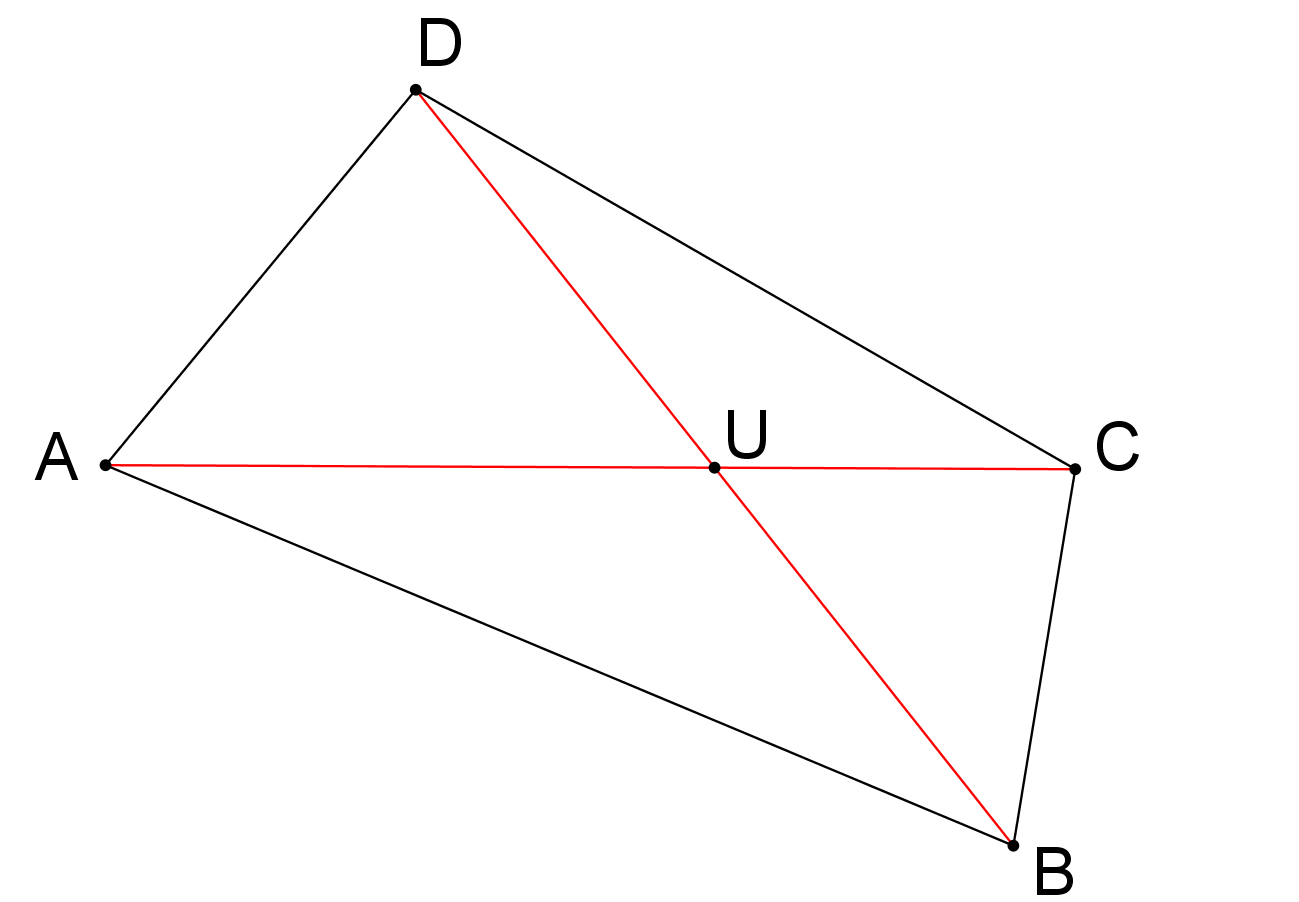
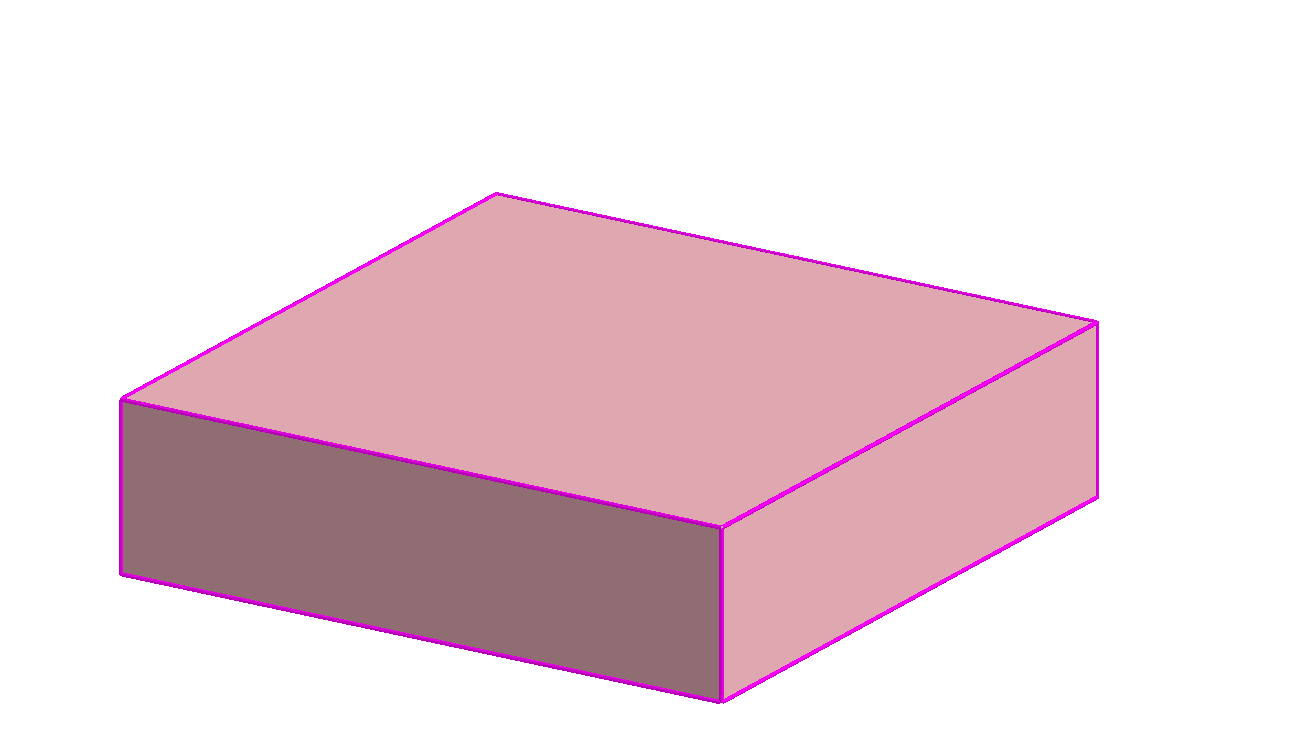
10. Dort ve tvaru kvádru s čtvercovým půdorysem je po stranách a nahoře pokryt marcipánovým potahem, viz obrázek. Navrhněte postup, jak tento dort rozdělit na 7 dílů téhož objemu tak, aby každý obsahoval stejné množství chutného potahu. (PLA-2017/PU11)

    

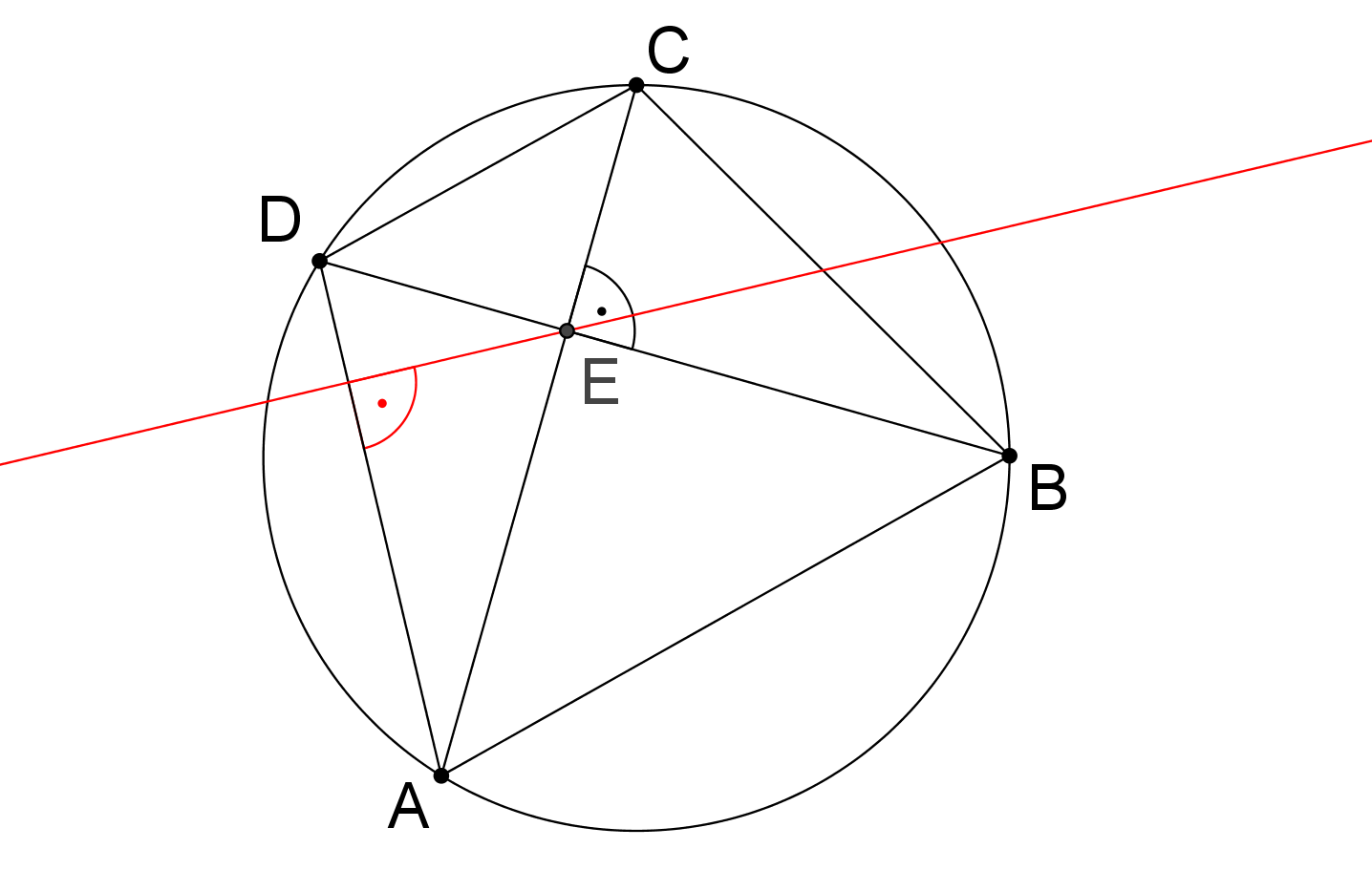
11. Jestliže má tětivový čtyřúhelník (tj. čtyřúhelník vepsaný do kružnice) vzájemně kolmé úhlopříčky, které se protínají v bodě E, přímka jdoucí bodem E kolmo k libovolné jeho straně půlí protilehlou stranu, viz obrázek. Dokažte! (PLA-2017/PU12)

    

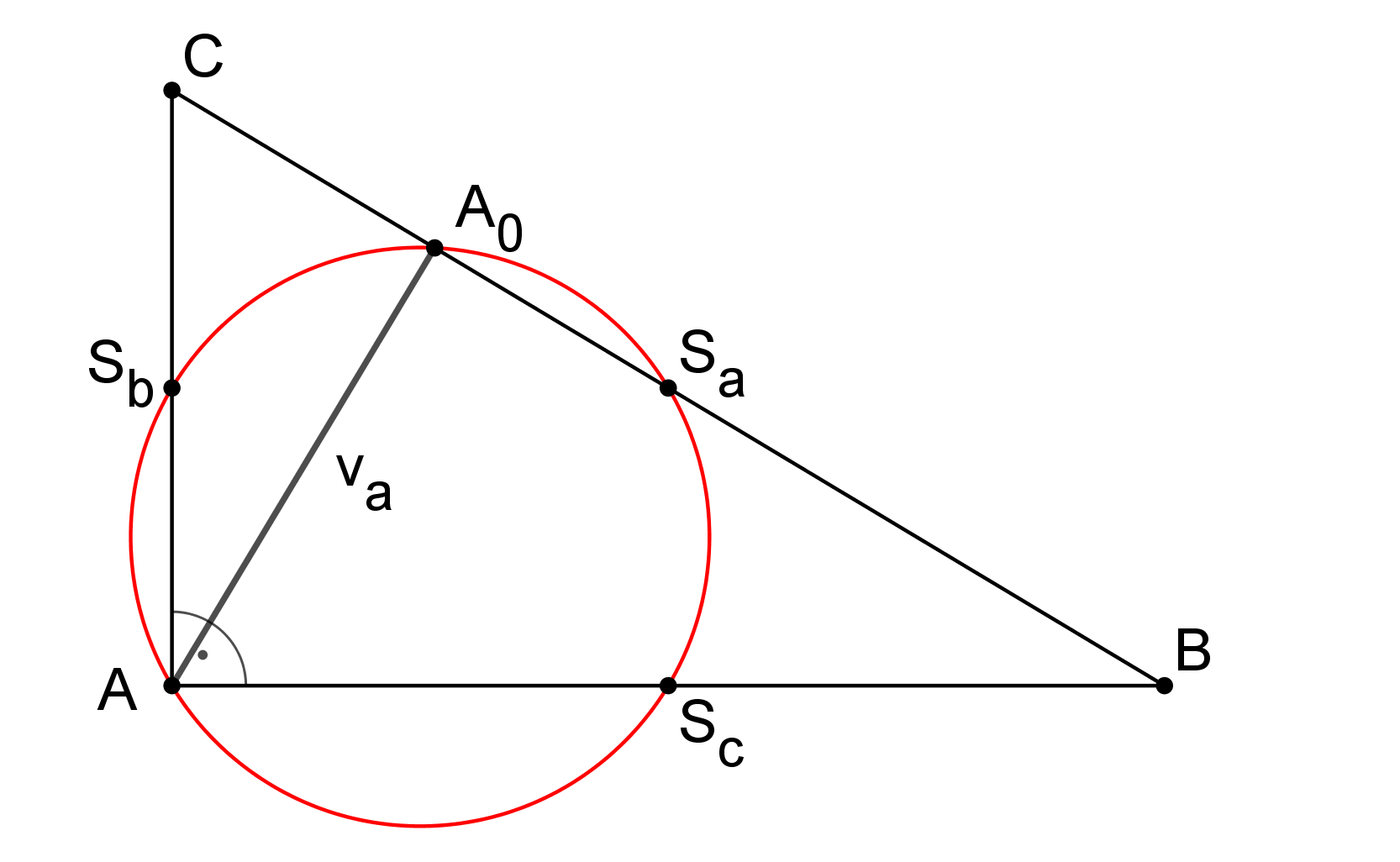
12. Nechť ABC je libovolný pravoúhlý trojúhelník s pravým úhlem při vrcholu A. Dokažte, že bod A, pata A₀ výšky sestrojené z bodu A a středy S_a, S_b a S_c stran trojúhelníku ABC leží na společné kružnici, viz obrázek. (PLA-2018/PU2)

    

13. Podle levého obrázku rozstřiháme čtverec o straně 8 cm na čtyři části, z nichž sestavíme obrazec ve tvaru obdélníku vpravo. Jeho rozměry jsou 13 cm × 5 cm. Porovnáme-li obsahy obou obrazců, čtverce a obdélníku, zjistíme, že se liší o 1 cm². Čtverec má obsah 64 cm², obdélník pak 65 cm². Jak mohl tento rozdíl vzniknout? Vysvětlete! (PLA-2018/PU3)

     

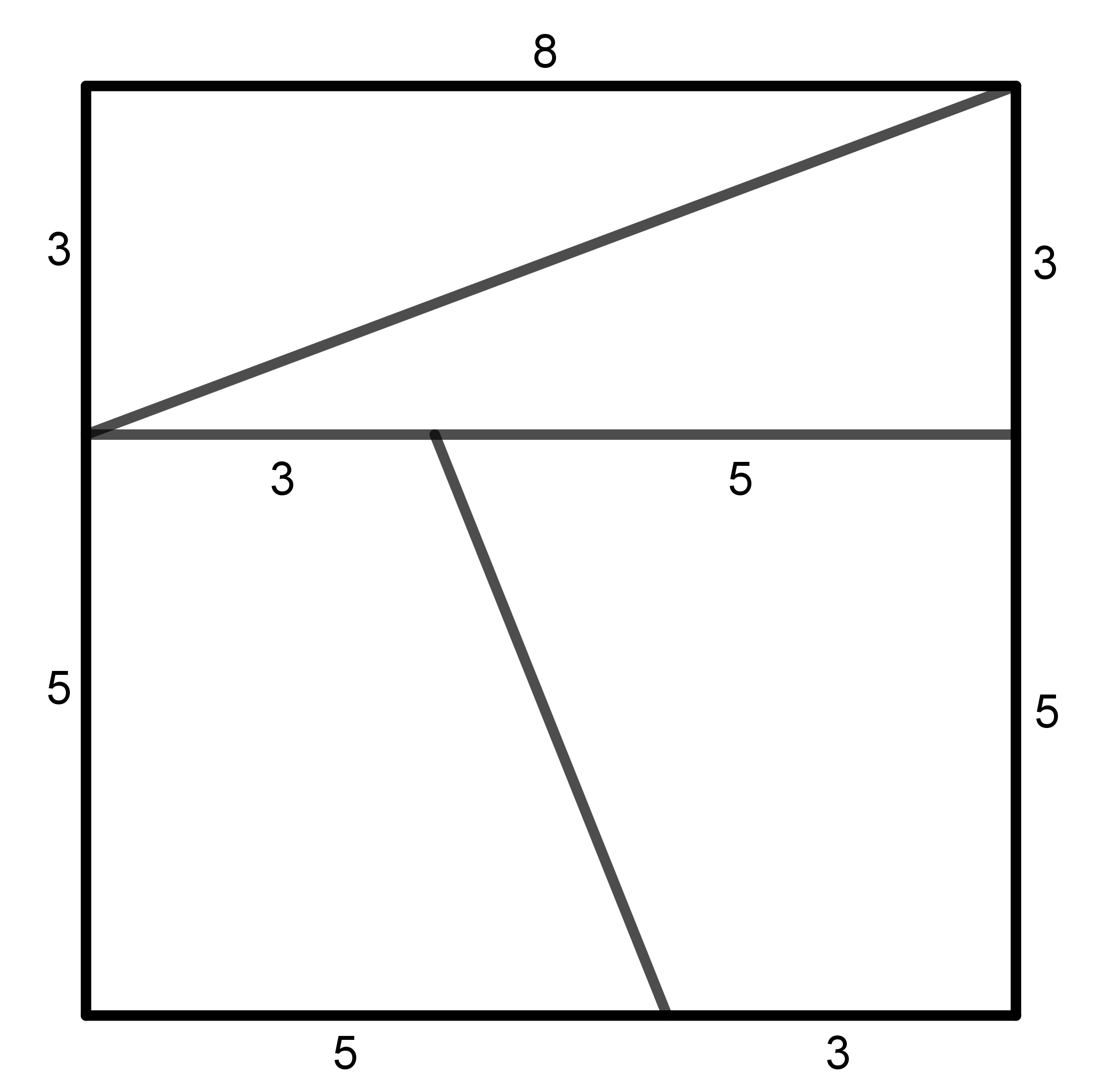
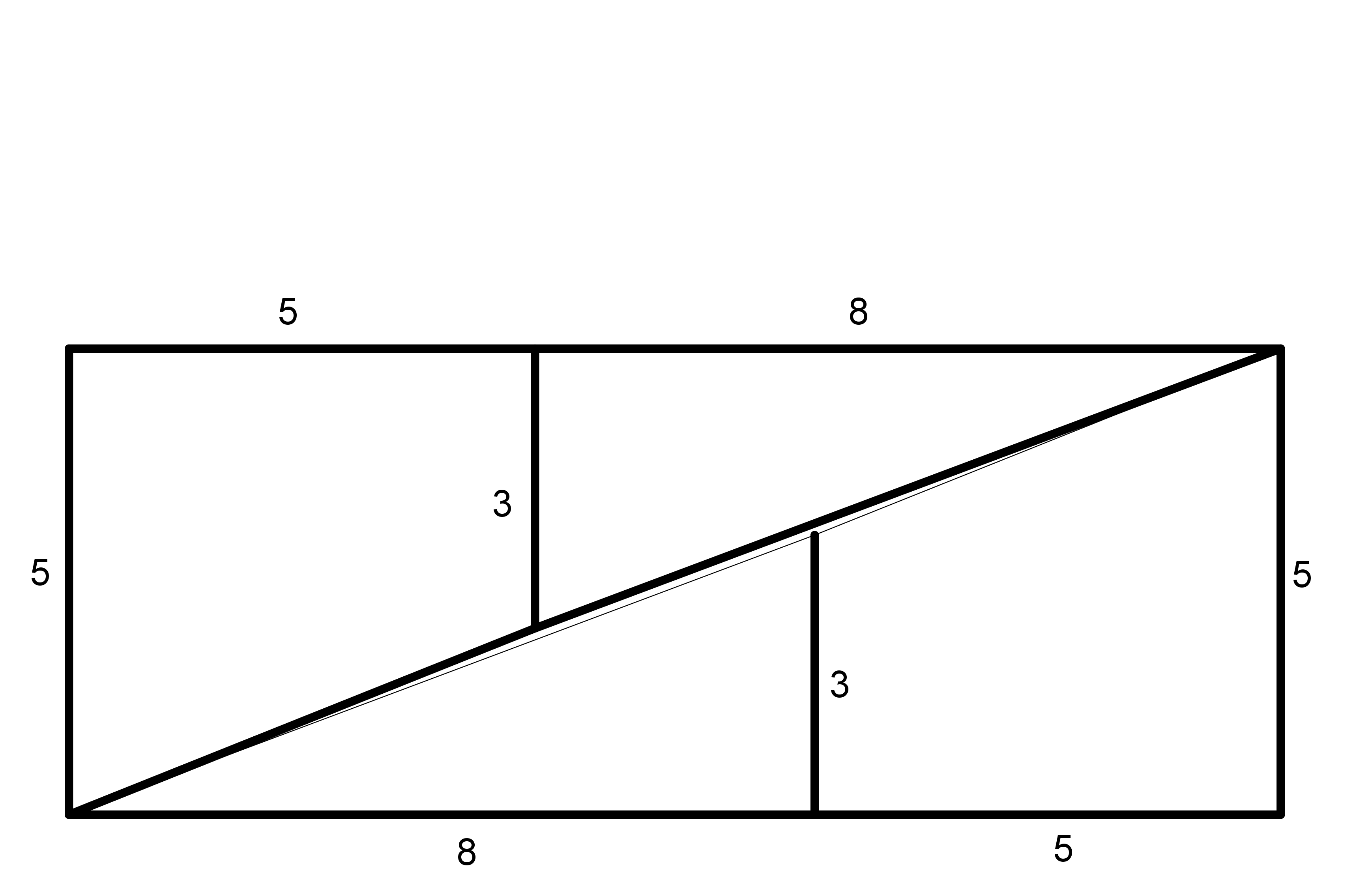
14. U libovolného trojúhelníku se stranami a, b, c označme k, l, m úsečky spojující vnější vrcholy čtverců sestrojených nad těmito stranami, viz obrázek. Dokažte, že platí

    k²+l²+m²=3(a²+b²+c²). (PLA-2018/PU4)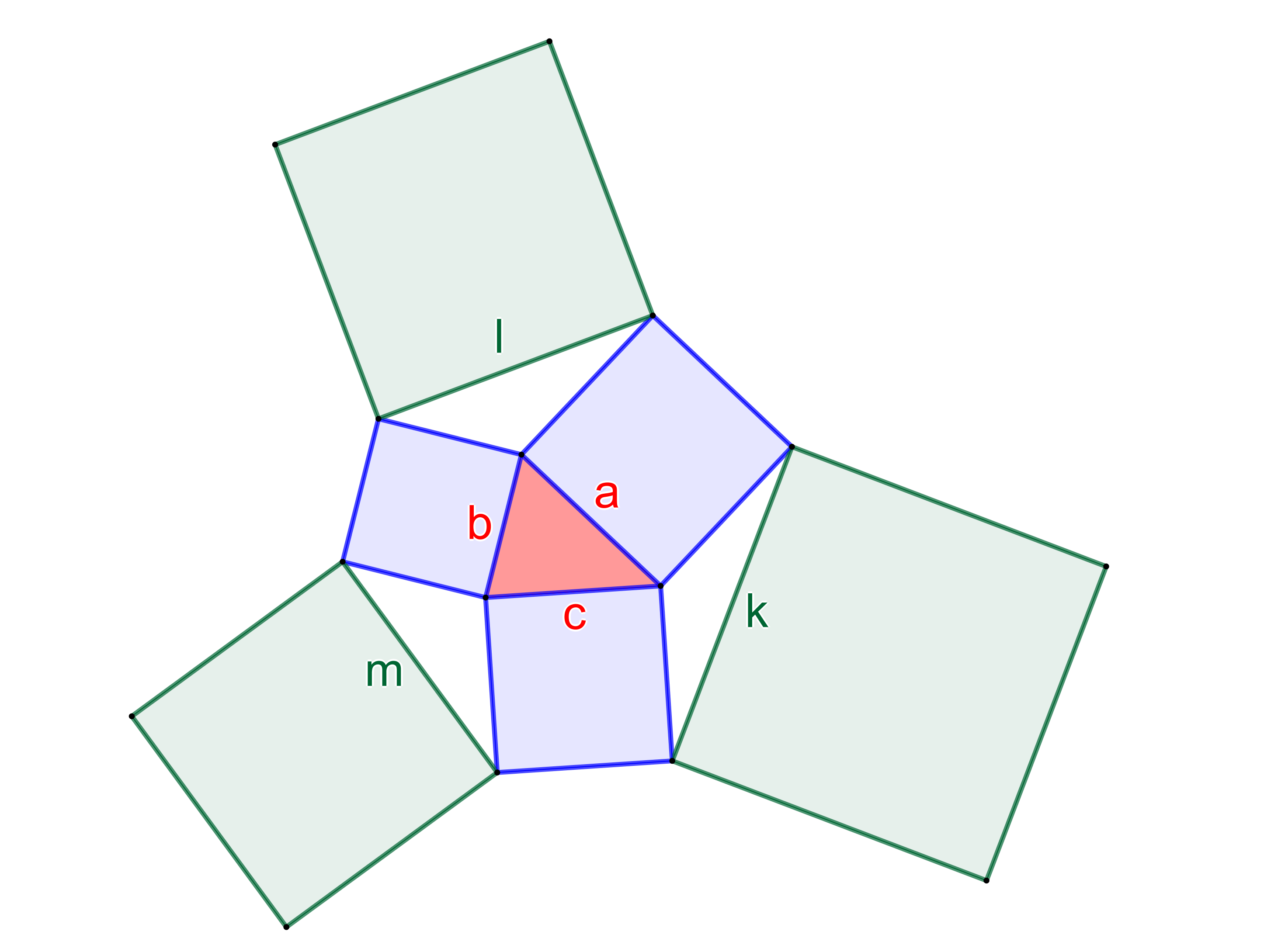

15. Tečnovým čtyřúhelníkem rozumíme čtyřúhelník, kterému lze vepsat kružnici (tj. jeho strany jsou tečnami této kružnice). Dokažte, že pro libovolný tečnový čtyřúhelník ABCD se stranami a, b, c, d, viz obrázek, platí

    a+c=b+d. (PLA-2018/PU5)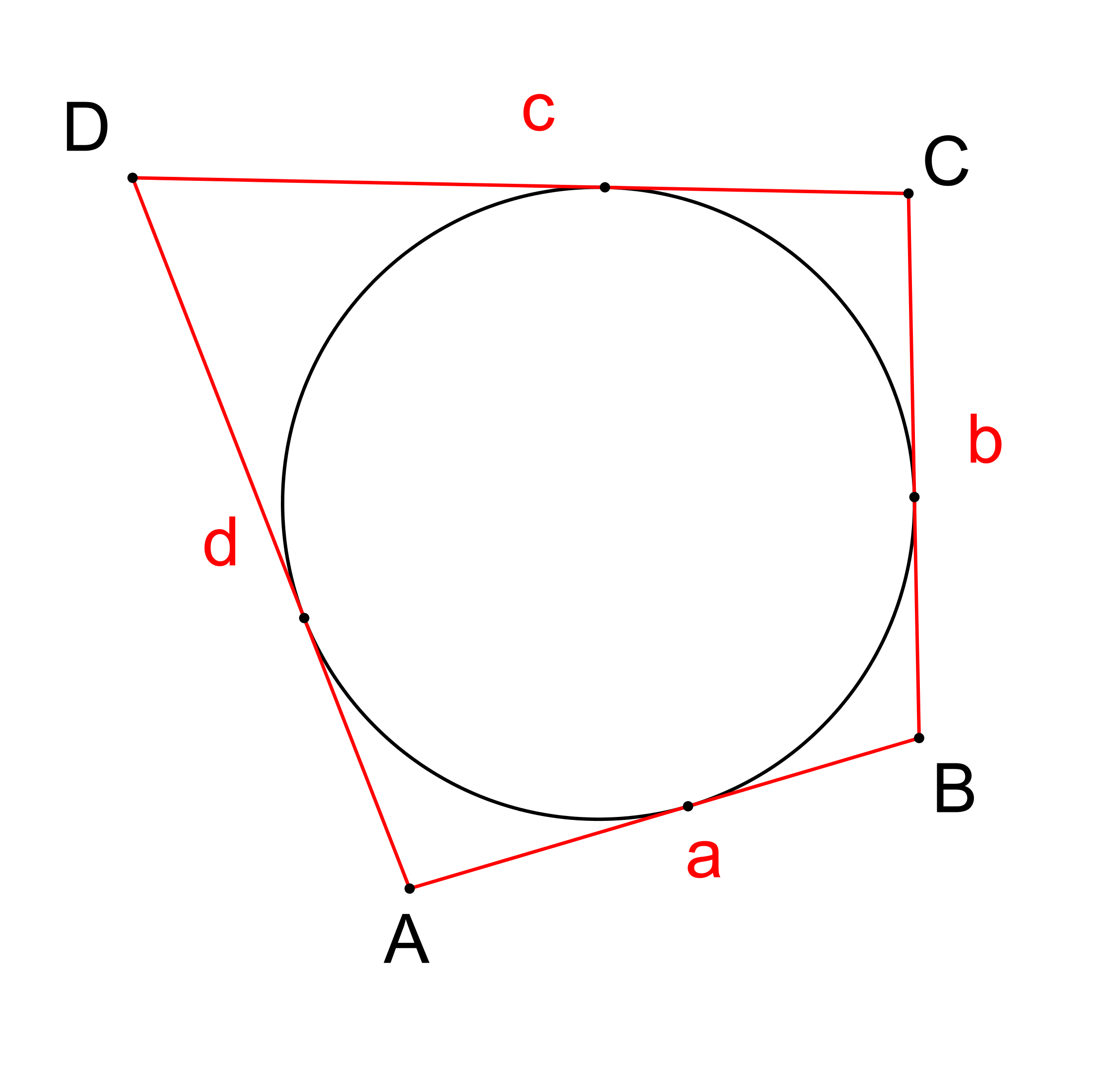

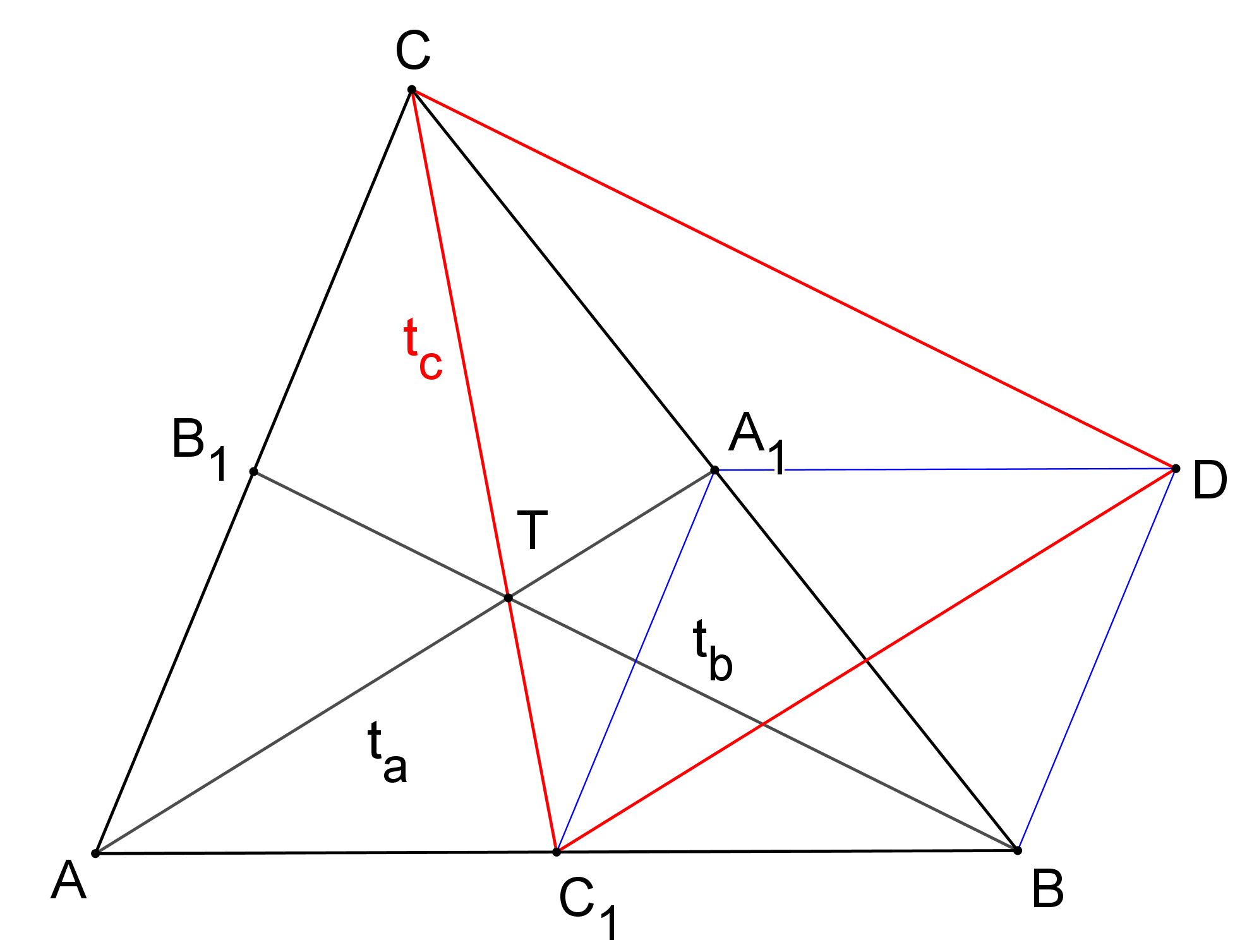
16. Dokažte, že pro libovolný trojúhelník je poměr jeho obsahu ku obsahu trojúhelníku sestrojeného z jeho těžnic roven 4:3, viz obrázek. (PLA-2018/PU6)

    

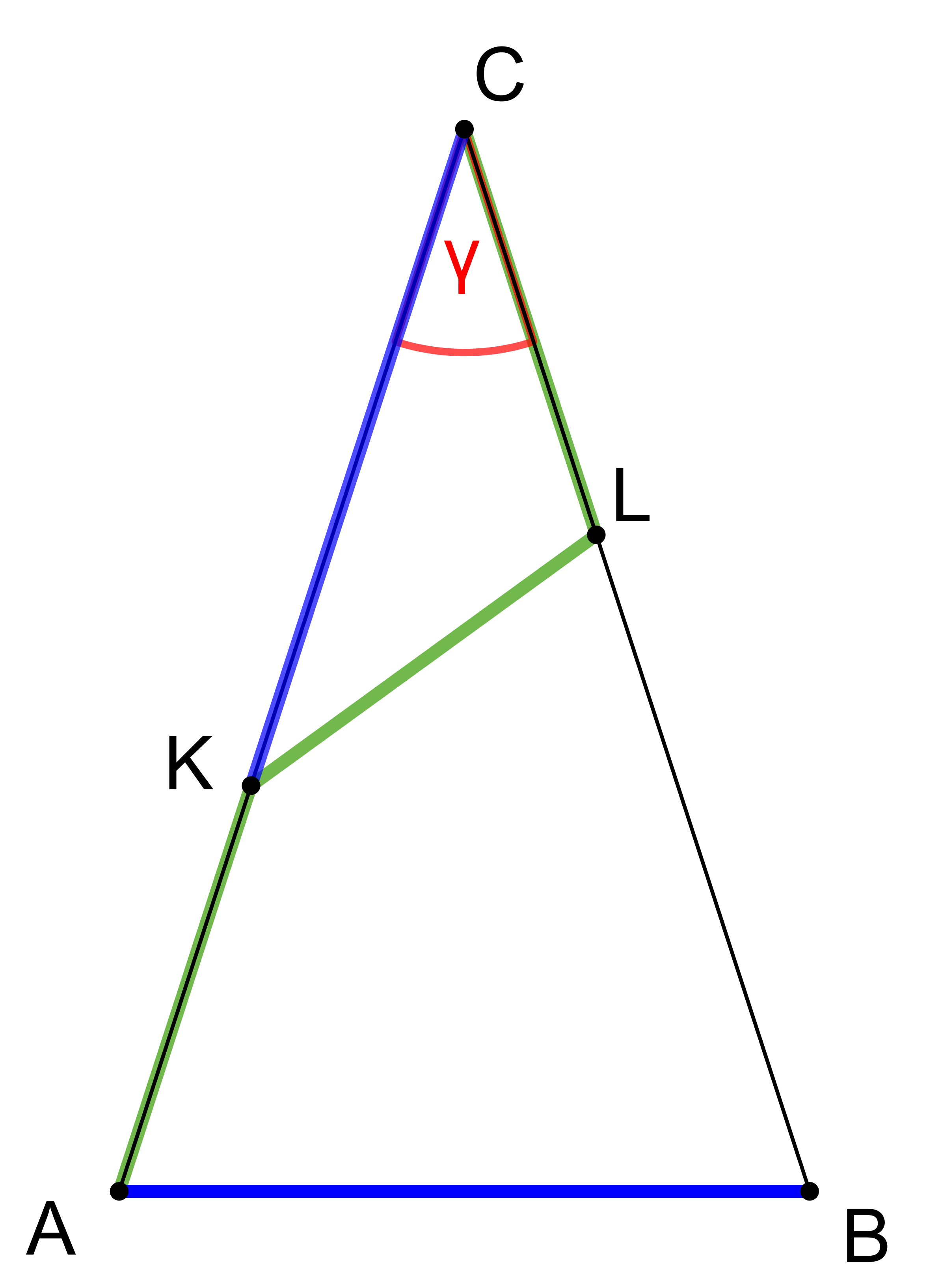
17. V rovnoramenném trojúhelníku ABC leží na ramenech AC a BC po řadě body K a L tak, že |AK|=|KL|=|LC| a |KC|=|AB|, viz obrázek. Určete velikost úhlu ACB. (PLA-2018/PU7)

    

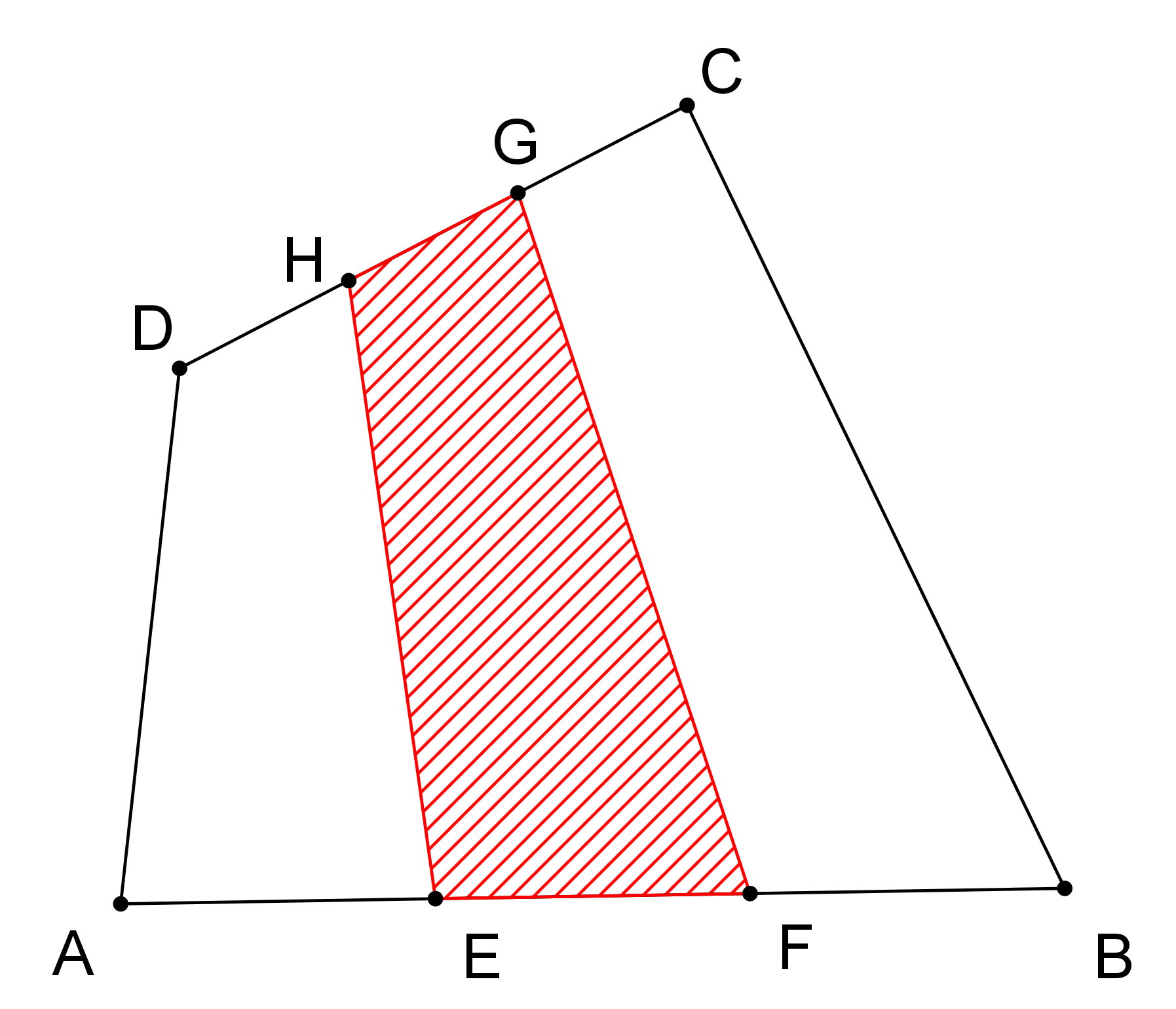
18. Jakou částí obsahu čtyřúhelníku ABCD je obsah čtyřúhelníku EFGH, viz obrázek, jestliže |AE|=|EF|=|FB| a |DH|=|HG|=|GC|? Své tvrzení dokažte! (PLA-2018/PU8)

    

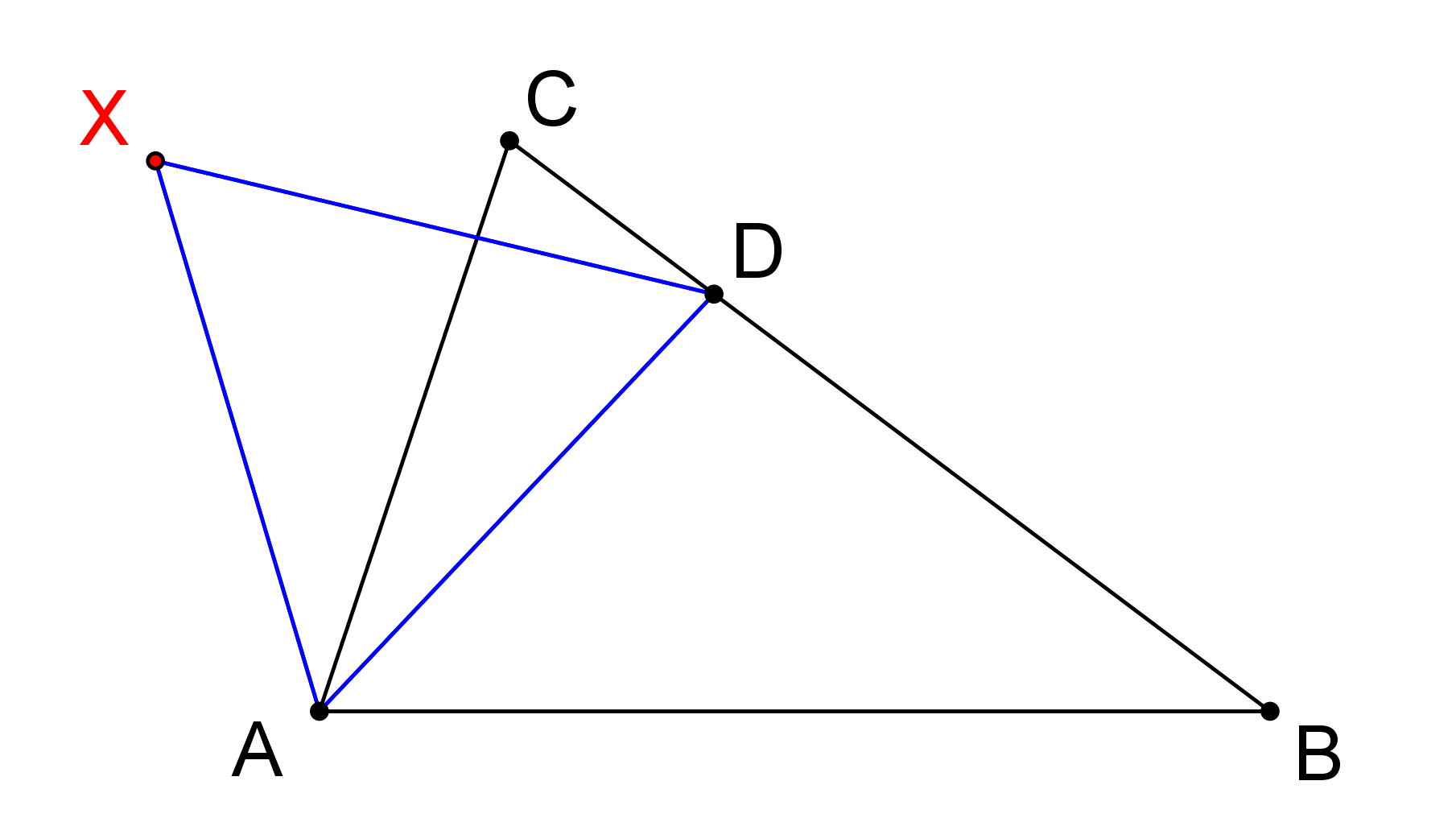
19. Pro daný trojúhelník ABC určete množinu bodů X, pro které existuje bod D na BC tak, že trojúhelník ADX je rovnostranný, viz obrázek. (PLA-2018/PU9)

    

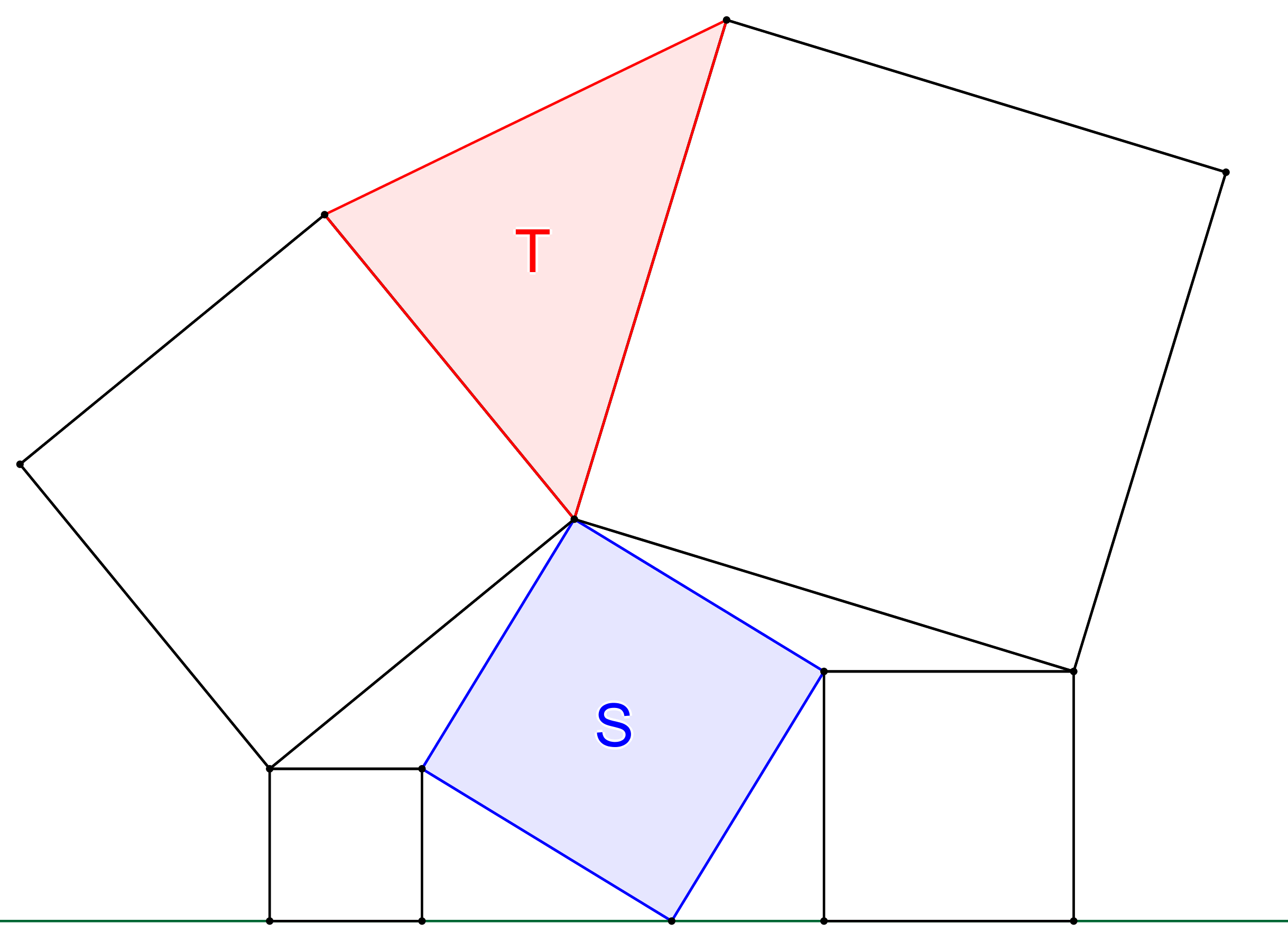
20. Pět čtverců je uspořádáno jako na obrázku. Dokažte, že obsah (modrého) čtverce S je roven obsahu (červeného) trojúhelníku T. (PLA-2018/PU10)

    

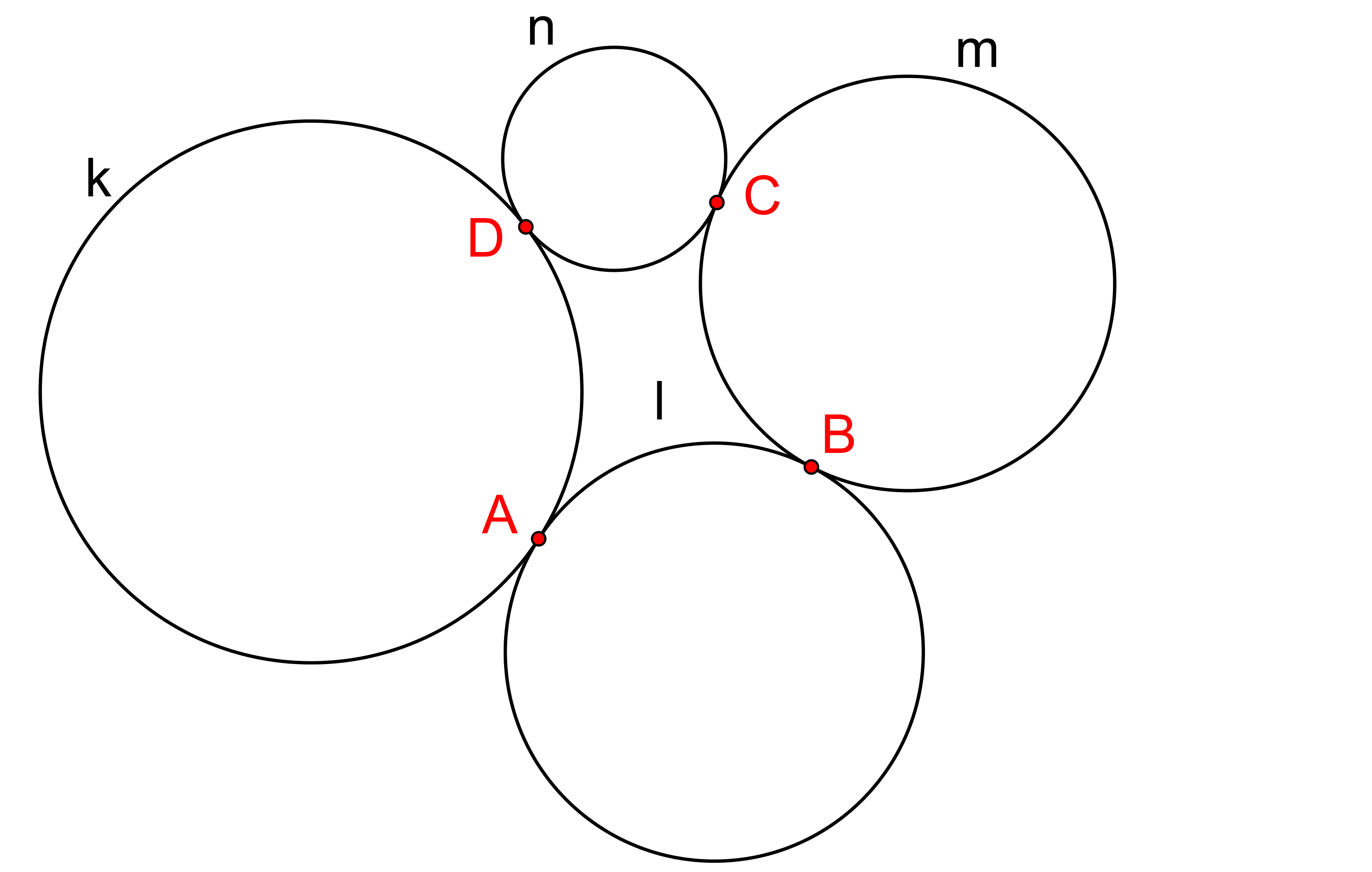
21. Čtyři kružnice k, l, m, n jsou uspořádány do uzavřeného řetězu, v němž mají každé dvě sousední kružnice vždy jeden společný bod, viz obrázek. Dokažte, že tyto body dotyku A, B, C, D leží (pro každé takové uspořádání čtyř kružnic) na společné kružnici. (PLA-2018/PU11)

    

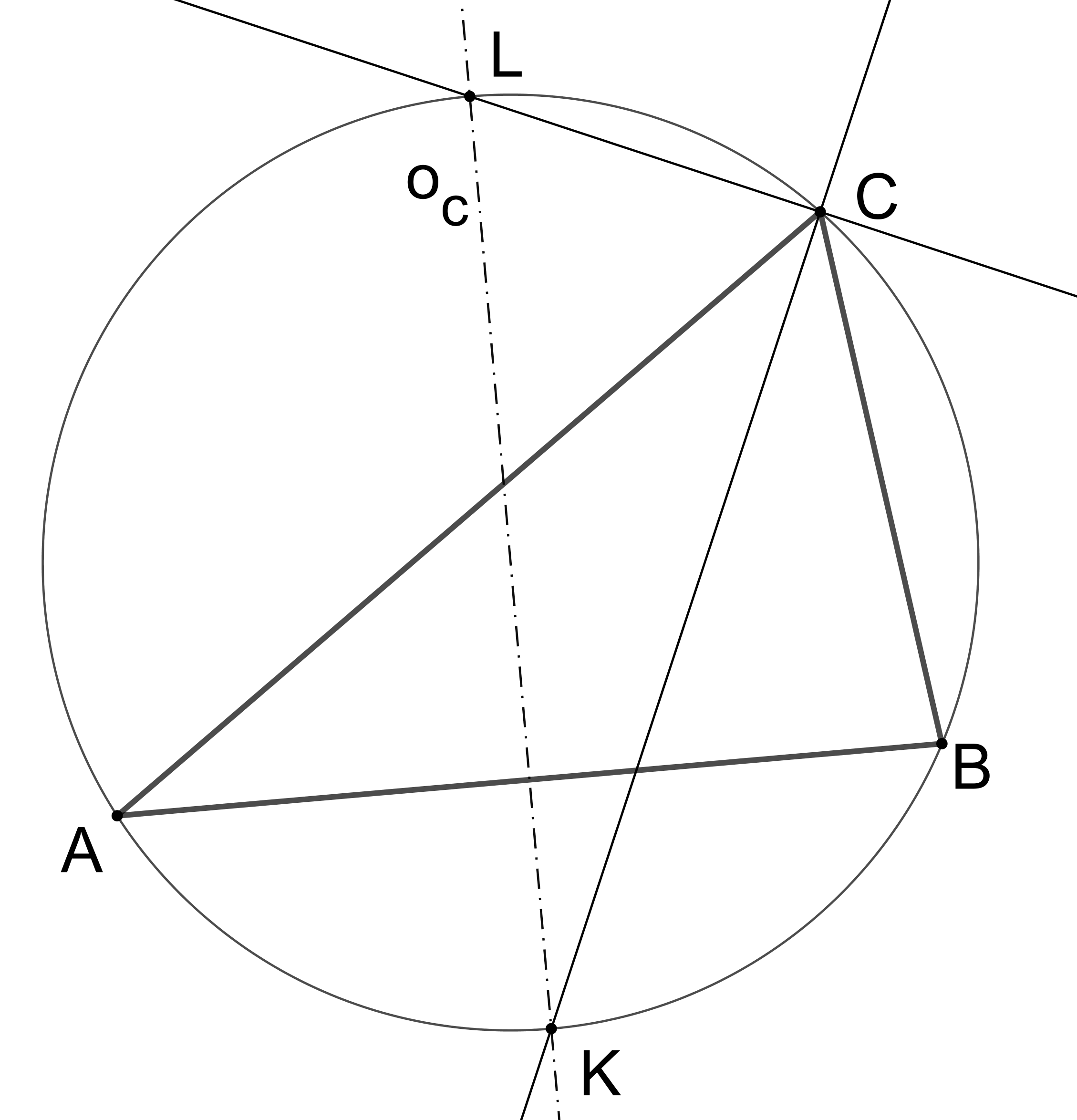
22. Pro libovolný trojúhelník ABC protíná osa O_c jeho strany AB kružnici trojúhelníku opsanou v bodech K a L, viz obrázek. Dokažte, že přímka CK je osou vnitřního úhlu tohoto trojúhelníku při vrcholu C, zatímco přímka CL je osou vnějšího úhlu trojúhelníku při vrcholu C. (PLA-2019/PU1)

    

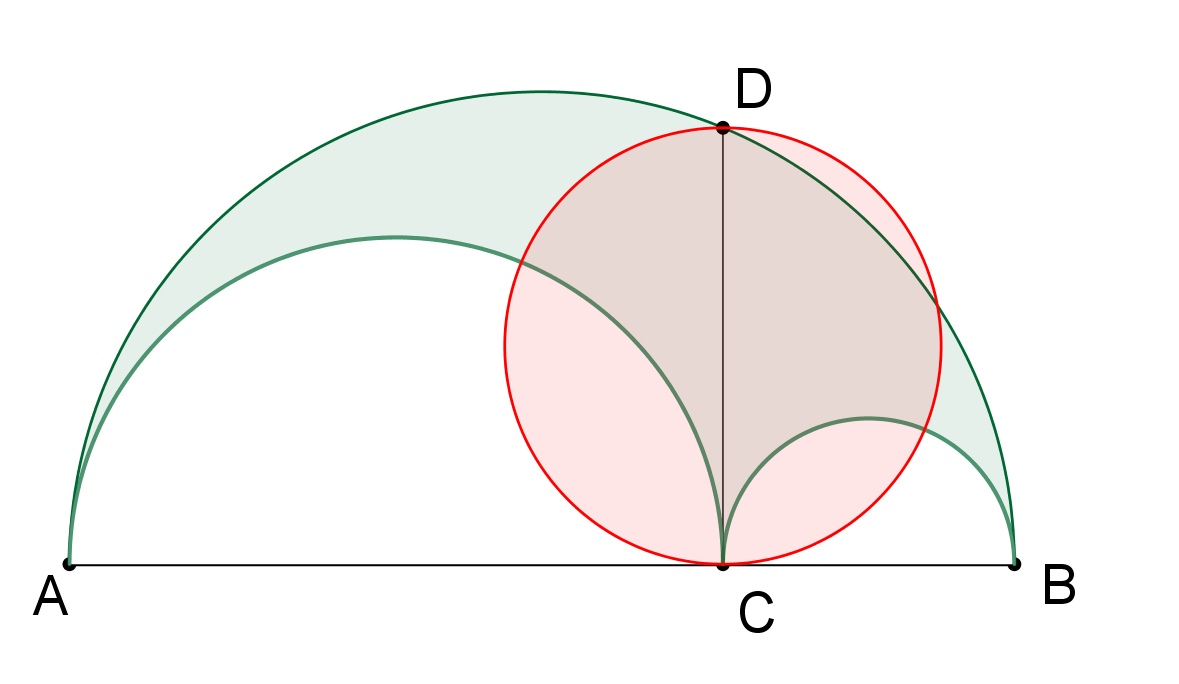
23. Do půlkruhu s průměrem AB jsou vepsány půlkruhy s průměry AC a CB, z bodu C je potom vedena kolmice protínající hraniční půlkružnici v bodě D, viz obrázek. Dokažte, že obsah zelené plochy v obrázku je roven obsahu červeného kruhu s průmerem CD. (PLA-2019/PU2)

    

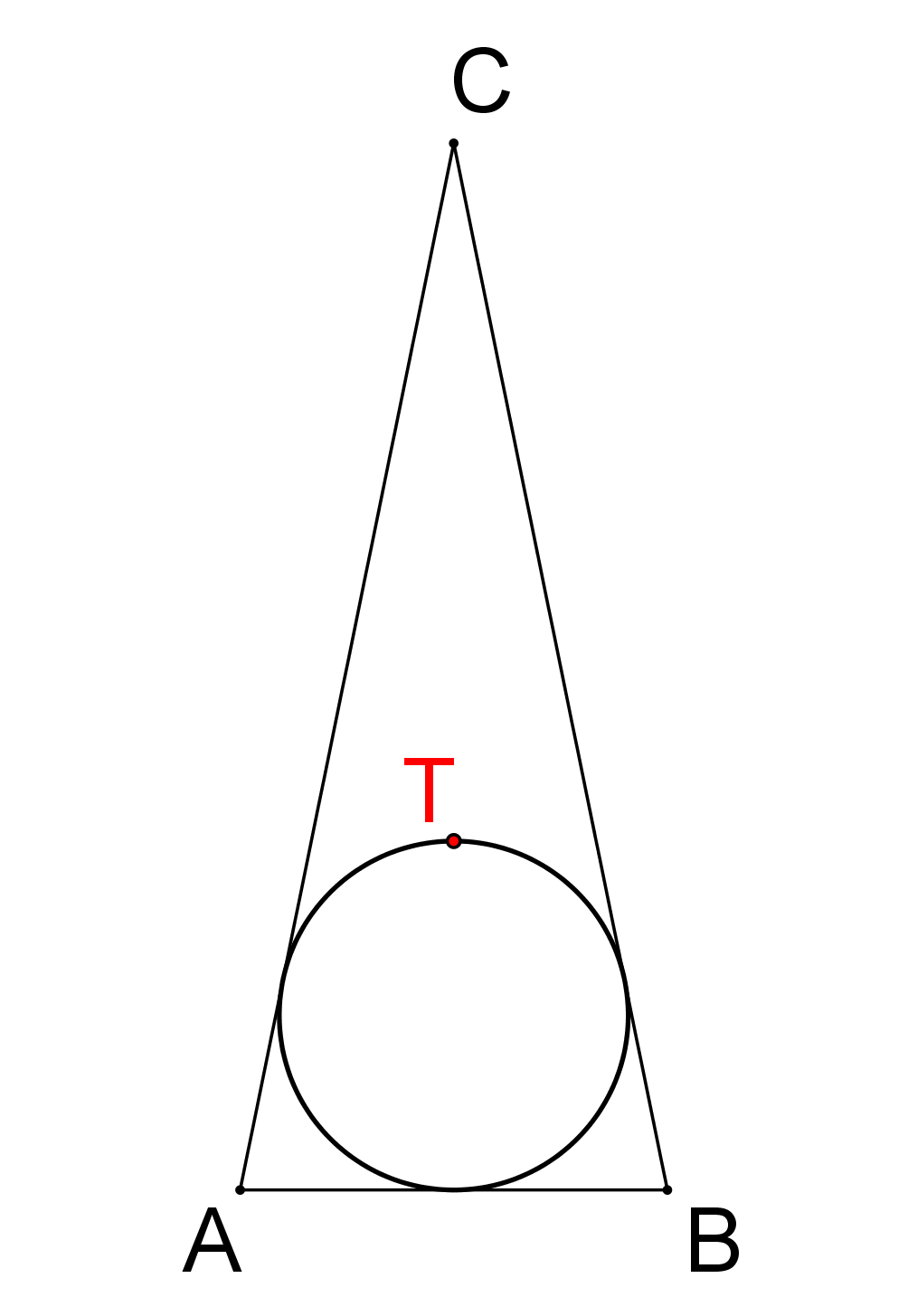
24. Kružnice vepsaná rovnoramennému trojúhelníku ABC prochází jeho těžištěm T, viz obrázek. Dokažte, že AC/AB = 5/2. (PLA-2019/PU3)

    

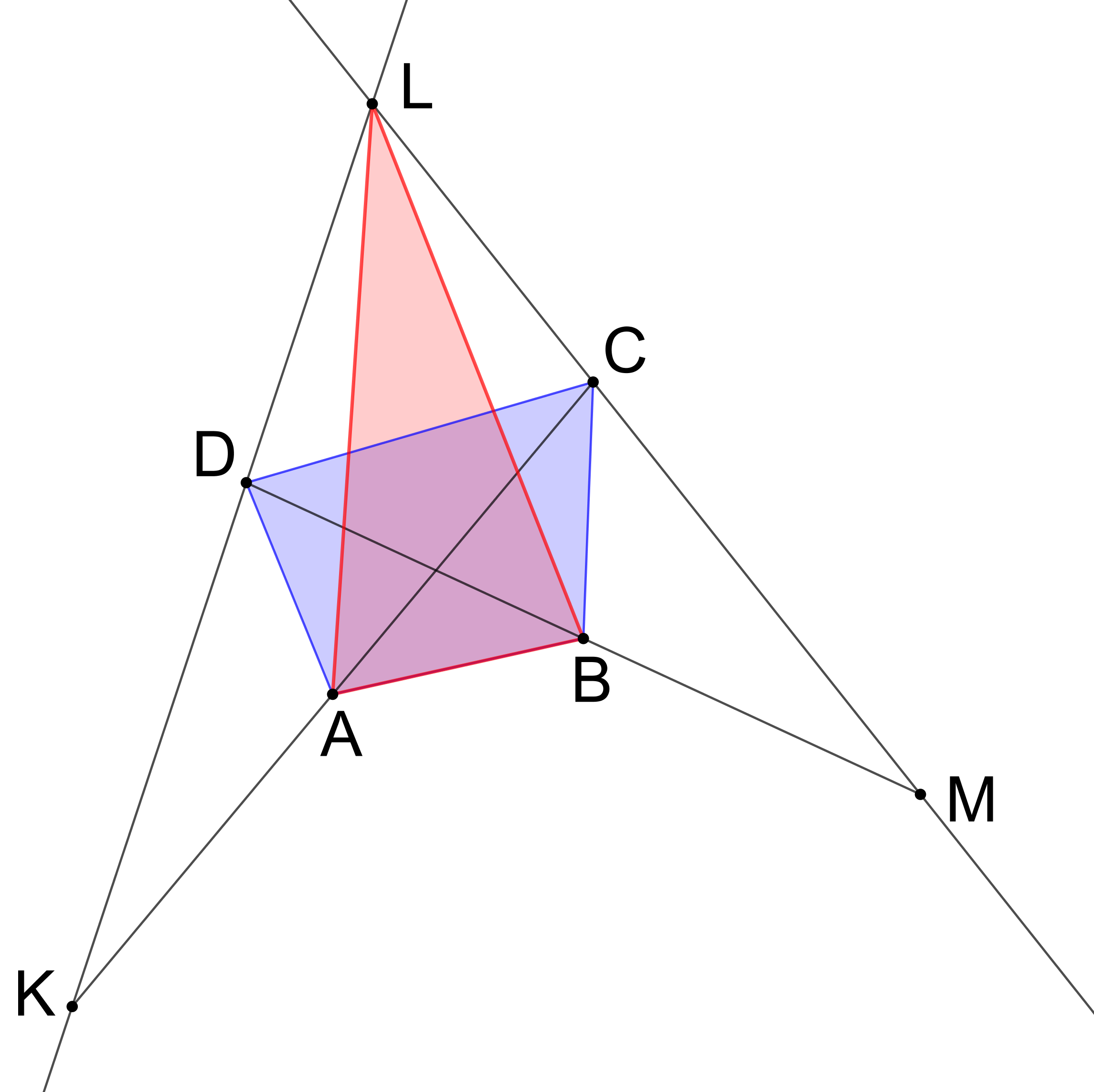
25. Jsou dány různoběžné přímky KL, LM se společným bodem L, viz obrázek. Body C a D potom leží v daném pořadí libovolně na úsečkách LM a KL a body A a B jsou v uvedeném pořadí středy úseček KC a MD. Dokažte, že čtyřúhelník ABCD má stejný obsah jako trojúhelník ABL. (PLA-2019/PU4)

    
    
    [Dynamický obrázek v GeoGebře]

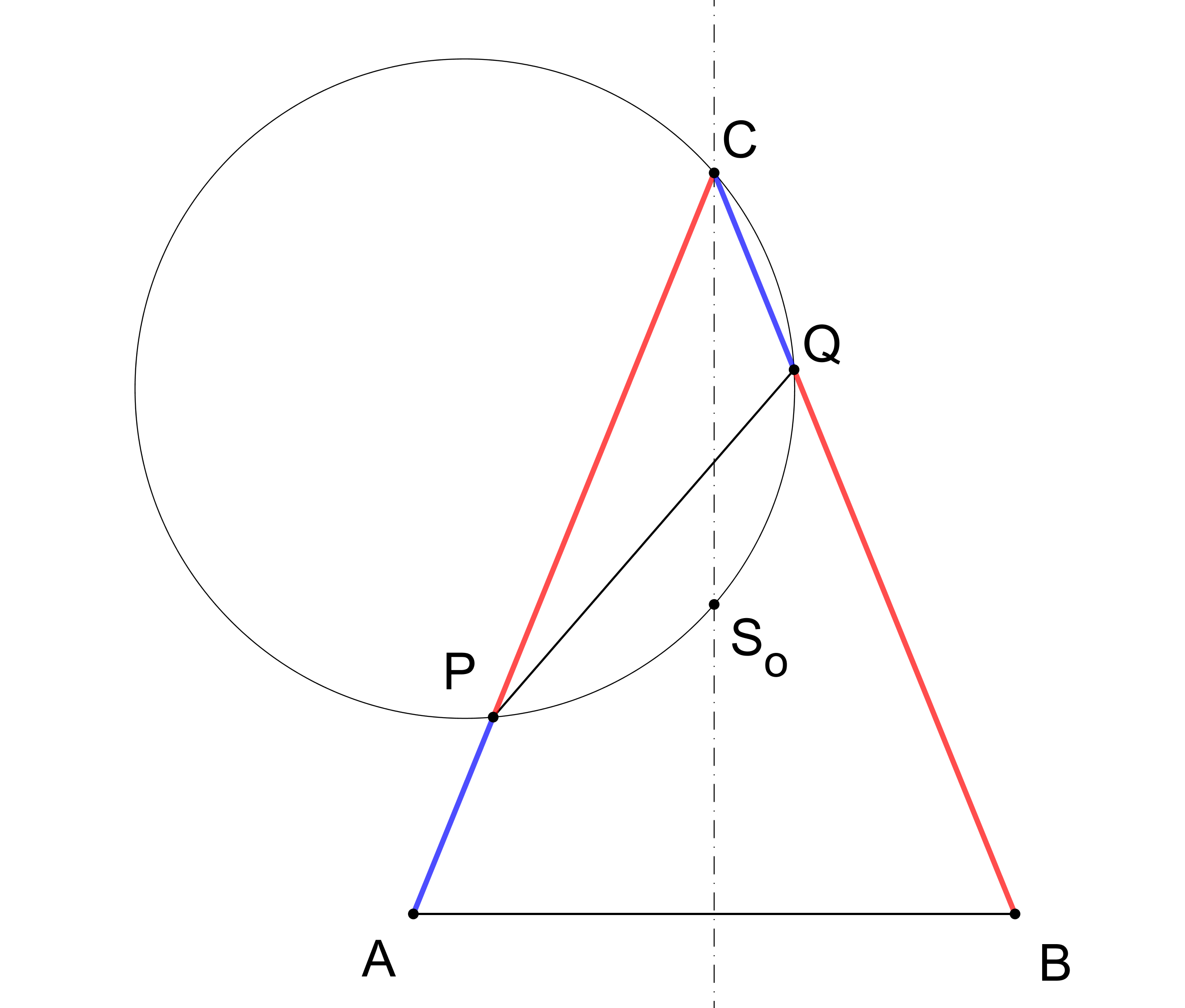
26. Na ramenech rovnoramenného trojúhelníku ABC jsou dány body P, Q, různé od vrcholů trojúhelníku, tak, že |PC|=|QB|, viz obrázek. Dokažte, že kružnice opsaná trojúhelníku PQC prochází středem S_o kružnice opsané trojúhelníku ABC. (PLA-2019/PU5)

    
    
    [Dynamický obrázek v GeoGebře]

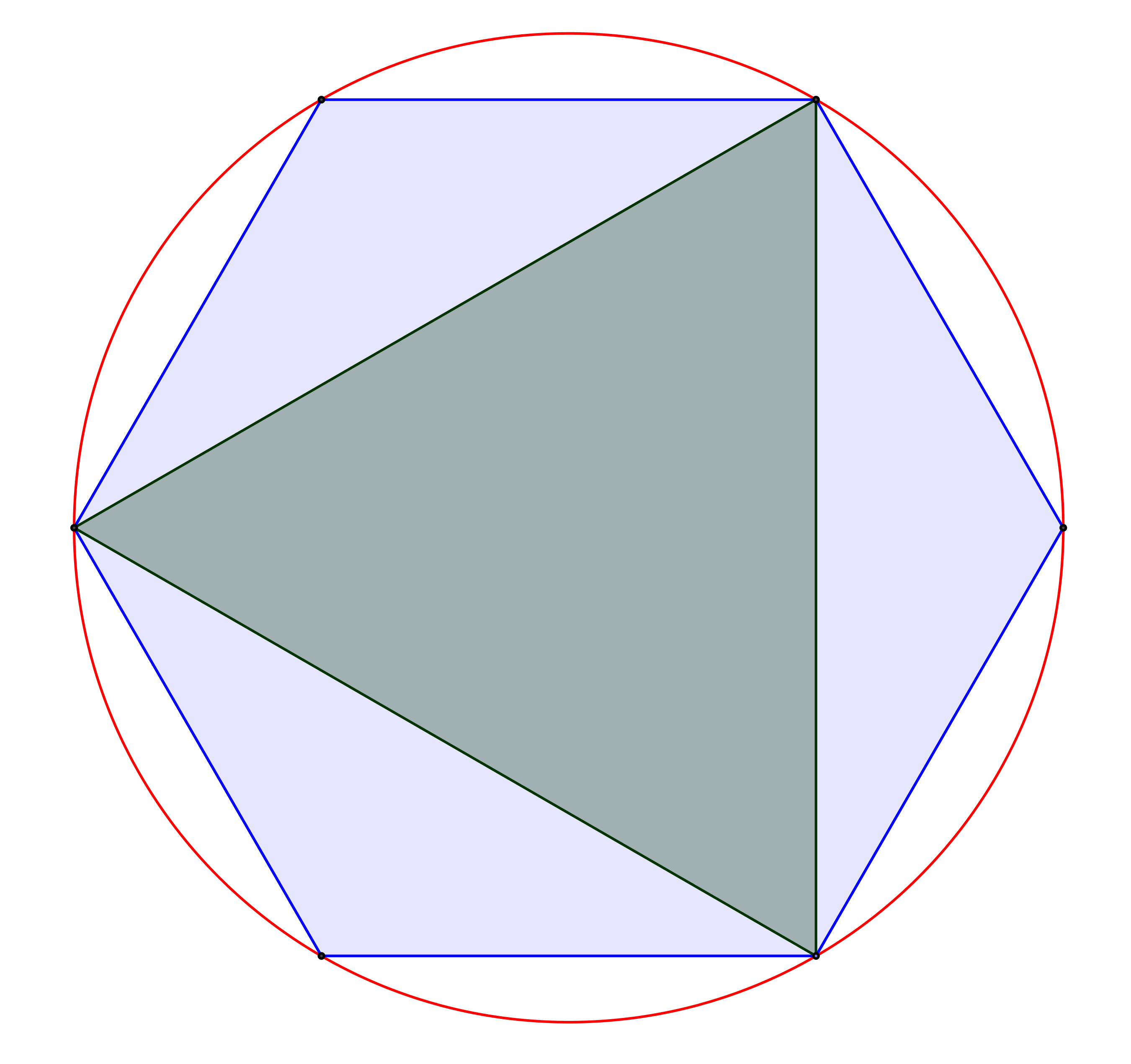
27. Do kružnice je vepsán rovnostranný trojúhelník spolu s pravidelným šestiúhelníkem, s kterým má společné vrcholy, viz obrázek. Jaký je poměr jejich obsahů? Své tvrzení dokažte! (PLA-2019/PU6)

    

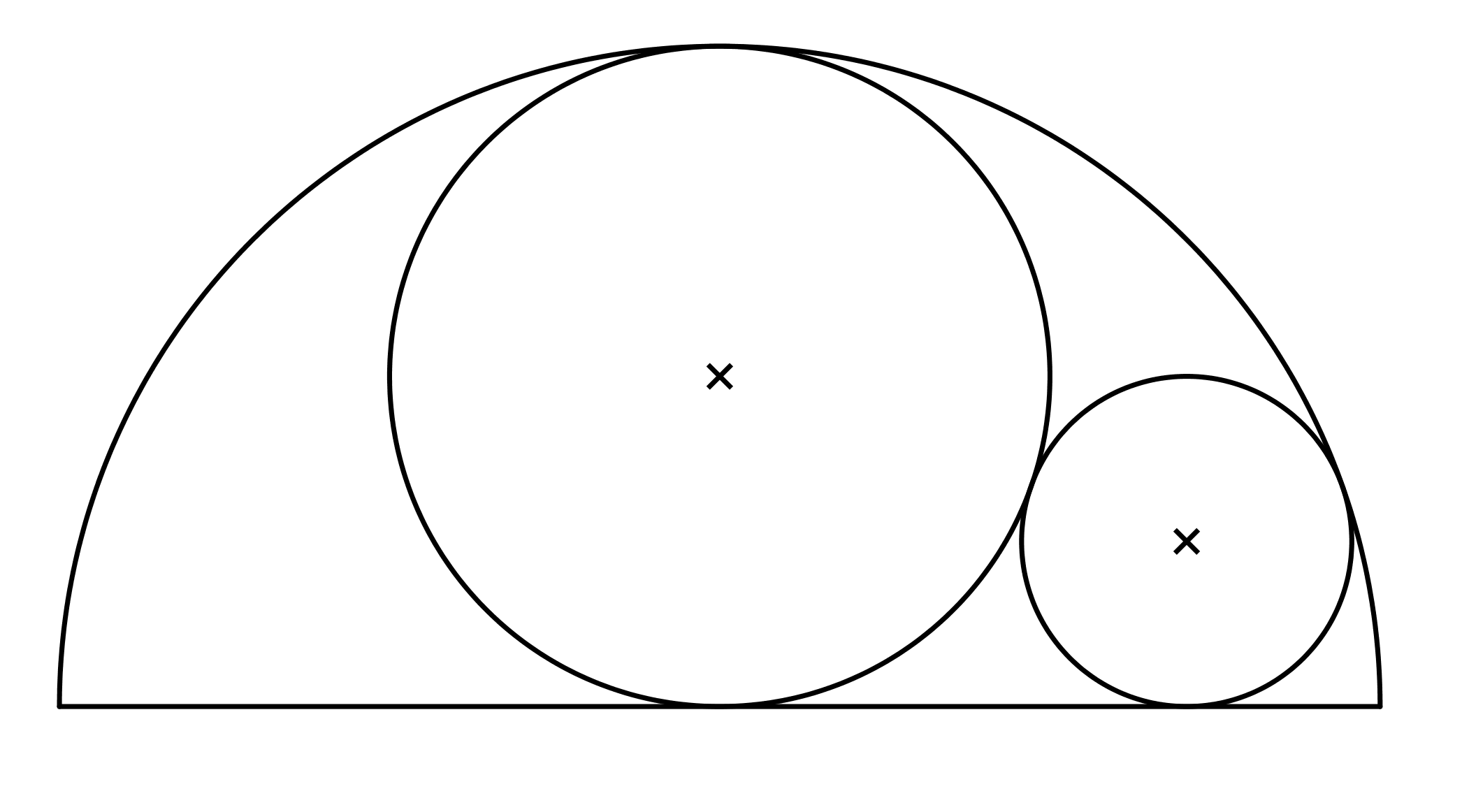
28. Do půlkruhu s poloměrem 4 jsou vepsány dva kruhy s průměry 4 a d, které se dotýkají, viz obrázek. Vypočtěte d. (PLA-2019/PU7)

    

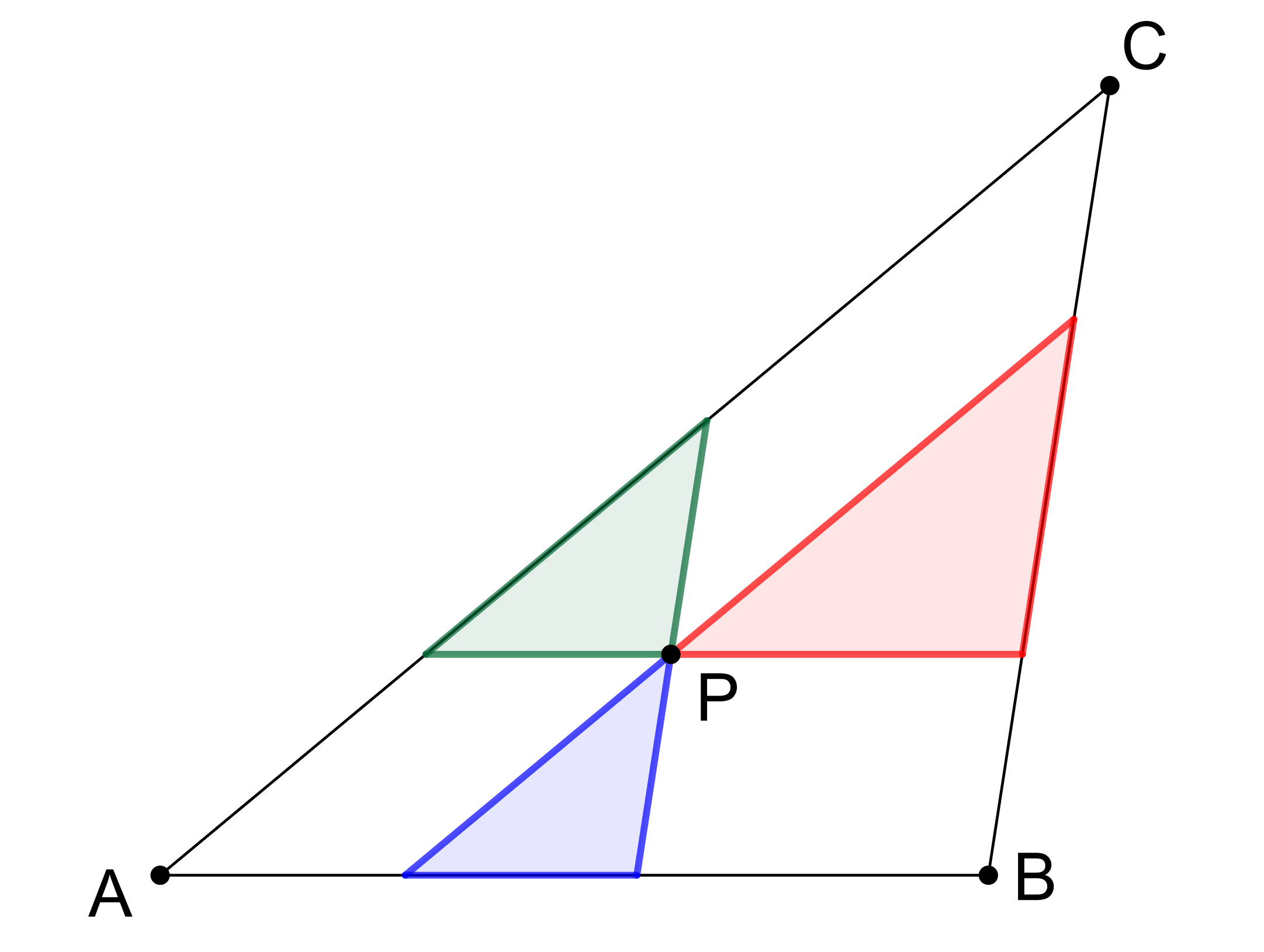
29. Uvnitř trojúhelníku ABC je dán bod P. Vedeme-li bodem P rovnoběžky se stranami daného trojúhelníku, dostaneme tři trojúhelníky a tři rovnoběžky, viz obrázek. Dokažte, že součet obsahů těchto tří trojúhelníků je roven alespoň jedné třetině obsahu trojúhelníku ABC. (PLA-2019/PU8)

    

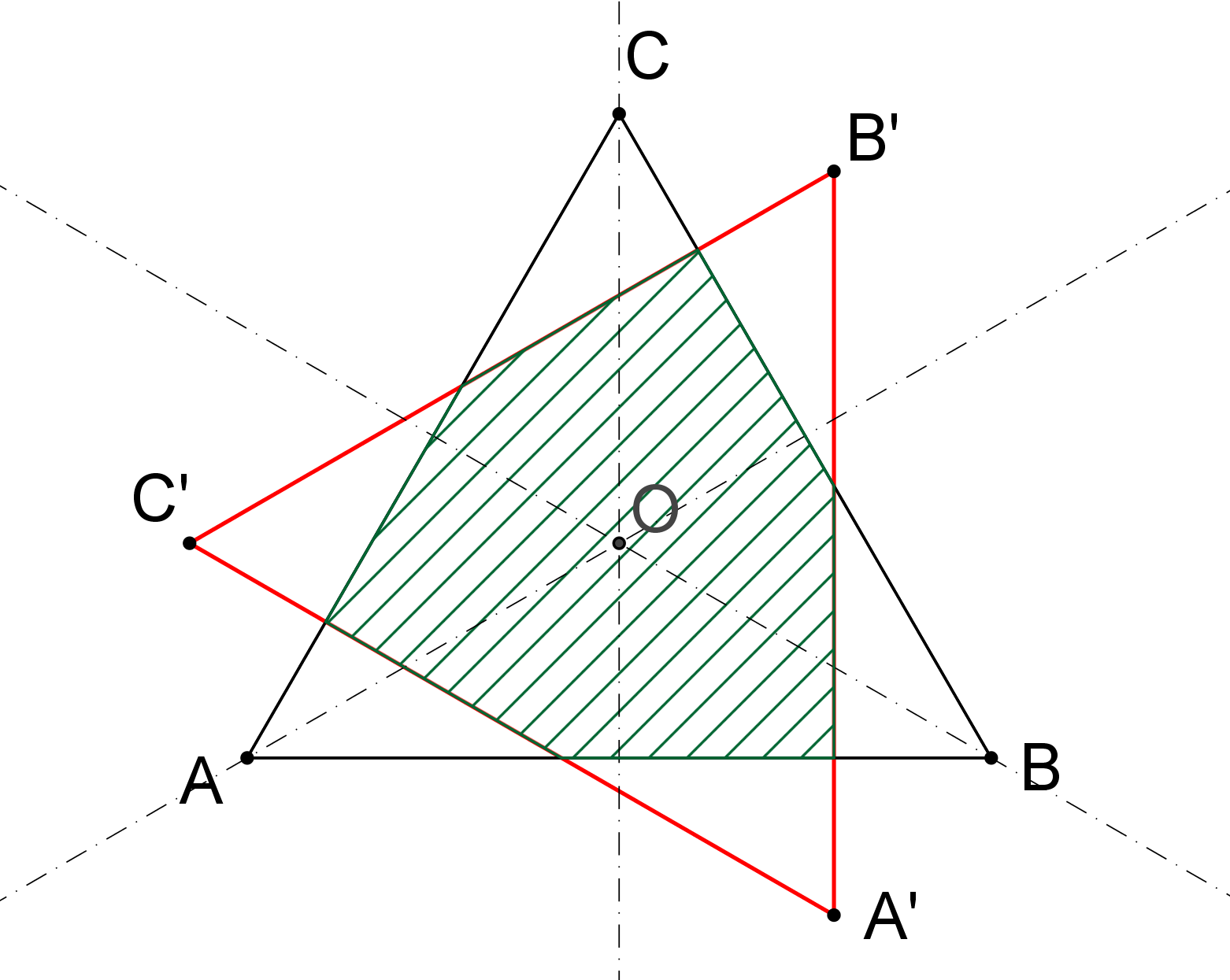
30. Rovnostranný trojúhelník ABC o dělce strany 4 cm otočíme kolem jeho průsečíku výšek o 90°, dostaneme tak trojúhelník A'B'C', viz obrázek. Určete obsah průniku trojúhelníků ABC a A'B'C'. (PLA-2019/PU9)

    

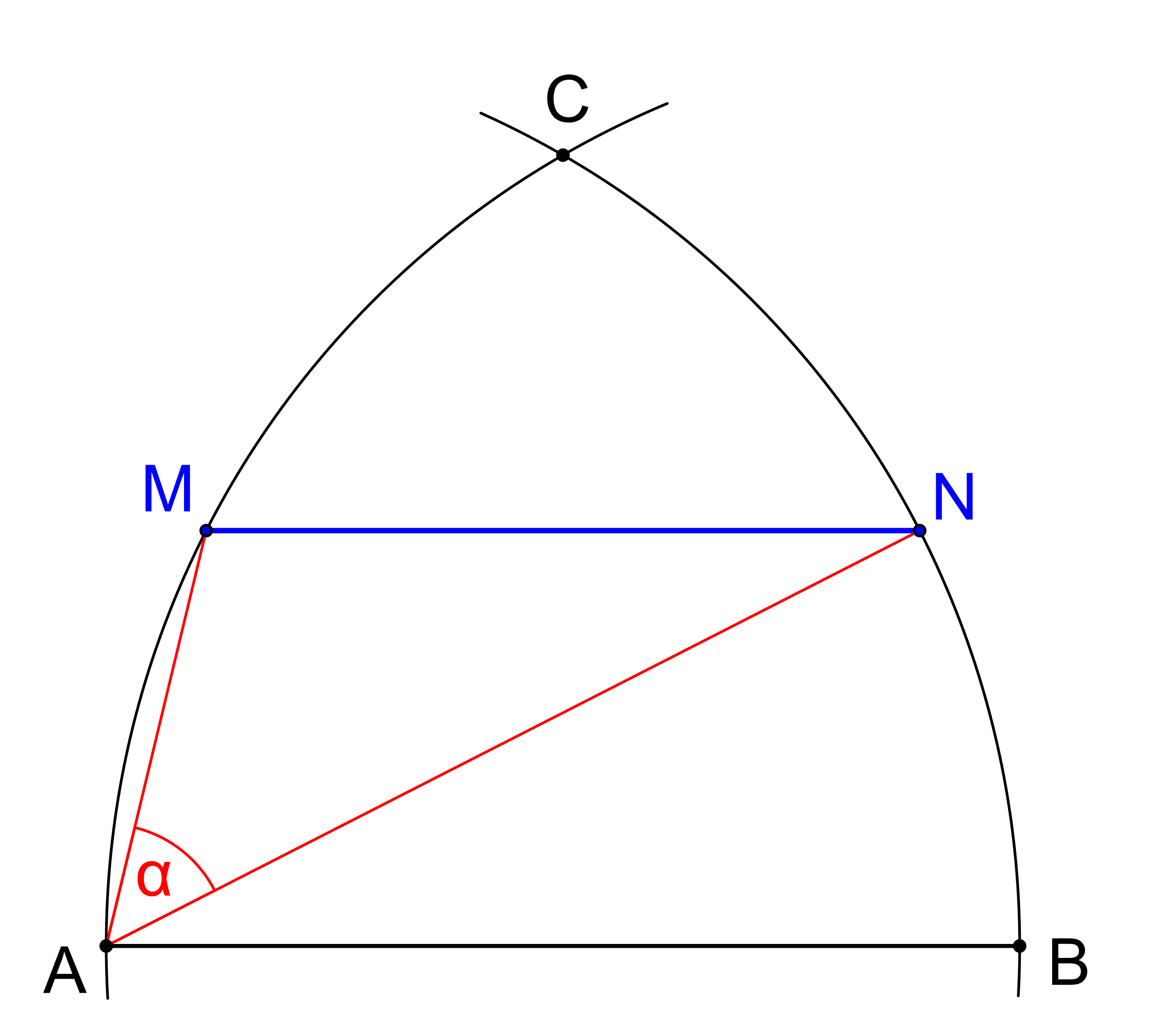
31. V roce 1902 zadal J. R. Vaňaus čtenářům Časopisu pro pěstování mathematiky a fysiky, ročník 31, číslo 3, následující úkol:
    Poloměrem AB opsány jsou z bodů A, B kruhové oblouky protínající se v bodě C. Ustanoviti jest v oblouku AC bod M a v oblouku BC bod N tak, aby MN bylo rovnoběžno k AB, a úhel MAN aby rovnal se danému ostrému úhlu. (viz Časopis pro pěstování mathematiky a fysiky, vol. 31, 3, Úloha 36, str. 262). Navrhněte postup řešení této úlohy. (PLA-2019/PU10)

    

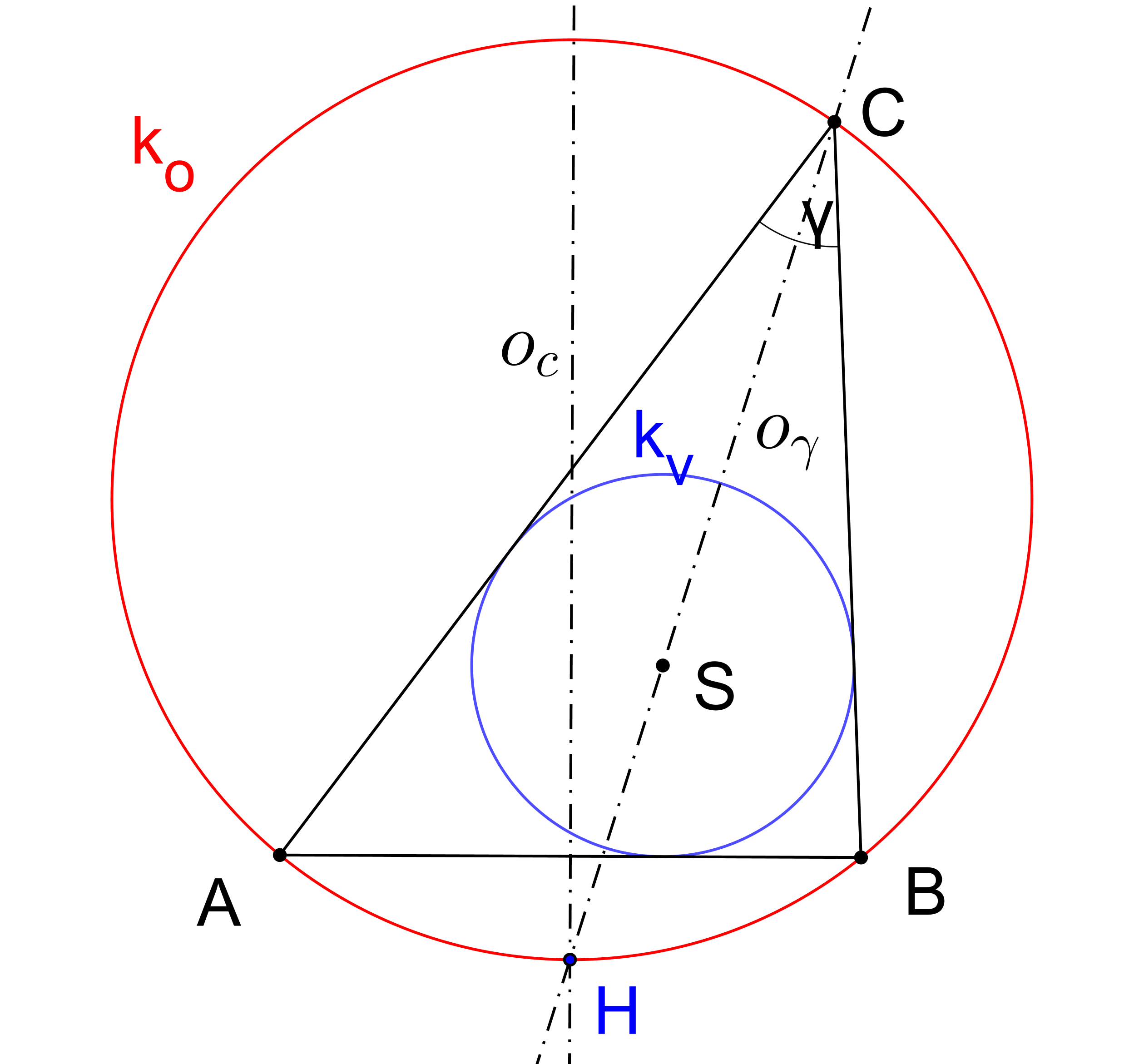
32. Dokažte následující větu: Buď ABC trojúhelník takový, že |BC| je různé od |AC|. Potom osa úhlu ACB protíná osu strany AB v bodě H, který leží na kružnici trojúhelníku ABC opsané. Dále platí, že |HA|=|HB|=|HS|, kde S je střed kružnice trojúhelníku vepsané. (PLA-2019/PU11)

    

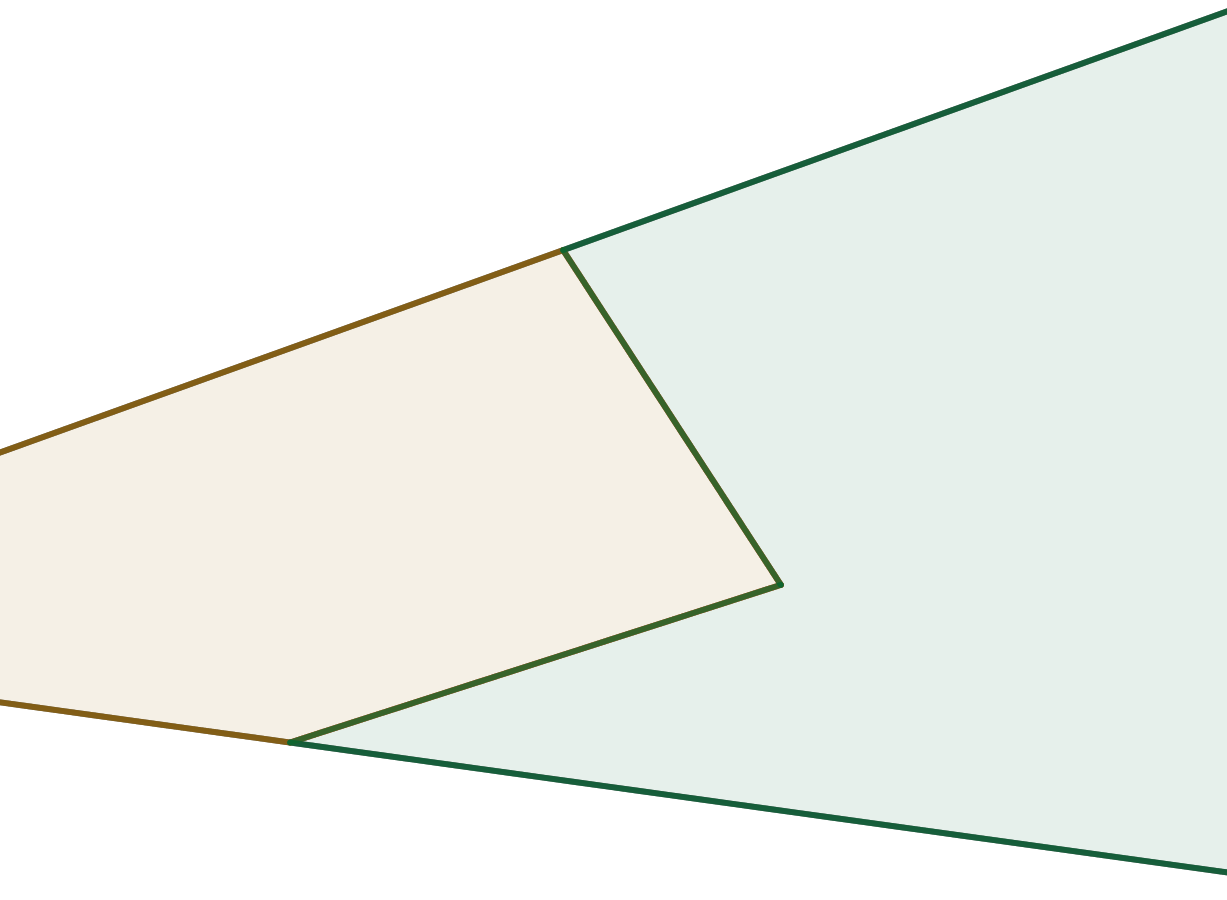
33. Na obrázku jsou znázorněny hranice dvou pozemků. Jejich společná hranice je tvořena lomenou čarou. Nahraďte jí úsečkou tak, aby výměra zahrad zůstala zachována. (PLA-2020/PU1)

    

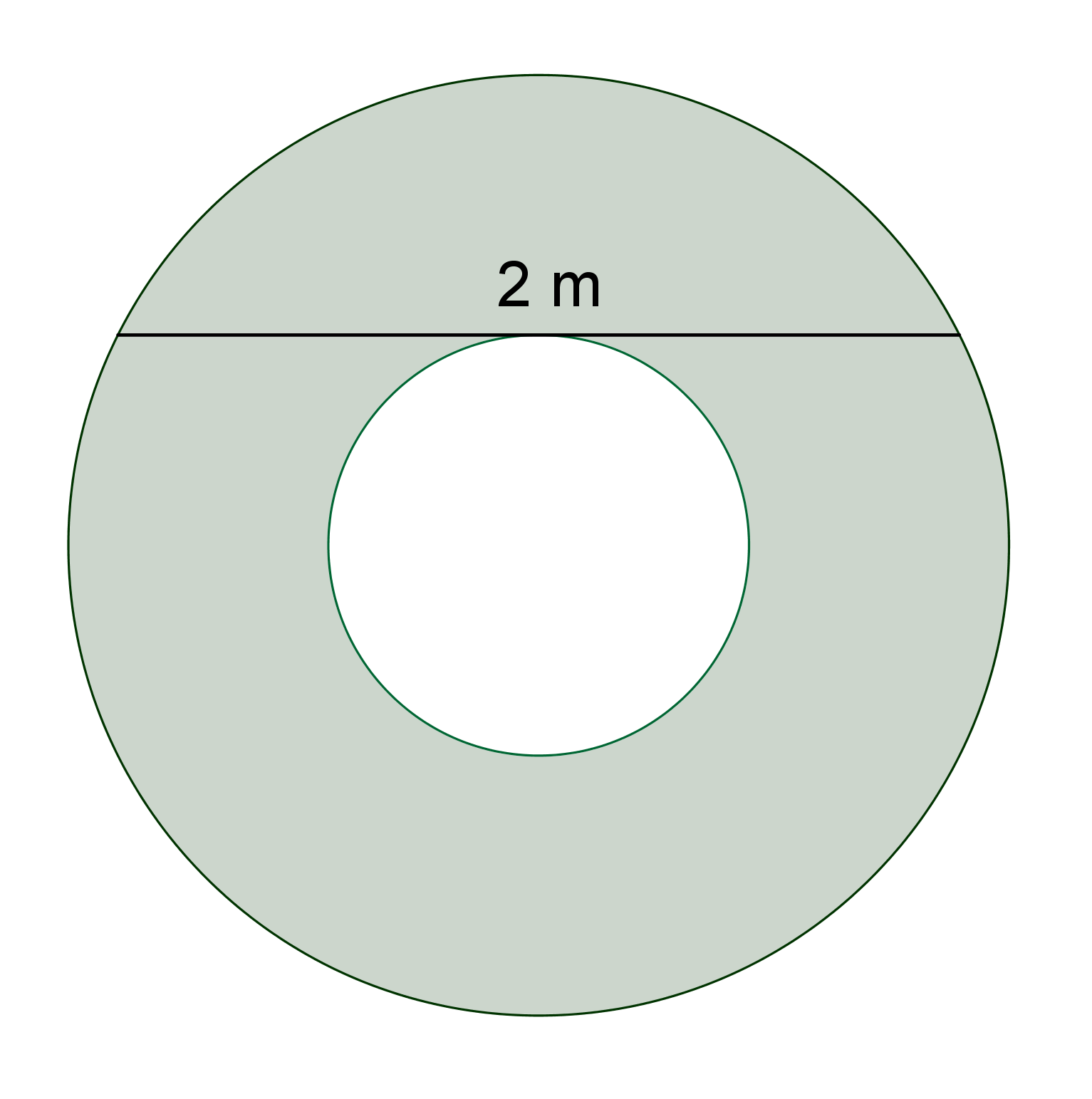
34. Určete velikost vybarveného mezikruží, je-li délka tětivy tečné k jeho vnitřní hraniční kružnici 2 m, viz obrázek. (PLA-2020/PU2)

    

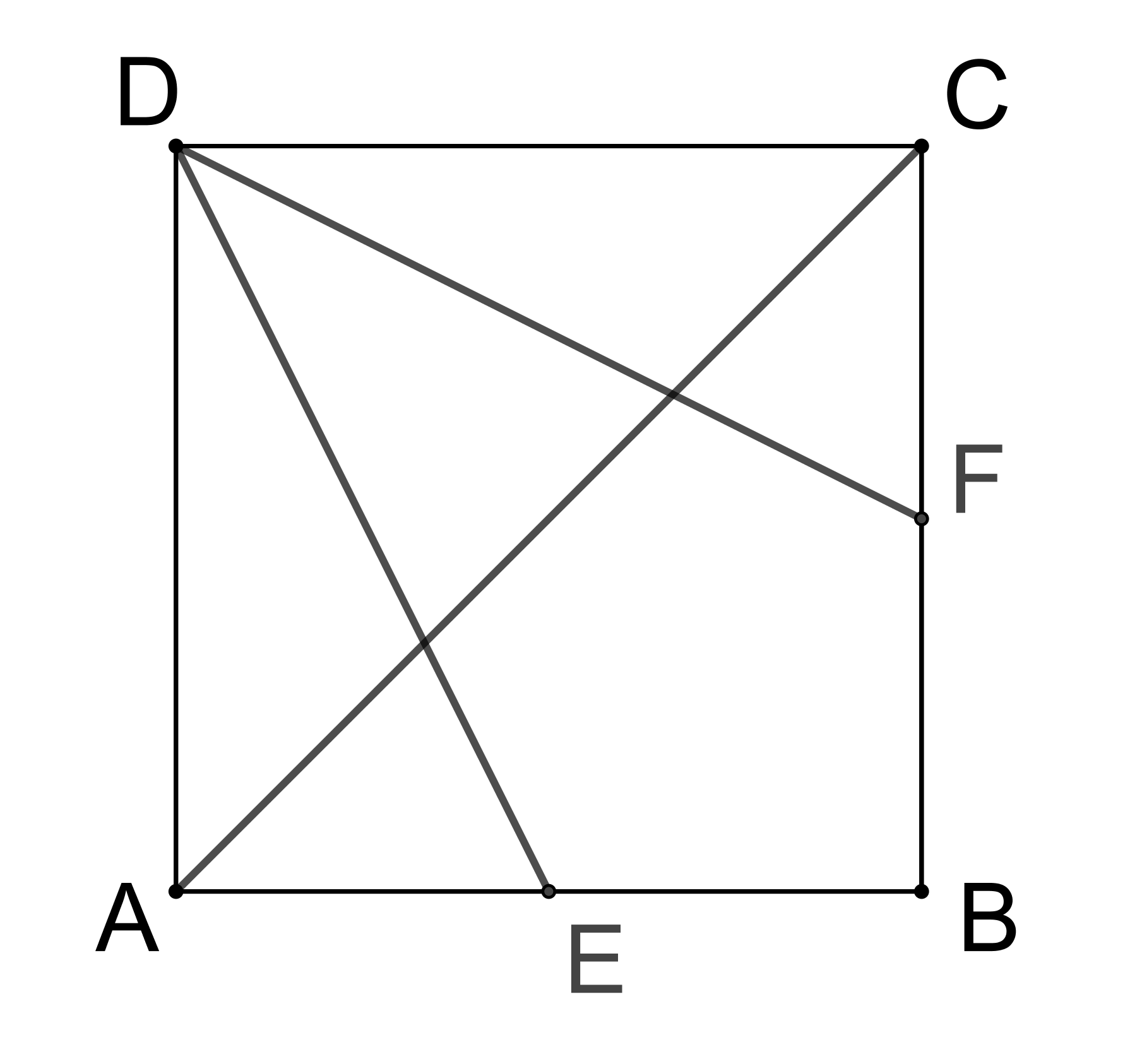
35. Úhlopříčka AC čtverce ABCD je rozdělena na tři části dvěma příčkami, které spojují vrchol D se středy E a F stran AB a BC, viz obrázek. Rozhodněte, zda jsou uvedené tři části úhlopříčky AC stejně dlouhé. Pravdivost svého tvrzení dokažte! (PLA-2020/PU3)

    

36. Jaký je vzah mezi velikostmi úhlů α a β? Své tvrzení dokažte! (PLA-2020/PU4)

    

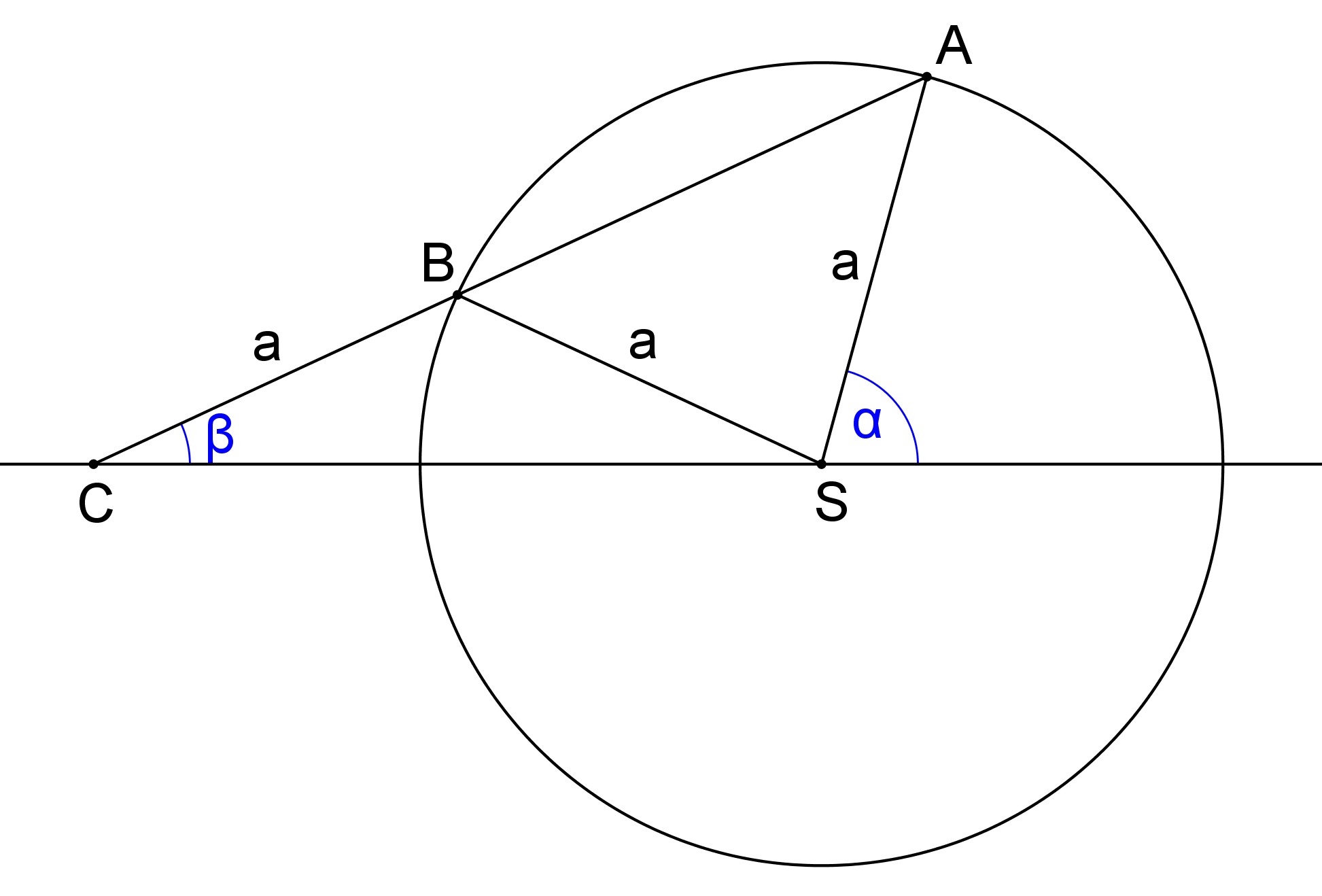
37. Jsou dány body X, Y a S, viz obrázek. Sestrojte čtverec ABCD tak, aby bod X ležel na přímce AB, bod Y na přímce BC a bod S byl středem čtverce. (PLA-2020/PU5)

    

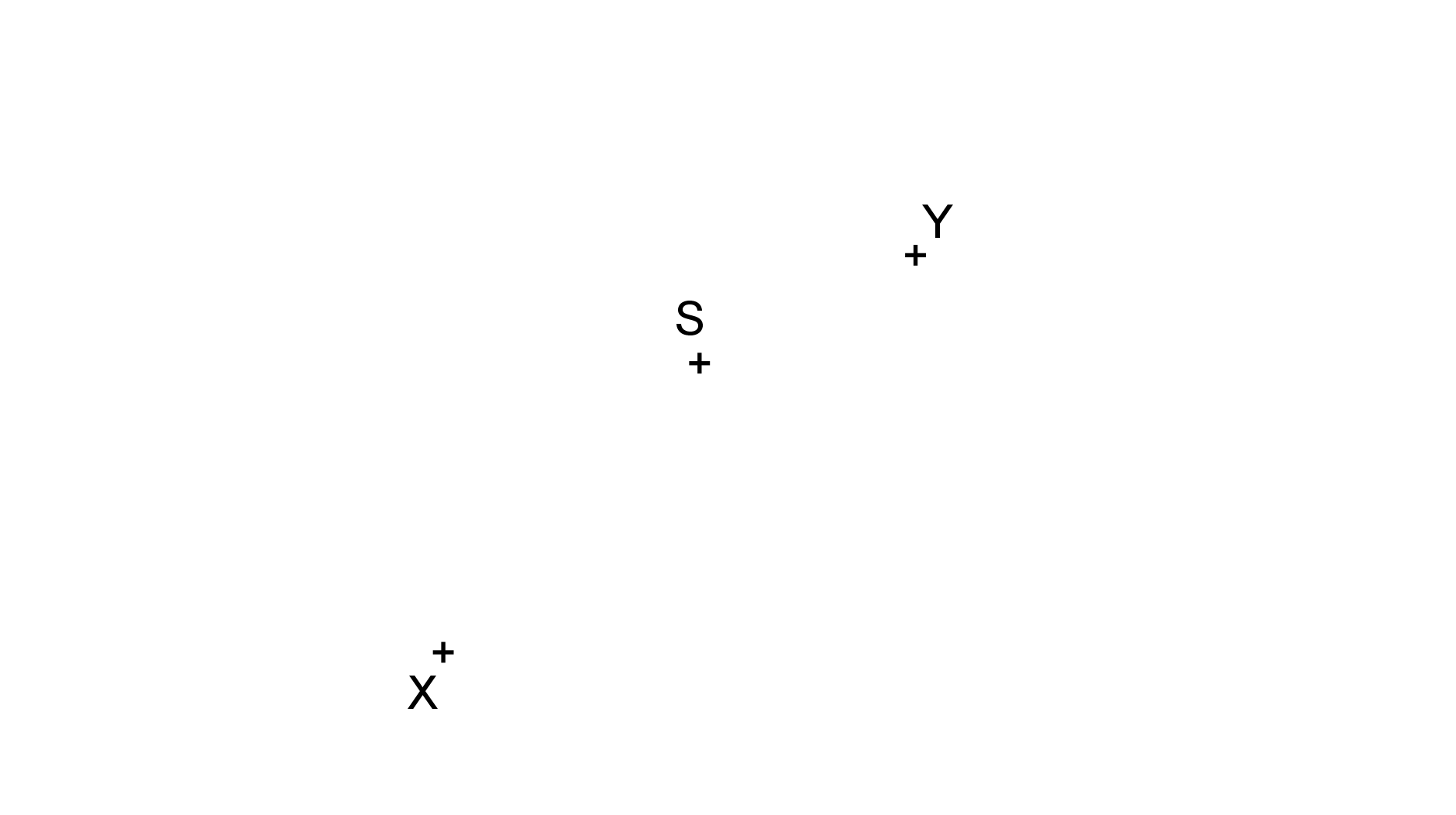
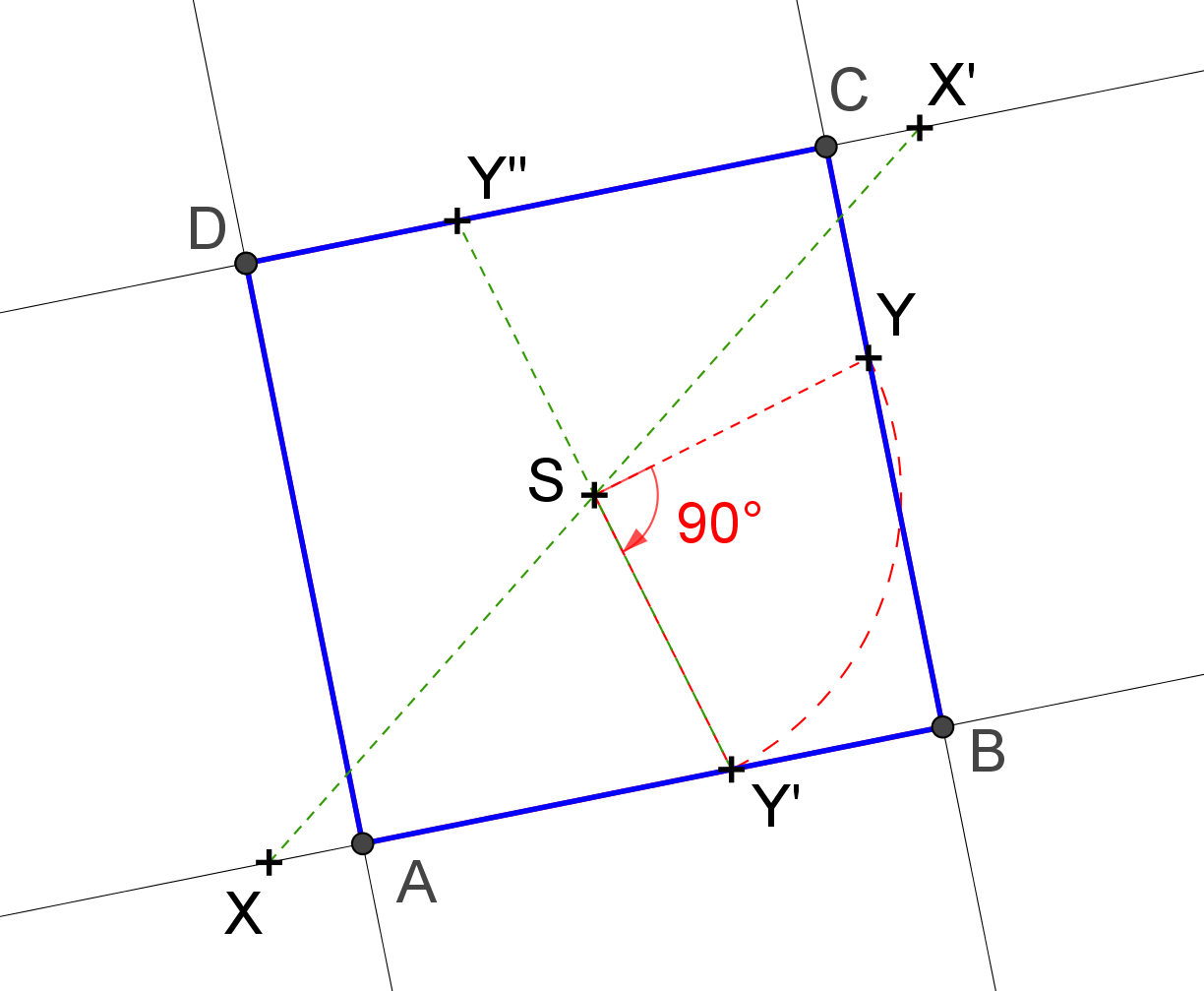
    Řešení: Postupujeme dle obrázku. Nejprve zobrazíme bod Y v otočení se středem S o úhel -90°. Výsledný bod Y', spolu s X potom zobrazíme ve středové souměrnosti se středem S. Dostaneme body Y'' a X'. Pak už máme dost bodů, abychom sestrojili celý čtverec. Upozorňuji, že toto není jediný postup. Například ti, kteří poslali svá řešení, používali různé jiné postupy, vždy však založené na principu zobrazení jedné strany čtverce na jeho jinou stranu, sousední nebo protilehlou.

    

38. Ze čtverce byl vystřižen kříž tvořící síť krychle, viz obrázek. Určete procento odpadu! (PLA-2020/PU6)

    

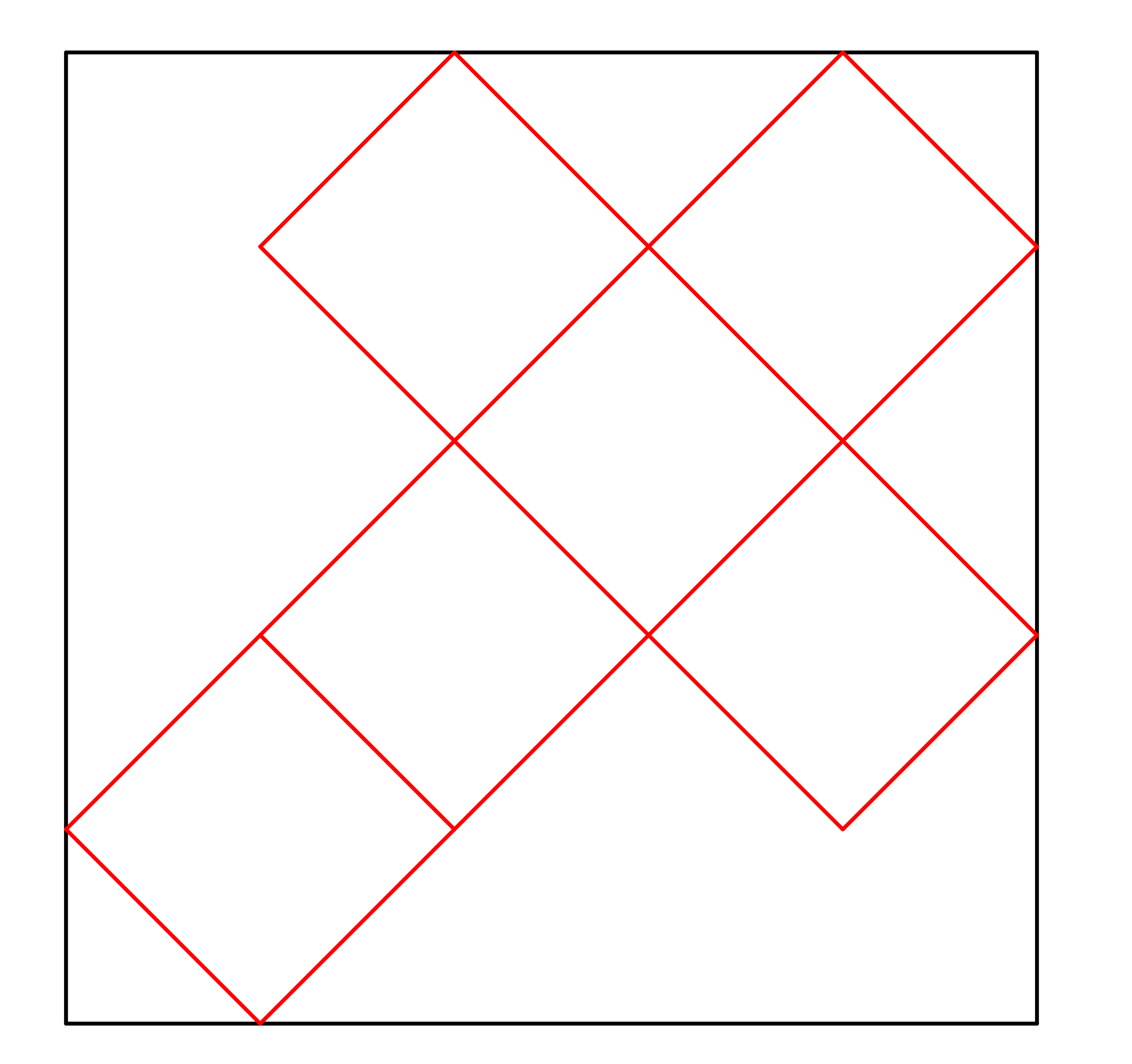
    Řešení:

    

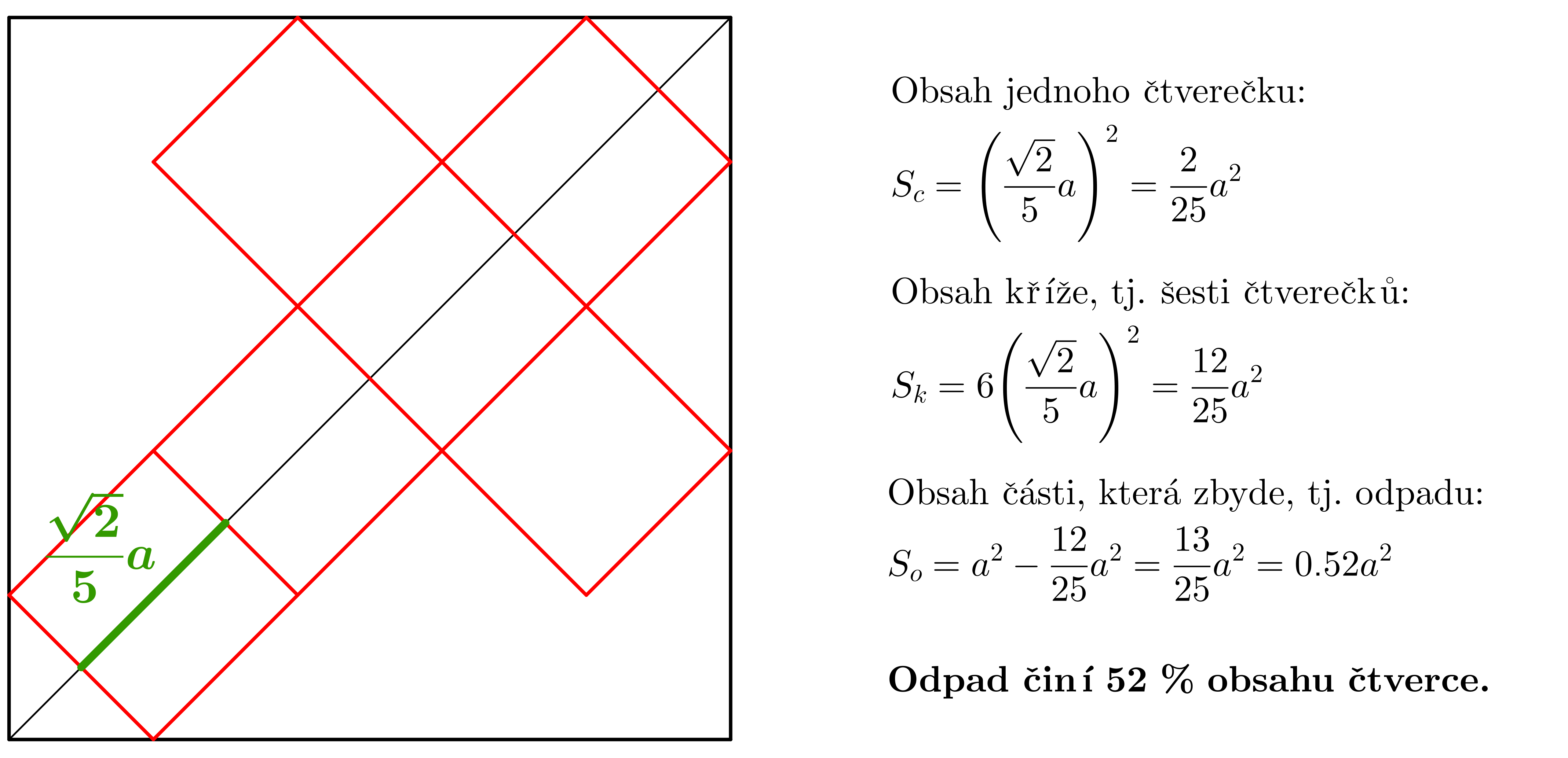
39. Určete délku strany největšího čtverce, který lze vepsat do jednotkové krychle. Jinak řečeno, jaký největší pevný čtverec můžete vložit do krychlové krabice o délce hrany 1 m? (PLA-2020/PU7)

    

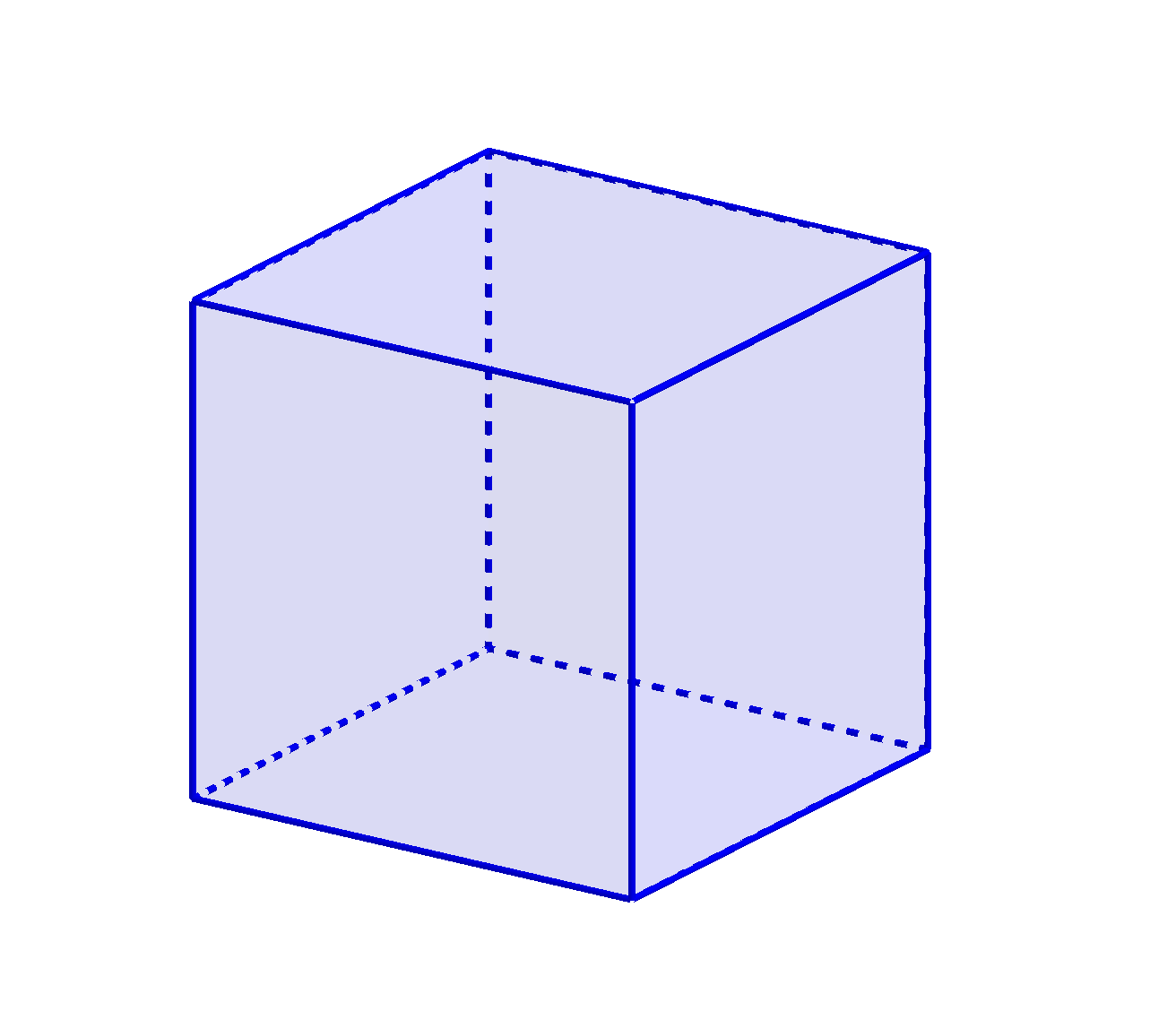
    Řešení: Vyřešení daného problému je klíčovým krokem při řešení otázky známé jako problém krychle prince Ruperta, viz Prince Rupert's cube: Jakou největší krychli můžeme protáhnot otvorem vytvořeným v jednotkové krychli?. Námi hledaný čtverec je obrysem tohoto otvoru. Délka jeho strany je 3√2/4≈1,06. Více viz Wikipedia: Prince Rupert's cube nebo WolframMathWorld: Prince Rupert's Cube, případně The cube shadow theorem (pt.1): Prince Rupert's paradox (video).

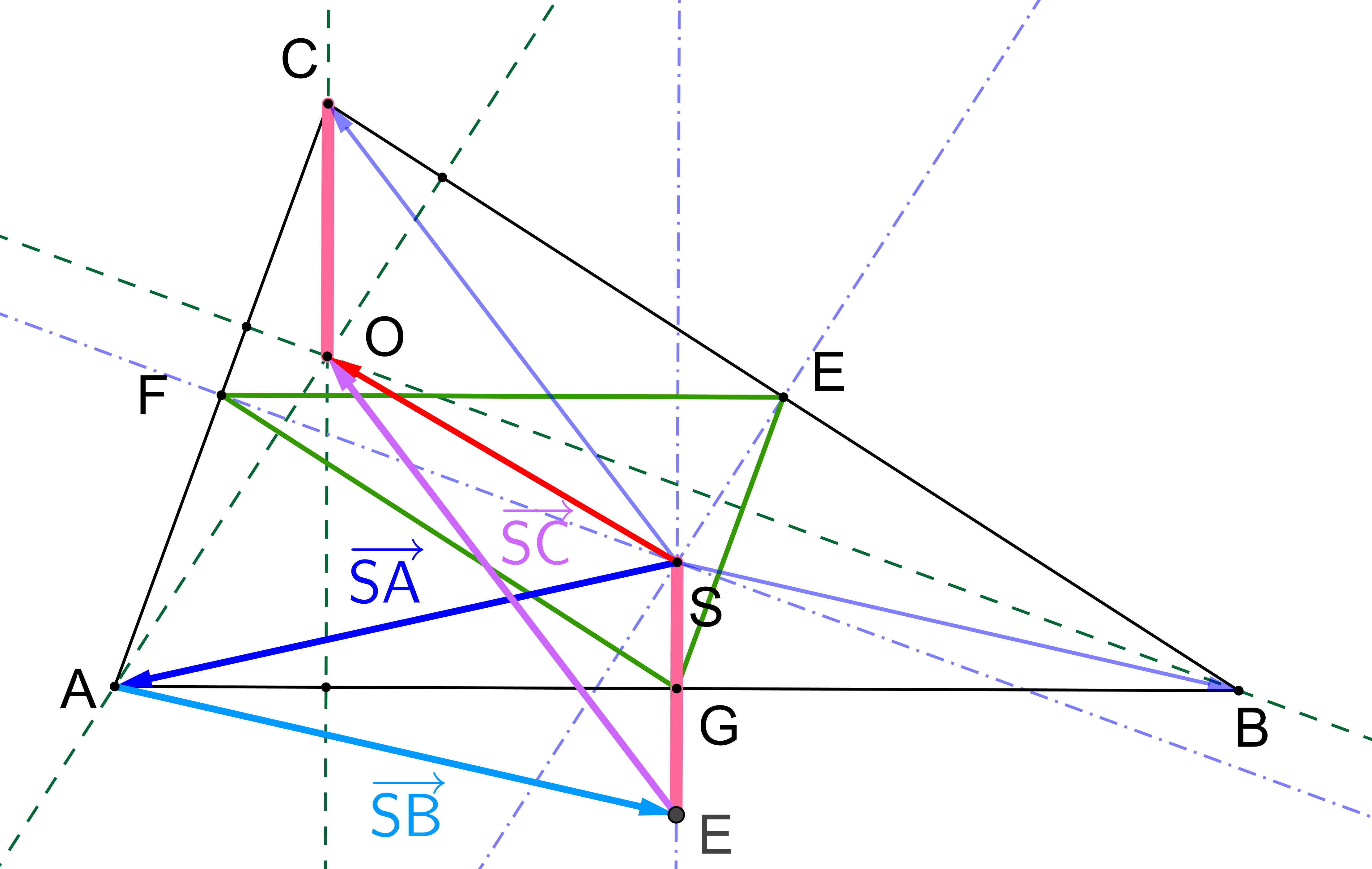
40. V trojúhelníku ABC je S průsečíkem os stran (tj. střed kružnice opsané) a O průsečíkem výšek (tj. ortocentrum), viz obrázek. Dokažte, že součet vektorů SA, SB, SC je roven SO, tj. SA+SB+SC=SO. (PLA-2020/PU8)

    

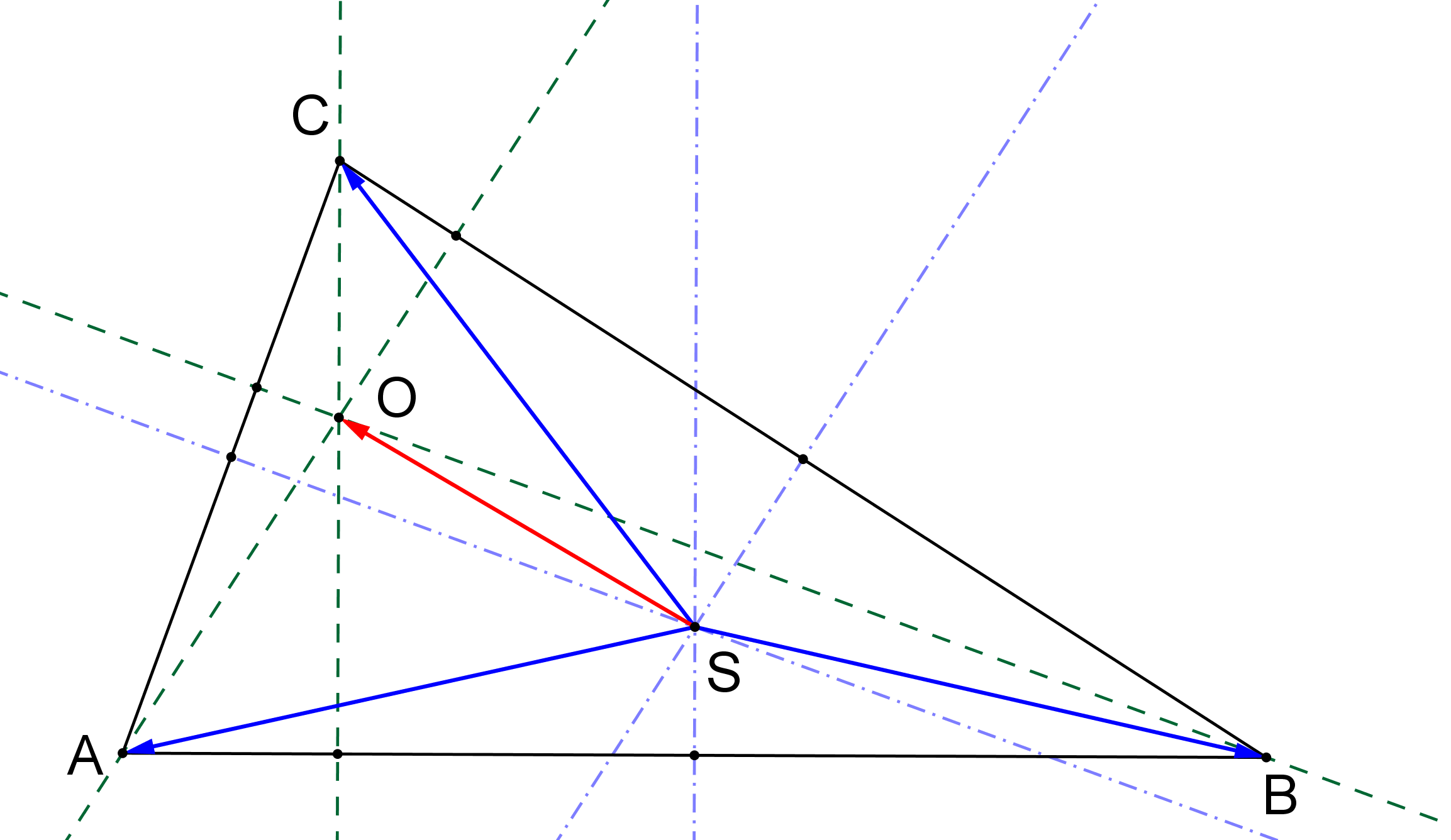
    Nápověda:

    

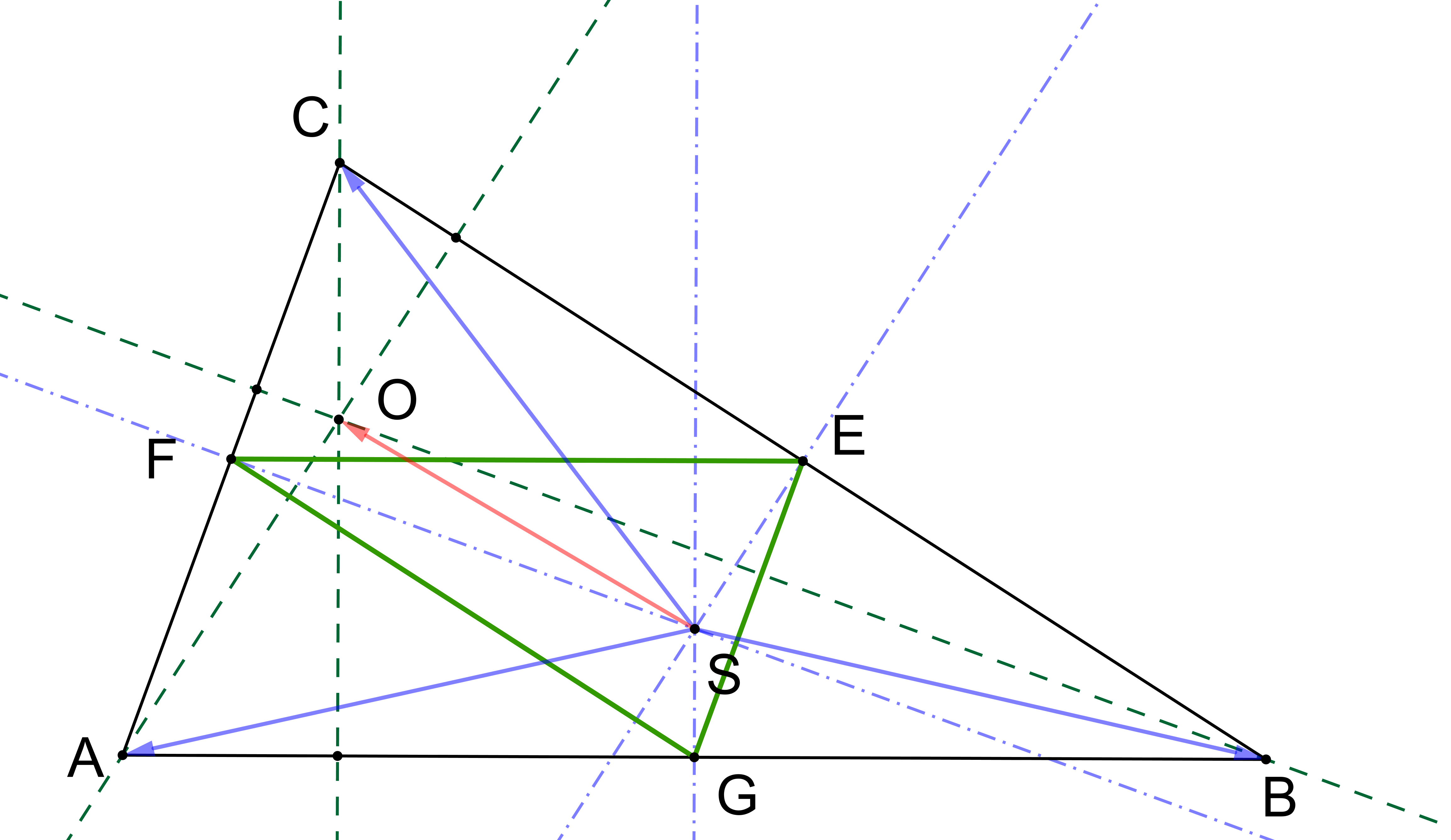
    Řešení: Sečteme-li postupně vektory SA, SB, SC (vytváříme z nich "řetěz", tj. do koncového bodu jednoho umístíme počáteční bod následujícího.) je zřejmé, že koncový bod posledního z nich, vektoru SC, leží na výšce v_c trojúhelníku ABC. Jde tedy "jenom" o to, ukázat, že leží právě v bodě O. To, jak vidíme na obrázku nastane tehdy, když |CO|=|SE|. To ale plyne například ze skutečnosti, že trojúhelník EFG je podobný trojúhelníku ABC s poměrem podobnosti 1/2 (jeho strany jsou středními příčkami trojúhelníku ABC) a že bod S je jeho ortocentrum (osy stran trojúhelníku ABC jsou výškami trojúhelníku EFG, kde výškami rozumíme přímky jdoucí vrcholy trojúhelníku kolmo na protilehlé strany).

    

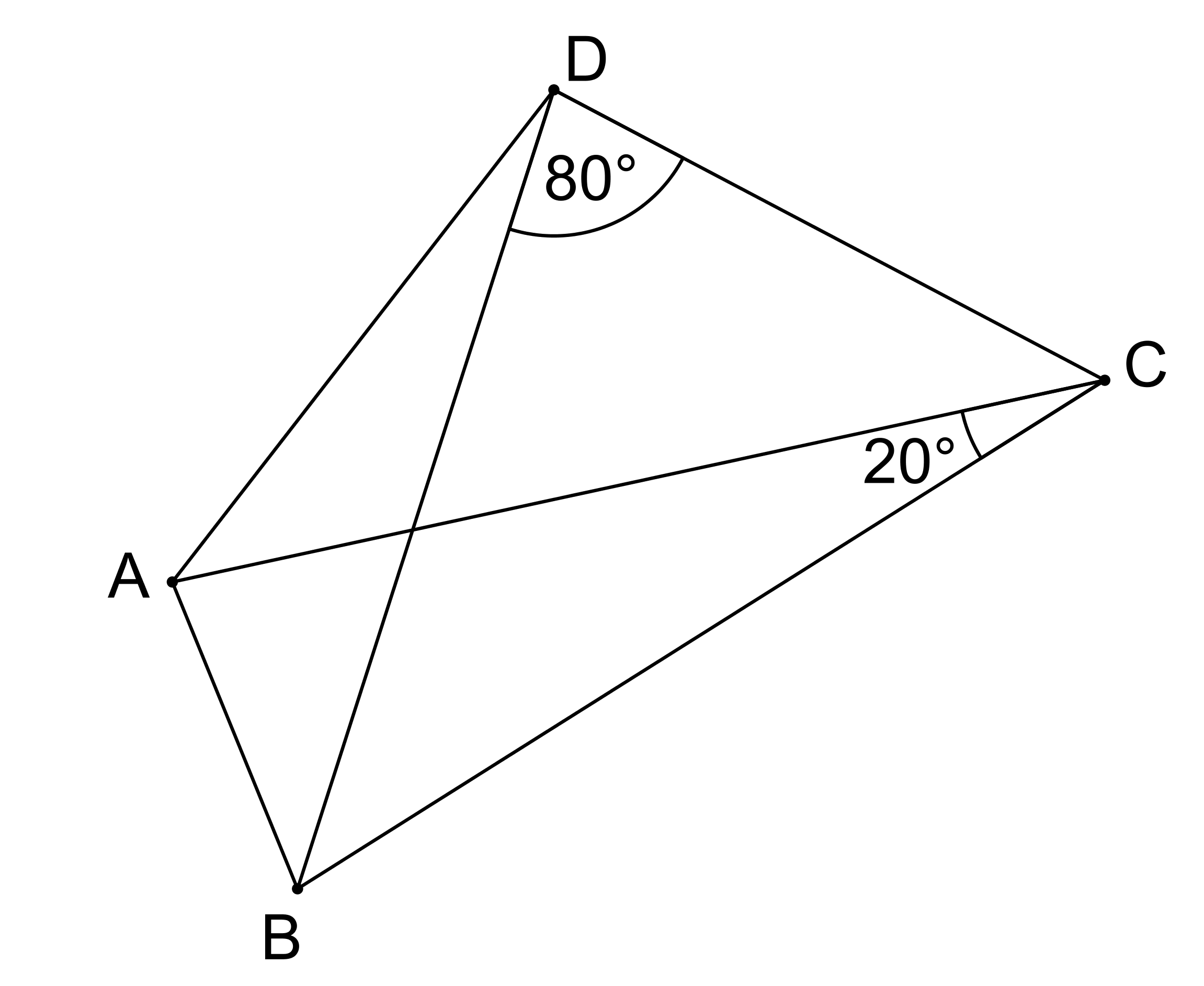
41. V konvexním čtyřúhelníku ABCD je úhlopříčka BD osou vnitřního úhlu ∠ABC a dále platí |AC|=|BC|. Velikost úhlu ∠BDC je 80° a velikost úhlu ∠ACB je 20°. Určete velikost úhlu ∠BAD! (PLA-2020/PU9)

    

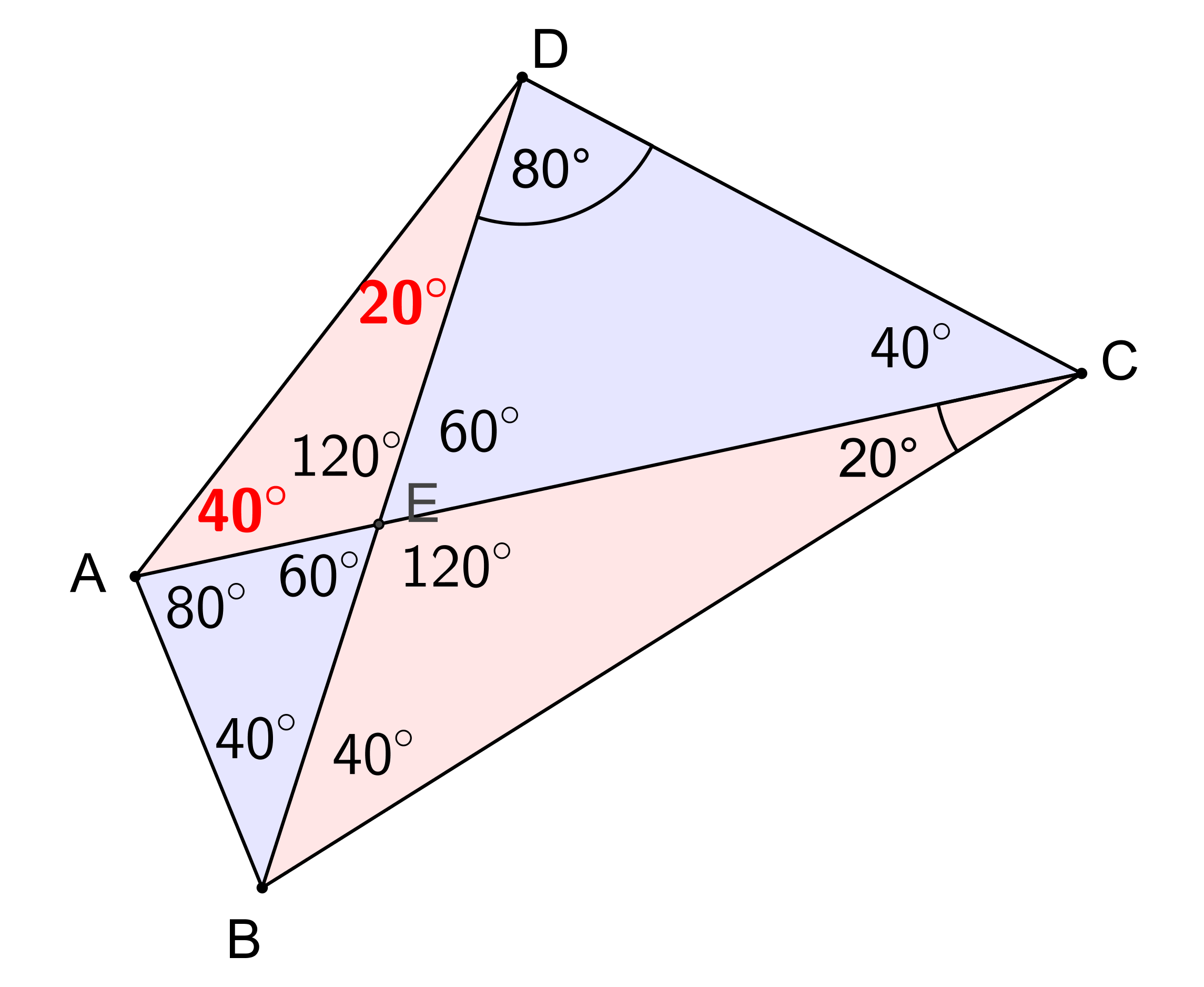
    Řešení: Viz obrázek. Celkem snadno zjistíme velikosti úhlů, které v obrázku figurují, s výjimkou vnitřních úhlú trojúhelníku DAE při vrcholech D a A, o kterých víme, že jejich součet je 60°. O jejich velikostech nám pomohou rozhodnout podobnosti trojúhelníků, které vyplňují daný čtyřúhelník. Konkrétně je zjevné, že trojúhelník ABE je podobný trojúhelníku DCE. Potom ale musí být trojúhelník ADE podobný trojúhelníku BCE. Pak už je jasné, že při vrcholu A je úhel 40° a při D je 20°.

    

42. Ve čtyřúhelníku ABCD jsou úhlopříčkami AC a BD a jim protilehlými vrcholy tvořeny čtyři trojúhelníky ACD, DBC, CAB a BDA. Dokažte, že strany čtyřúhelníku EFGH, kde E, F, G a H jsou v daném pořadí těžiště uvedených trojúhelníků, jsou rovnoběžné se stranami čtyřúhelníku ABCD a jejich délky jsou třetinami těchto stran. (PLA-2020/PU10)

    

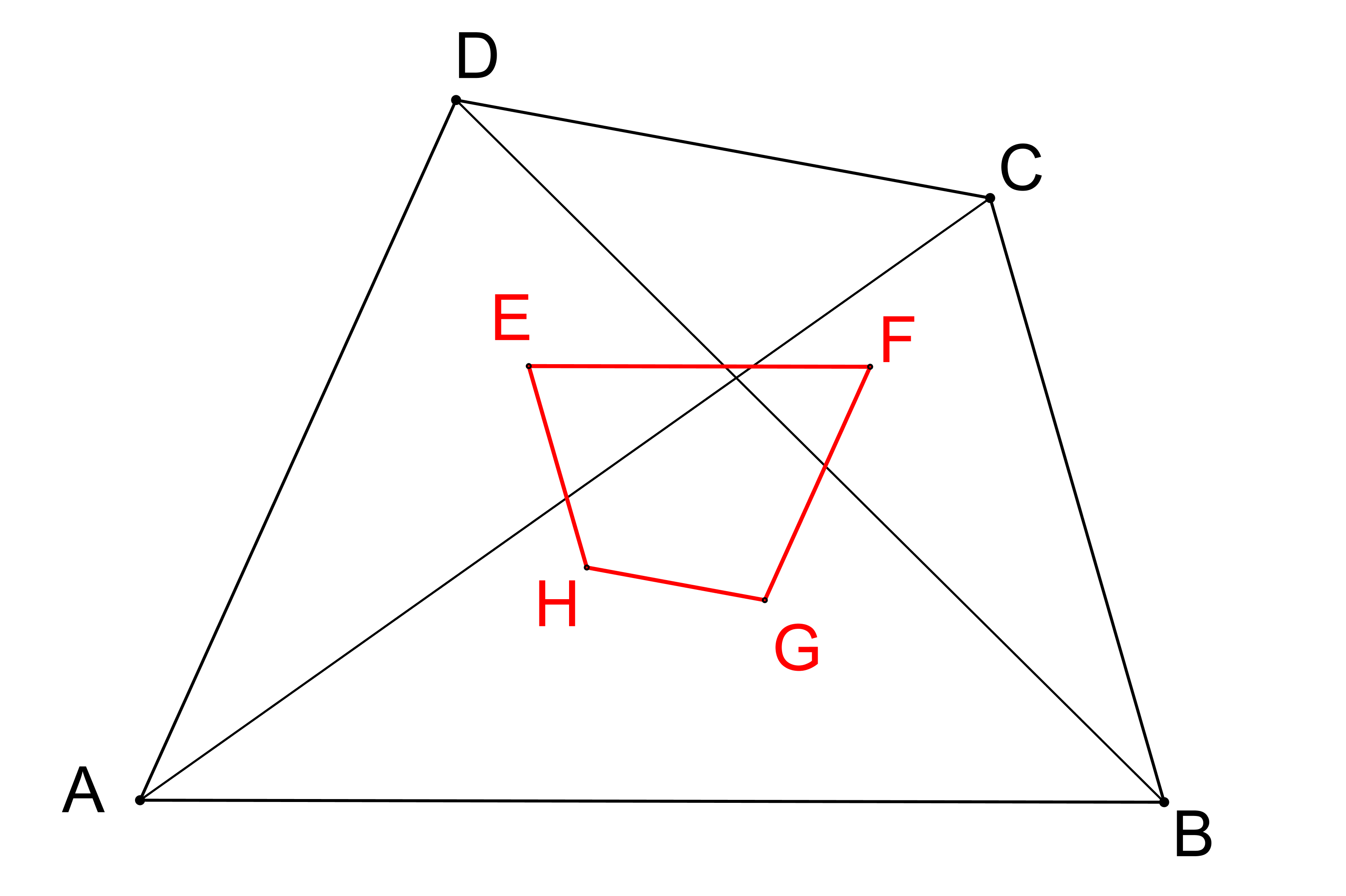
    Řešení: Existuje více způsobů, jak úlohu řešit. Ukáži zde takový, který nikdo z řešitelů nepoužil. Využiji k tomu vztah T=(A+B+C)/3 pro výpočet souřadnic těžiště T trojúhelníku ABC. Podle zadání úlohy pak platí E=(A+C+D)/3 a F=(D+C+B)/3 a vektor F-E, jehož umístěním je úsečka EF, má souřadnice F-E=(D+C+B)/3-(A+C+D)/3=(B-A)/3. Vidíme, že F-E je skutečně rovnoběžný s B-A a je třikrát menší. Analogicky dokážeme tyto vlastnosti i pro zbývající tři strany čtyřúhelníku EFGH.

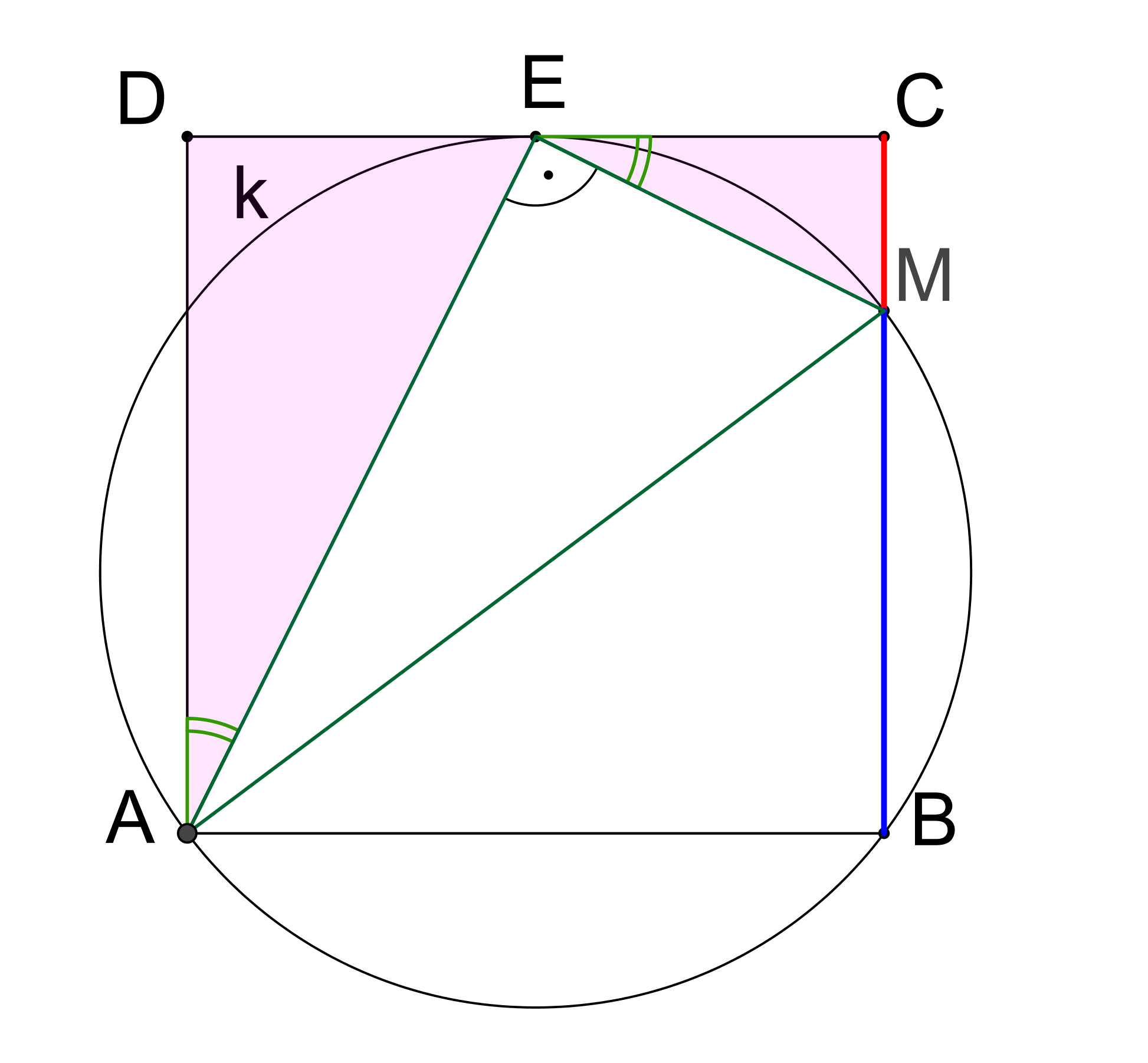
43. V rovině je dán čtverec ABCD. Kružnice k prochází body A, B a dotýká se přímky CD. Označme M průsečík kružnice k a strany BC (různý od B), viz obrázek. Určete poměr |CM|:|MB|. (PLA-2020/PU11)

    

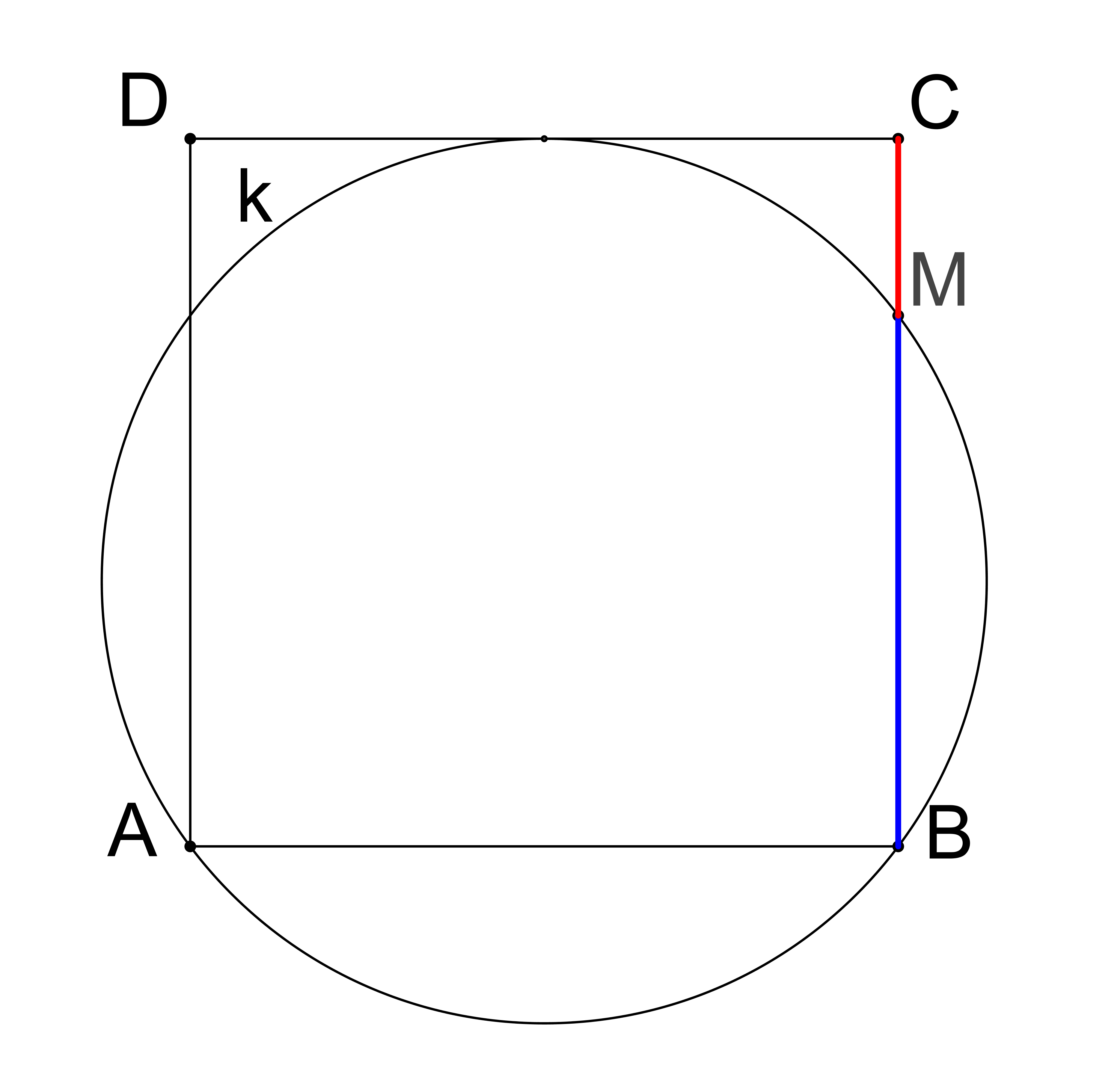
    Řešení: Trojúhelníky AED a EMC, viz obrázek, jsou podobné (Existuje věta, která říká, že jsou-li ramena dvou úhlů po dvojicích vzájemně kolmá, tyto úhly jsou shodné. To je situace vyznačených vnitřních úhlů uvedených trojúhelníků.). Potom platí |AD|/|EC| = |DE|/|CM|, po dosazení a/(a/2)=(a/2)/|CM|, odkud po úpravě plyne |CM|=a/4. Pro poměr |CM|:|MB| tedy platí |CM|:|MB| = 1:3.

    

44. V rovině je dán pravoúhlý trojúhelník ABC takový, že kružnice k(A,|AC|) protíná přeponu AB v jejím středu S. Dokažte, že kružnice opsaná trojúhelníku BCS je shodná s kružnicí k. (PLA-2020/PU12)

    

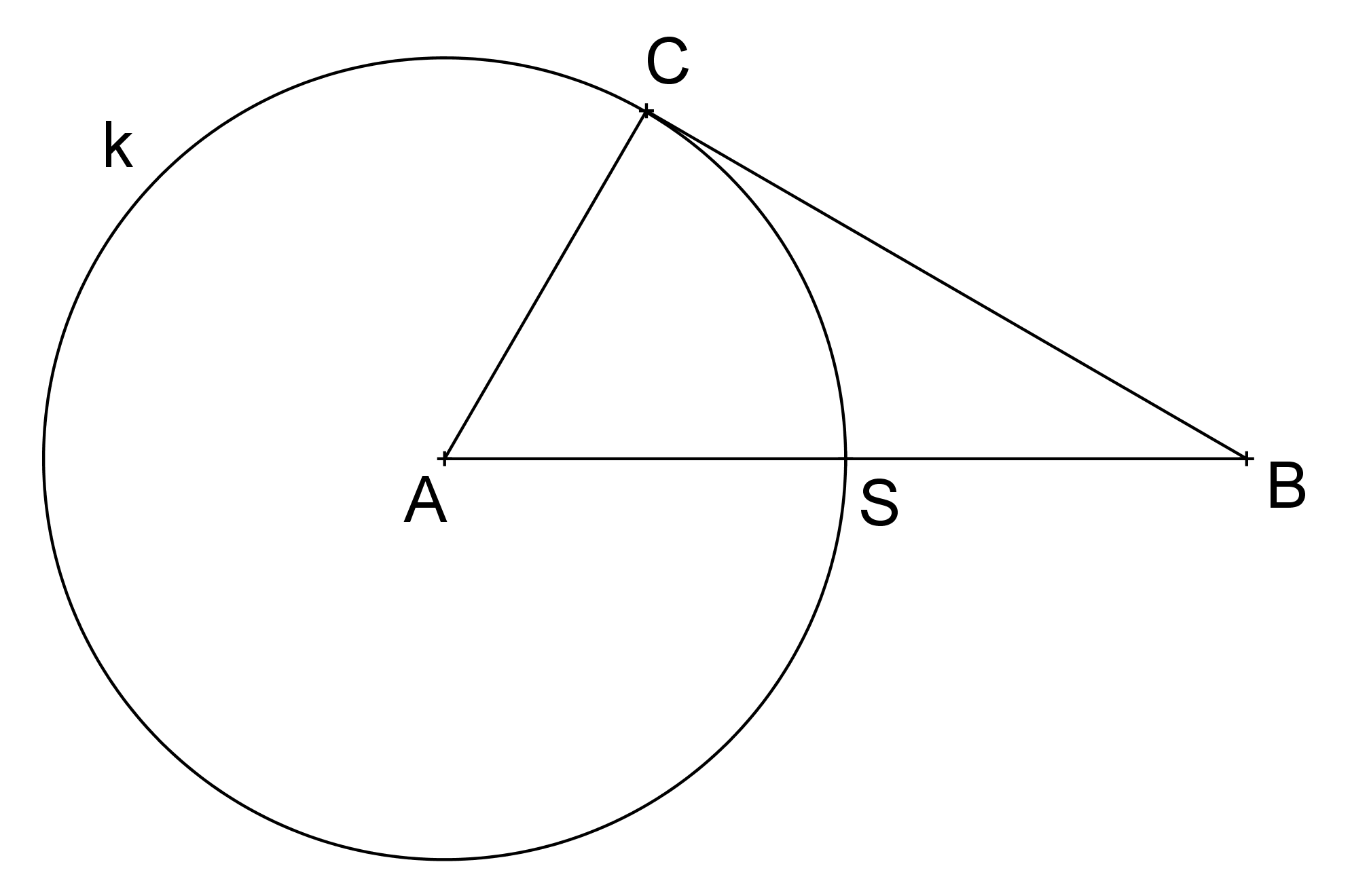
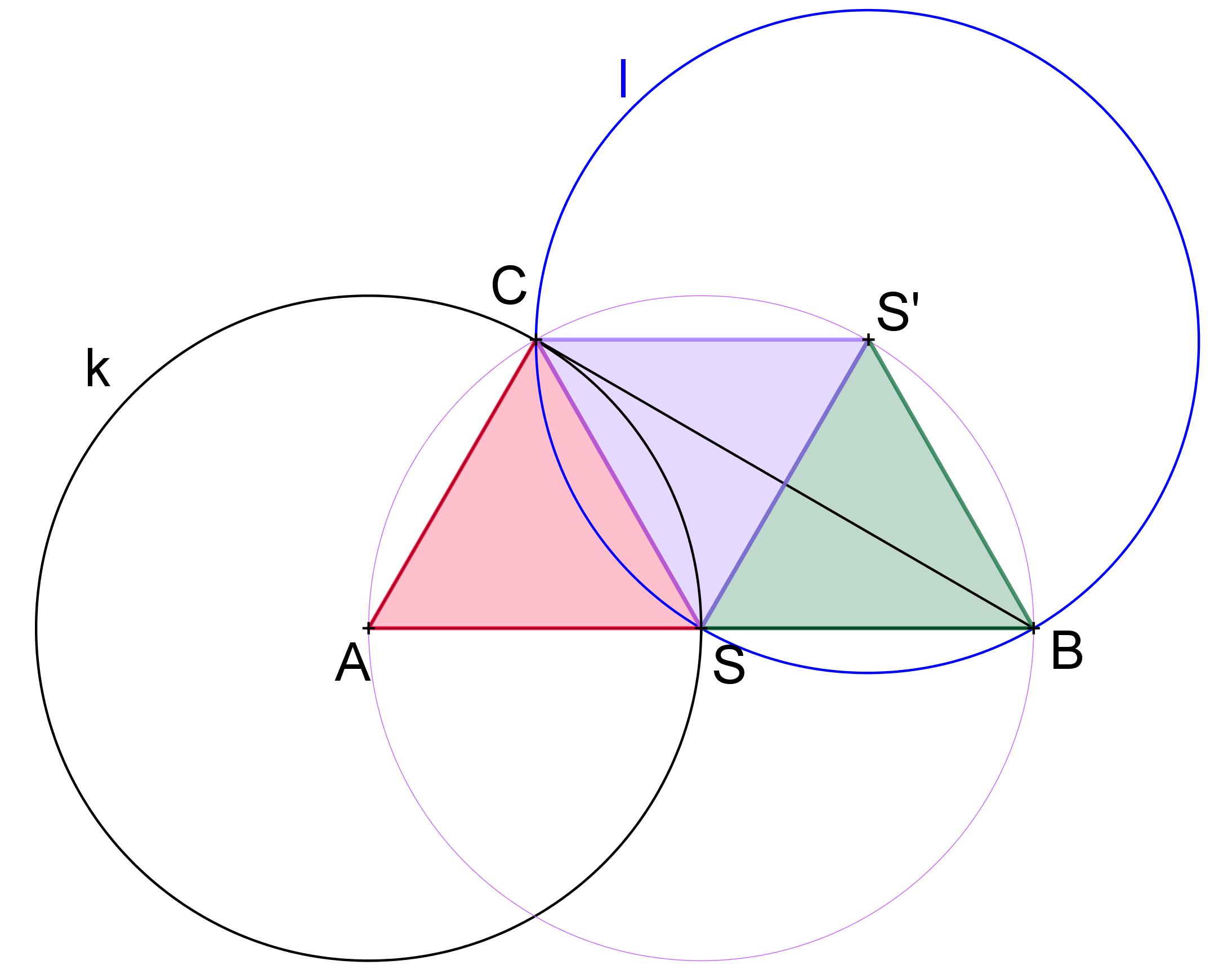
    Řešení: Stačí dokázat, že tři barevné trojúhelníky na obrázku níže jsou shodné rovnostranné trojúhelníky. Při použití Thaletovy kružnice a skutečností, že součet vnitřních úhlů v trojúhelníku je 180° a že osa tětivy prochází středem kružnice to není nijak obtížné.

    

45. Dvě spolu pevně spojená kola o různých poloměrech, větší o poloměru R, menší o poloměru r, se pohybují každé po své dráze, které jsou vzájemně rovnoběžné, viz obrázek. Větší kolo urazí dráhu 2πR, menší potom 2πr. Z obrázku je zřejmé, že 2πR = 2πr, tj. R = r, což ale neplatí. Kde je chyba? (PLA-2020/PU13)

    

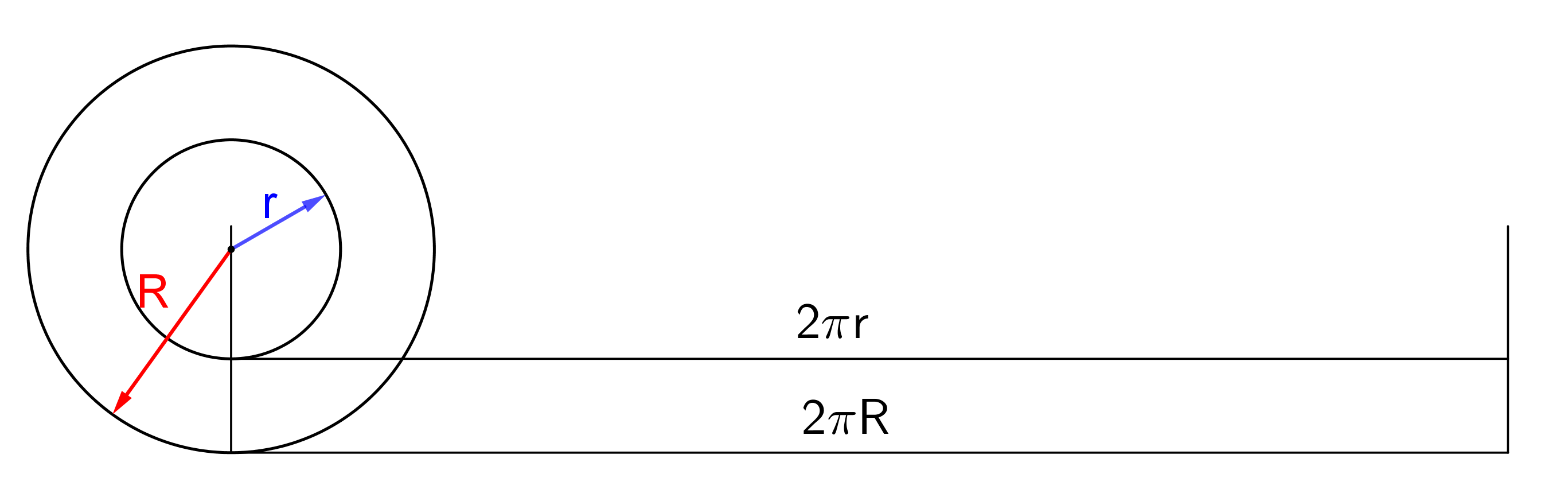
    Řešení: Obě kola se nemohou současně odvalovat (tj. pohybovat bez smyku), jedno z nich prokluzuje. Dle uvedeného zadání je to to malé.
    Jedná se o problém - paradox, jehož zadání je připisováno Aristotelovi. Proto je znám jako Aristotelovo kolo, viz např. Aristotle's wheel paradox

46. Zadání (pdf) (PLA-2020/PU14)

47. Čtverce ABCD a BFGE mají společný vrchol B, viz obrázek. Dokažte, že přímky AE a CF jsou pro každé takovéto čtverce kolmé. (GEO2-2020/PU1)

48. Uvažujme dvě kružnice k, l se společnými body A, B, viz obrázek. Pohybuje-li se bod P po oblouku BA, délka tětivy QR kružnice k je konstantní. Dokažte! (GEO2-2020/PU2)

    

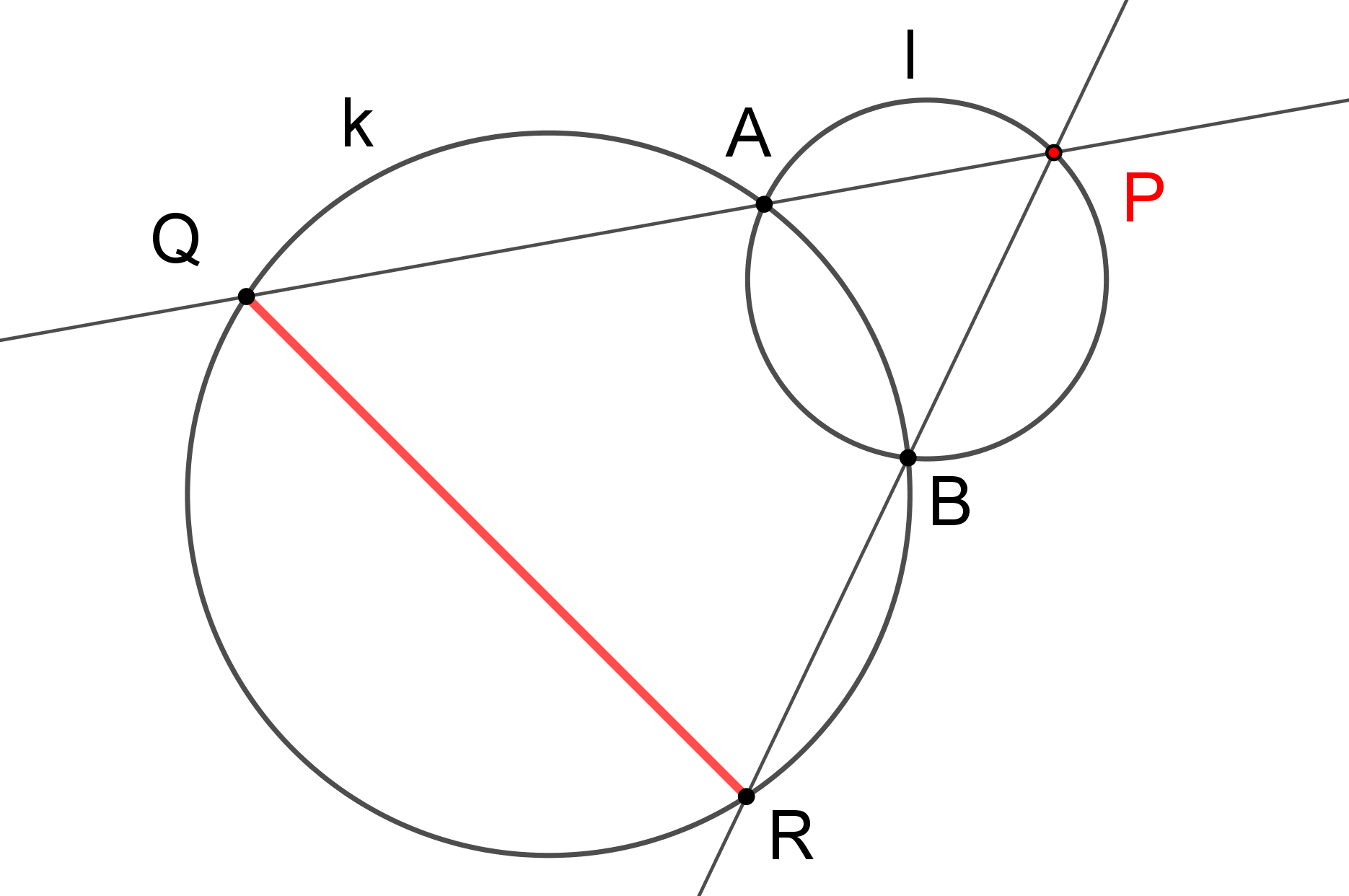
49. Dokažte, že pro libovolný rovnoběžník ABCD se stranami a, b a úhlopříčkami e, f, viz obrázek, platí

    e²+f²=2(a²+b²). (GEO2-2020/PU3)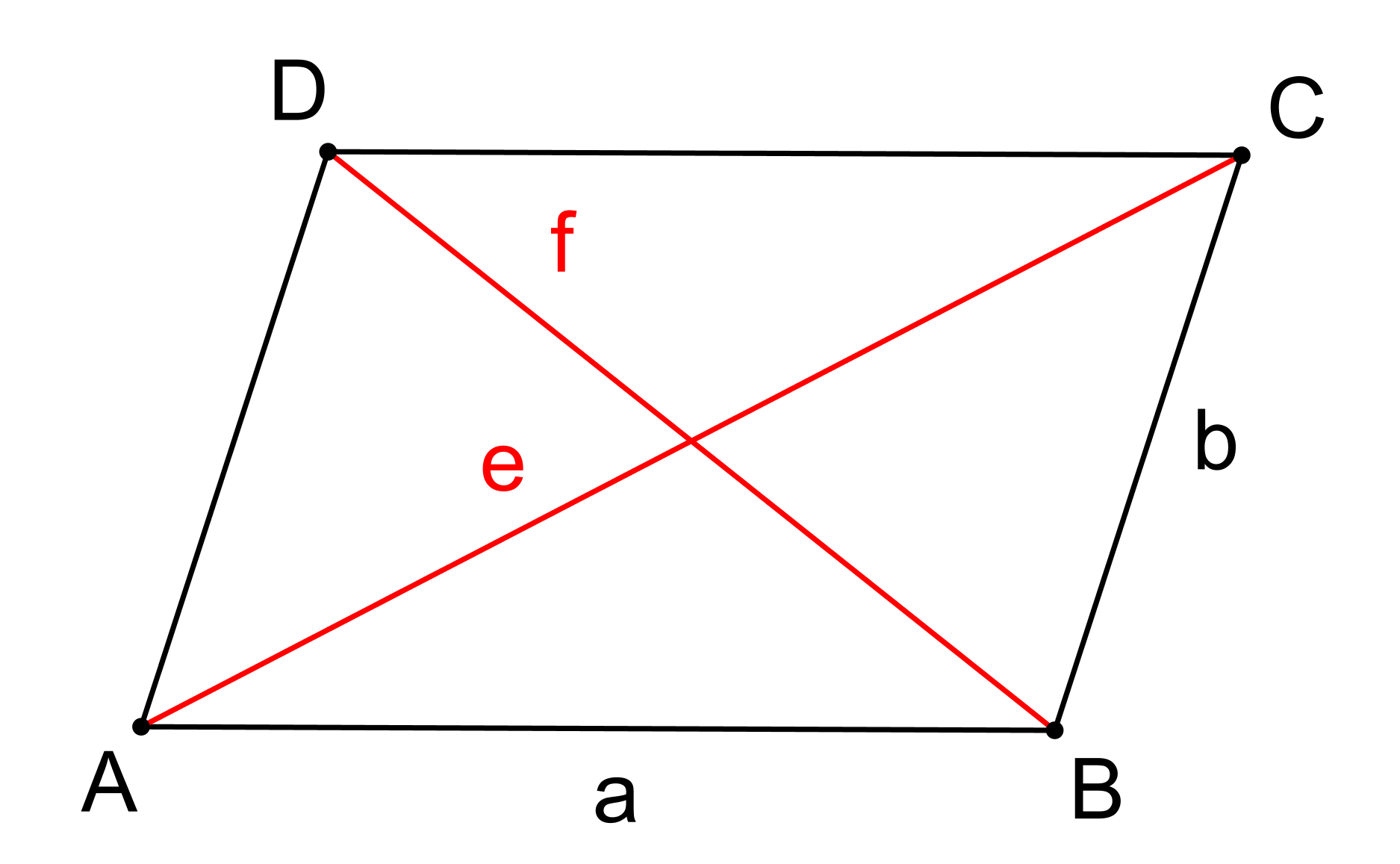

50. Dokažte, že pro trojboký jehlan A, B, C, D, který vznikne "uříznutím" z kvádru dle obrázku, platí

    S²_ABC=S²_ABD+S²_BCD+S²_ACD,
    kde S_ABC, S_ABD, S_BCD, S_ACD jsou obsahy stěn tohoto jehlanu. (GEO2-2020/PU4)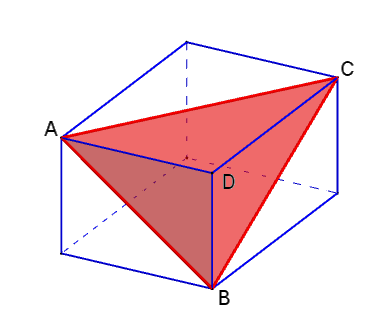

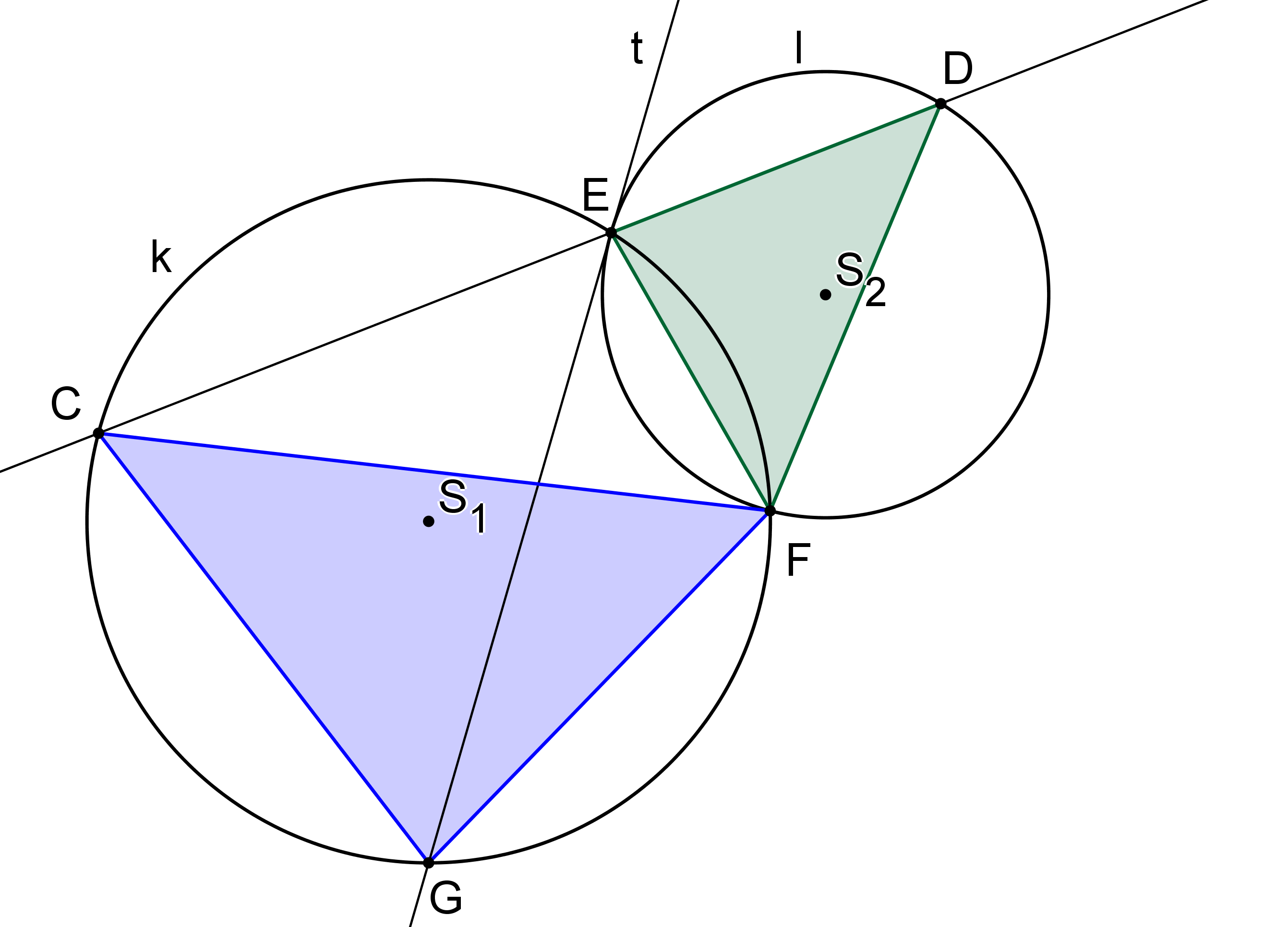
51. Jsou dány kružnice k, l protínající se v bodech E, F. Tečna kružnice l v bodě E protíná k v bodě G. Zvolme libovolný bod C na oblouku EG, viz obrázek, a sestrojme přímku CE, která protína kružnici l v bodě D. Dokažte, že trojúhelníky DEF a CGF jsou podobné. (GEO2-2020/PU5)

    

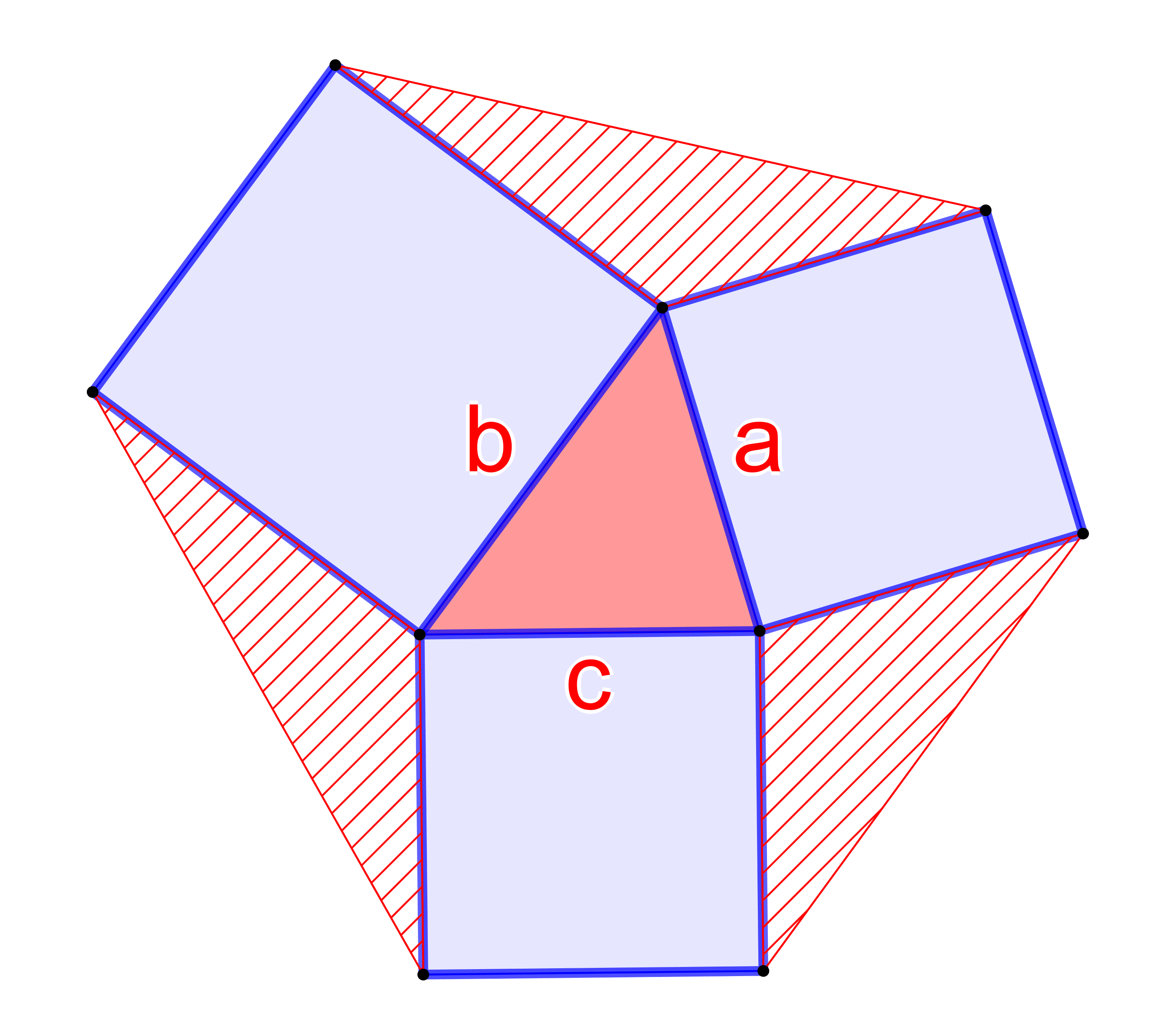
52. Spojíme-li u libovolného trojúhelníku se stranami a, b, c vnější vrcholy čtverců sestrojených nad těmito stranami úsečkami, vzniknou tři trojúhelníky, které jsou na obrázku vyšrafované. Dokažte, že každý z těchto tři trojúhelníků má obsah rovný obsahu výchozího trojúhelníku, tj. červeného trojúhelníku na obrázku. (GEO2-2020/PU6)

    

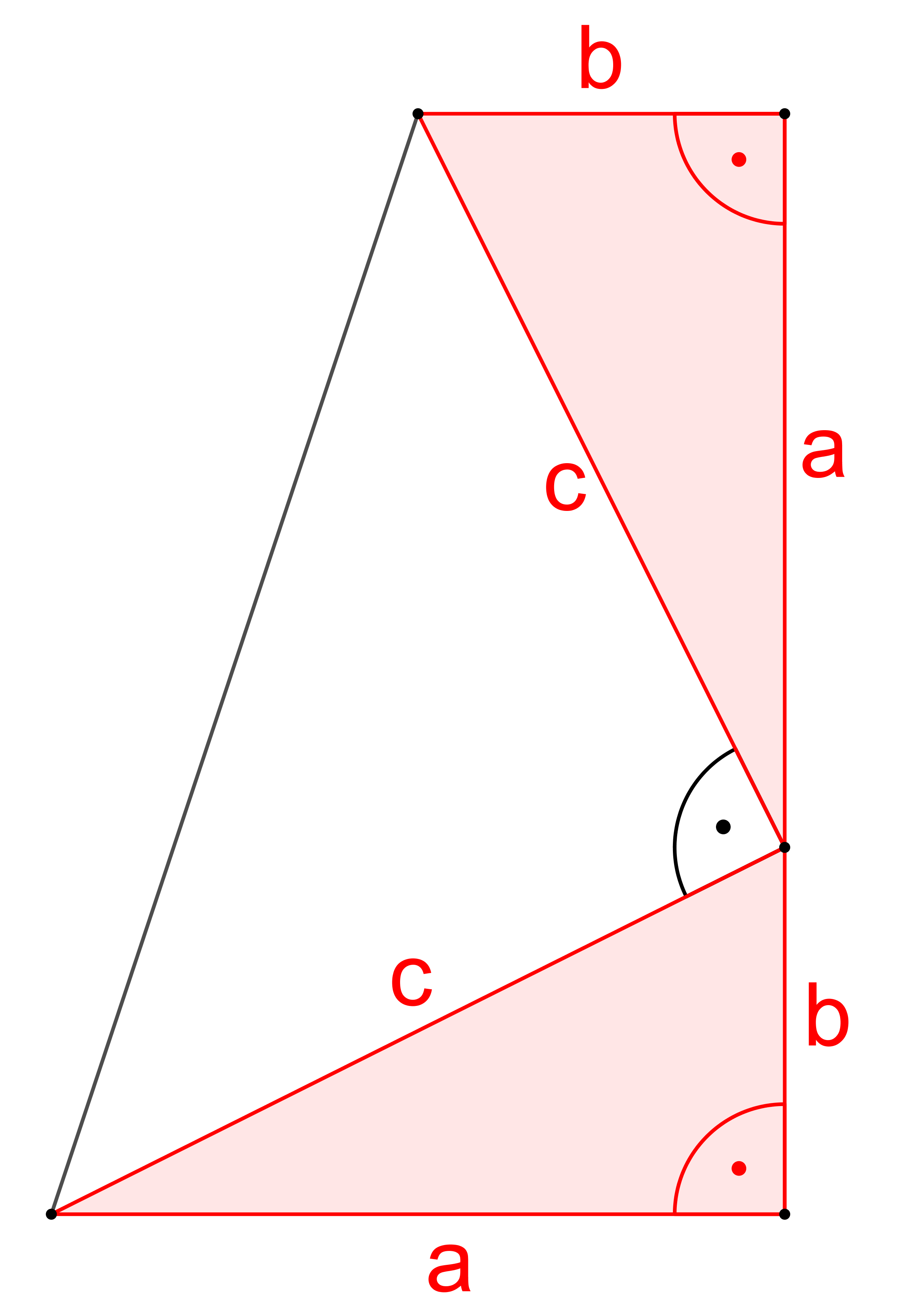
53. Navrhněte způsob, jak využít níže uvedený obrázek k důkazu Pythagorovy věty. (GEO2-2020/PU7)

    

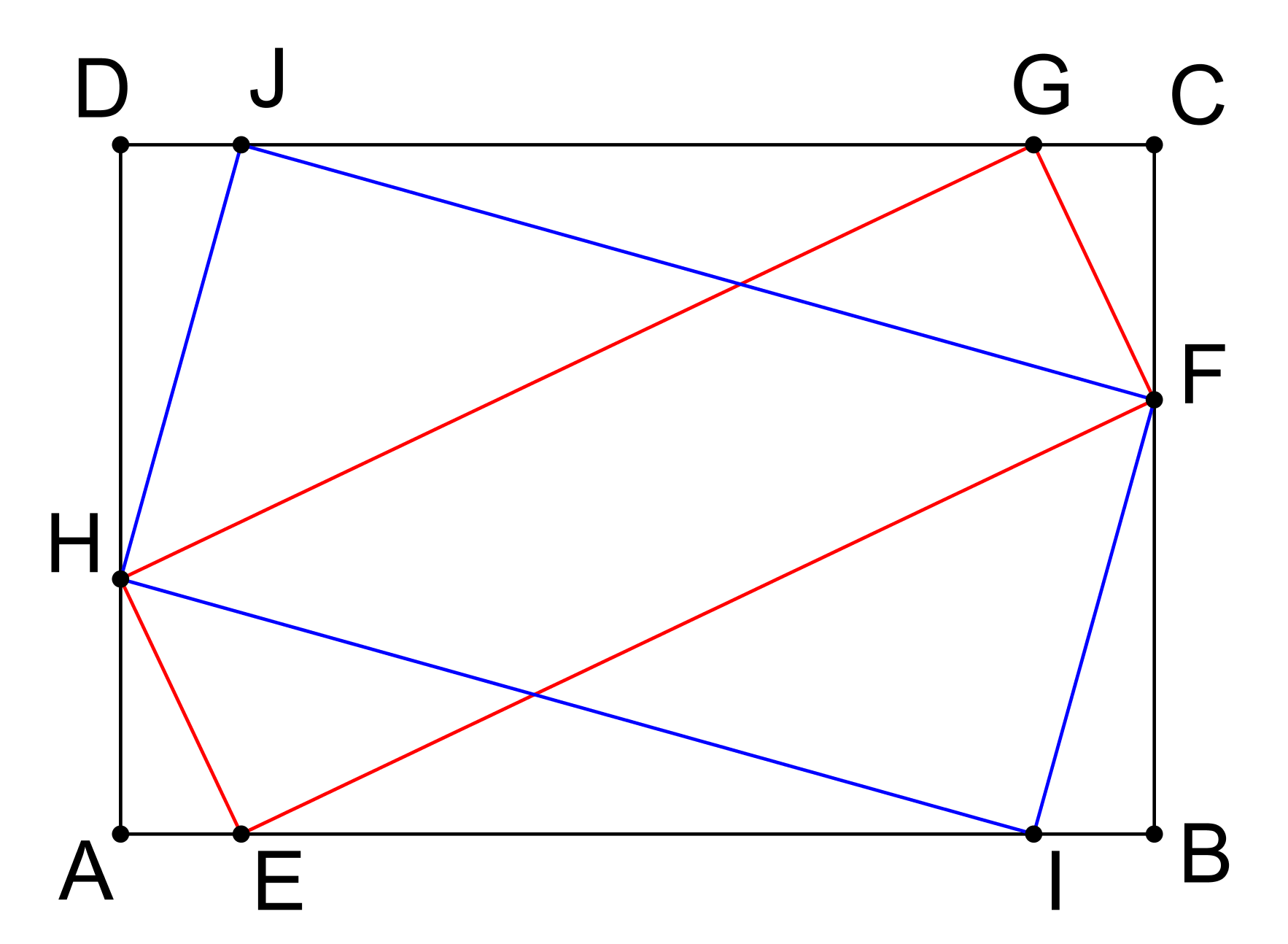
54. Čtyřúhelníky ABCD, EFGH a IFJH na obrázku jsou obdélníky. Dokažte, že součet obsahů EFGH a IFJH je roven obsahu ABCD. (GEO2-2020/PU8)

    

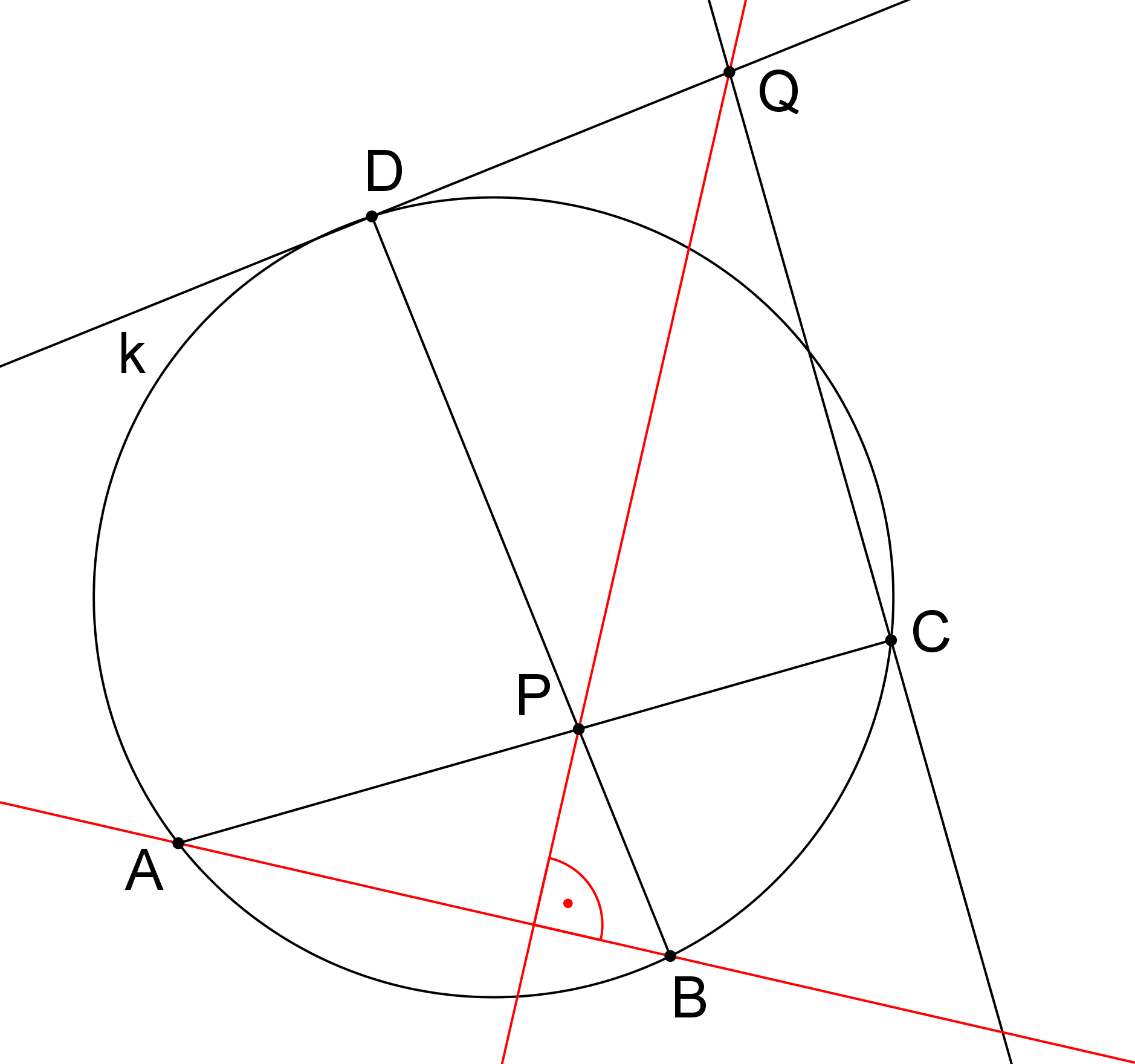
55. Body A, B, C a D leží v uvedeném pořadí na kružnici k, viz obrázek. Tětivy AC a BD se protínají v bodě P, kolmice k AC v bodě C a kolmice k BD v bodě D se protínají v bodě Q. Dokažte, že přímky AB a PQ jsou na sebe kolmé. (GEO2-2020/PU9)

    

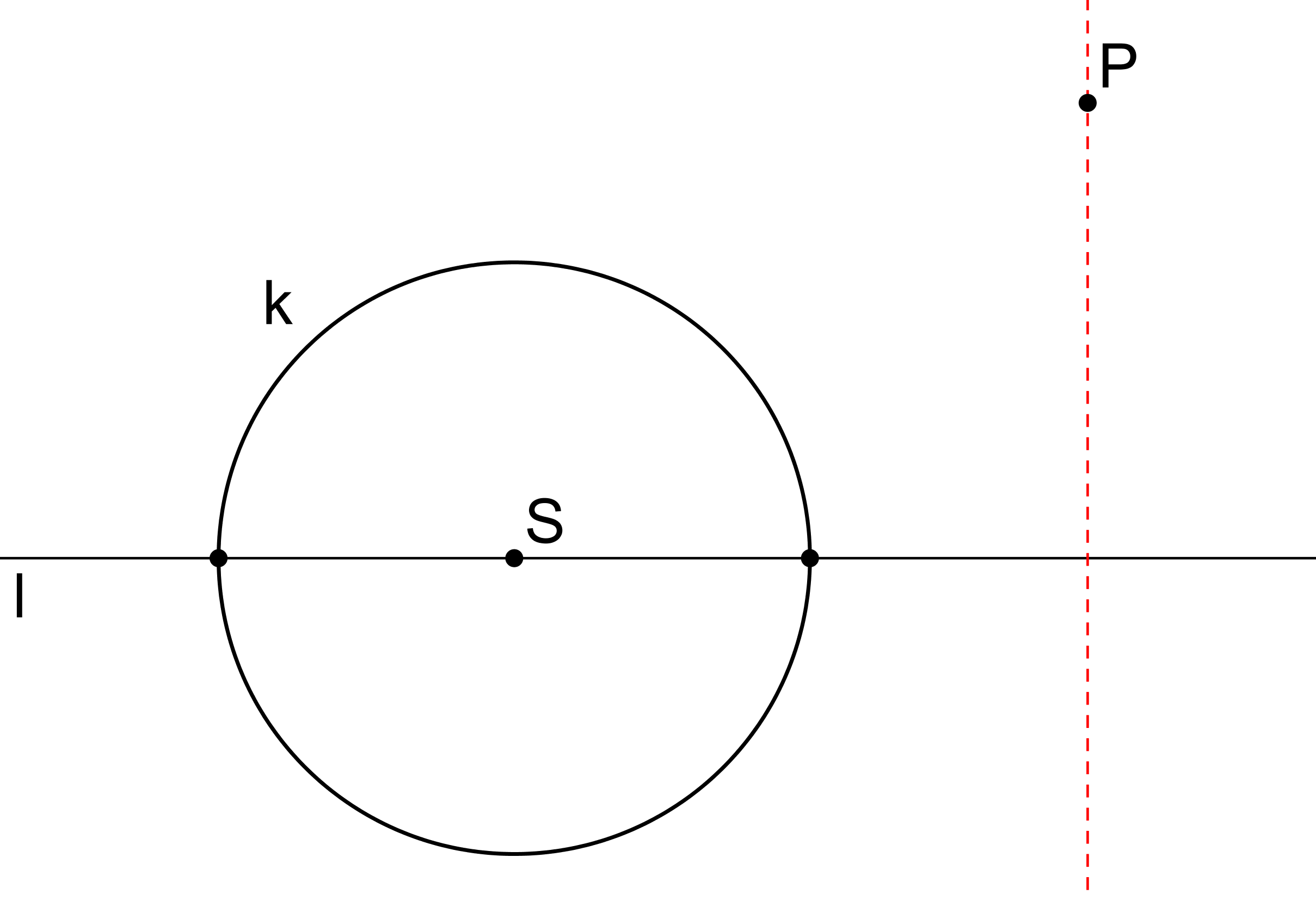
56. Je dána kružnice k se středem S, přímka l jdoucí bodem S a bod P, který neleží na přímce l ani na kružnici k, viz obrázek. Navrhněte postup konstrukce kolmice z bodu P na přímku l pouze použítím pravítka bez měřítka. Správnost navrhnuté konstrukce dokažte. (GEO2-2020/PU10)

    

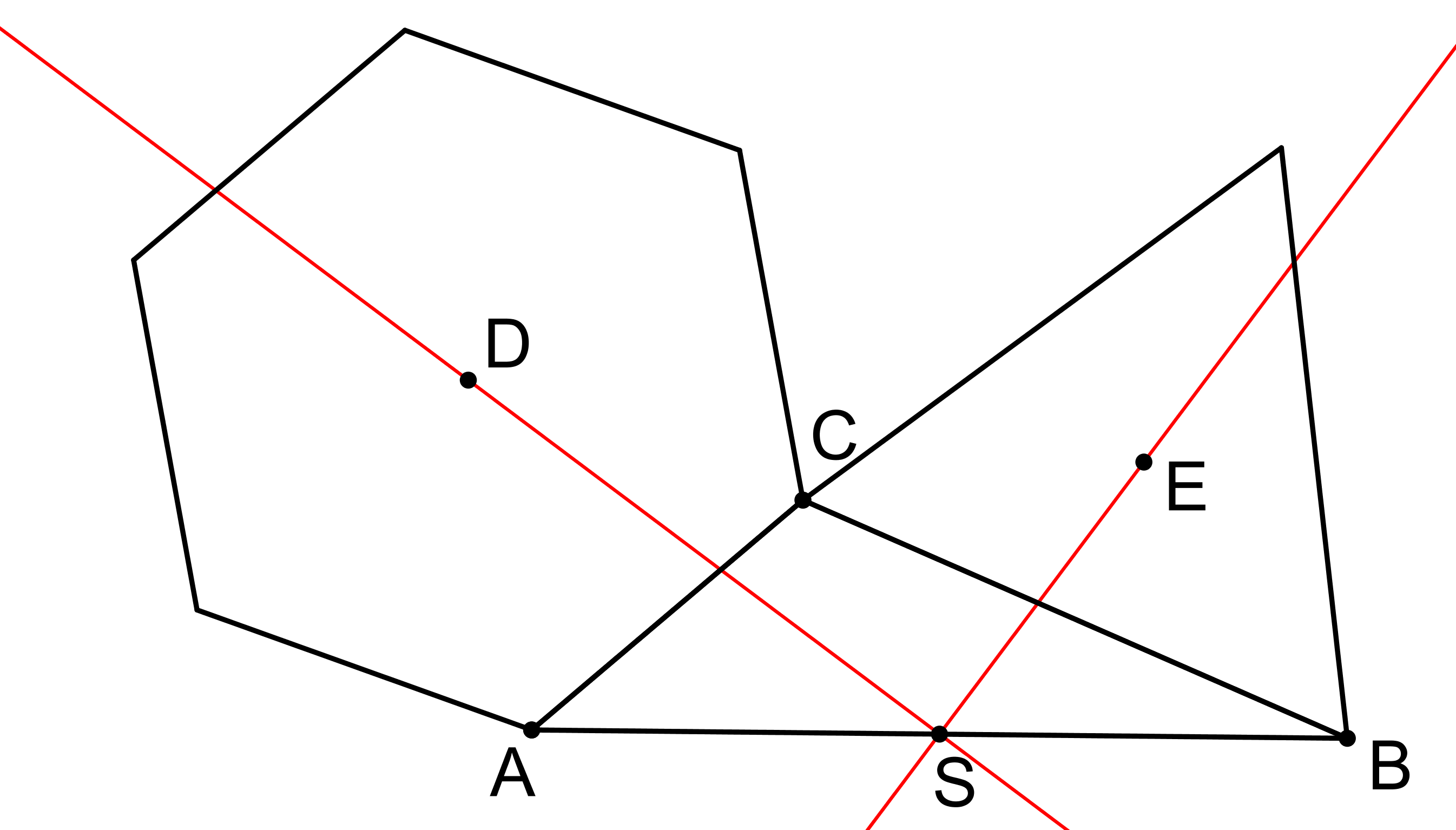
57. Na obrázku je bod D středem pravidelného šestiúhelníku s vrcholem C, který má společný s rovnostranným trojúhelníkem se středem E. Bod S je středem úsečky AB. Dokažte, že úhel ESD je pravý. (GEO2-2020/PU11)

    

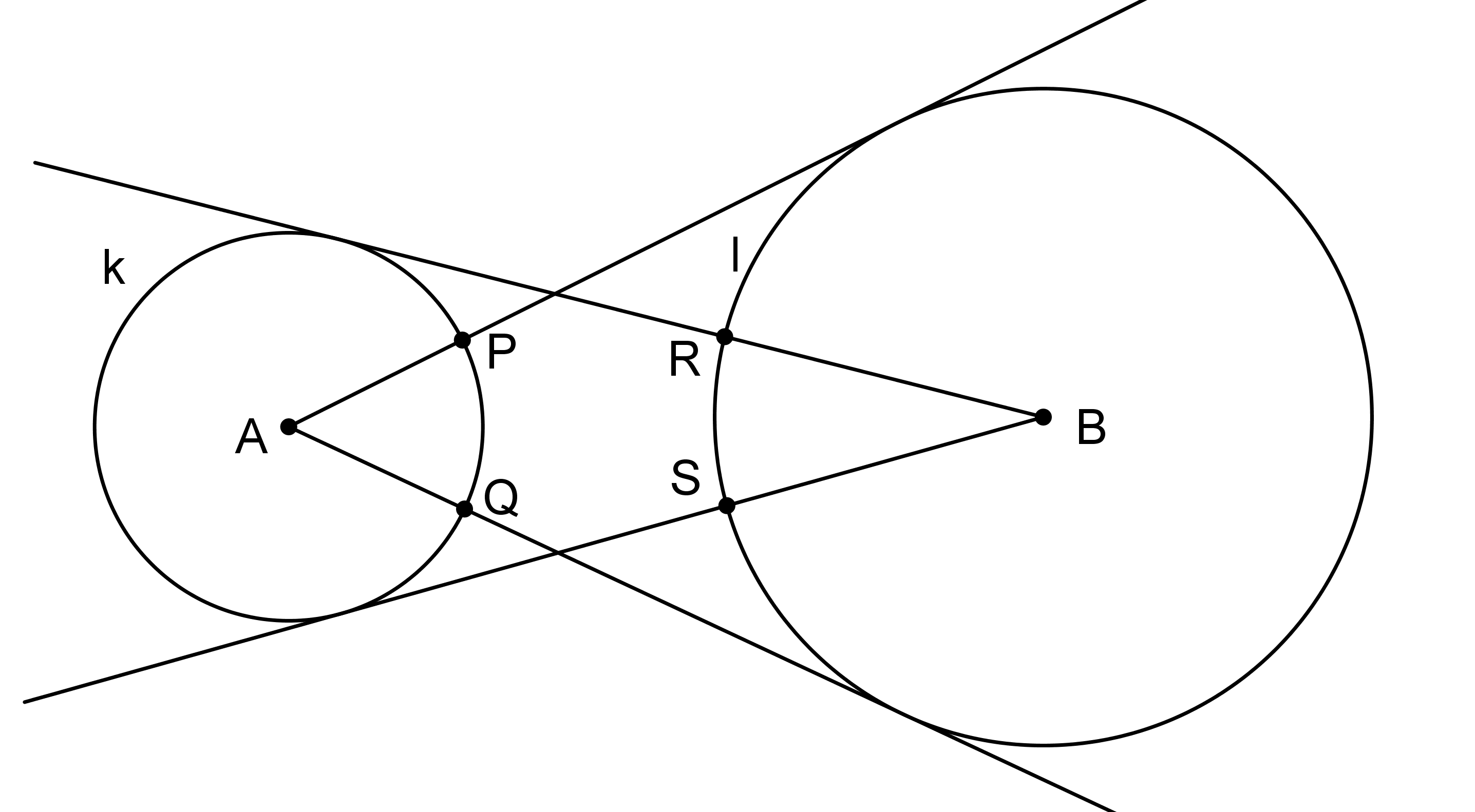
58. Na obrázku jsou dvě kružnice k a l, ze středu každé z nich jsou sestrojeny tečny k té druhé. Přitom tečny z bodu A protínají kružnici k v bodech P, Q a tečny z bodu B protínají kružnici l v bodech R a S. Dokažte, že |PQ|=|RS|. (GEO2-2020/PU12)

    

59. Prémiový úkol č. 1: V rovině je dán trojúhelník ΔABC. Určete všechny body X takové, že úsečky XA, XB a XC mohou být v rovině posunuty, bez otočení či změny délky, tak, že vytvoří trojúhelník.
    [GeoGebra: Ilustrace řešení] Konečný termín možného odevzdání řešení tohoto úkolu posouvám do příštího týdne, tj. do 19. 10. 2021

60. Prémiový úkol č. 2: Navrhněte početní metodu určení, zda daný bod náleží danému trojúhelníku. Metodu demonstrujte na příkladu trojůhelníku ΔABC; A = [-13, -5], B = [5, 2], C = [-6, 10], a bodů K = [-3, 8], M = [-8, -3], P = [-6, 4] a Q = [2, 4].

61. Prémiový úkol č. 3: Kolik trojúhelníků můžeme vepsat pravidelnému n-úhelníku tak, aby jejich vrcholy ležely ve vrcholech n-úhelníku ale jejich strany nebyly totožné s jeho stranami? Například pro pravidelný sedmiúhelník existuje sedm takových trojúhelníků.

    

62. Prémiový úkol č. 4: Je možné libovolnému čtyřstěnu opsat kulovou plochu? Pokud ano, jak najdeme její střed?

63. Prémiový úkol č. 4: Body A = [5, 4, 6], B = [1, 0, 4] jsou sousedními vrcholy krychle ABCDEFGH v trojrozměrném prostoru, jejíž vrchol C leží v rovině xy. Vypočítejte souřadnice zbývajících vrcholů krychle.

64. Prémiový úkol č. 5: Je možné libovolnému čtyřstěnu opsat kulovou plochu? Pokud ano, jak najdeme její střed?

65. Prémiový úkol č. 6: Jaký největší balík ve tvaru kvádru můžete zavázat níže zobrazeným způsobem, pokud máte k dispozici provaz o dělce 12 stop? Spotřebu části délky provazu na vázání uzlů neuvažujeme.

    

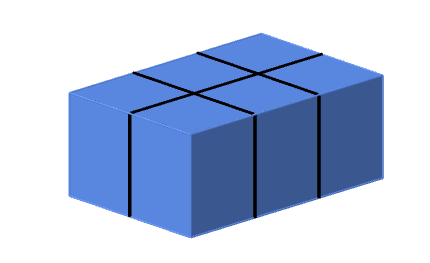
66. Prémiový úkol č. 7: Z určitého počtu jednotkových krychlí je sestavena větší krychle. U té jsou potom nabarveny některé stěny, ne však všechny. Po zaschnutí barvy je velká krychle rozložena zpět na jednotkové krychle. Jejich detailním průzkumem bylo zjištěno, že 218 z nich má na sobě barvu. Jaké byly rozměry velké krychle?

67. Prémiový úkol č. 8:  Určete délku strany největšího čtverce, který lze vepsat do jednotkové krychle. Jinak řečeno, jaký největší pevný čtverec můžete vložit do krychlové krabice o délce hrany 1 m?

    

68. Prémiový úkol č. 9: Dokažte, že pro trojboký jehlan A, B, C, D, který vznikne "uříznutím" z kvádru dle obrázku, platí

    S²_ABC=S²_ABD+S²_BCD+S²_ACD,
    kde S_ABC, S_ABD, S_BCD, S_ACD jsou obsahy stěn tohoto jehlanu.

69. Prémiový úkol č. 10:  Mezi dvěma budovami jsou postaveny žebříky různých dělek a, b, viz obrázek. Najděte vztah pro výpočet vzdálenosti budov x, znáte-li ještě výšku c, v níž se žebříky kříží.

    

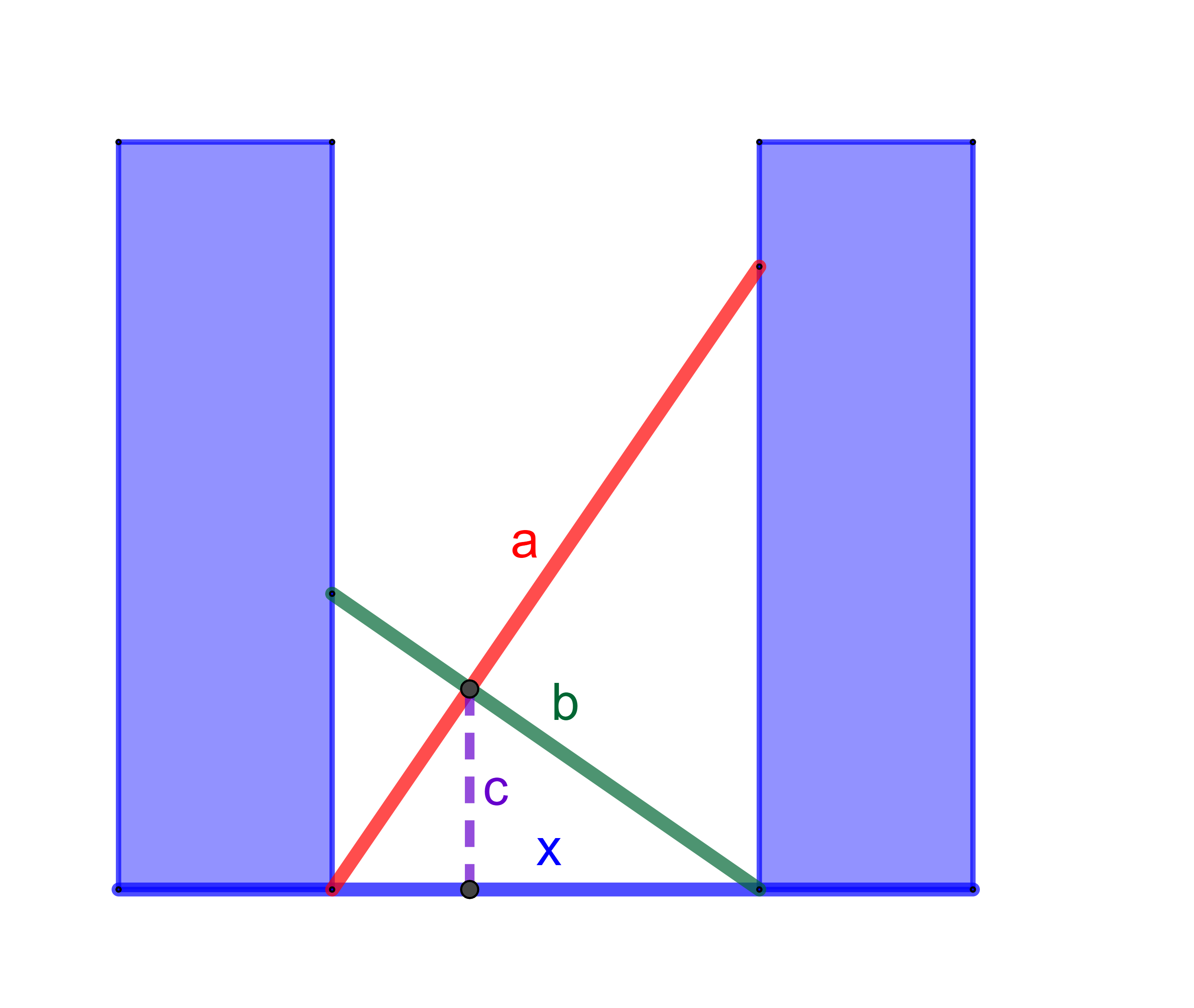
70. Prémiový úkol č. 11:  U libovolného trojúhelníku se stranami a, b, c označme k, l, m úsečky spojující vnější vrcholy čtverců sestrojených nad těmito stranami, viz obrázek. Dokažte, že platí

    k²+l²+m²=3(a²+b²+c²).

71. Prémiový úkol č. 12:  Čtyři kružnice k, l, m, n jsou uspořádány do uzavřeného řetězu, v němž mají každé dvě sousední kružnice vždy jeden společný bod, viz obrázek. Dokažte, že tyto body dotyku A, B, C, D leží (pro každé takové uspořádání čtyř kružnic) na společné kružnici. (PLA-2018/PU11)

    

72. Prémiový úkol č. 13: Do půlkruhu s poloměrem 4 jsou vepsány dva kruhy s průměry 4 a d, které se dotýkají, viz obrázek. Vypočtěte d.