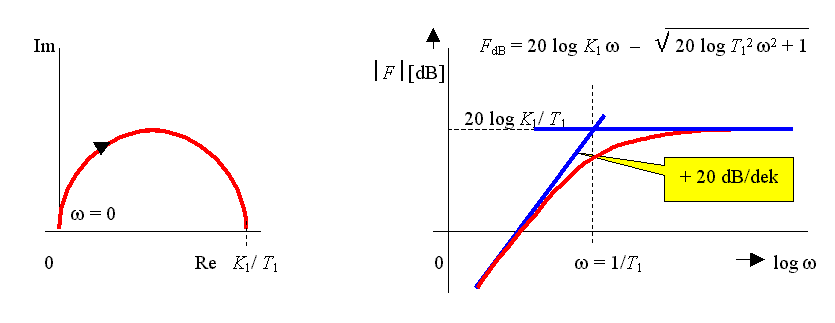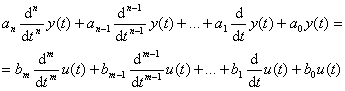
4. Základní typové dynamické články
Některé typické dynamické vlastnosti regulačních obvodů se nechají demonstrovat na zařízeních, jejichž diferenciální rovnice jsou maximálně druhého řádu, takže jsou snadno řešitelné. Takovéto zařízení se pak nazývají typové dynamické články. Jsou jakýmsi normálem základních druhů dynamických vlastností. Pro základní druhy dynamických vlastností nabývá diferenciální rovnice
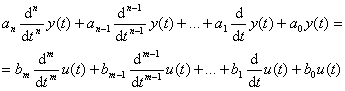
specifických tvarů a podle toho se rozeznávají tři základní druhy dynamických vlastností systémů:
a) statické systémy
b) astatické (integrační) systémy
c) derivační systémy
4.1. Statické systémy
Statické systémy mají tvar diferenciální rovnice
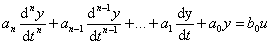
Jsou charakterizovány tím, že diferenciální rovnice má na levé straně (n + 1) členů. Při přivedení vstupní veličiny jednotkového skoku ustálí se výstupní veličina na konstantní hodnotě:

4.1.1. Statický člen nultého řádu (člen proporcionální -P)
Příklady provedení:
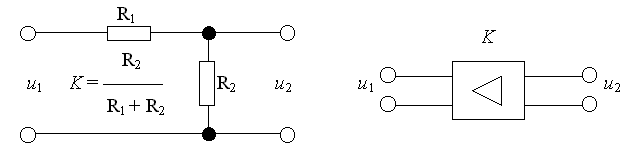
Diferenciální rovnice:

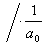
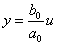
 -
zesilovací konstanta
-
zesilovací konstanta
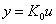
Operátorový přenos:
a0 y = b0 u po transformaci ® a0 Y (p) = b0U(p)

Přechodová charakteristika (odezva na jednotkový vstupní skok):
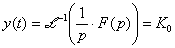

Frekvenční charakteristika:
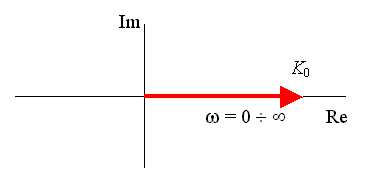
a) v komplexní rovině: F (jw) = K0 frekvenční přenos je nezávislý na frekvenci, jeho modul je konstantní, argument rovný nule.
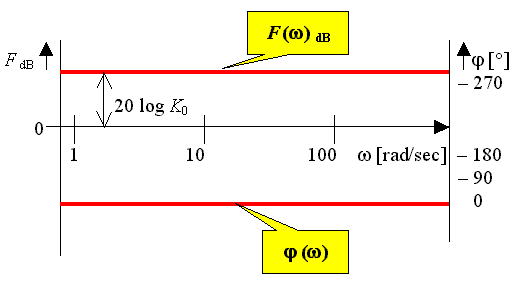
b) v logaritmických souřadnicích: ô F (jw) ôdB = 20 log K0 , j (w) = 0
4.1.2. Statický člen prvního řádu (setrvačný člen), (proporcionální člen se zpožděním prvního řádu)
Příklady provedení:

Diferenciální rovnice:

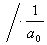

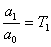 -
setrvačná časová konstanta [ s ]
-
setrvačná časová konstanta [ s ]
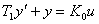
Operátorový přenos:
Za předpokladu nulových počátečních podmínek po Laplaceově transformaci:
a1 p Y (p) + a0 Y (p) = b0 U (p)
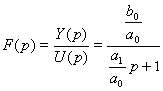
p = c + jw - komplexní proměnná, má rozměr frekvence [s-1]
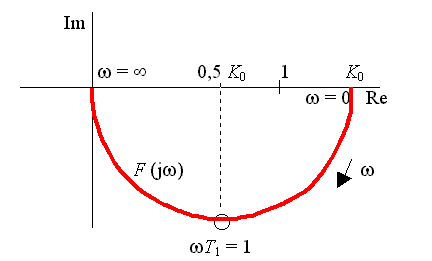
Typový tvar přenosové funkce: 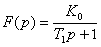
Přechodová charakteristika:
 - jednotkový skok
- jednotkový skok

Po zpětné transformaci:

K0 = y (Ą )
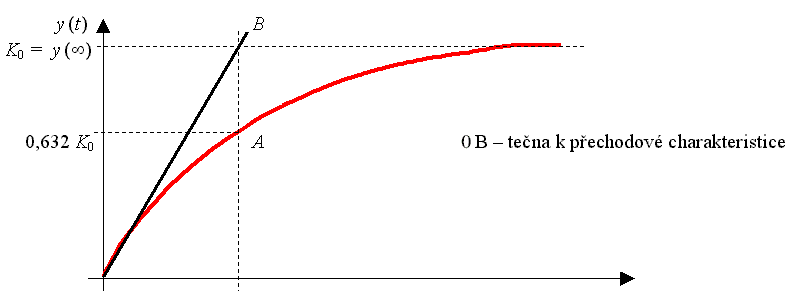
Frekvenční charakteristika:
a) v komplexní rovině:
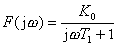


b) v logaritmických souřadnicích:
Pro amplitudovou frekvenční charakteristiku platí:
Protože výraz 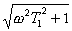 nelze obecně logaritmovat,
nelze obecně logaritmovat,
Pro  je
je 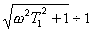 zjednodušuje se zanedbáním:
zjednodušuje se zanedbáním:
a ôF (jw)ôdB = 20 log K0
Pro  je
je 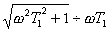
a ôF (jw)ôdB = 20 log K0 - 20 log w T1
Mezní případ mezi 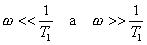 je
je 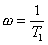
Od w = 0 do 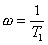 je amplitudová frekvenční charakteristika
přibližně dána polopřímkou (asymptotou) vodorovnou s osou 0 dB a vzdálenou od
ní 20 log K0.
je amplitudová frekvenční charakteristika
přibližně dána polopřímkou (asymptotou) vodorovnou s osou 0 dB a vzdálenou od
ní 20 log K0.
Od  do w = Ą je amplitudová
frekvenční charakteristika přibližně dána polopřímkou (asymptotou) klesající o
20 dB na dekádu (desetinásobek) frekvence. Průběh fáze je dán vztahem
j = - arctg wT1 Pro
w ® 0 je j ® 0 , pro w ®
Ą je j ® - 90°, pro
do w = Ą je amplitudová
frekvenční charakteristika přibližně dána polopřímkou (asymptotou) klesající o
20 dB na dekádu (desetinásobek) frekvence. Průběh fáze je dán vztahem
j = - arctg wT1 Pro
w ® 0 je j ® 0 , pro w ®
Ą je j ® - 90°, pro 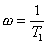 je j
= - 45°
je j
= - 45°
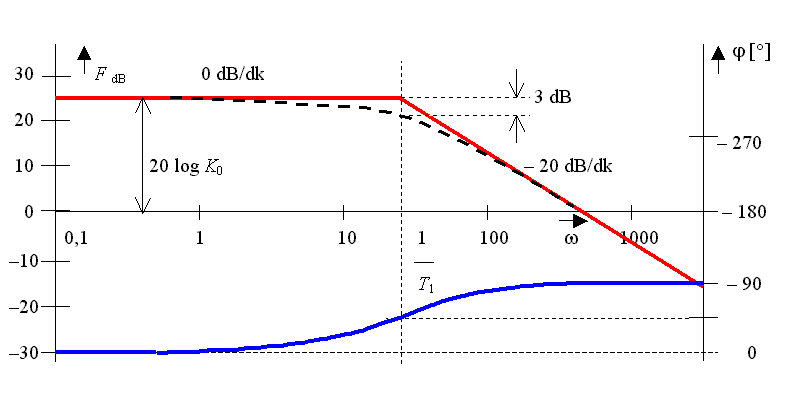
Nahrazení amplitudové frekvenční charakteristiky asymptotami je tím přesnější,
čím jsou hodnoty w více vzdáleny od hodnoty  . Největší
chyba vzniká pro
. Největší
chyba vzniká pro 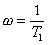 . Její velikost se zjistí dosazením
. Její velikost se zjistí dosazením
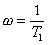 do vztahu:
do vztahu:
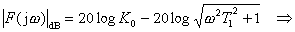

Ţ Skutečný průběh amplitudové charakteristiky leží tedy ve zlomu asymptot o 3 dB níže než udávají asymptoty.
Dynamické vlastnosti respektované statickým členem 1. řádu mají zařízení, která obsahují jednu energetickou kapacitu (tj. prvek schopný akumulovat v sobě energii).
4.1.3. Statický člen druhého řádu
Příklady provedení:
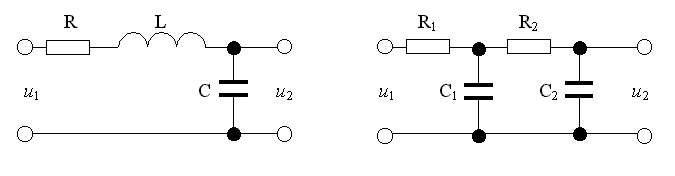
Diferenciální rovnice:
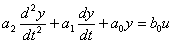
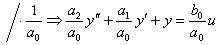


Pokud se položí: T2 = T , T1 = 2 x T , pak diferenciální rovnice přejde ve tvar:
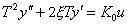 , kde T je časová
konstanta a
, kde T je časová
konstanta a  je poměr tlumení.
je poměr tlumení.

Operátorový přenos:
Po Laplaceově transformaci:
Y (p) · (a2 p2 + a1 p + a0 ) = b0 U(p)
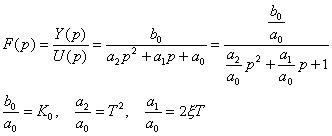
Typový tvar přenosové funkce:
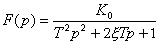
Pokud položíme  , pak
, pak 
Přechodová charakteristika:
Pro jednotkový skok platí:
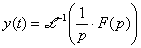
Pro průběh přechodové charakteristiky jsou rozhodující kořeny jmenovatele přenosu F (p).
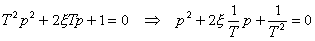
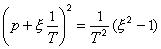
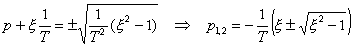
Vzhledem k velikosti x mohou nastat tyto případy:
a) x > 1
p1 = 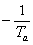 ,
p2 =
,
p2 = 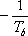 2
reálné, různé, záporné kořeny
2
reálné, různé, záporné kořeny
přičemž 
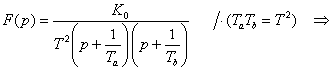

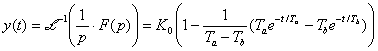
Přechodová charakteristika je aperiodická přetlumená:
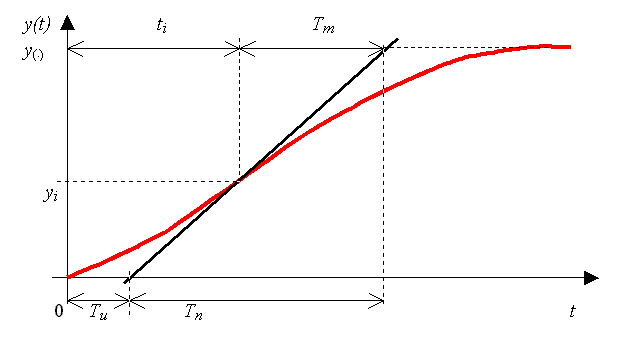
b) x = 1
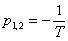 2
reálné, stejné, záporné kořeny
2
reálné, stejné, záporné kořeny
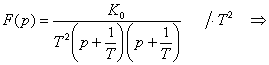
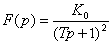
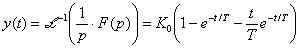
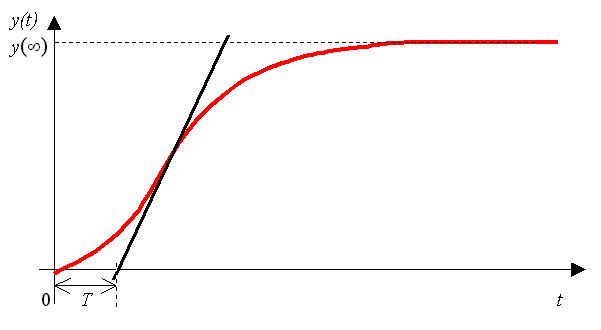
Přechodová charakteristika je na mezi aperiodicity:
c) 0 < x < 1
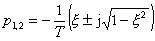
Ţ 2 komplexně sdružené kořeny se zápornou reálnou
částí. Výraz 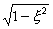 je
reálné číslo
je
reálné číslo
Přechodová charakteristika je kmitavá tlumená (tlumené harmonické kmity):
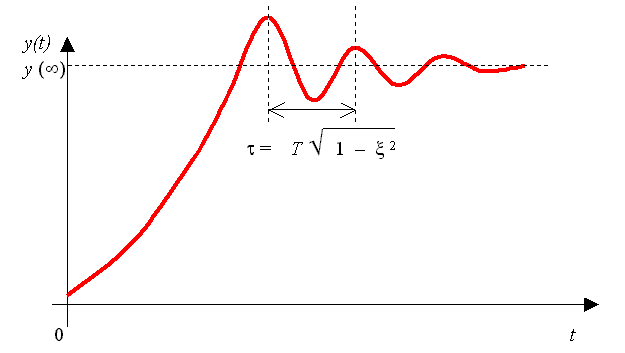
Kmity probíhají s frekvencí wv , která se nazývá vlastní frekvencí kmitavého článku.
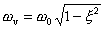 w0
= přirozená frekvence článku (frekvence vlastních kmitů bez tlumení).
w0
= přirozená frekvence článku (frekvence vlastních kmitů bez tlumení).
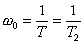 Činitel tlumení:
Činitel tlumení:


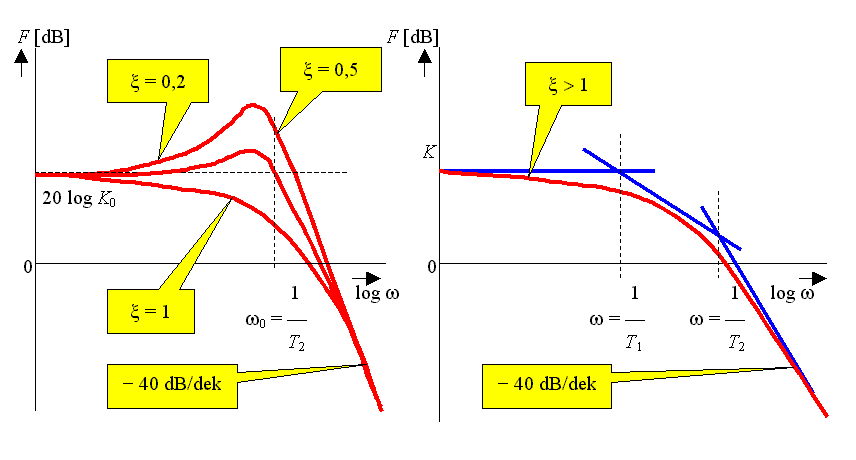
Frekvenční charakteristika:
a) v komplexní rovině:

b) v logaritmických souřadnicích:
4.1.4. Zpožďující členy vyšších řádů
Diferenciální rovnice má tvar:
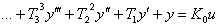
Operátorový přenos:

Pokud mnohočlenu ve jmenovateli odpovídají reálné kořeny je možné napsat přenos ve tvaru:
 ,
,
kde T1 = Ta + Tb + Tc ; T22 = Ta Tb + Tb Tc + Tc Ta ; T33 = Ta · Tb · Tc
Z tohoto vyjádření je patrno, že výsledný přenos je dán součinem dílčích přenosů typu
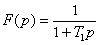 , násobený K0
, násobený K0
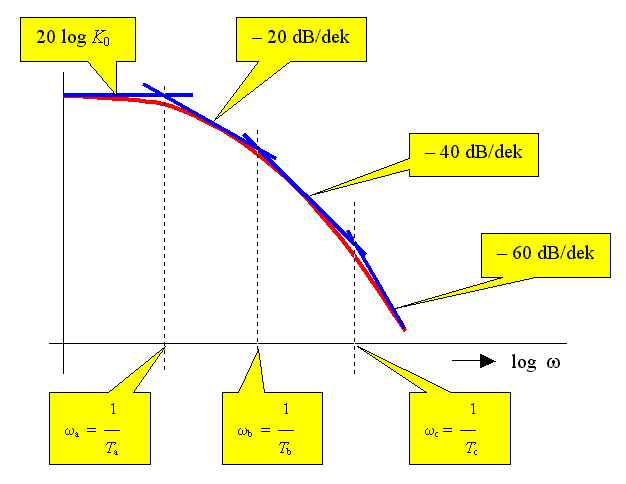
Výsledná frekvenční charakteristika je tedy dána součinem frekvenčních charakteristik zpožďujících členů prvého řádu, která každá leží celá v jednom kvadrantu. Frekvenční charakteristika dvou v sérii zapojených zpožďujících členů prvého řádu musí potom procházet dvěma kvadranty.
Výslednou logaritmickou frekvenční charakteristiku je možno sestrojit sečtením frekvenčních charakteristik jednotlivých dílčích přenosů.
4.2. Astatické (integrační) systémy
Astatické systémy mají tvar diferenciální rovnice
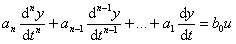
Jsou charakterizovány tím, že diferenciální rovnici na levé straně chybí prostý člen a na pravé straně je pouze prostý člen.
Při přivedení vstupní veličiny jednotkového skoku, mění se výstupní veličina po skončení přechodového děje
rovnoměrným pohybem rychlostí 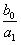 , tedy vstupní veličinu integruje.
, tedy vstupní veličinu integruje.
4.2.1. Ideální integrační člen
Diferenciální rovnice: 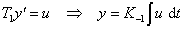
Operátorový přenos: 
Přechodová charakteristika: 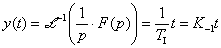

Frekvenční charakteristika: Frekvenční charakteristika v log. souř.:
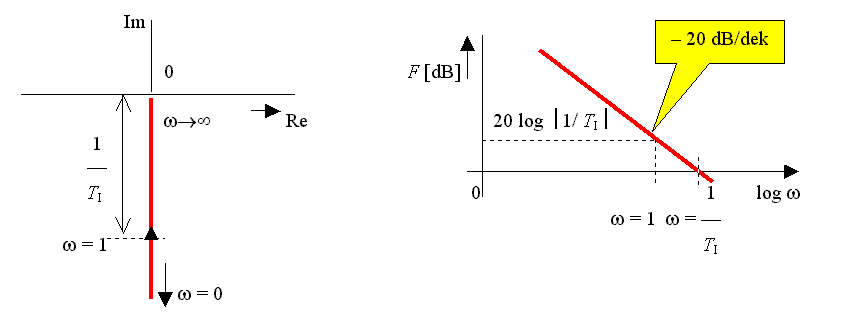
4.2.2. Integrační člen se zpožděním 1.řádu
Příklad provedení:

Vstupem je napájecí signál a výstupem dráha (úhel natočení).
Časová konstanta 
J = moment setrvačnosti
B = konstanta tlumení motoru
Diferenciální rovnice:

Operátorový přenos:
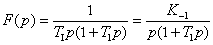
Přechodová charakteristika:
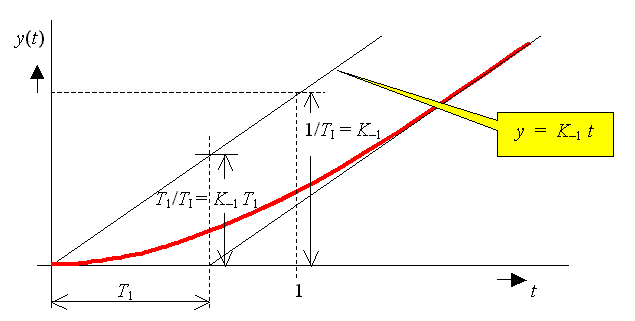
Frekvenční charakteristika: Frekvenční charakteristika v log. souř.:
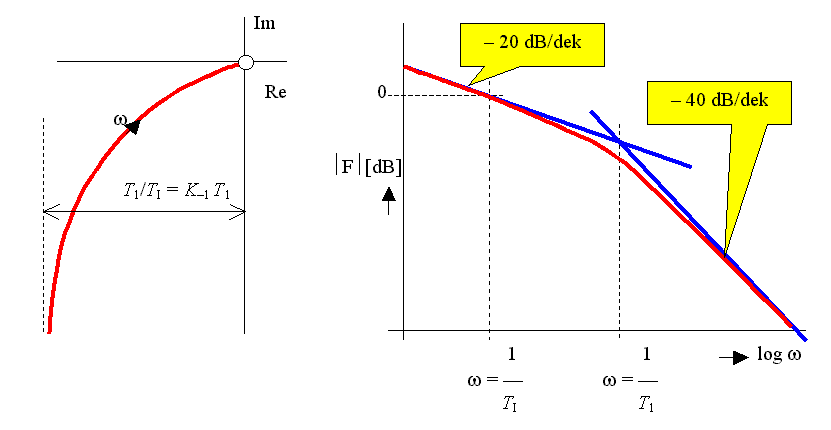
4.3. Derivační systémy
Derivační systémy mají tvar diferenciální rovnice

Jsou charakterizovány tím, že diferenciální rovnici na pravé straně chybí prostý člen. Při přivedení vstupní veličiny jednotkového skoku, ustálí se výstupní veličina po skončení přechodového děje na nule.
Derivace daného signálu v nějakém okamžiku nám dává informaci o tom, jak bude tento signál přibližně pokračovat v nejbližším následujícím okamžiku.
4.3.1. Ideální derivační člen
Příklad provedení:
Tachodynamo
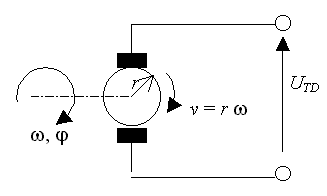
Malé dynamo s permanentním magnetem ve statoru, jehož napětí je přímo úměrné úhlové rychlosti podle vztahu E = B l v
E = indukovaná elektromotor. síla
B = magnetická indukce mezi póly statoru - konstanta
l = aktivní délka vodičů kotvy - konstanta
v = r w = obvodová rychlost vodičů kotvy
w = úhlová rychlost.
Platí UTD = KTD • w
Pokud se považuje za vstupní veličinu úhel natočení j, pak je napětí tachodynama

Diferenciální rovnice: 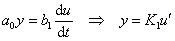 ,
kde F (p) = K1 p
,
kde F (p) = K1 p
Operátorový přenos: 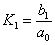
Přechodová charakteristika:
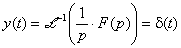 - Diracův impuls
- Diracův impuls
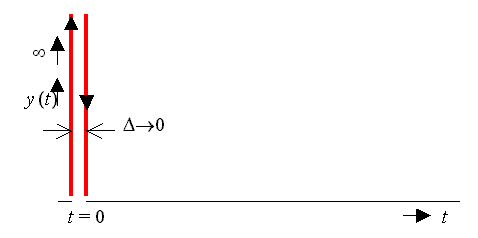
Frekvenční charakteristika: Frekvenční charakteristika v log. souř.:
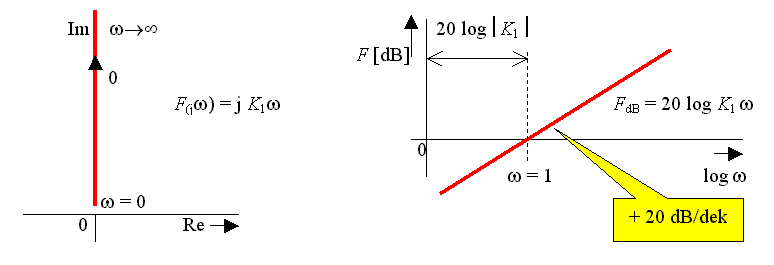
4.3.2. Derivační člen se zpožděním 1. řádu

Diferenciální rovnice:  , kde
, kde
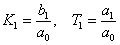
Operátorový přenos: 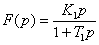
Přechodová charakteristika:
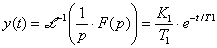
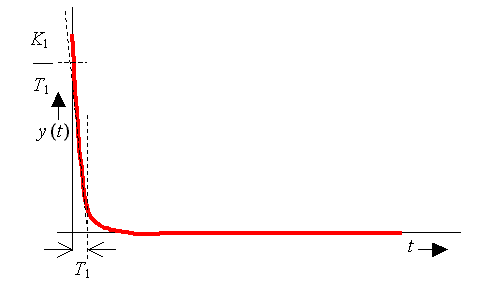
Frekvenční charakteristika: Frekvenční charakteristika v log. souř.: