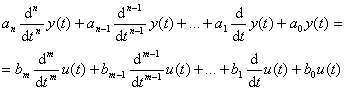
5. Členy s dopravním zpožděním

Jestliže se vstupní veličina začíná měnit se zpožděním t (tj. její změna započne v čase t = t), přičemž průběh vstupní veličiny se počítá od t = 0, má příslušný člen dopravní zpoždění a jeho obecná diferenciální rovnice vyjádřená původně ve tvaru

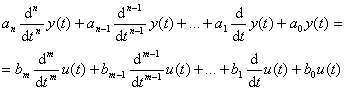
se změní. Příčinou dopravního zpoždění t může být např. konečná rychlost šíření signálu na dlouhé spojovací cestě, pokud se tato cesta zahrne do dynamických vlastností příslušného členu.

Diferenciální rovnice:

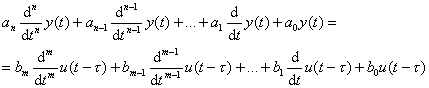
Operátorový přenos:

Operátorový přenos členu s dopravním zpožděním t se získá tak, že operátorový přenos stejného členu bez dopravního zpoždění se násobí činitelem e ^{- pt} .

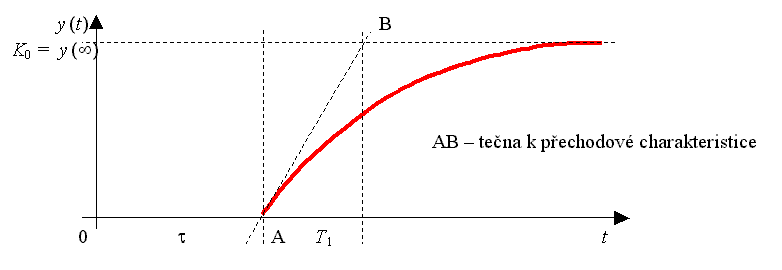
Přechodová charakteristika:

Má průběh stejný jako u členu bez dopravního zpoždění, avšak nezačíná v t = 0 nýbrž až v t = t.

Např. statický člen 1. řádu má operátorový přenos a tento člen s dopravním zpožděním

operátorový přenos 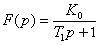a tento člen s dopravním zpožděním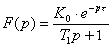

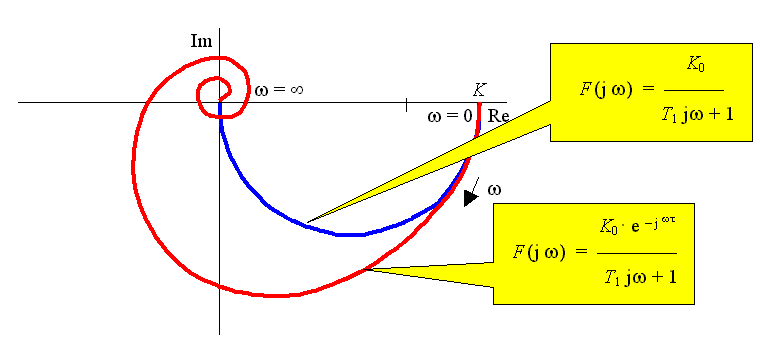
Frekvenční charakteristika:

Po dosazení p = j w do operátorového přenosu bude se přenos lišit od přenosu členu bez dopravního zpoždění jenom činitelem e ^{- j wt} . Tento činitel vyjadřuje pouze fázový posun o úhel - wt . Amplituda zůstává stejná jako u členu bez dopravního zpoždění, ale fáze se mění od 0 do - Ą při změně w od 0 do Ą a vytváří spirálu kolem počátku (oproti členu bez dopravního zpoždění, kde se fáze mění od 0 do - 90 °).