DVPP: DESKRIPTIVNÍ GEOMETRIE I - KMA/DG1ZŽ

Deskriptivní geometrie se věnuje zkoumání geometrických vztahů trojrozměrných objektů prostřednictvím jejich dvojrozměrného znázornění.
Její studium nám tak zprostředkovává poznání a pochopení stereometrických vztahů, učí nás, jak správně interpretovat dvojrozměrné pohledy na tyto vztahy a také významně kultivuje naši schopnost prostorové vztahy graficky vyjádřit způsobem každému srozumitelným.

V předmětu Deskriptivní geometrie I byste se měli naučit správně chápat vztahy mezi prostorovými útvary, tyto vztahy vhodně zvoleným způsobem znázorňovat a nebo naopak, takováto znázornění zpětně správně interpretovat. Získáte tak schopnost komunikovat se svým okolím o trojrozměrných objektech a jejich vztazích.

Osnova předmětu

• Úvod do deskriptivní geometrie.
• Eukleidovský trojrozměrný prostor. Souřadnice bodu. Promítání. Tři základní průměty.
  
  

  PŘEDNÁŠKA 1 Úvod do deskriptivní geometrie. Testy prostorových schopností (orientace v prostoru, tvorba prostorových představ a manipulace s nimi): Santa Barbara Solids Test (http://spatiallearning.org/index.php/testsainstruments) Purdue Visualization of Rotations Test (http://www.quiz.biz/quizz-250841.html)

• Volné rovnoběžné promítání.
  
  
• Zobrazování prostorových útvarů. Přehled základních promítacích metod: Kótované promítání. Mongeovo promítání.
• Přehled základních promítacích metod: Kosoúhlé promítání. Axonometrie. Volné rovnoběžné promítání.
  
  
  

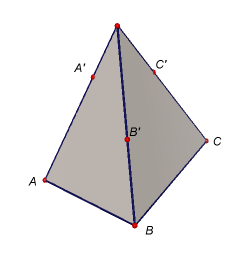
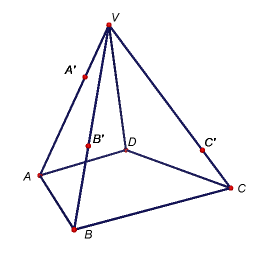
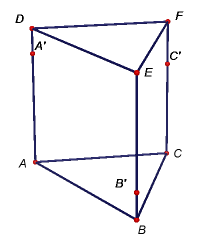
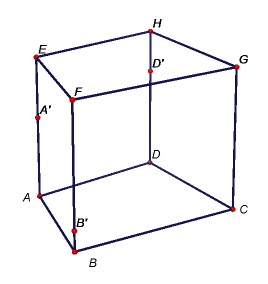
  PŘEDNÁŠKA 2 Úvod do středové kolineace a osové afinity / Středová kolineace / Osová afinita GeoGebra: [Středové promítání] [Středová kolineace] [Rovnoběžné promítání] [Osová afinita] Úkol 1:  V programu GeoGebra 5 vytvořte modely těles dle níže uvedených obrázků i s popisem zobrazených bodů. Potom sestrojte řezy těchto těles rovinami určenými body A'B'C', resp. A'B'D'. Úkol 2:  Osová afinita v rovině je dána osou o a dvojicí bodů P, P'. Sestrojte obraz daného trojúhelníku ABC. [Zadání v GeoGebře] Příklad: Je dána přímka o a trojúhelník ABC. Sestrojte obraz A'B'C' trojúhelníku ABC v takové osové afinitě, aby byl trojúhelník A'B'C' rovnostranný. [Řešení v GeoGebře] Úkol 3:  Sestrojte řez kvádru ABCDA'B'C'D' rovinou MNP; M je vnitřní bod hrany CC', pro který platí 4|CM|=|CC'|, N je střed hrany A'D' a bod P leží na prodloužení hrany B'B za bod B a platí 3|BP|=|BB'|. (J. Polák: Přehled středoškolské matematiky, str. 481, Zadání v GeoGebře)

  
  
  

  PŘEDNÁŠKA 3 Vybrané metody promítání. Úkol 1: V axonometrii, která je zadána axonometrickým trojúhelníkem XYZ o stranách x=5, y=4 a z=5 sestrojte axonometrický průmět bodu A o souřadnicích A[3,5,6] spolu s jeho souřadnicovým kvádrem. [Animace řešení] Úkol 2: V kosoúhlém promítání, které je dáno úhlem zkosení ω = 145° a poměrem zkreslení q=1/2, zobrazte kosoúhlý průmět bodu A o souřadnicích A[3,5,6] spolu s jeho souřadnicovým kvádrem. [Animace řešení] Úkol 3 (domácí):  Zobrazte kvádr o rozměrech 3, 4 a 5 cm prostřednictvím těchto zobrazovacích metod: a) Volné rovnoběžné promítání. b) Kosoúhlé promítání (ω = 150°, 3/4). c) Kavalírní perspektiva (ω = 135°). d) Vojenská perspektiva (ω = 135°). (Dle vlastního uvážení zvolte pravotočivou nebo levotočivou soustavu souřadnic. Rýsujte!)

• Rekonstrukce prostorového objektu ze základních průmětů.
• Kótované promítání. Zobrazení bodu, přímky a roviny. Vybrané polohové úlohy.
  
  

  PŘEDNÁŠKA 4 Kótované promítání: Zobrazení bodu, přímky a úsečky. Úkol 1:  Určete délku úsečky AB; A[-4;2;5], B[2;-2;1]. [3D znázornění (GeoGebra), Animace řešení, varianta 1, Animace řešení, varianta 2] Úkol 2: V kótovaném promítání jsou dány průměty bodů A, B; |A1B1| = 7 cm, zA=5, zB=2. Určete: a) Stopník přímky AB. b) Odchylku α přímky AB od průmětny. c) Skutečnou velikost úsečky AB. d) Vystupňujte přímku AB. [Zadání v PDF] Úkol 3: Rozhodněte o vzájemné poloze přímek p = AB, q = CD (viz prezentace k přednášce): [Animace / varianta 1 , Animace / varianta 2]

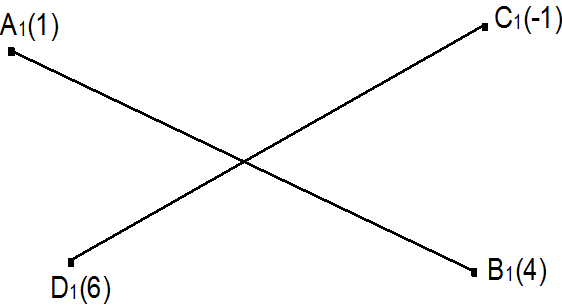
• Kótované promítání. Vybrané polohové úlohy. Aplikace.
  
  

  PŘEDNÁŠKA 5 Zobrazení roviny. Úkol 4: Určete stopu a hlavní přímky roviny ρ=ABC; A=[2,5;3,5;1,5], B=[7;2,5;0,8], C=[5;6,5;4]. Sestrojte odchylku roviny ρ od průmětny. Úkol 5: Určete velikost úhlu ACB (zobrazení trojúhelníku ABC ve skutečné velikosti). [Animace] Úkol 6: Zobrazení čtverce ABCD ve skutečné velikosti. [Animace] Úkol 7: V rovině ρ(6;7;4,5) zobrazte čtverec ABCD s úhlopříčkou AC, A[4;1;?], C[2;3;?]. Úkol 8: (Průsečnice dvou rovin)   Sestrojte průsečnici rovin α=(5,5,5), β=(-6,4,2).  [Animace] Vzájemná poloha přímky a roviny. Úkol 9: (Průsečík přímky s rovinou)   Zobrazte průsečík přímky a=AB s rovinou ρ, která je dána spádovou přímkou s=LM; A=[2;2;1], B=[-5;2;4], L=[-3;4;0], M=[3;1;5].  [Animace] Úkol 10: Zobrazte průsečík přímky a s rovinou ρ: a) a = AB; A = [1;2;-2], B = [1;2;3], ρ = (-5;6;3), b) a = PA; P = [-4;0,5;0], A = [3;2;6], ρ = (3;4;∞), c) a = AB; A = [4;1;5], B = [-2;5;-1], ρ = (∞;∞;3), d) a = PA; P = [0;4;0], A = [1,5;0;8], ρ = (5;7;4) [Animace]. Úkol 11:  Určete vzdálenost bodu C od přímky a = AB: A = [-5; 0; 2], B = [0; 4; 0], C = [5; 1; 3].[Animace] Aplikace kótovaného promítání: Řešení střechy:  [Střecha 1 (Animace).] [Střecha 2 (Animace).] Opakování: Úlohy na procvičení.

• Mongeovo promítání. Zobrazení bodu, přímky a roviny.
  
  

  PŘEDNÁŠKA 6-7 Úvod do Mongeova promítání - zobrazení bodu, přímky a roviny. Úkol 1: Sestrojte stopy roviny dané (i) třemi body, (ii) dvěma rovnoběžkami. [Zadání v pdf] Úkol 2: Sestrojte sdružené průměty hlavních přímek h, f roviny σ, která je dána dvěma rovnoběžkami a, b. Zobrazte stopy roviny σ. [Animace] Řešené příklady z přednášky: Příklad 8: Sestrojte stopy roviny σ dané různoběžkami a, b.  [Animace (stopníky)] [Animace (hlavní přmky)] Příklad 9: Sestrojte stopy roviny σ dané bodem A a přímkou b.   [Animace] Příklad 10: Určete sdružené průměty přímky AB, která leží v rovině ρ(-5; 5; 4); A = [0; 2; ?], B = [2; 1; ?]. [Animace, 3D znázornění: Přímka v rovině (GeoGebra 3D)] Příklad 12: Určete průsečík přímky AB s rovinou ν(-4; 4; 5), A = [2; 1; 0], B = [-5; 4; 8].   [Animace] Příklad 13: Bodem K = [2; 3; 4] veďte přímku kolmou k rovině ρ(-3; 4; 4). Příklad 14: Určete odchylku roviny ρ(-3; 4; 4) od půdorysny π.   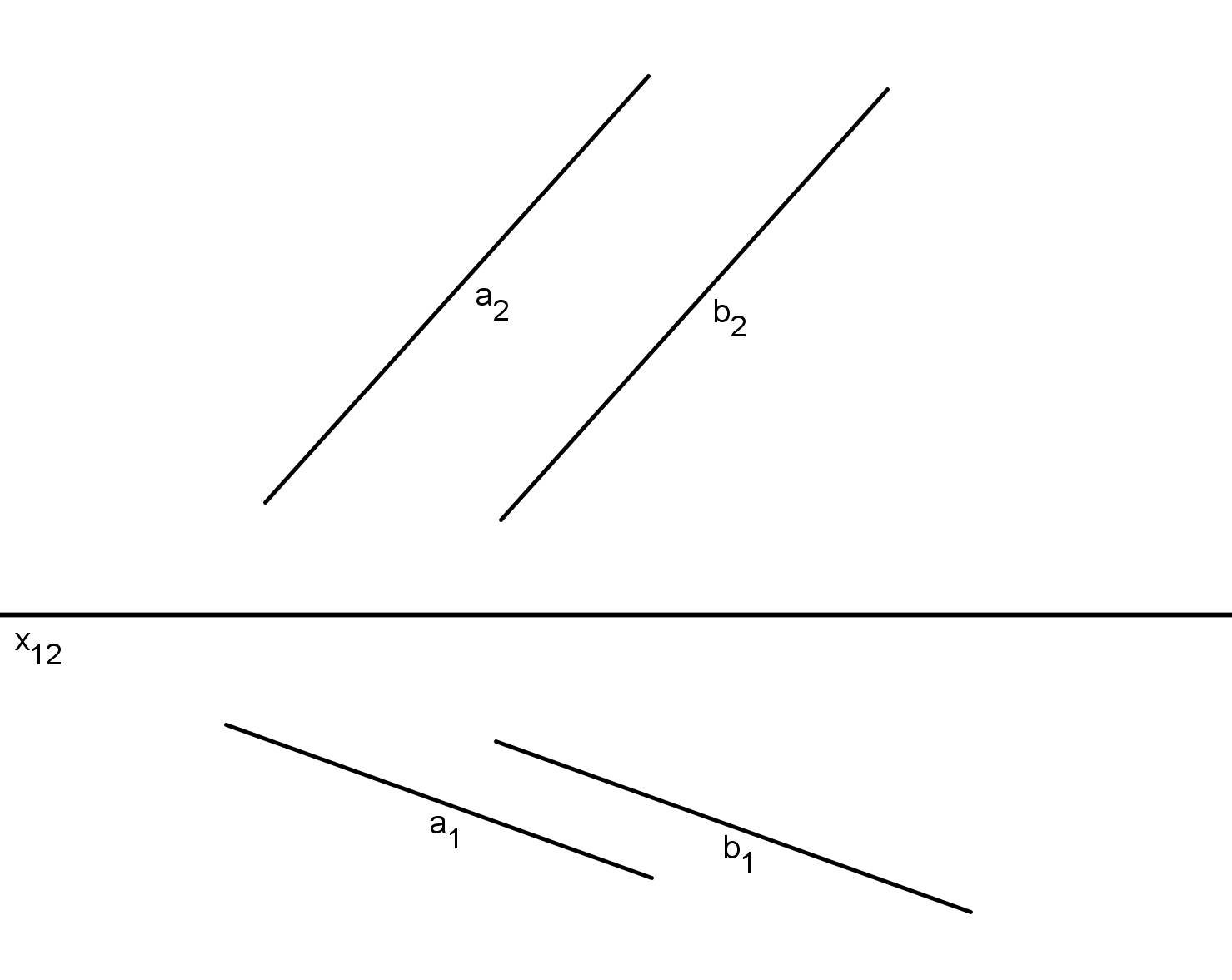[Animace] Samostatná práce:  Sestrojte stopy roviny dané přímkami a, b: Rovina je určena dvěma rovnoběžkami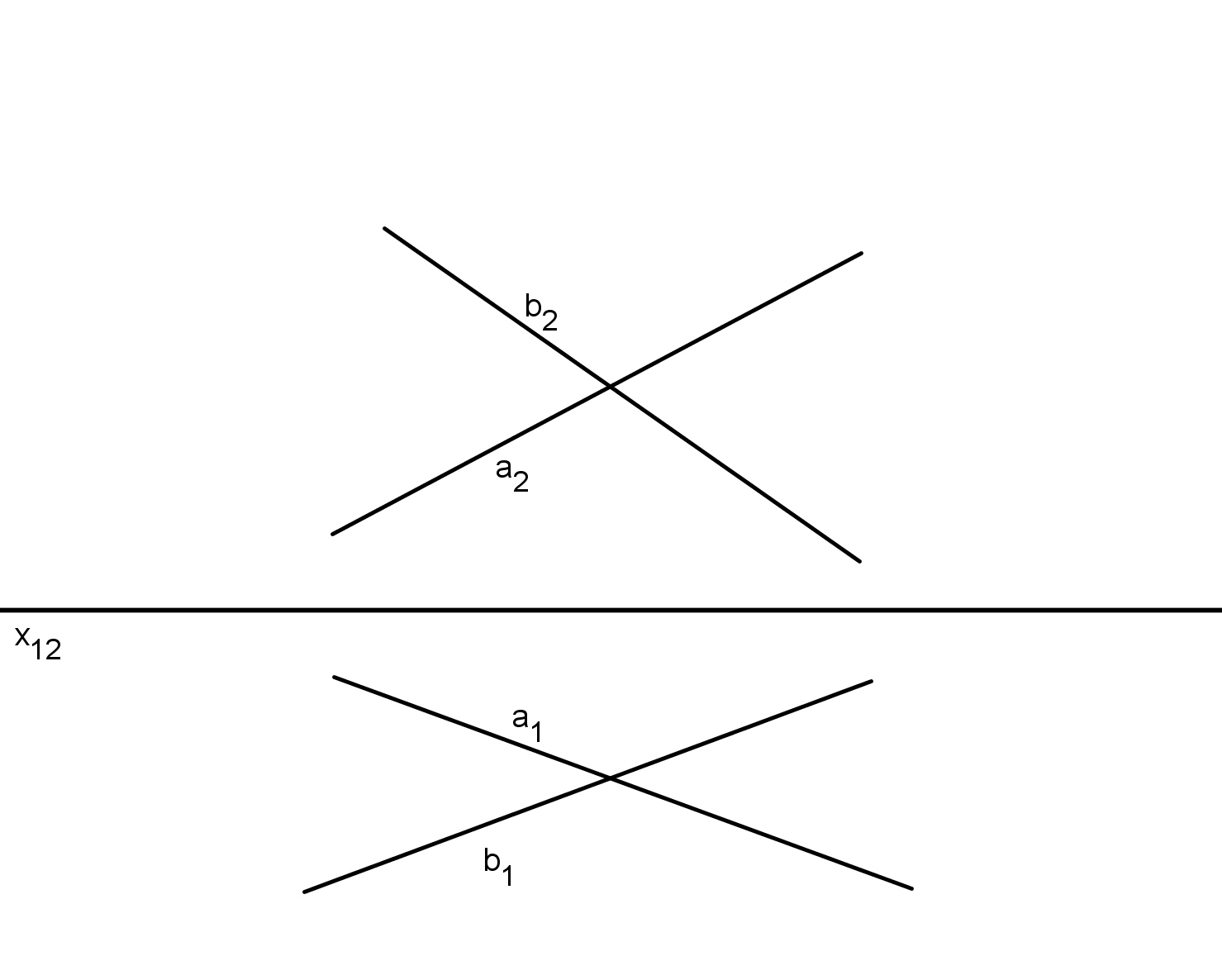 Rovina je určena dvěma různoběžkami

• Mongeovo promítání. Polohové úlohy.
• Mongeovo promítání. Polohové a metrické úlohy.
• Mongeovo promítání. Metrické úlohy. Zobrazení kružnice.
  
  

  PŘEDNÁŠKA 8-9 Mongeovo promítání II (metrické úlohy, kružnice). Příklad 15: Určete skutečnou velikost úsečky AB; A = [3; -1; 2], B = [0; 3; 3,5].   [Animace] Úkol 2: Určete vzdálenost bodu V=[5; 7; 7] od roviny ρ = (5; 4; 6). [Animace - sklopením]   [Animace - otočením] Úkol 3: Sestrojte v Mongeově promítání sdružené průměty kružnice k, která leží v rovině kolmé na nákresnu. [Animace] Úkol 4: Sestrojte v Mongeově promítání sdružené průměty kružnice k, která leží v obecně umístěné rovině. [Animace]

• Mnohostěny
  
  

  PŘEDNÁŠKA 10 Mnohostěny. Krychle – kvádr – hranol  /  Hranolová plocha – hranol  /  Objem jehlanu (You Tube) Úloha 1: Dokažte, že úsečky spojující středy protějších hran čtyřstěnu mají společný střed (tímto bodem je těžiště čtyřstěnu). [Konstrukce v GG (2D)] Úloha 2: Spojnice vrcholu čtyřstěnu s těžištěm protější stěny se nazývá těžnice čtyřstěnu.Těžnice čtyřstěnu mají společný bod – těžiště čtyřstěnu T. Vzdálenost těžiště čtyřstěnu od vrcholu je rovna 3/4 délky těžnice (viz Commandino's Theorem; Frederico Commandino). [Konstrukce v GG (2D)] Eulerova formule: On-line ověření  /  Wikipedia: Euler characteristic  /  dynamický (topologický) důkaz Platónská tělesa: Wikipedia: Platonic solid.

• Mnohostěny. Pravidelné mnohostěny. Zobrazení.
  
  

  PŘEDNÁŠKA 11-12 Pravidelné mnohostěny.

• Shrnutí.

Literatura

[1]  Drábek, K., Harant, F., Setzer, O.:. Deskriptivní geometrie I, SNTL, Praha 1978.
[2]  Kargerová, M., Deskriptivní geometrie- pro technické školy vysoké, vyšší a střední. Montanex, Praha, 2007.
[3]  Pomykalová, E., Deskriptivní geometrie pro střední školy. Prometheus, Praha, 2010.
[4]  Urban, A.:. Deskriptivní geometrie I, SNTL, Praha 1982.
[5]  Doležal, J.:. Základy geometrie a Geometrie, VŠB-TU Ostrava, on-line učebnice
      [http://mdg.vsb.cz/jdolezal/StudOpory/Uvod.html].
[6]  Pomykalová, E., Matematika pro gymnázia - Stereometrie. Prometheus, Praha, 1995.
[7]  Voráčová a kol., Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha, 2012.
[8]  Vrba, A.: Cabri 3D v2 Příručka pro uživatele.
      Online: http://www.pf.jcu.cz/cabri/cabri3d/download/Cabri_3D_prirucka.pdf

Internetové odkazy

Software ke stažení

sketchup.google.com ... aplikace Google SketchUp (možnost bezplatného stažení)
www.geogebra.org ... program GeoGebra (možnost bezplatného stažení)
www.rhino3d.com ... 3D modelovací program Rhinoceros
Dalest Elica ... podpora výuky stereometrie
dg.vidivici.cz ... Program Deskriptivní geometrie

Materiály pro výuku a sebevzdělávání

i2geo.net ... portál pro sdílení výukových materiálů dynamické geometrie
wiki.geogebra.org ... GeoGebra Wiki - manuál, výukové materiály, fórum apod.
wiki.geogebra.org/cs/ ... postupně překládaná česká verze GeoGebra Wiki
www.youtube.com/user/GeoGebraChannel ... GeoGebra na YouTube
www.geogebratube.org ... Materiály v GeoGebře ke stáhnutí
http://www.korthalsaltes.com ... Paper models of polyhedra

Požadavky na studenta

• Seminární práce.
  • Rysy.
    V průběhu semestru bude zadáno několik domácích úkolů k narýsování (vybrané z nich je možno po dohodě s vyučujícím rýsovat pomocí vhodného software).
    Zadání domácích úkolů.
  • 3D model.
    Vytvoření 3D modelu nějakého objektu (opět po dohodě s vyučujícím) v programu Google SketchUp nebo v jiném 3D modelovacím programu.
  • Tělesa.
    Vytvoření daného počtu papírových modelů vybraných mnohostěnů.
• Zkouška.
  • Písemná (narýsování zadané konstrukce) a ústní zkouška v rozsahu probíraného učiva.
    Otázky k ústní části zkoušky., Vzorové příklady k písemné části zkoušky.