GEOMETRIE I (KMA/7G1) - Cvičení

Předmět je zaměřen na afinní geometrii v prostorech dimenze 2 a 3 a na základní metody popisu těchto prostorů, vše v souvislostech s výukou matematiky.

Literatura ke studiu:

[1]  Pech, P., Analytická geometrie lineárních útvarů, České Budějovice, PF JU, 2004.

[2]  Hašek, R. Lineární algebra a geometrie, 21. 6. 2020.

[3]  Hašek, R. Lineární algebra, 29. 4. 2020. / Geometrický význam determinantu. [Obsah rovnoběžníku] [Objem rovnoběžnostěnu]

Osnova

• Afinní bodový prostor. Parametrické vyjádření afinního bodového podprostoru; přímky, roviny.

Cvičení č. 1


[2] Příklady: str. 126–129 (afinní bodový prostor), 136–140 (parametrické vyjádření afinního bodového podprostoru) Cvičení: str. 130 (afinní bodový prostor), 141 (parametrické vyjádření afinního bodového podprostoru) [1] Cvičení: str. 25 Prémiový úkol č. 1: V rovině je dán trojúhelník ΔABC. Určete všechny body X takové, že úsečky XA, XB a XC mohou být v rovině posunuty, bez otočení či změny délky, tak, že vytvoří trojúhelník. [GeoGebra: Ilustrace řešení]

• Obecná rovnice nadroviny. Rovnice přímky v rovině a roviny v prostoru.

Cvičení č. 2


Prémiový úkol č. 2: Navrhněte početní metodu určení, zda daný bod náleží danému trojúhelníku. Metodu demonstrujte na příkladu trojůhelníku ΔABC; A = [-13, -5], B = [5, 2], C = [-6, 10], a bodů K = [-3, 8], M = [-8, -3], P = [-6, 4] a Q = [2, 4].

• Vzájemné polohy afinních bodových podprostorů; bodů, přímek a rovin.

Cvičení č. 3


Parametrické rovnice přímky a roviny, obecná rovnice roviny, vzdálenosti a odchylky. Prémiový úkol č. 3: Kolik trojúhelníků můžeme vepsat pravidelnému n-úhelníku tak, aby jejich vrcholy ležely ve vrcholech n-úhelníku ale jejich strany nebyly totožné s jeho stranami? Například pro pravidelný sedmiúhelník existuje sedm takových trojúhelníků.

Cvičení č. 4


[1] Cvičení: str. 57-58/cv. 5-10 [2] Příklady a cvičení: str. 160–167 (vzájemná poloha afinních bodových podprostorů) Prémiový úkol č. 4: Je možné libovolnému čtyřstěnu opsat kulovou plochu? Pokud ano, jak najdeme její střed?

• Skalární součin. Odchylka vektorů. Eukleidovský bodový prostor.

Cvičení č. 5


[1] str. 85-88 [2] Příklady a cvičení: str. 58–77 (skalární součin) Prémiový úkol č. 5: Body A = [5, 4, 6], B = [1, 0, 4] jsou sousedními vrcholy krychle ABCDEFGH v trojrozměrném prostoru, jejíž vrchol C leží v rovině xy. Vypočítejte souřadnice zbývajících vrcholů krychle.

• Vektorový a smíšený součin.

Cvičení č. 6


Opakování tématu "vzájemné polohy afinních bodových podprostorů", řešení úloh ze str. 365-367 sbírky Bušek, I. Řešené maturitní úlohy z matematiky. Praha: SPN, 1985.

• Vzdálenosti a odchylky bodových podprostorů; bodů, přímek a rovin.

Cvičení č. 7


Test č. 1

• Objem simplexu. Obsah trojúhelníku, objem čtyřstěnu.

Cvičení č. 8


Obsah rovnoběžníku a trojúhelníku. Objem rovnoběžnostěnu a simplexu. Obecná rovnice roviny užitím vnějšího součinu.

• Afinní zobrazení. Afinní transformace roviny a prostoru. Samodružné body a směry.

Cvičení č. 9


Objem rovnoběžnostěnu ÚKOL č. 1:  Vypočítejte objem čtyřstěnu, jehož stěny leží ve čtyřech rovinách daných rovnicemi x + y + z - 10 = 0, 2x + 6y - z + 2 = 0, -x - y + 9z - 7 = 0, x - y - z + 9 = 0. [Řešení v GeoGebře] ÚKOL č. 2:  Čtyřstěn je dán body A[1, -5, 4], B[0, 3, 1], C[-2, -4, 3], D[4, 4, -2]. Vypočtěte jeho objem V a jeho výšku vA spuštěnou z bodu A na podstavu BCD. [Řešení v GeoGebře] Prémiový úkol č. 6: Jaký největší balík ve tvaru kvádru můžete zavázat níže zobrazeným způsobem, pokud máte k dispozici provaz o dělce 12 stop? Spotřebu části délky provazu na vázání uzlů neuvažujeme.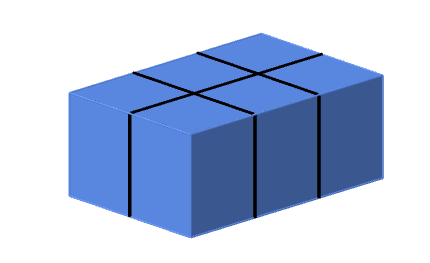

• Základní afinity. Osová afinita. Modul afinity.

Cvičení č. 10


[1] Příklady a cvičení: str. 132, 136, 143, 159-160 [2] Příklady: str. 169–177 Prémiový úkol č. 7: Z určitého počtu jednotkových krychlí je sestavena větší krychle. U té jsou potom nabarveny některé stěny, ne však všechny. Po zaschnutí barvy je velká krychle rozložena zpět na jednotkové krychle. Jejich detailním průzkumem bylo zjištěno, že 218 z nich má na sobě barvu. Jaké byly rozměry velké krychle?

• Shodnosti v rovině a v prostoru. Grupa shodností.
• Podobnosti v rovině a v prostoru. Grupa podobností.
• Stejnolehlost.

Literatura

[1]  Pech, P., Analytická geometrie lineárních útvarů, České Budějovice, PF JU, 2004.
[2]  Hašek, R. Lineární algebra a geometrie, 21. 6. 2020.
[3]  Krieg, J., Vaňatová, L., Analytická geometrie lineárních útvarů, České Budějovice, PF JU, 1994.
[4]  Sekanina, M. a kol., Geometrie I, SPN, 1986.
[5]  Bican, L., Lineární algebra, Praha, SNTL 1979.
[6]  Motl, L., Zahradník, M., Pěstujeme lineární algebru, 3. vyd. Praha : Univerzita Karlova v Praze, nakladatelství Karolinum, 2002 [online verze].

Internetové odkazy

Software ke stažení

www.geogebra.org ... bezplatně dostupný program GeoGebra
wxmaxima.sourceforge.net ... bezplatně dostupný CAS program wxMaxima

Materiály pro výuku a sebevzdělávání

www.khanacademy.org/math ... Khan academy
www.geogebratube.org ... Materiály v GeoGebře ke stáhnutí