GEOMETRIE II (KMA/7G2)

Předmět je zaměřen na kuželosečky a kvadratické plochy.

Osnova

• Kuželosečky.

  Wikipedia: Conic section - Ellipse - Hyperbola - Parabola

  Řezy kuželové plochy rovinou (3D) - Řezy kuželové plochy rovinou (2D)

  

  ÚKOL:  Odvoďte rovnice daných křivek jako množin bodů dané vlastnosti: kružnice - elipsa - hyperbola - parabola.

  Řešení: viz [1] (Kuželosečky): elipsa (str. 8-10), hyperbola (str. 28-29), parabola (str. 45-46).

  
  

  DOMÁCÍ ÚKOL:  Řešte úlohy zadané 22. 2. prostřednictvím týmu Geometrie 2 - KMA/7G2 (2021/22) v MS Teams.

  
  

  Řídící přímka kuželosečky

  Každou regulární kuželosečku s výjimkou kružnice lze vytvořit jako množinu bodů v rovině, které mají od daného bodu F této roviny a od dané přímky d této roviny, přičemž F neleží na d, stálý poměr vzdáleností rovný kladnému číslu ε. Přímka d je řídící přímka kuželosečky, F je její ohnisko. Číslo ε je číselná výstřednost (numerická excentricita) kuželosečky. Pro ε rovno 1 je vzniklá kuželosečka parabola, pro ε větší než 1 hyperbola a pro ε menší než 1 elipsa.

      GeoGebra applet: [Kuželosečka daná řídící přímkou a ohniskem]

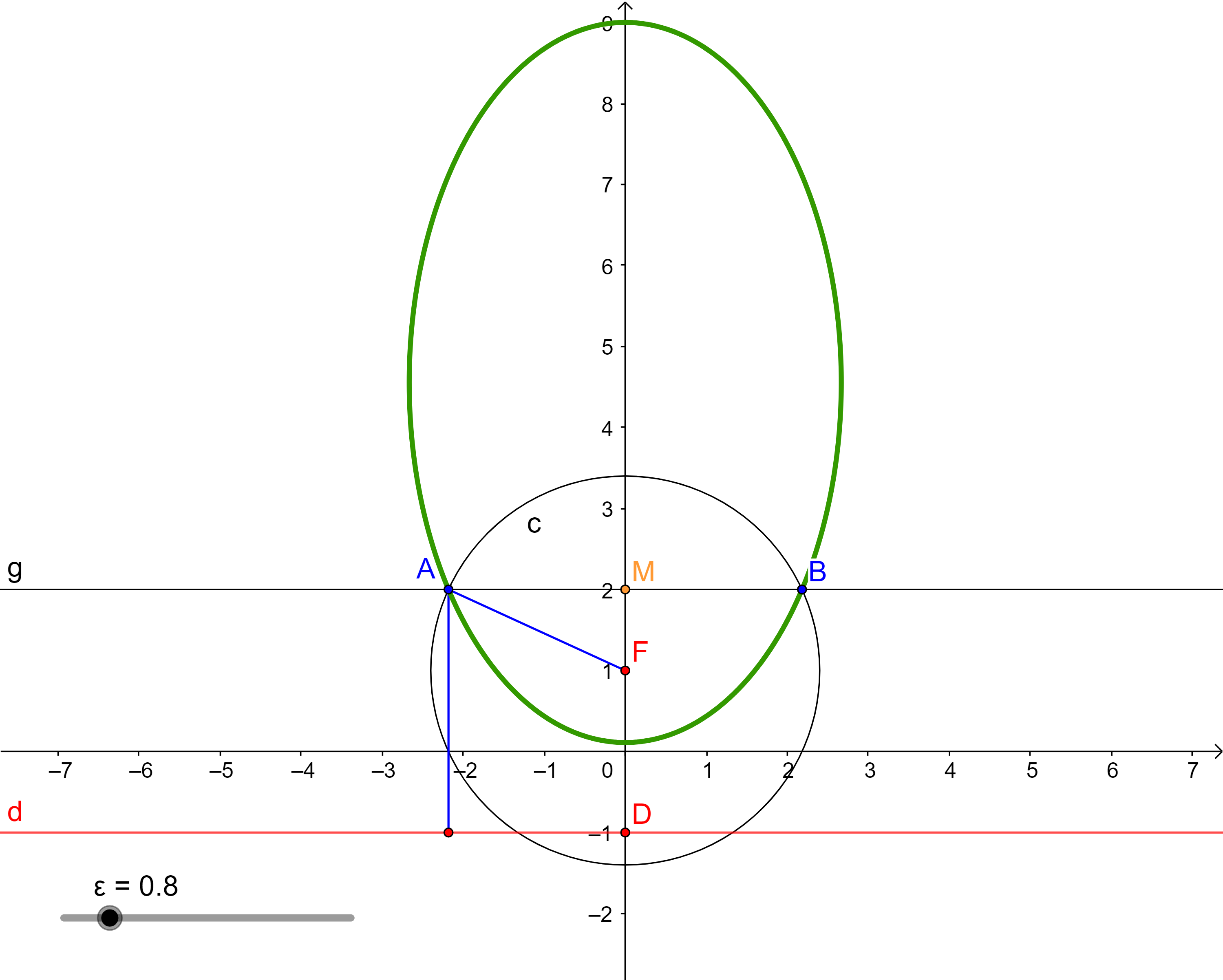
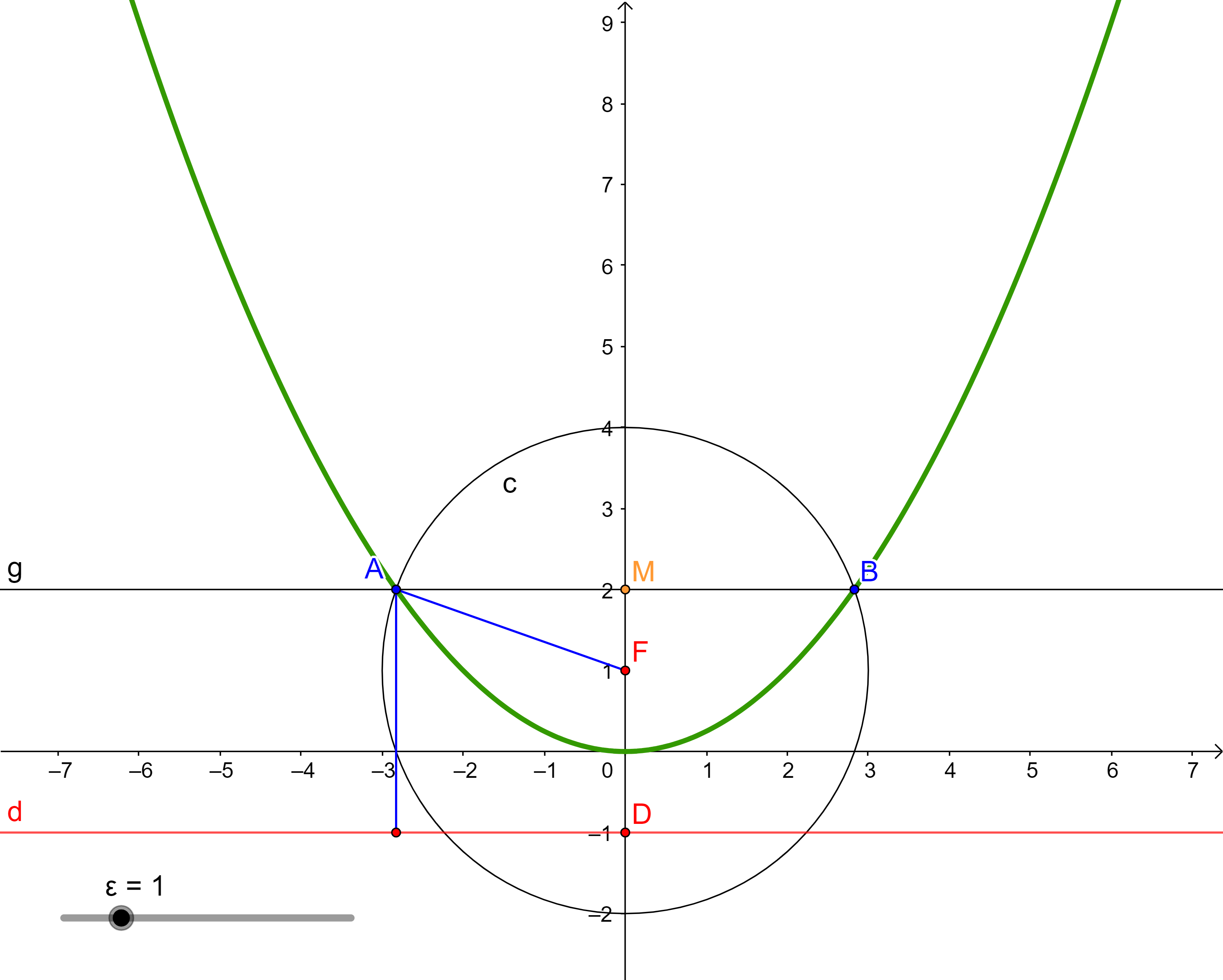
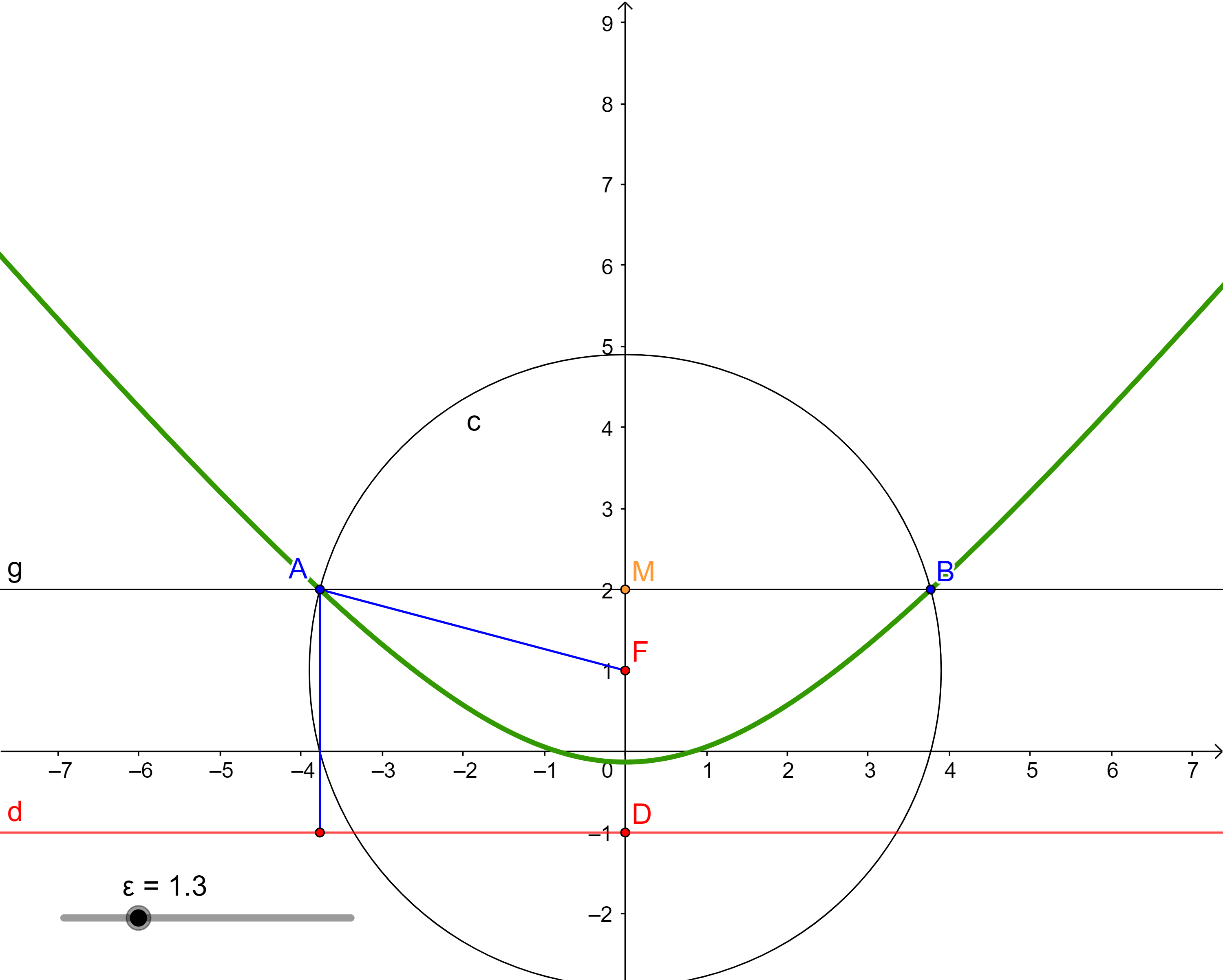
• Konstrukce kuželoseček.
  
  

  Zahradnická konstrukce elipsy

  [1] (Kuželosečky) (str. 12)

  Trojúhelníková a proužková konstrukce kuželosečky

  [1] (Kuželosečky) (str. 13-15)

  Bodová konstrukce kuželosečky

  [1] (Kuželosečky): elipsa (str. 10), hyperbola (str. 31), parabola (str. 46) / GeoGebra applety: [elipsa] [hyperbola] [parabola]

  Oskulační kružnice kuželosečky

  Oskulační kružnicí rozumíme kružnici, která se dotýká uvažované křivky v bodě, v němž s ní má společnou tečnu a ze všech takových kružnic se ke křivce nejvíce přimyká.

  

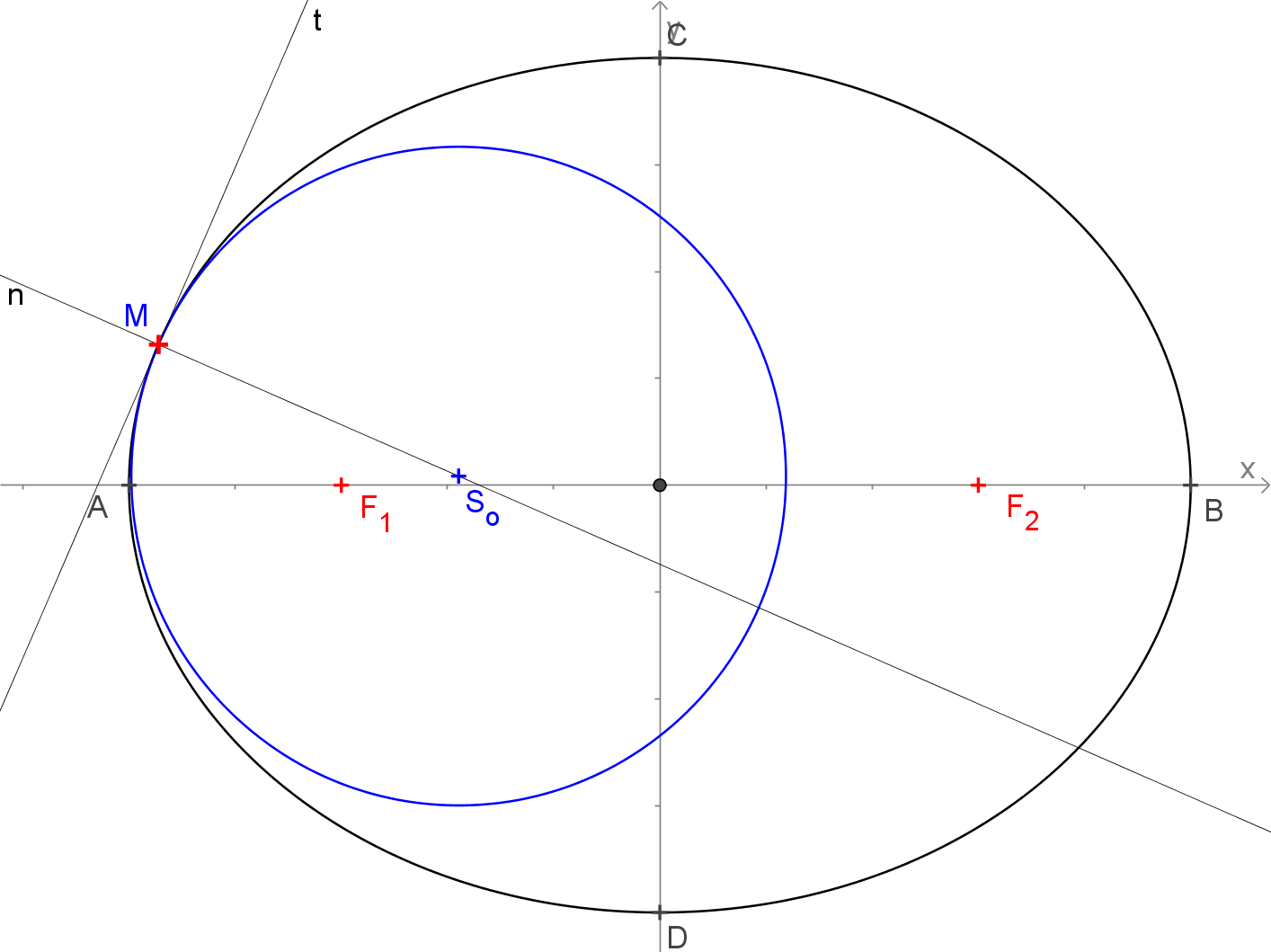
  Poloměr R oskulační kružnice v konkrétním bodě křivky nazýváme poloměrem křivosti v tomto bodě. Převrácenou hodnotou tohoto poloměru je potom křivost křivky v daném bodě, značíme ji k.

  Oskulační kružnice ve vrcholech elipsy jsou výjmečné tím, že mají s elipsou společný právě jeden bod, onen vrchol. Proto se jim často říká hyperoskulační kružnice, případně superoskulační kružnice.

  Konstrukce středů oskulačních kružnic regulárních kuželoseček
      GeoGebra applety: [elipsa] [hyperbola] [parabola]

  Tečna kuželosečky (kružnice, elipsy, hyperboly, paraboly)

  • Tečna kuželosečky daného směru

    Příklad: Napište rovnice tečen kružnice $x^{2}+y^{2}-16=0$ rovnoběžných s přímkou $y=3x$.

  • Tečna kuželosečky v bodě dotyku T[m, n]

    GeoGebra applet: [Tečna kuželosečky v daném bodě]

  • Tečna kuželosečky z bodu P[m, n]

    Příklad: Určete body dotyku tečen vedených bodem $O[0; 0]$ ke kružnici s rovnicí $x^{2}+y^{2}+10x+10y+49=0$.

  Domácí úkol:  [1] (Kuželosečky): Str. 25/Cvičení 6, 7, 8.

  Příklady k řešení (1-11)

  Polára p bodu P vzhledem ke kuželosečce

  Polárou bodu P vzhledem ke kuželosečce rozumíme přímku p. Bod P nazýváme pólem. Pro vnější body je to přímka spojující body dotyku tečen vedených z tohoto bodu ke kuželosečce.

  • GeoGebra applet: [Pól a polára vzhledem ke kuželosečce]

  Konstrukci poláry vzhledem k vnitřnímu bodu pak napomůže následující věta.

  Věta: Nechť p je polára bodu P a q je polára bodu Q. Pokud Q leží na p, potom q prochází bodem P.

  • Úkol: Sestrojte poláru m bodu M ležícího uvnitř kružnice k.
• Ohniskové vlastnosti kuželoseček.

  • Elipsa

    Věta: Tečna elipsy půlí vnější úhly průvodičů bodu dotyku.

     
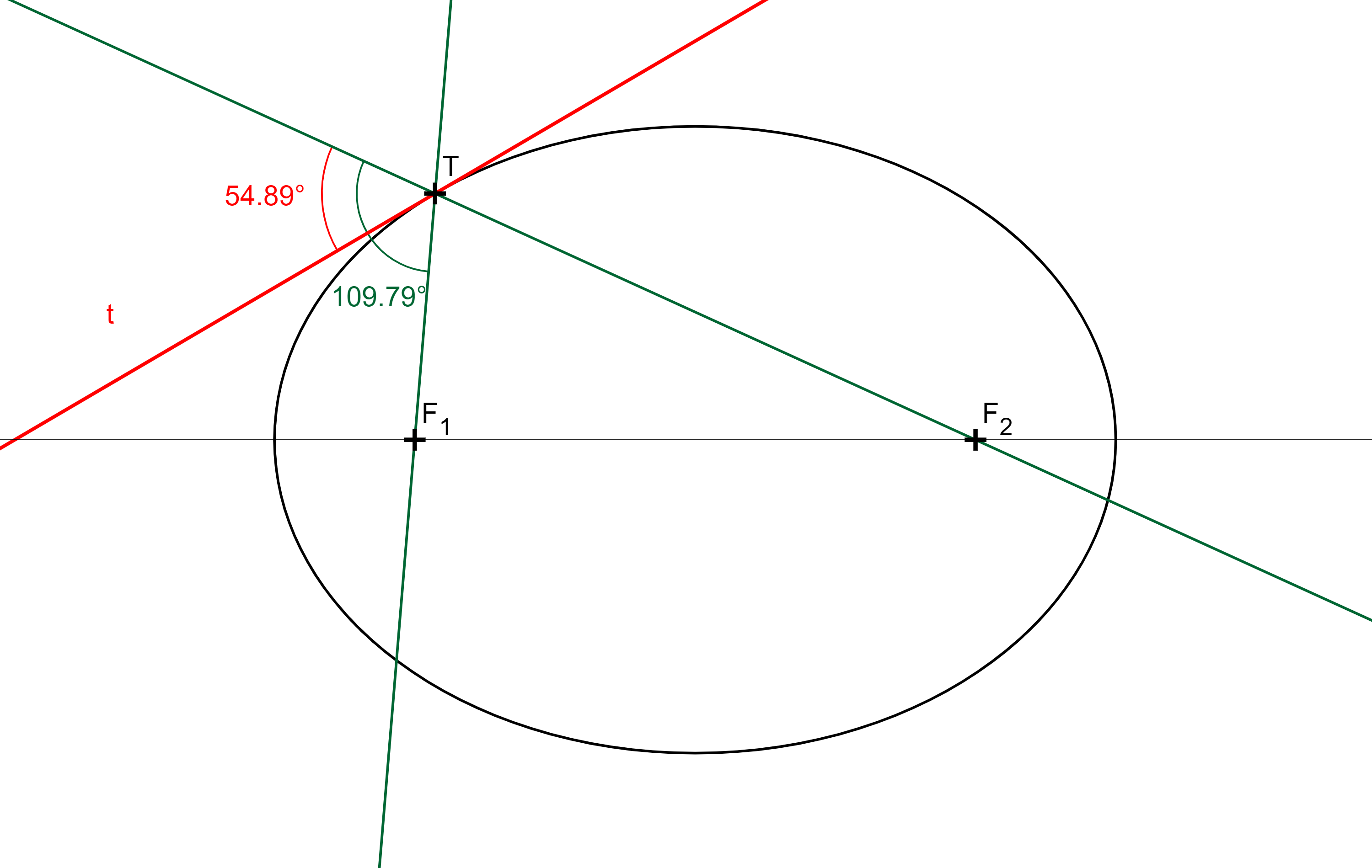
    GeoGebra

    Praktické využití uvedené vlastnosti viz např. Whispering gallery, Lithotripsy (litotripse), Feynman's lost lecture, Pech, P. Kuželosečky, Příklad na str. 23-24.

    Věta: (Řídící kružnice elipsy) Množina všech bodů souměrně sdružených s jedním ohniskem elipsy podle jejích tečen je kružnice se středem v druhém ohnisku a o poloměru rovném velikosti hlavní osy elipsy (tj. 2a).

    Poznámka: Řídící kružnice jsou dvě, se středy v obou ohniscích elipsy.

    Věta: (Vrcholová kružnice elipsy) Množina všech pat kolmic spuštěných z ohnisek elipsy na její tečny je kružnice opsaná kolem středu elipsy s poloměrem rovným délce hlavní polosy (tj. a).

  • Hyperbola

    Věta: Tečna hyperboly půlí vnější úhly průvodičů bodu dotyku.

     
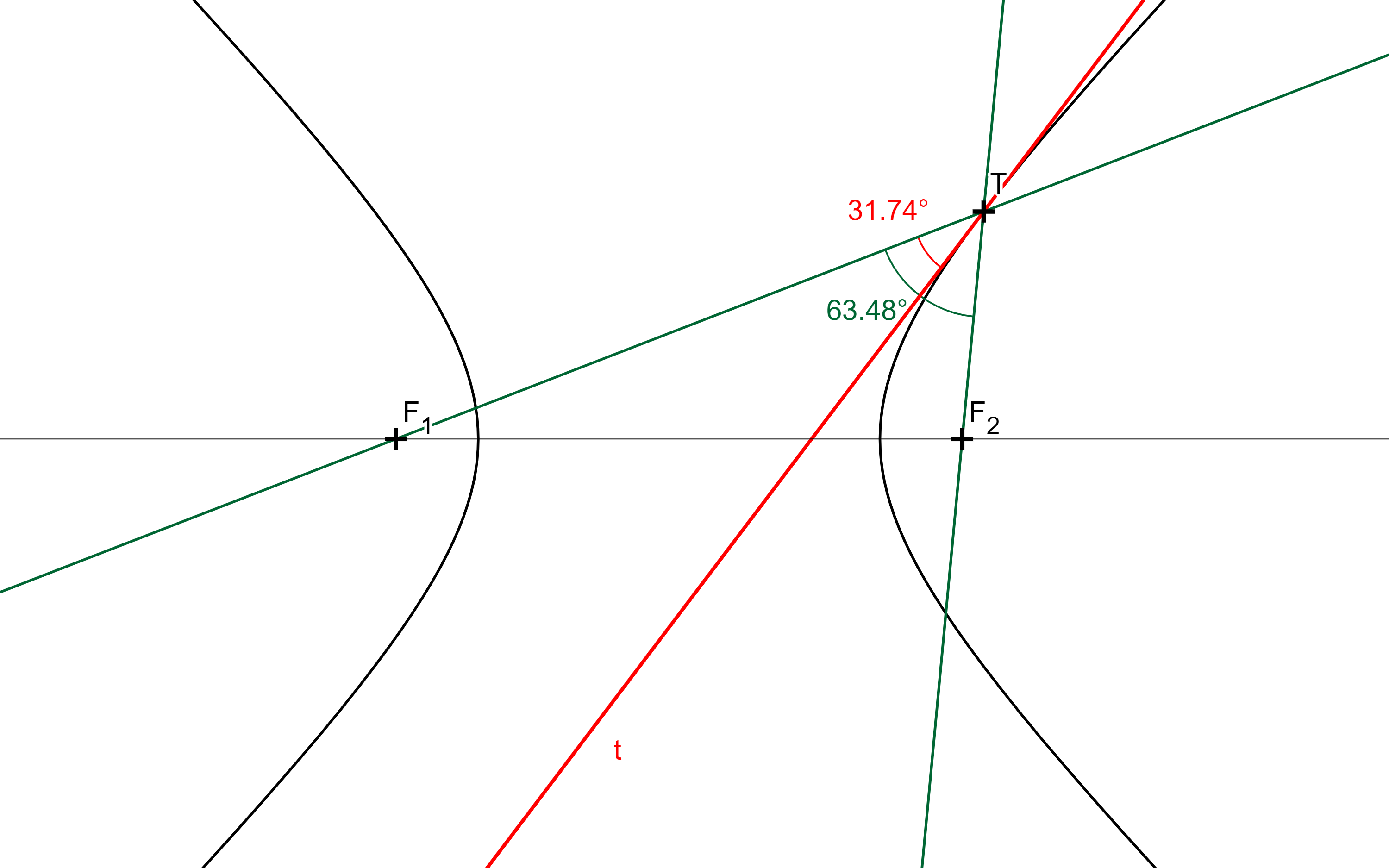
    GeoGebra

  • Parabola

    Věta: Tečna paraboly půlí vnější úhly průvodičů bodu dotyku (jedním z průvodičů je přímka určená bodem dotyku a ohniskem, druhým pak je kolmice spuštěná z bodu dotyku na řídící přímku).

    Praxe viz např. Novinky.cz: Za požár v domě mohlo kosmetické zrcátko.

  Příklady k řešení: 
  ÚKOL 1 (Ohniskové vlastnosti elipsy).pdf ; {Řešení: Příklad 1, Příklad 2, Příklad 3, Příklad 4}
  ÚKOL 2 (Ohniskové vlastnosti paraboly).pdf; {Řešení: Příklad 1, Příklad 2}
  

• Kanonický tvar rovnice kuželosečky pomocí otočení.

  wxMaxima: Algebraická rovnice kuželosečky / wxMaxima download

  GeoGebra: Uvedení rovnice na kanonický tvar

• Tečna, polára, sdružené průměry.

  Asymptotické směry: GeoGebra: Zobrazení kružnice ve středové kolineaci

  Rytzova konstrukce: GeoGebra: Postup Rytzovy konstrukce

• Vlastnosti kuželoseček. Aplikace.

  Quételetova-Dandelinova věta pro válcovou plochu: Řez rotační válcové plochy rovinou, která je kosá k ose plochy, je elipsa. Jejími ohnisky jsou dotykové body kulových ploch, které jsou válcové ploše vepsány a dotýkají se roviny řezu. Délka její vedlejší poloosy se rovná poloměru válcové plochy ([1], str. 187).

             
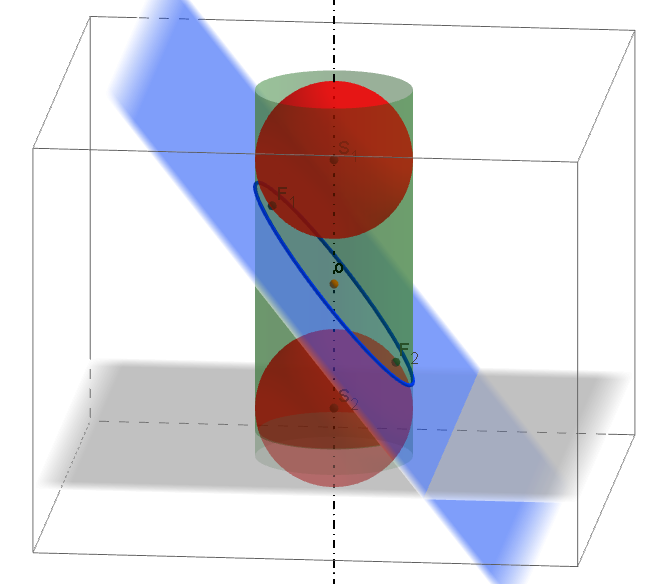
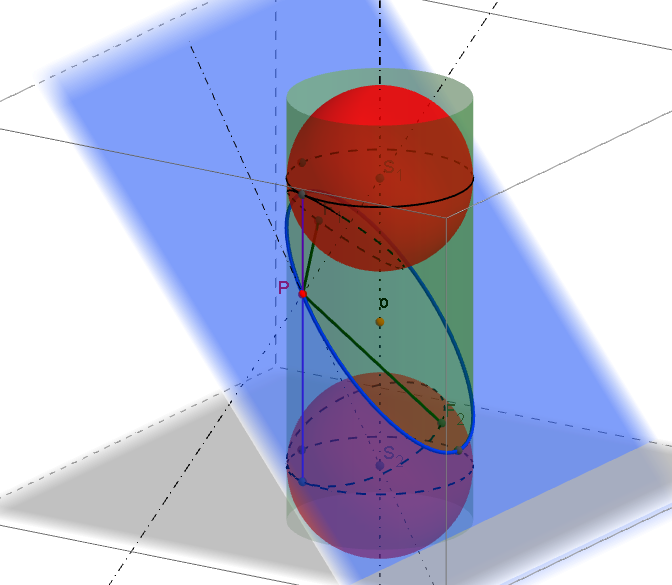
  Quételetova-Dandelinova věta pro válcovou plochu a její důkaz

  Quételetova-Dandelinova věta pro kuželovou plochu: Rovina, která naní vrcholová, ani není kolmá k ose a která s rovinou povrchové kružnice rotační kuželové plochy svírá úhel menší než povrchové přímky plochy, protíná rotační kuželovou plochu v elipse. Jejími ohnisky jsou dotykové body kulových ploch, které jsou vepsány kuželové ploše a dotýkají se roviny řezu ([1], str. 208).

             
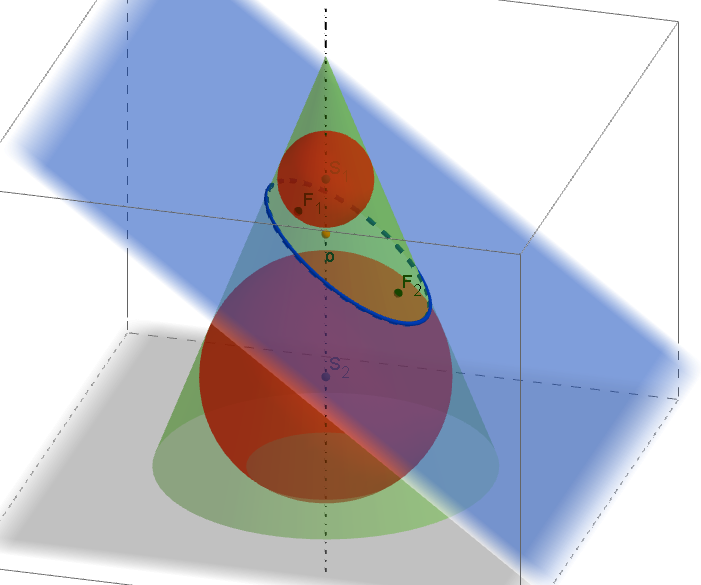
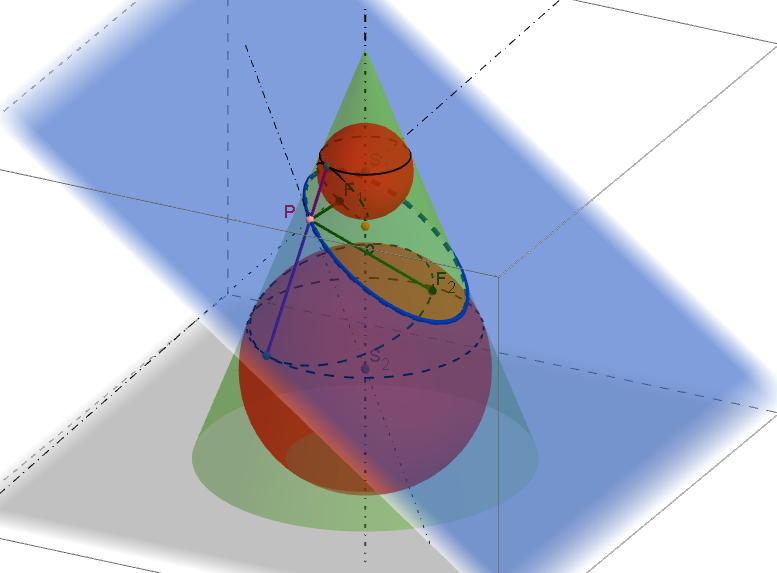
  Quételetova-Dandelinova věta pro kuželovou plochu a její důkaz

• Charakteristická rovnice.
• Kanonický tvar rovnice kuželosečky pomocí charakteristické rovnice.
• Kvadriky.
• Kanonický tvar rovnice kvadriky.
• Vlastnosti kvadrik.

Literatura

[1]  Pech, P. (2004) Kuželosečky.
[2]  Hašek, R., Pech, P. (2010) Kvadratické plochy a jejich reprezentace v programu Maple.
[3]  Boček, L., Kočandrle, M. (2009) Analytická geometrie (Matematika pro gymnázia). Prometheus, Praha.
[4]  Voráčová a kol. (2012) Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha.
[5]  Budinský, B. (1983) Analytická a diferenciální geometrie. SNTL, Praha.
[6]  Kuřina, F. (1996) 10 pohledů na geometrii. Praha: Akademie věd České republiky.
[7]  Polák, J. (2015) Přehled středoškolské matematiky. Praha: Prometheus. [8]  Sekanina, M. a kol. (1988) Geometrie II, SPN, Praha.

Internetové odkazy

Software ke stažení

www.geogebra.org ... bezplatně dostupný program GeoGebra
wxmaxima.sourceforge.net ... bezplatně dostupný CAS program wxMaxima

Materiály pro výuku a sebevzdělávání

www.khanacademy.org/math ... Khan academy

Zkouška

Zkouška bude mít dvě části, písemnou a ústní.
V písemné části budou řešeny dva příklady vybrané z: {[1]; str. 89/2; str. 112/11; str. 121/4, 5, 6, 8, 9, 10, 11, 12; str. 134/7; str. 141/1}.
Ústní část pak bude spočívat v zodpovězení jedné otázky vylosované z 7G2: otázky ke zkoušce.