Úvod do studia matematiky II - KMA/7UM2 |
Předmět Úvod do studia matematiky II je věnován úvodu do elementární geometrie a jejímu zařazení do kontextu matematiky a matematického učiva. Pojmy a jevy zde naznačené budou detailně rozebírány v navazujících specializovaných kurzech geometrie (KMA/7G1 - Geometrie I, KMA/7G2 - Geometrie II, KMA/7G3 - Geometrie III, Odborná matematika III (nav.)).
Studijní texty ve formátu PDF
Vhodné studijní texty (než zde bude uveden text věnovaný přímo tomuto předmětu):
[Hašek: Úvod do geometrie (2019).]
[Hašek: Planimetrie (2020).]
[Hašek: Lineární algebra a geometrie (2020).]
Osnova předmětu
-
Úvod do geometrie.
PŘEDNÁŠKA 1 Úvod do geometrie
-
Geometrie vzniká z praktických důvodů (slovo geometrie pochází z řečtiny, geo- znamená "Země", -metron pak "měření").
Geometrie zrodila v Mezopotámii (první prameny pocházejí z doby kolem 3000 př. n. l.) a v Egyptě jako umění vyměřování polí a základů staveb a určování
objemů různých schránek na obchodované zboží.
[Úvod do geometrie (2019), str. 4-8.] -
Základy geometrie jako vědy byly položeny řeckými matematiky (Thalés z Milétu, 624?-546? př. n. l.; Eukleidés, 300 př. n. l.; Archimédés, 287-212 př. n. l.).
[Úvod do geometrie (2019), str. 9-11.]
[Eukleides, Eukleidovy základy (Elementa), překlad F. Servít, 1907.]
[Archimedes' Book of Lemmas.] -
Eukleidovská geometrie. Eukleidés ve svých Základech položil základy axiomatické výstavby geometrie (i celé matematiky). Při této formalizaci geometrie ale stále vycházel
z nazírání reálného světa. Eukleidovská geometrie je založena na 5 Eukleidových postulátech, viz Úvod do geometrie (2019), str. 11.
Pátý z nich sehrál výraznou roli ve vývoji geometrie, konkrétně v 19. století při "objevení" tzv. neeukleidovských geometrií
(Hyperbolická geometrie,
Eliptická geometrie).
[Geometrie III (2020), str. 106.]Principy eukleidovské geometrie uplatňují:
- planimetrie,
- stereometrie,
- deskriptivní geometrie,
- diferenciální geometrie,
- kinematická geometrie.
Revizi axiomatické výstavby geometrie vedoucí k její vyšší formalizaci provedl David Hilbert.
[Úvod do geometrie (2019), str. 11.] -
Neeukleidovské geometrie. Hyperbolická geometrie,
Eliptická geometrie.
[Geometrie III (2020), str. 106.] -
Topologie.
Topologie je matematická disciplína, která se zabývá vlastnostmi útvarů, které nejsou ovlivněny jejich deformacemi. Konkrétně takovými deformacemi, při kterých nedochází k trhání či proděravění útvarů, tj. připouštíme natahování, smršťování či kroucení, nepřipouštíme vytváření otvorů či dělení na více částí.
Zdroj: https://londonist.com/london/transport/modern-tube-map-harry-beck-1931-1933
-
Eulerův vztah
[počet stěn] + [počet vrcholů] - [počet hran] = 2
s + v - h = 2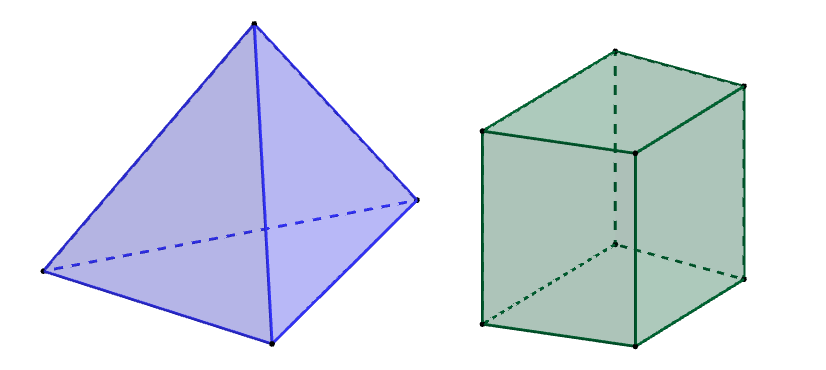
4 + 4 - 6 = 2 6 + 8 - 12 = 2Euler's Formula (www stránka) / Wikipedia: Euler characteristic / dynamický (topologický) důkaz
Prémiový úkol č. 1: Na obrázku jsou znázorněny hranice dvou pozemků. Jejich společná hranice je tvořena lomenou čarou. Nahraďte jí úsečkou tak, aby výměra zahrad zůstala zachována.
.png)
CVIČENÍ 1 Vytvořte si profil na stránce geogebra.org.
Důkazy geometrických vět. Vyslovte a dokažte následující věty:
-
Pythagorova věta.
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami.
Platí i věta obrácená: Pokud pro strany trojúhelníku s délkami a, b, c platí vztah a2 + b2 = c2, jedná se o trojúhelník pravoúhlý s přeponou c. Pythagorova věta má tedy podobu ekvivalence.
Eukleides (překl. F. Servít), Eukleidovy základy (Elementa) (1907). - Kniha 1. XLVII. (str. 24), Kniha 6. XXXI. (str. 101)
Úvod do geometrie (2019), str. 4-8.
Vizuální důkaz Pythagorovy věty z přednášky / Perigalův důkaz Pythagorovy věty / Henry Perigal (1801-1898)
James A. Garfield's Proof of the Pythagorean TheoremDůkaz Pythagorovy věty dle Eukleida [Kniha 1. XLVII. (Servít, 1907, str. 24)]: Pythagorova věta dle Eukleida 01 - dynamický důkaz, Pythagorova věta dle Eukleida - dynamický důkaz (02)
-
Eukleidovy věty.
Úvod do geometrie (2019), str. 12.
Eukleides (překl. F. Servít), Eukleidovy základy (Elementa) (1907). - Kniha 2. XIV. (str. 33), Kniha 6. VIII. (str. 88), XIII. (str. 91)
-
Thaletova věta.
Vrchol s pravým úhlem pravoúhlého trojúhelníku leží na kružnici, jejímž průměrem je přepona trojúhelníku, a naopak, jestliže vrchol trojúhelníku leží na kružnici, jejímž průměrem je jemu protilehlá strana, je u tohoto vrcholu pravý úhel.
Úvod do geometrie (2019), str. 10.
Eukleides (překl. F. Servít), Eukleidovy základy (Elementa) (1907). - Kniha 3. XXXI. (str. 51)
-
Věta o střední příčce trojúhelníku.
Střední příčkou trojúhelníku je úsečka spojující středy dvou stran trojúhelníku. Každá střední příčka trojúhelníku je rovnoběžná s protilehlou stranou (se kterou nemá společný bod) a její délka se rovná polovině délky této strany.
-
Dokažte, že střední příčky rozdělují trojúhelník na 4 shodné trojúhelníky, které jsou s ním podobné.
0,0ABCA1B1C1
-
Těžnice.
Těžnice trojúhelníku je úsečka, která spojuje vrchol trojúhelníku se středem protilehlé strany. Všechny tři těžnice trojúhelníku se protínají v jednom bodě, těžišti trojúhelníku, jehož vzdálenost od každého vrcholu je rovna dvěma třetinám délky příslušné těžnice.
-
Dokažte, že těžnice rozdělují trojúhelník na šest trojúhelníků, jejichž obsahy jsou shodné.
0,0ABCA1B1C1T
-
Dokažte pravdivost vztahu pro výpočet obsahu
- rovnoběžníku,
- trojúhelníku,
- lichoběžníku,
- kruhu. [YouTube: Area of a circle, formula explained]
ÚKOL č. 1: Dokažte Varignonovu větu.
Varignonova věta: Středy stran libovolného čtyřúhelníku tvoří rovnoběžník. (Pierre Varignon, 1654-1722)
ÚKOL č. 2: Vyberte si libovolné tvrzení z Eukleidových Základů (Eukleides, Eukleidovy základy (Elementa), překlad F. Servít, 1907.) nebo z Archimedovy Knihy lemmat (Archimedes' Book of Lemmas.) a zpracujte ho, jak nejlépe dokážete, ve formě materiálu na geogebra.org (můžete uvést i zadání, komentáře, obrázky, videa apod.).
-
Geometrie vzniká z praktických důvodů (slovo geometrie pochází z řečtiny, geo- znamená "Země", -metron pak "měření").
Geometrie zrodila v Mezopotámii (první prameny pocházejí z doby kolem 3000 př. n. l.) a v Egyptě jako umění vyměřování polí a základů staveb a určování
objemů různých schránek na obchodované zboží.
-
Geometrické útvary v rovině.
PŘEDNÁŠKA 2 Geometrické útvary v rovině
Úvod do geometrie (2019), str. 18-37.
-
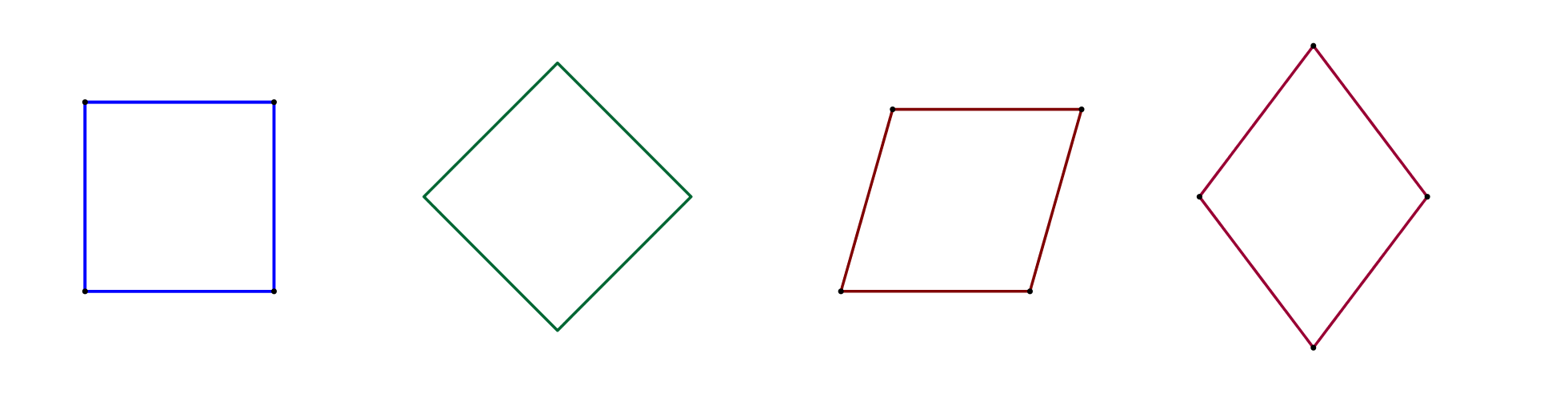
Jaké všechny útvary vidíte na obrázcích? Čím se liší levý a pravý útvar? Jakými pojmy to můžeme vyjádřit?


-
Dokážete pojmenovat zobrazené rovinné útvary?
-
O jakých vlastnostech trojúhelníku/čtyřúhelníku vypovídají uvedené obrázky?






-
Jakými pravidelnými mnohoúhelníky můžeme pokrýt rovinu (např. vydláždit podlahu)? Proč?


Klíčem k odpovědi na výše uvedenou otázku jsou velikosti vnitřních úhlů pravidelných mnohoúhelníků:




Euclidean tilings by convex regular polygons
Platonská tělesa (pravidelné mnohostěny)

-
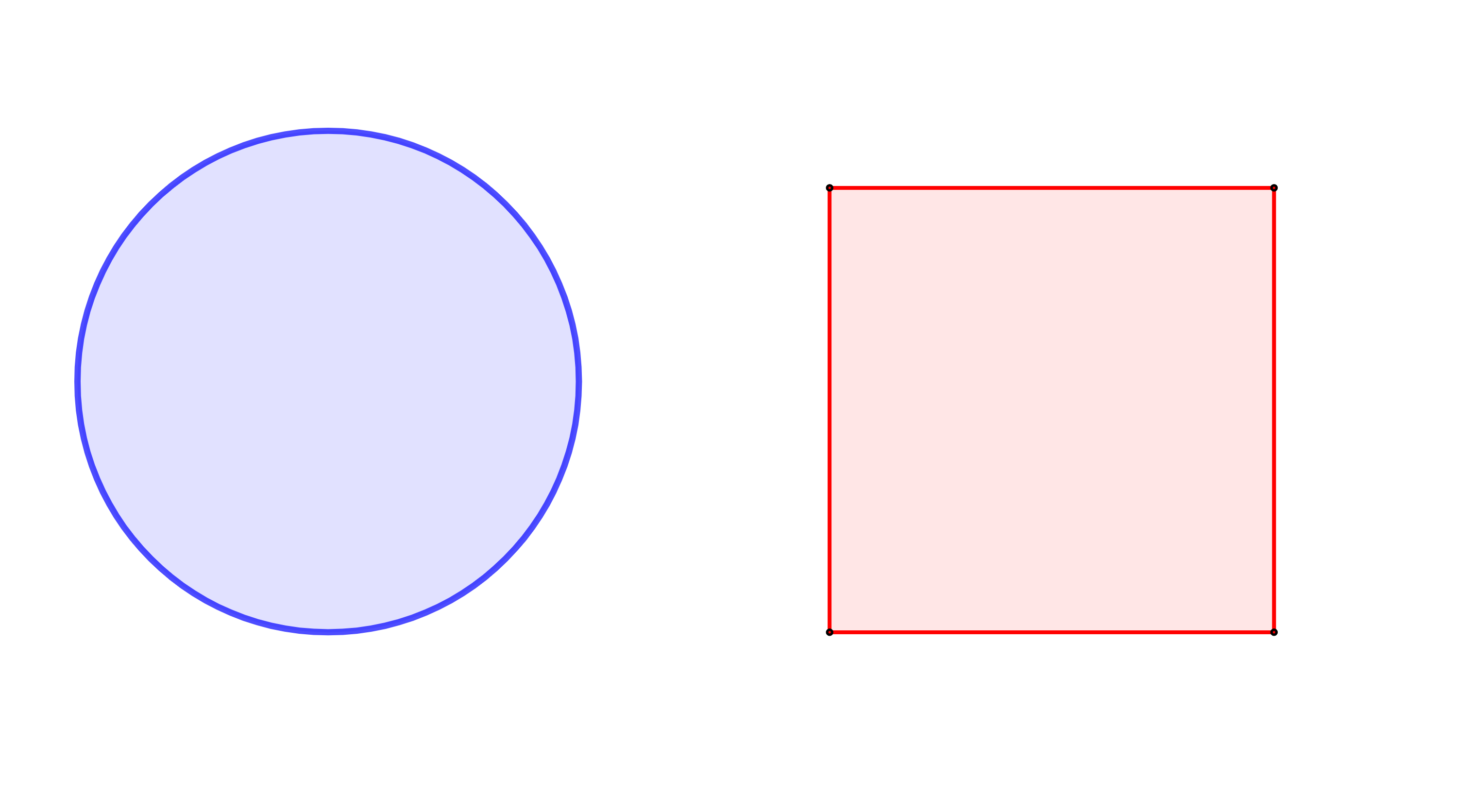
Jaký je rozdíl mezi kruhem a kružnicí?

Google Maps: Kansas
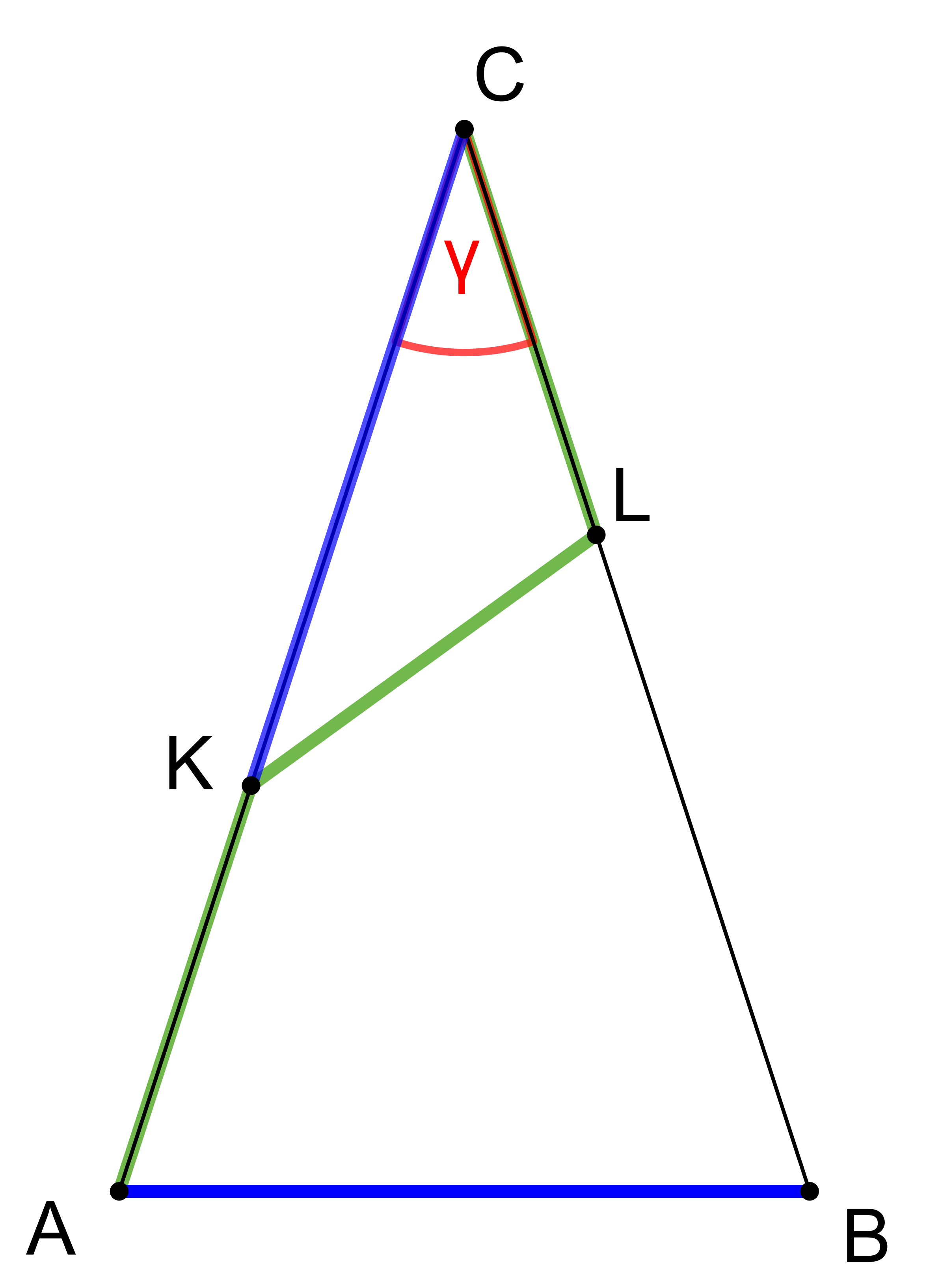
Prémiový úkol č. 2: V rovnoramenném trojúhelníku ABC leží na ramenech AC a BC po řadě body K a L tak, že |AK|=|KL|=|LC| a |KC|=|AB|, viz obrázek. Určete velikost úhlu ACB.
CVIČENÍ 2 Eukleidovské konstrukce, viz Úvod do geometrie (2019), str.~11.
- GeoGebra: [Applet pro eukleidovské konstrukce]
-
Mascheroniovy konstrukce
PŘÍKLAD: Je dána kružnice k(S;r); dále je dána dvěma body A, B (body neleží na kružnici) její sečna p, která neprochází středem S. Sestrojte průsečíky přímky p s kružnicí k, aniž přitom použijete pravítka.
GeoGebra: [Applet pro provedení konstrukce] [Řešení]
Lorenzo Mascheroni, 1750-1800, Georg Mohr, 1640-1697, Mascheroni Construction
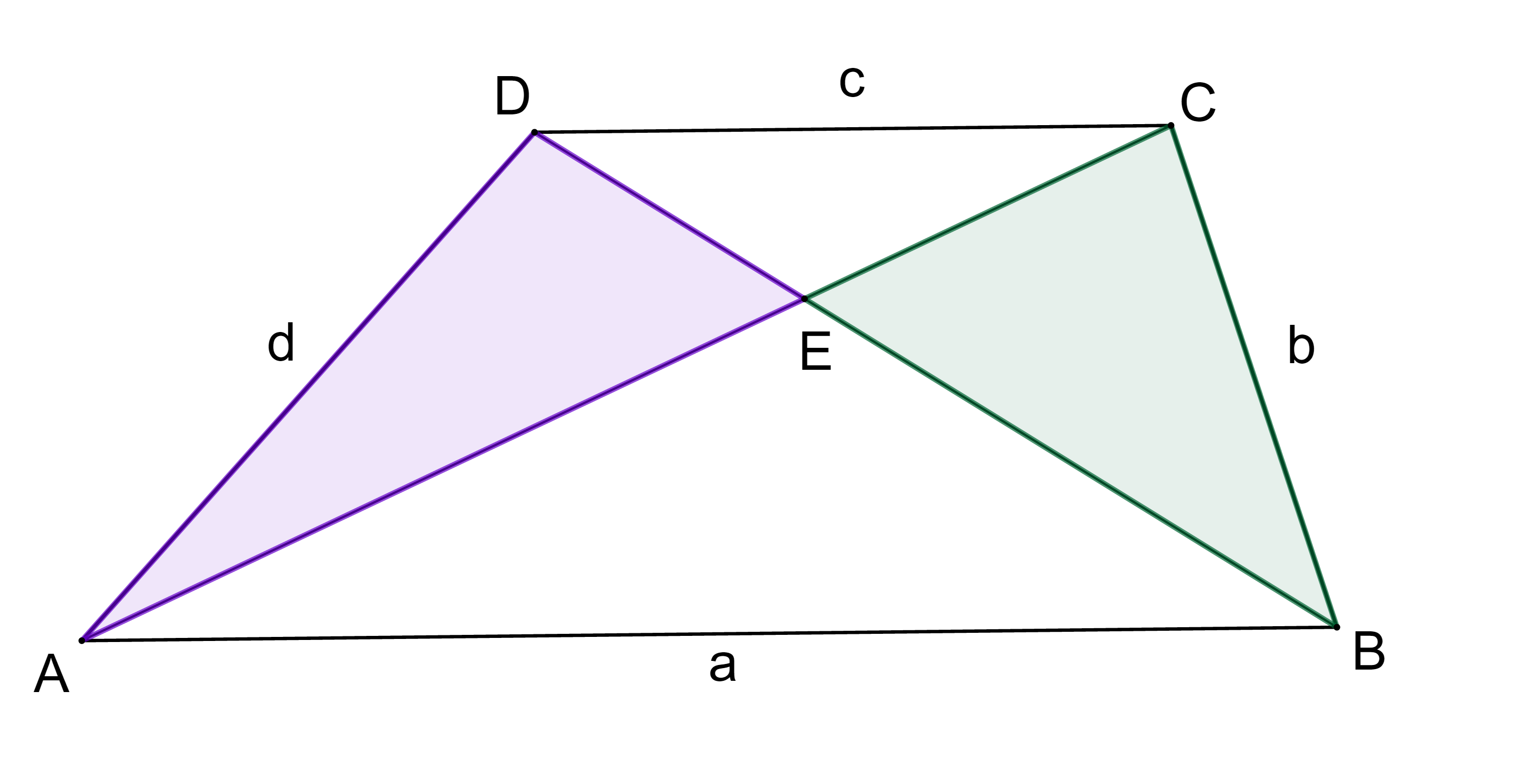
ÚKOL: Dokažte, že pro každý lichoběžník ABCD s průsečíkem úhlopříček E platí, že trojúhelníky DAE a BCE mají stejný obsah, viz obrázek. Jaký je potom vztah mezi trojúhelníky ABE a CDE?
ÚKOL: Charakterizujte následující rovinné útvary:
- bod, úsečka, lomená čára, mnohoúhelník,
- přímka, polopřímka, polorovina, úhel,
- mnohoúhelník
- trojúhelník; obecný, rovnoramenný, rovnostranný, ostroúhlý, pravoúhlý, tupoúhlý,
ÚKOL č. 2: Který z pravidelných mnohoúhelníků, kterými lze pokrýt rovinu (jedná se o rovnostranný trojúhelník, čtverec a pravidelný šestiúhelník), má při obsahu 1 m2 nejmenší obvod? Nejprve si tipněte, potom to spočítejte! Své řešení zpracujte tak, aby byl zřejmý postup Vašich výpočtů.
-
Jaké všechny útvary vidíte na obrázcích? Čím se liší levý a pravý útvar? Jakými pojmy to můžeme vyjádřit?
-
Geometrické útvary v trojrozměrném prostoru.
PŘEDNÁŠKA 3 Úvod do geometrie (2019), str. 18-37.
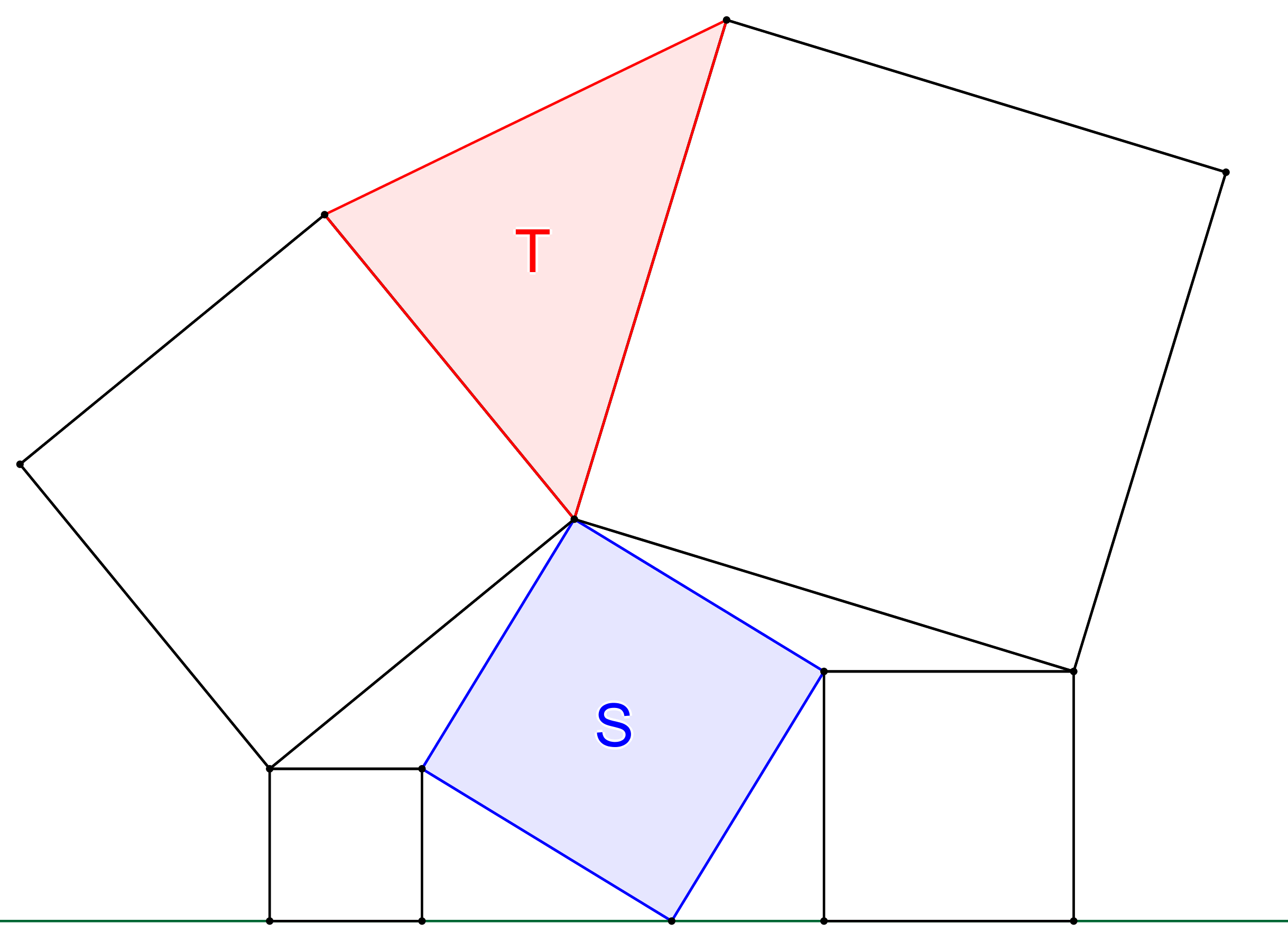
Prémiový úkol č. 3: Pět čtverců je uspořádáno jako na obrázku. Dokažte, že obsah (modrého) čtverce S je roven obsahu (červeného) trojúhelníku T.
CVIČENÍ 3 ÚKOL: Charakterizujte následující rovinné útvary:
-
mnohoúhelník
- čtyřúhelník; čtverec, obdélník, rovnoběžník, kosočtverec, kosodélník, tětivový čtyřúhelník, tečnový čtyřúhelník, deltoid, lichoběžník,
- konvexní, nekonvexní, pravidelný,
- kruh, kružnice. [YouTube: Area of a circle, how to get the formula.]
Příklady k řešení: Cvičení 3
ÚKOL č. 3: Sestrojte trojúhelník ABC jsou-li dány jeho těžnice ta, tb, tc.
-
mnohoúhelník
-
Míra. Délka úsečky. Dimenze prostoru. Měření úhlu.
PŘEDNÁŠKA 4 Úvod do geometrie (2019), str. 38-44.
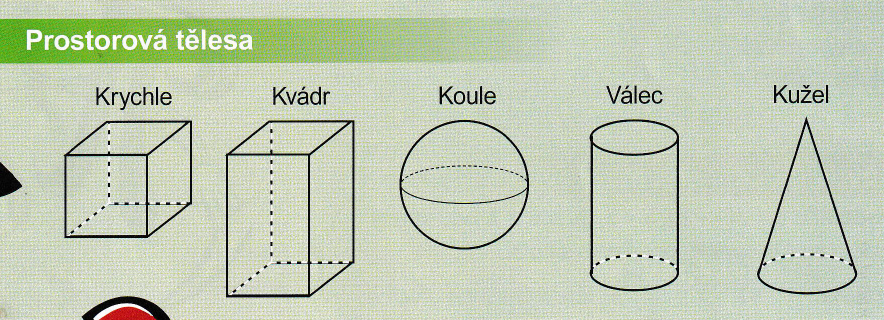
- hranol, jehlan, kvádr, krychle, rovnoběžnostěn
[Kosý šestiboký hranol (GeoGebra aplet)] [Kolmý pětiboký hranol (GeoGebra aplet)] [Pětiboký jehlan]
-
Pravidelné mnohostěny

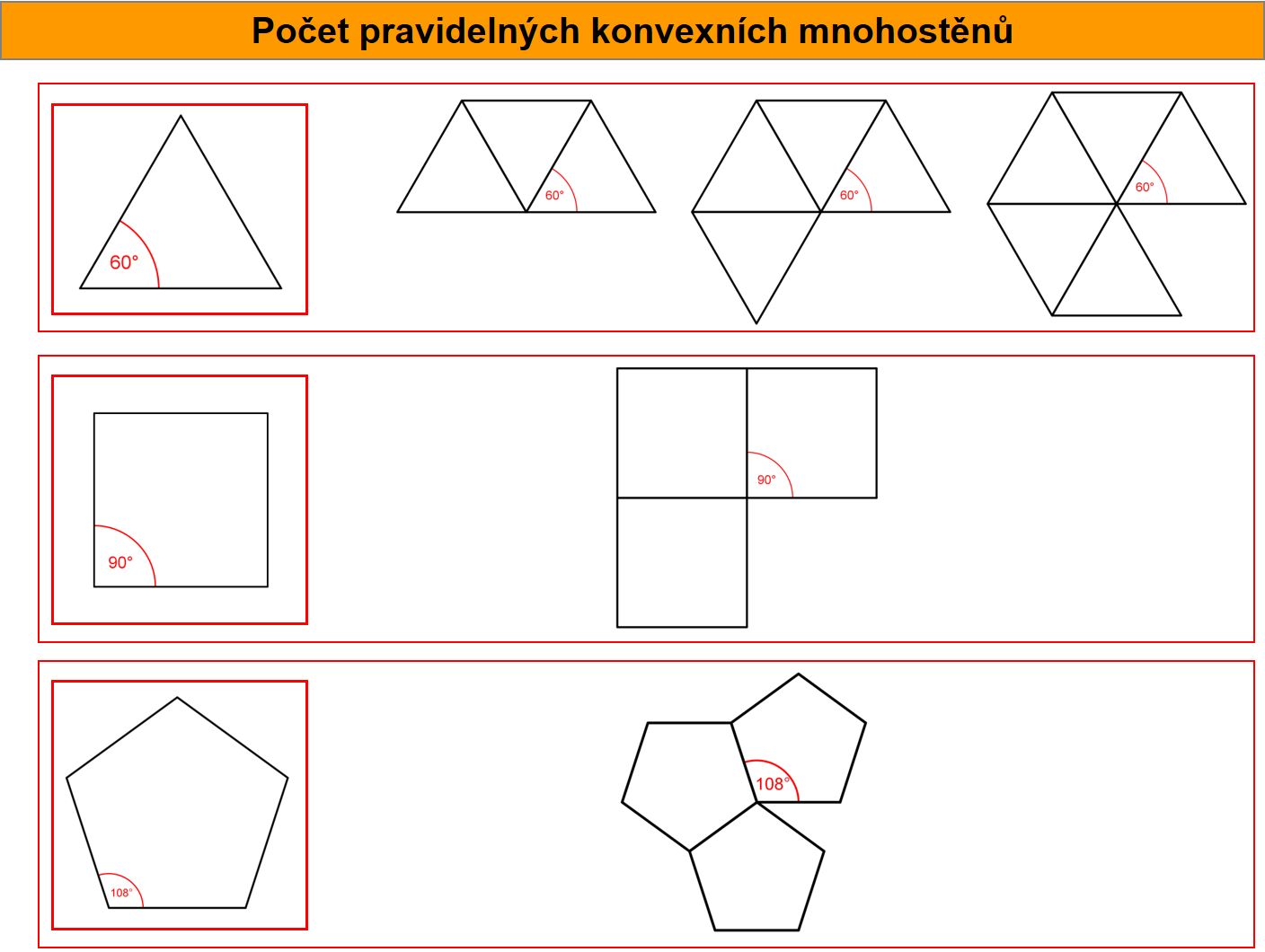
Pravidelné mnohostěny (prezentace)
Wikipedia: Platonic solid, Wikipedia: Regular polyhedra
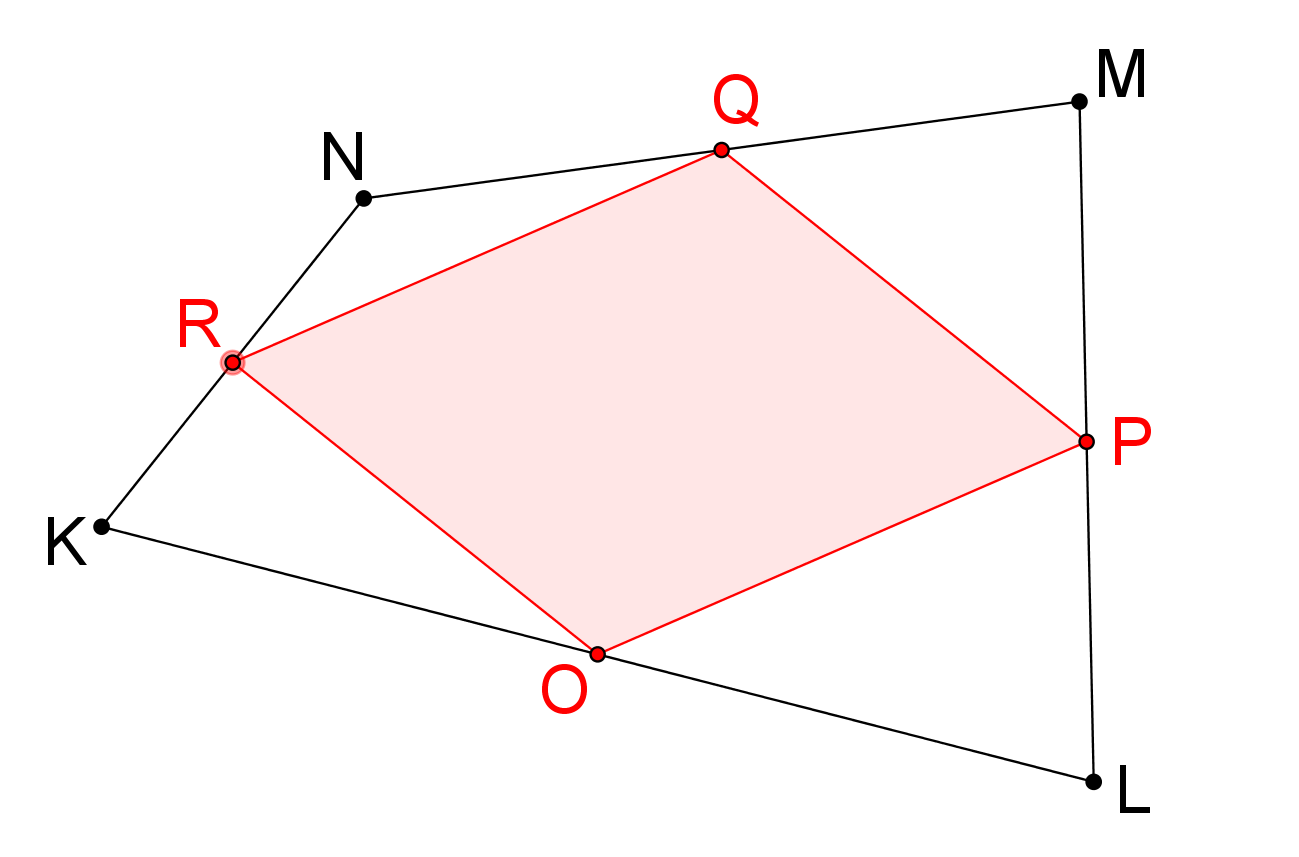
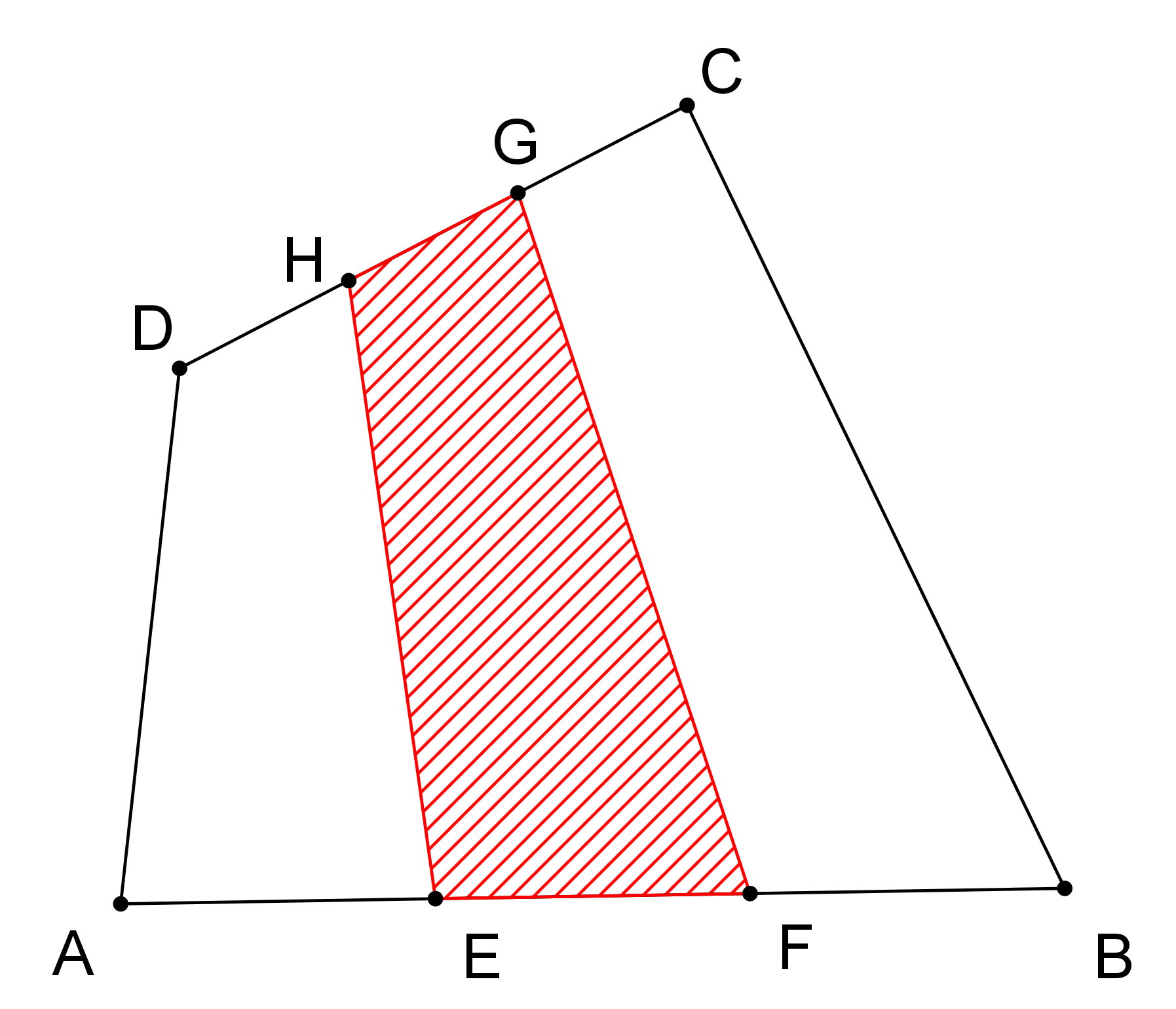
Prémiový úkol č. 4: Jakou částí obsahu čtyřúhelníku ABCD je obsah čtyřúhelníku EFGH, viz obrázek, jestliže |AE|=|EF|=|FB| a |DH|=|HG|=|GC|? Své tvrzení dokažte!
CVIČENÍ 4 -
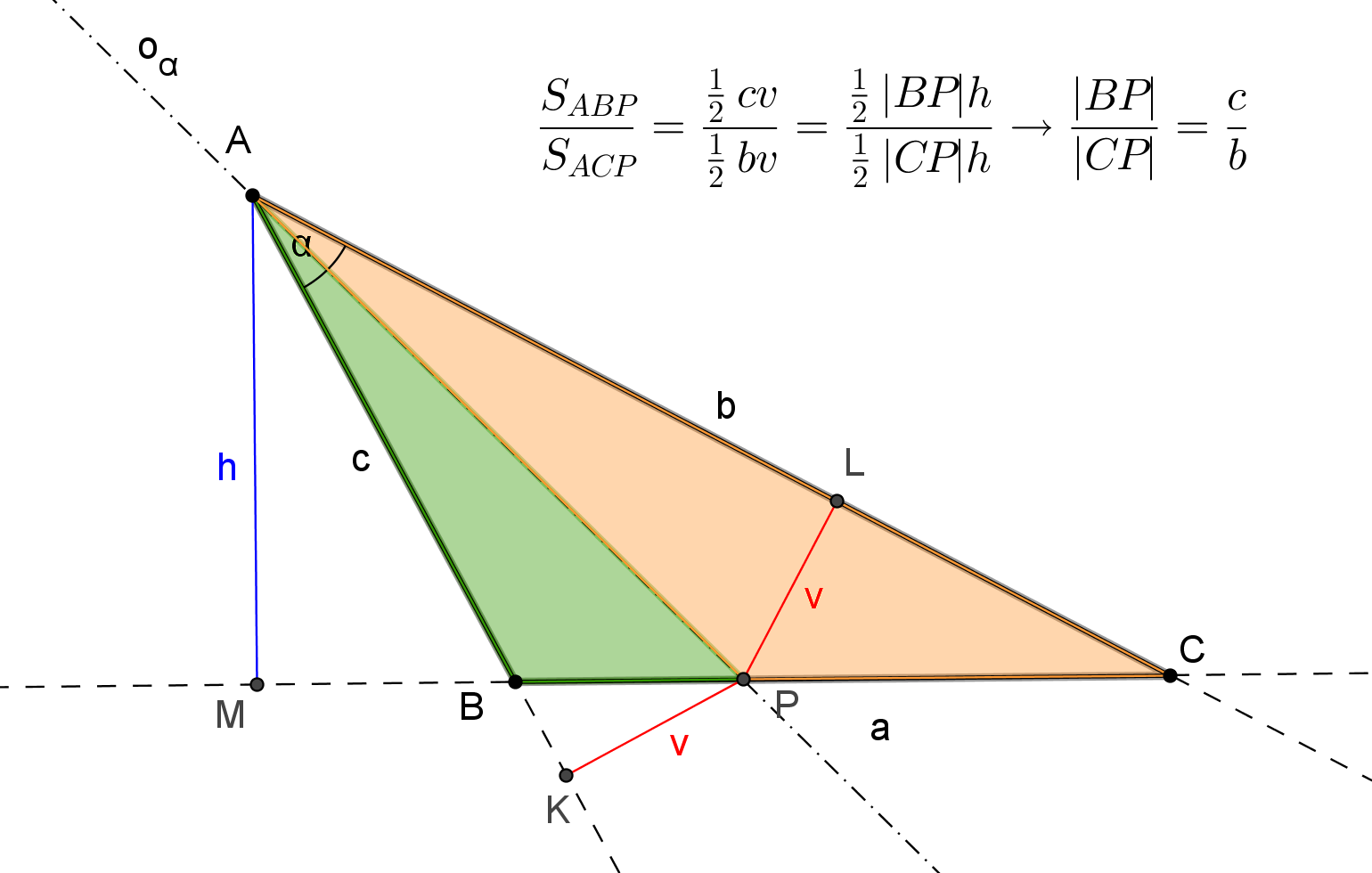
ÚKOL: Dokažte větu "V každém trojúhelníku dělí osa libovolného vnitřního úhlu protější stranu v poměru stran přilehlých."
-
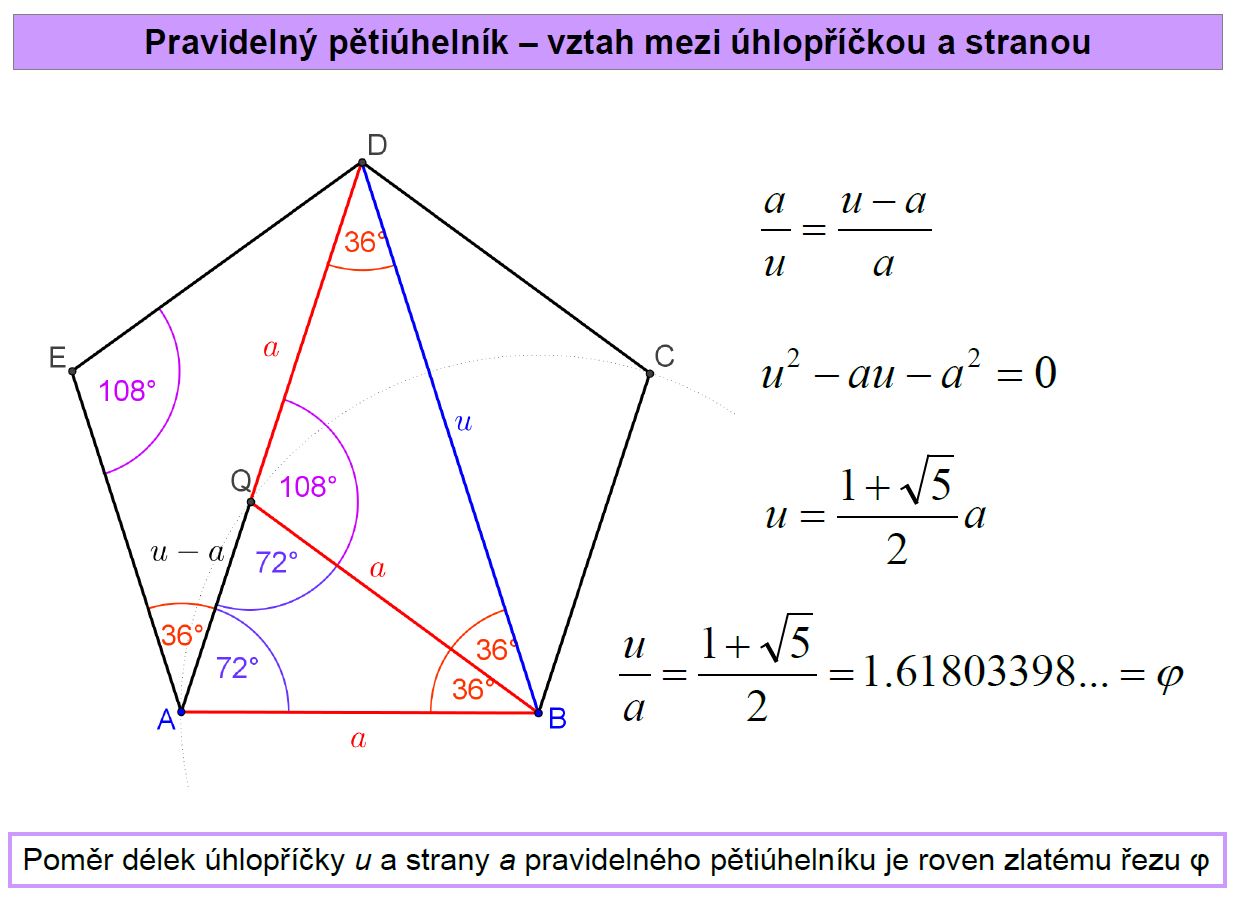
Vybrané vlastnosti pravidelných mnohoúhelníků (počet úhlopříček, velikost vnitřního úhlu, dláždění, zlatý řez)

-
Zlatý řez
Konstrukce zlatého řezu
- Cavalieriho princip
-
Objem koule
Odvození vztahu pro výpočet objemu koule užitím Cavalieriho principu (GeoGebra)
Příklady k řešení: Cvičení 4 [Řešení (viz úlohy 9 až 16)]
ÚKOL č. 4: Řešte úlohu z maturitního testu z matematiky z jara 2015: Papírová čepice má tvar rotačního kužele. Po straně je slepena lepicí páskou. (Okraje papíru jsou k sobě přiloženy a v místě lepení se nepřekrývají.) Osovým řezem kužele je rovnostranný trojúhelník s délkou strany 16 cm. Kolik cm2 papíru je použito na čepici?
Zdroj: iDNES.cz (11. 5. 2015) (zadání úlohy a diskuse nejednoznačnosti jejího zadání) - hranol, jehlan, kvádr, krychle, rovnoběžnostěn
- Pravidelné mnohoúhelníky.
-
Stereometrie. Zobrazení trojrozměrného útvaru v rovině.
PŘEDNÁŠKA 5 
14. 3. ... Pi DayZobrazení trojrozměrného útvaru v rovině
Úvod do geometrie (2019), str. 88-95.
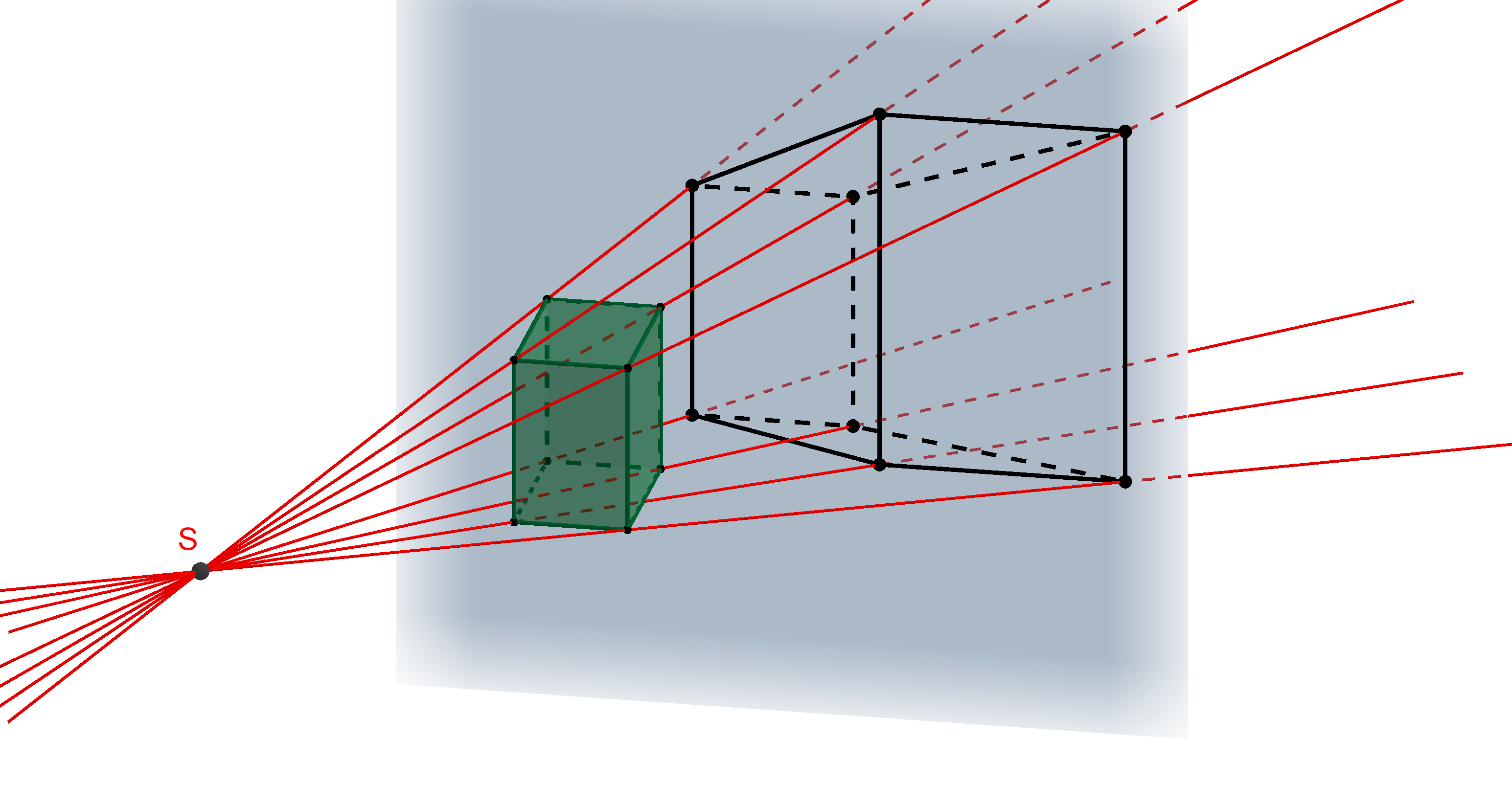
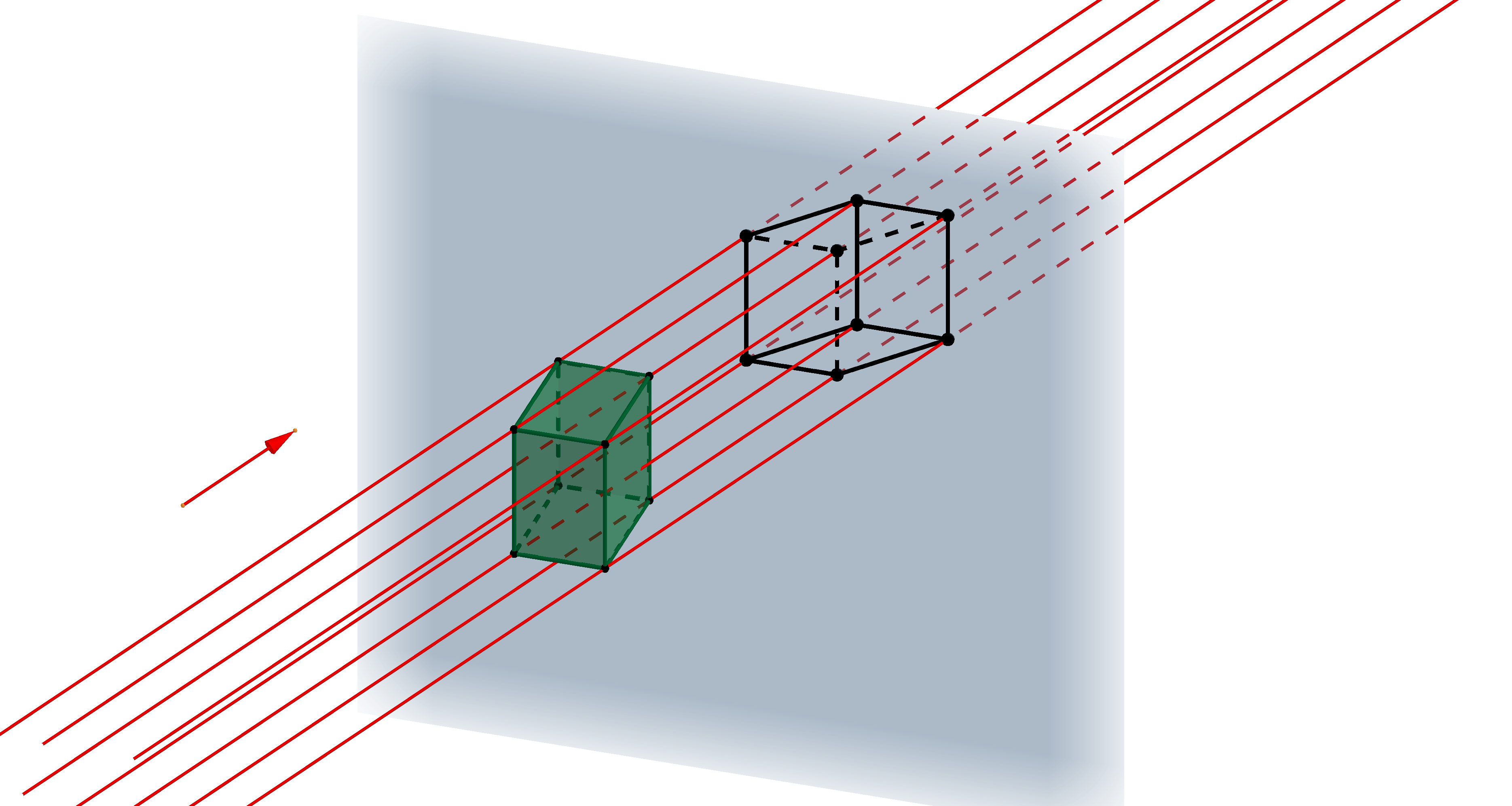
Středové promítání Rovnoběžné promítáníNázorné promítání
perspektiva pravoúhlá axonometrie kosoúhlé promítání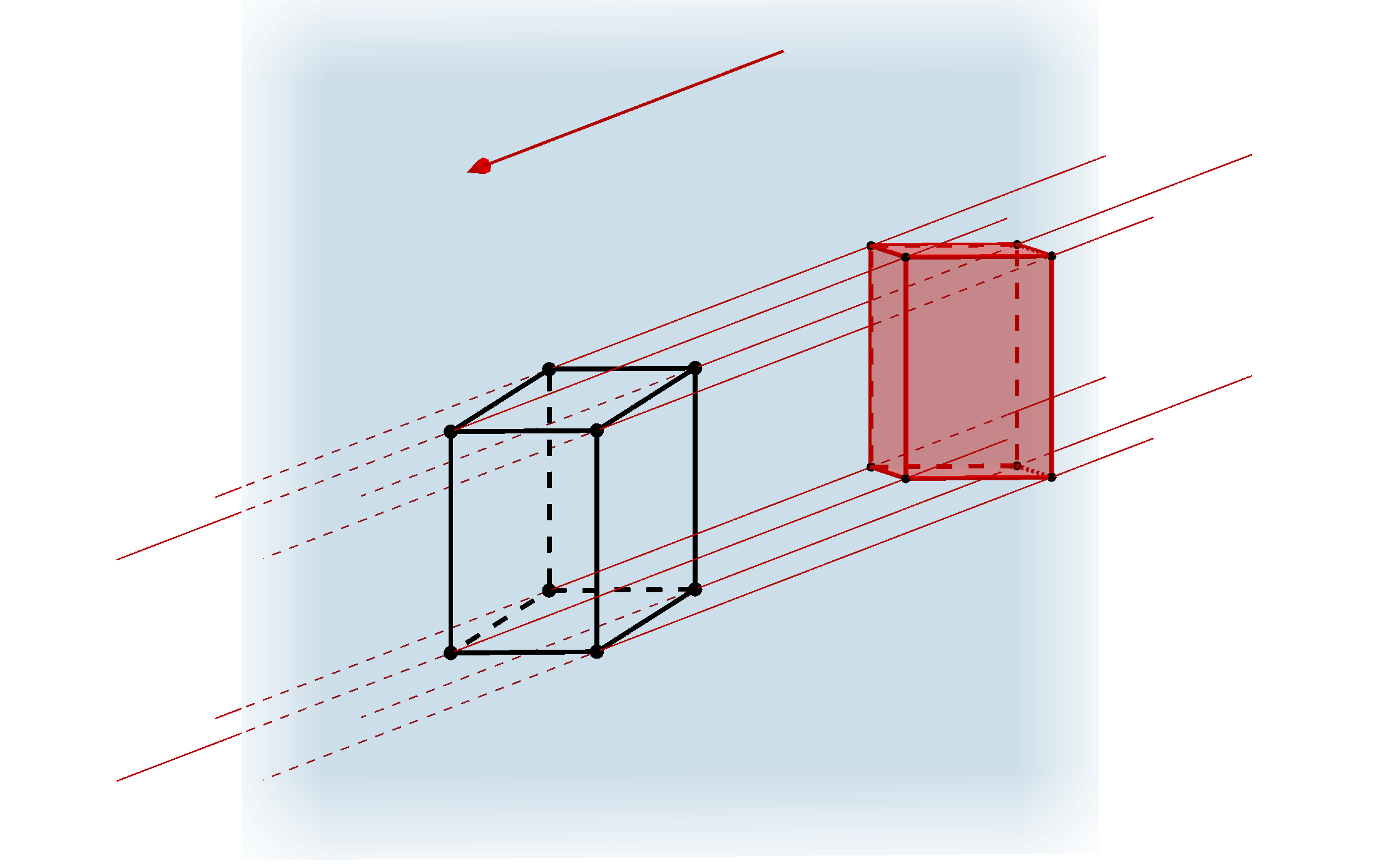
Otázka: Je pro zobrazení všech těles na následujícím obrázku použito stejné promítání?
LN: Matematika pro páťákySdružené průměty
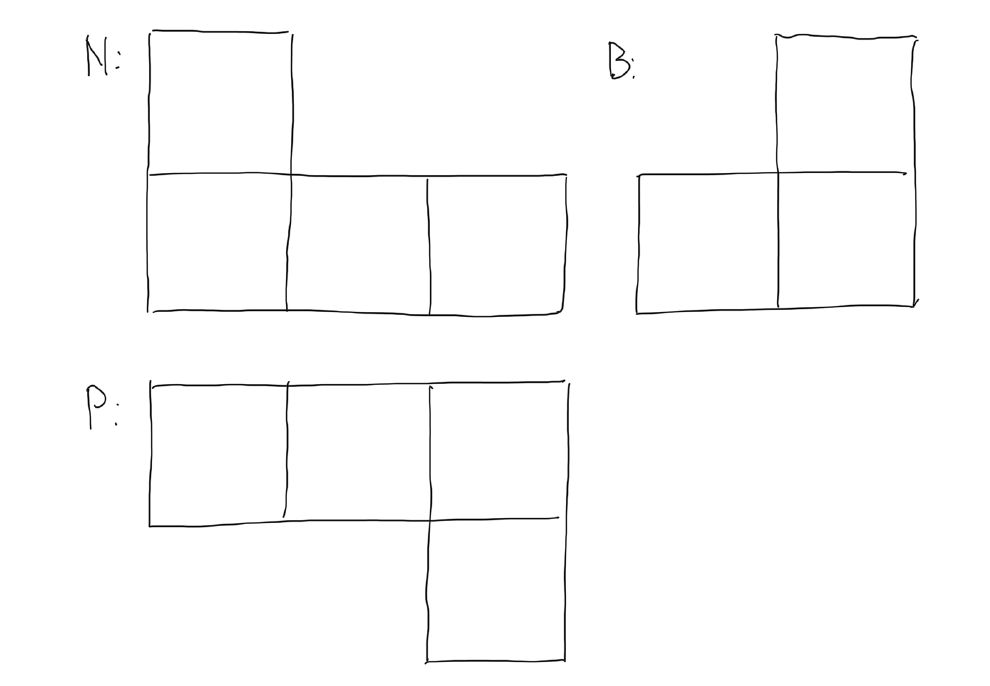
nárys, půdorys a bokorys
Stavba z krychlí
Úvod do geometrie (2019), str. 94ÚKOL: Načrtněte sdružené průměty, tj. nárys, půdorys a bokorys, pro následující stavbu z krychlí.




Pohledy pro "nárys" - "půdorys" - "bokorys"Řešení:
ÚKOL: Z krajních bodů úsečky AB jsou opsány oblouky o poloměru |AB|, které se protínají v bodě C, viz obrázek. Určete na oblouku CA bod M a na oblouku BC bod N tak, aby MN || AB a úhel NAM se rovnal danému ostrému úhlu α.
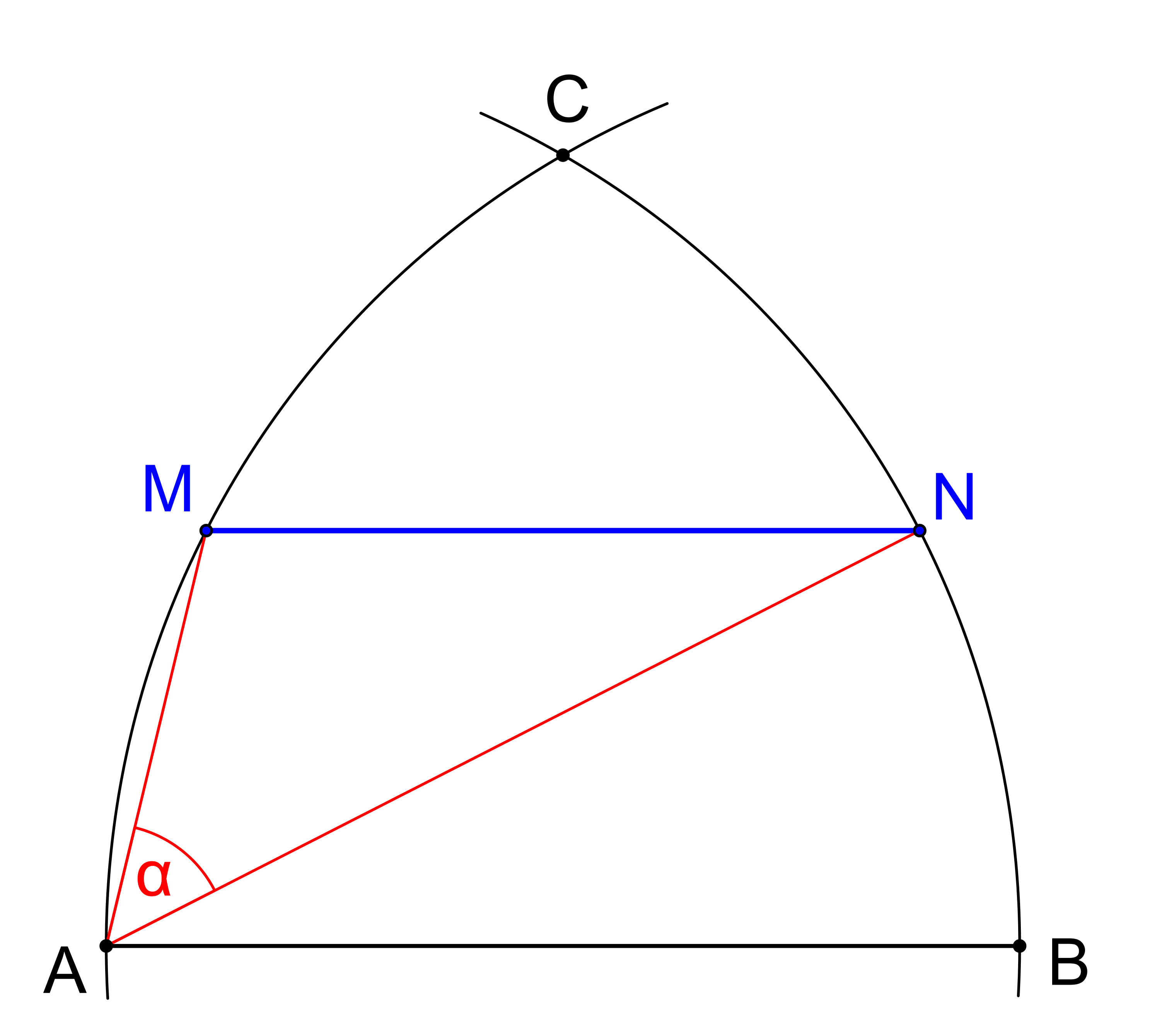
Upozornění: Úlohu je třeba řešit tak, jako by byla hodnota úhlu α předem dána! Není možné dospět konstrukcí k nějakému úhlu a potom říci, že to je ten úhel α.Řešení: Tento úkol zadal v roce 1902 Josef Rudolf Vaňaus čtenářům Časopisu pro pěstování mathematiky a fysiky (ročník 31, číslo 3), viz Časopis pro pěstování mathematiky a fysiky, vol. 31 (3), Úloha 36, str. 262. Úspěšní řešitelé, spolu s jejich řešeními, byli potom uvedeni v 5. čísle téhož ročníku, viz Časopis pro pěstování mathematiky a fysiky, vol. 31 (5), str. 471-474.
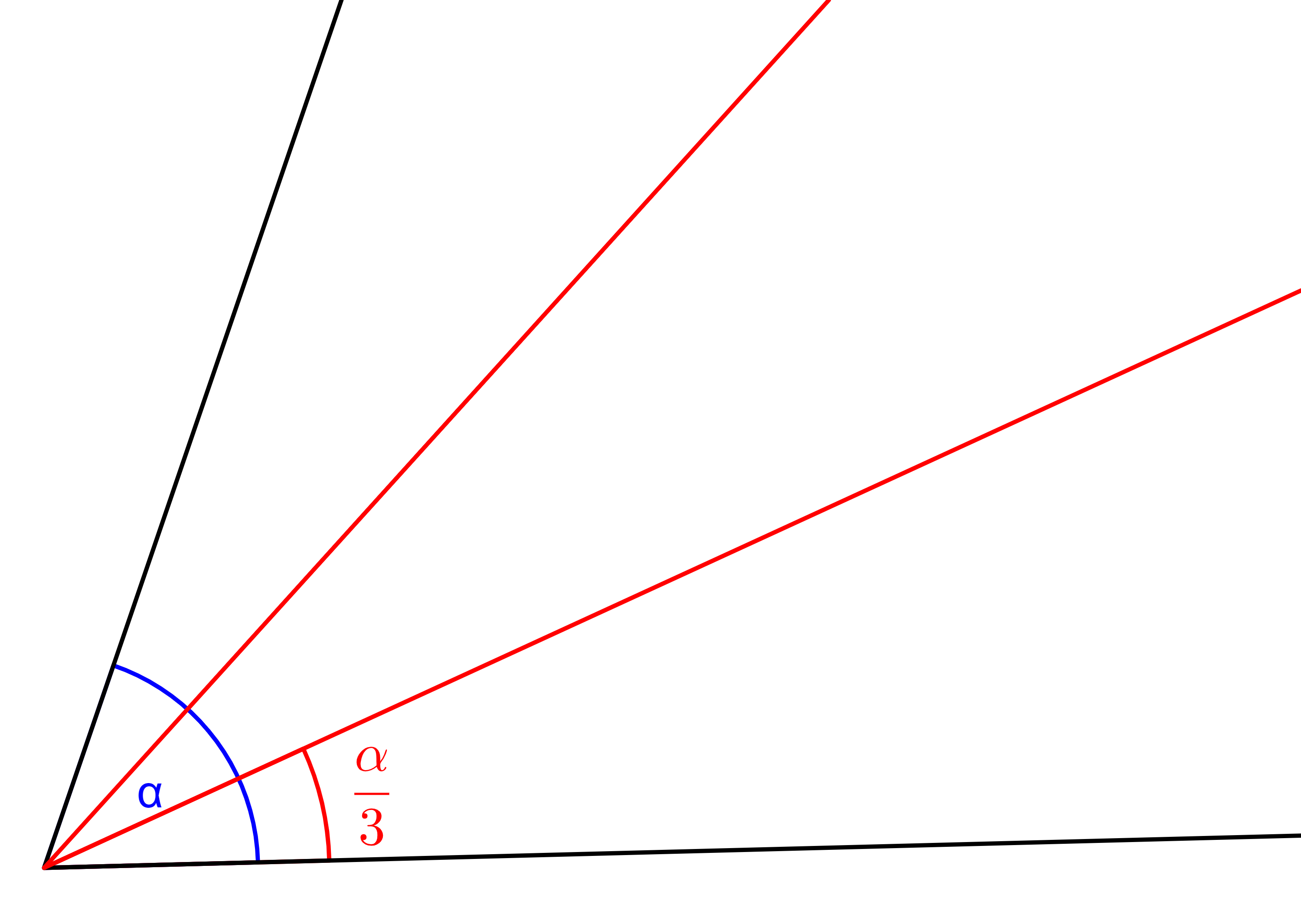
Pro vyřešení tohoto úkolu je třeba sestrojit třetinu známého úhlu, jak je vidět z výpočtu naznačeného v tomto materiálu: GeoGebra: Vaňausův Problém 36. Úkol sestrojit rozdělit daný úhel na tři stejné části, zvaný též trisekce úhlu, není možné vyřešit eukleidovsky, tj. pouze užitím pravítka a kružítka!
Trisekce úhlu
Trisekce úhlu patří mezi tři klasické problémy trisekce úhlu, kvadratura kruhu a zdvojení krychle, které nelze vyřešit eukleidovsky, tj. použitím pravítka a kružítka;
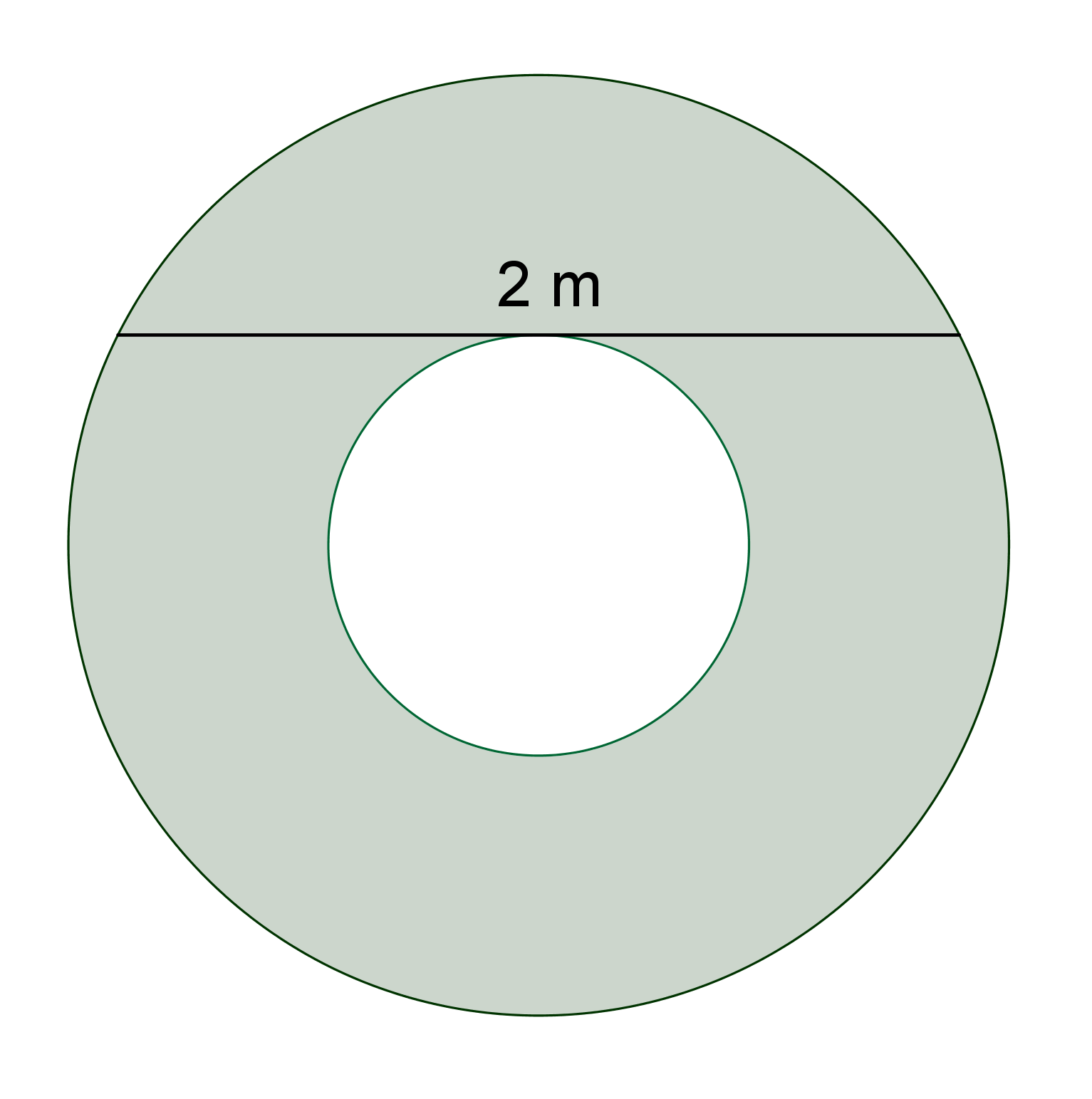
Prémiový úkol č. 5: Určete velikost vybarveného mezikruží, je-li délka tětivy tečné k jeho vnitřní hraniční kružnici 2 m, viz obrázek.
CVIČENÍ 5 ÚKOL č. 5: Načrtněte nárys, půdorys a bokorys pro každou z níže zobrazených staveb z krychlí!



Úkol: Kolik různých krychlových těles (tvarů) můžeme vytvořit ze čtyř krychlí?
Tvary ze čtyř krychlí (GeoGebra applet) Polycube
Wolfram MathWorld: Polycube
Wolfram MathWorld: PolyonimoSoma cube Wikipedia: Soma cube
-
Planimetrie. Symetrie roviny. Geometrická zobrazení.
PŘEDNÁŠKA 6 Symetrie roviny
Úvod do geometrie (2019), str. 58.








YouTube: Symmetry in Geometry
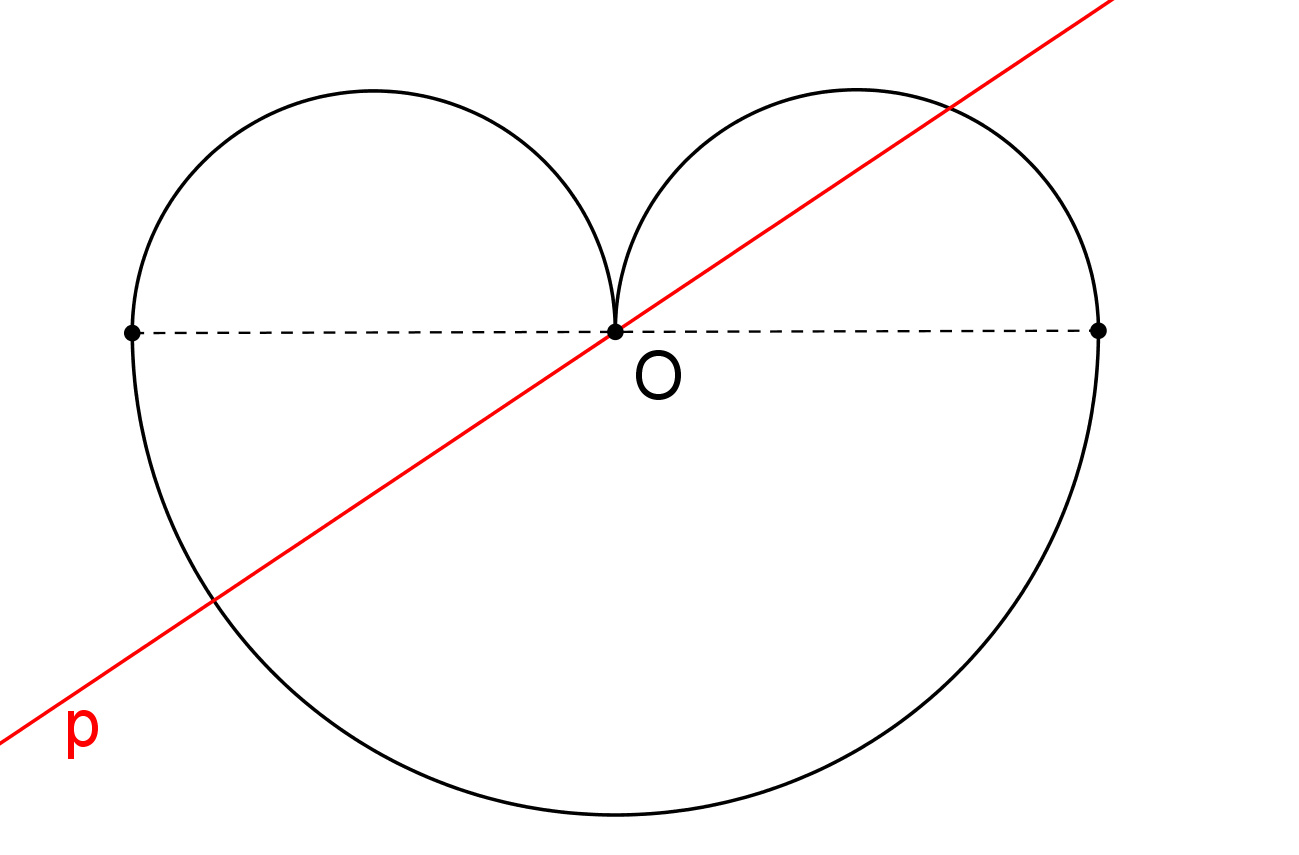
Prémiový úkol č. 6: Na obrázku vidíme obrazec, který vznikne spojením větší půlkružnice s dvěma menšími stejně velkými půlkružnicemi. Dokažte, že každá přímka p jdoucí bodem O rozděluje obvod tohoto obrazce na dvě stejné části!
CVIČENÍ 6 ÚKOL č. 6: Dokažte Vivianiho větu: Součet vzdáleností libovolného bodu v rovnostranném trojúhelníku od jeho stran je roven výšce tohoto trojúhelníku.
Příklad: Je dána přímka p a body A, B v téže polorovině s hraniční přímkou p. Najděte všechny body X ∈ p takové, že součet vzdáleností |AX|+|BX| je minimální. (tzv. Heronův problém; Hérón Alexandrijský, přibl. 10-70 n.l.)
ÚKOL č. 6: Sestrojte trojúhelník, je-li dáno:
- a, va, γ,
- a, b, ta,
- a, b, tc,
- a, b, vc,
- a, b, va,
- a, α, vb.
Řešení: Rozbor, postup konstrukce a diskuse (úterý 6. 4.) / Rozbor, postup konstrukce a diskuse (čtvrtek 8. 4.)
-
Osová souměrnost. Skládání geometrických zobrazení.
PŘEDNÁŠKA 7 Shodnosti v rovině. Osová souměrnost. Středová souměrnost. Skládání geometrických zobrazení.
Úvod do geometrie (2019), str. 65-73. Planimetrie (2020), str. 46-62.
Shodná zobrazení v rovině
Geometrické zobrazení v rovině: Geometrickým zobrazením v rovině rozumíme předpis, kterým je každému bodu X roviny (říkáme mu vzor) přiřazen právě jeden bod Y téže roviny (říkáme mu obraz).
[Osová souměrnost] [Otočení] [Středová souměrnost] [Posunutí] [Posunutá souměrnost] ÚKOL: Vysvětlete pojmy samodružný bod, samodružná přímka, samodružný směr. Uveďte konkrétní příklady s využitím shodností v rovině.
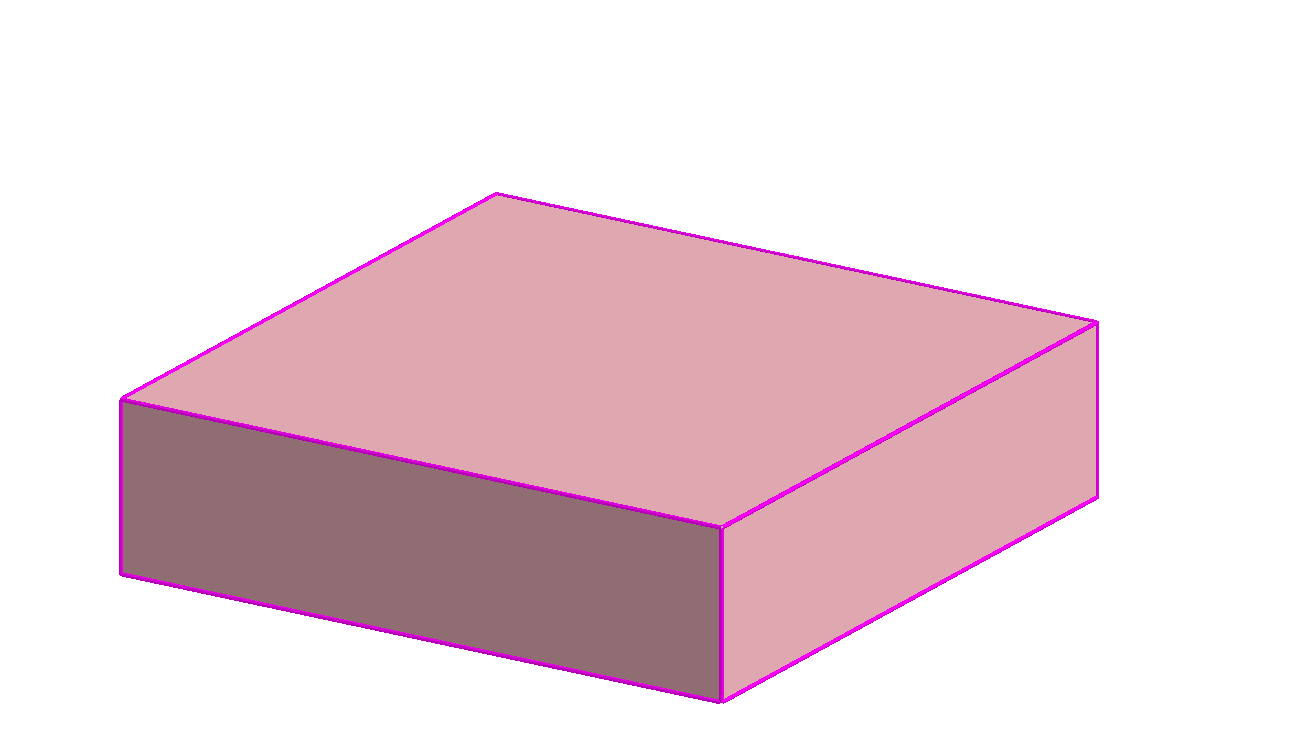
Prémiový úkol č. 7: Dort ve tvaru kvádru s čtvercovým půdorysem je po stranách a nahoře pokryt marcipánovým potahem, viz obrázek. Navrhněte postup, jak tento dort rozdělit na 7 dílů téhož objemu tak, aby každý obsahoval stejné množství chutného potahu.
CVIČENÍ 7 ÚKOL: Vysvětlete pojmy samodružný bod, samodružná přímka, samodružný směr. Uveďte konkrétní příklady s využitím shodností v rovině.
Osová souměrnost / Středová souměrnost / Otočení / Posunutí / Posunutá souměrnost
Osová souměrnost
Příklad: Sestrojte trojúhelník ABC, je-li dán jeho obvod o = 12 cm a úhly α = 60°, β = 45°.
Rozbor příkladu (iPad - poznámky) / Rozbor příkladu (GeoGebra)
Středová souměrnost
Příklad: Je dán trojúhelník ABC a jeho vnitřní bod M. Sestrojte všechny úsečky XY se středem M a s krajními body X, Y na hranici trojúhelníku.
Řešení:
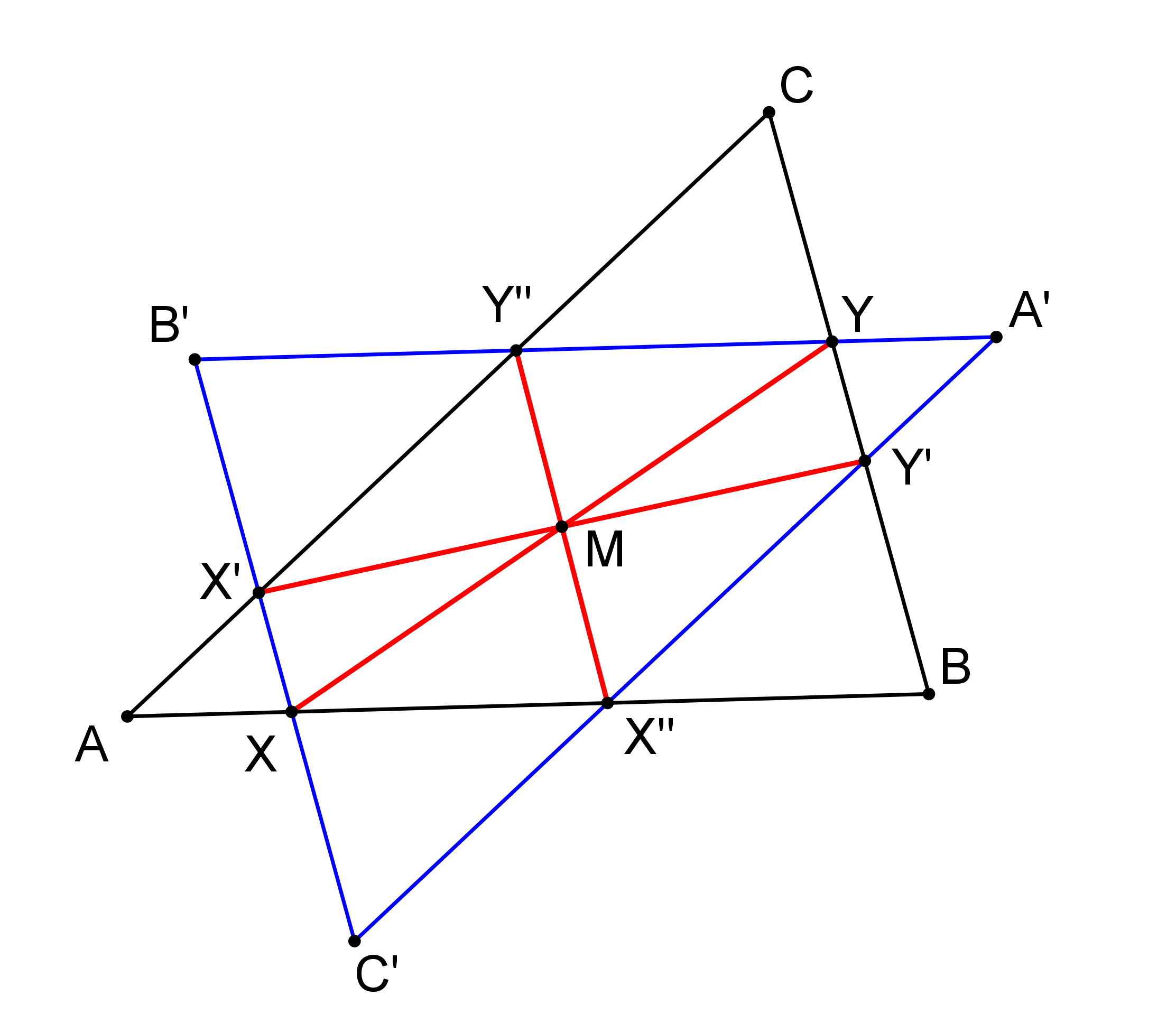
[GeoGebra applet]
Detailní popis řešení příkladu je uveden v textu Hašek, R. Planimetrie na str. 59.Geogebra Classroom
Řešte výše uvedené příklady v prostředí GeoGebra Classroom
Skládání zobrazení
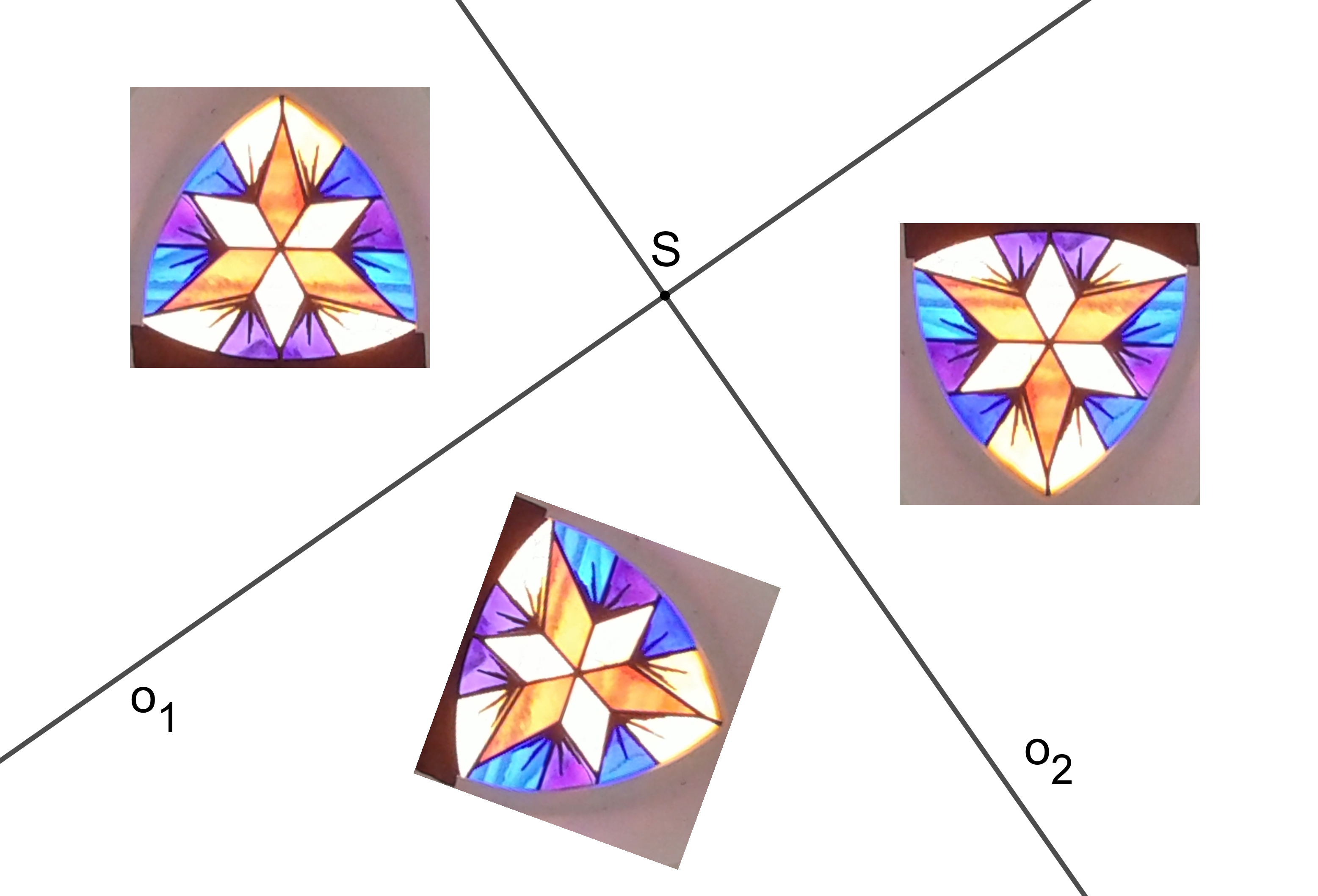
[GeoGebra applet]GeoGebra: Skládání dvou osových souměrností
ÚKOL č. 7: Sestrojte lichoběžník ABCD, je-li dáno:
- a, c, α, β
- a, b, c, d,
- b, c, d, α-β.
Řešení: Rozbor a postup konstrukce
Prémiový úkol č. 8: Rovnostranný trojúhelník ABC o dělce strany 4 cm otočíme kolem jeho průsečíku výšek o 90°, dostaneme tak trojúhelník A'B'C', viz obrázek. Určete obsah průniku trojúhelníků ABC a A'B'C'.
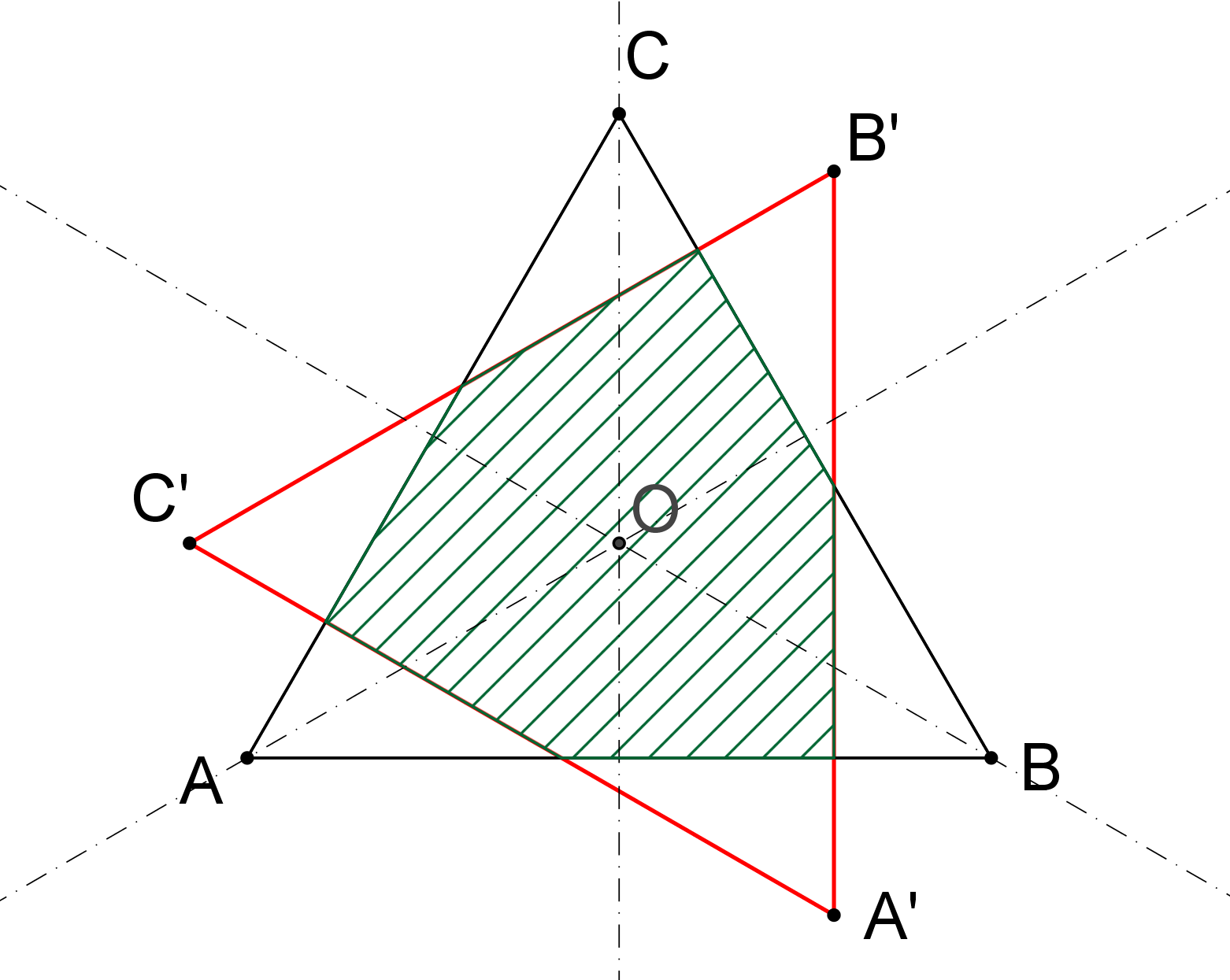
CVIČENÍ 8 ÚKOL č. 8: Sestrojte trojúhelník ABC, je-li dáno:
- a, α, va,
- a, α, ta,
- a, α, ρ (ρ je poloměr kružnice vepsané trojúhelníku ABC).
Řešení: Rozbor a postup konstrukce (úterý 13. 4.) / Rozbor a postup konstrukce (čtvrtek 15. 4.)
PŘEDNÁŠKA 9 Úsekový úhel
Úsekový úhel příslušný k oblouku AB kružnice, viz obrázek, je úhel, jehož jedním ramenem je polopřímka AB a druhým ramenem je polopřímka AX, kde X je bod tečny ke kružnici v bodě A volený tak, aby oblouk AB byl částí úhlu BAX. (Terminologická komise JČMF. (1981) Slovník školské matematiky. Praha: Státní pedagogické nakladatelství.)
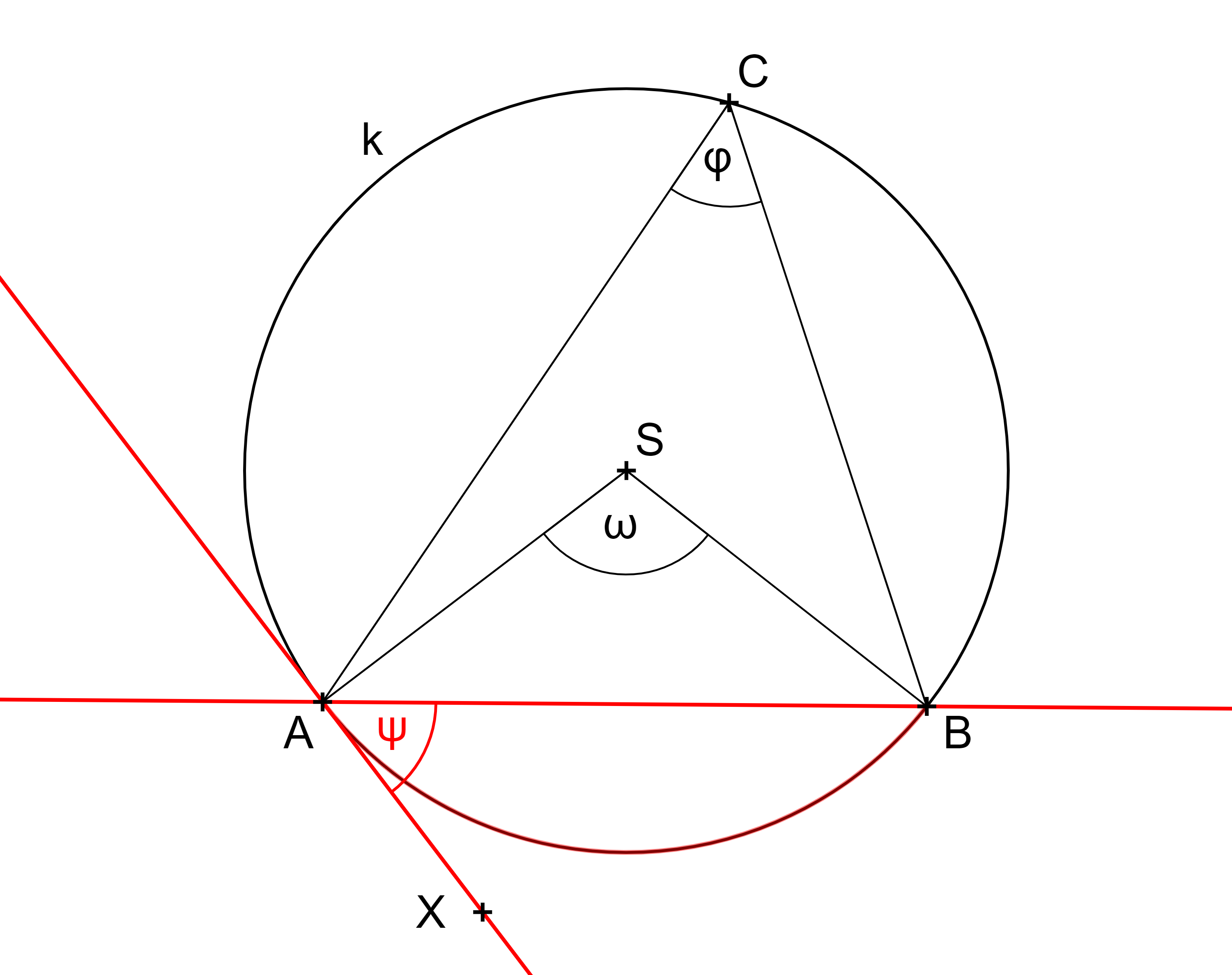
ÚKOL: Jaký je vztah mezi velikostmi úhlů φ, ω a ψ, tj. mezi velikostmi obvodového, středového a úsekového úhlu příslušejícími témuž oblouku?
Poznámky z přednášky (úsekový úhel): 7UM2 Pr 12.04.2021.pdf
Vztah mezi velikostí obvodového a středového úhlu: Velikost obvodového úhlu příslušejícího oblouku AB je rovna polovině velikosti středového úhlu příslušejícího témuž oblouku. [GeoGebra aplet]
Množina bodů v rovině, z nichž je daná úsečka vidět pod daným úhlem
ÚKOL: Sestrojte množin všech bodů v rovině, z nichž je úsečka AB vidět pod úhlem: a) α = 30°; b) β = 150°.
Prémiový úkol č. 9: Jestliže má tětivový čtyřúhelník (tj. čtyřúhelník vepsaný do kružnice) vzájemně kolmé úhlopříčky, které se protínají v bodě E, přímka jdoucí bodem E kolmo k libovolné jeho straně půlí protilehlou stranu, viz obrázek. Dokažte!
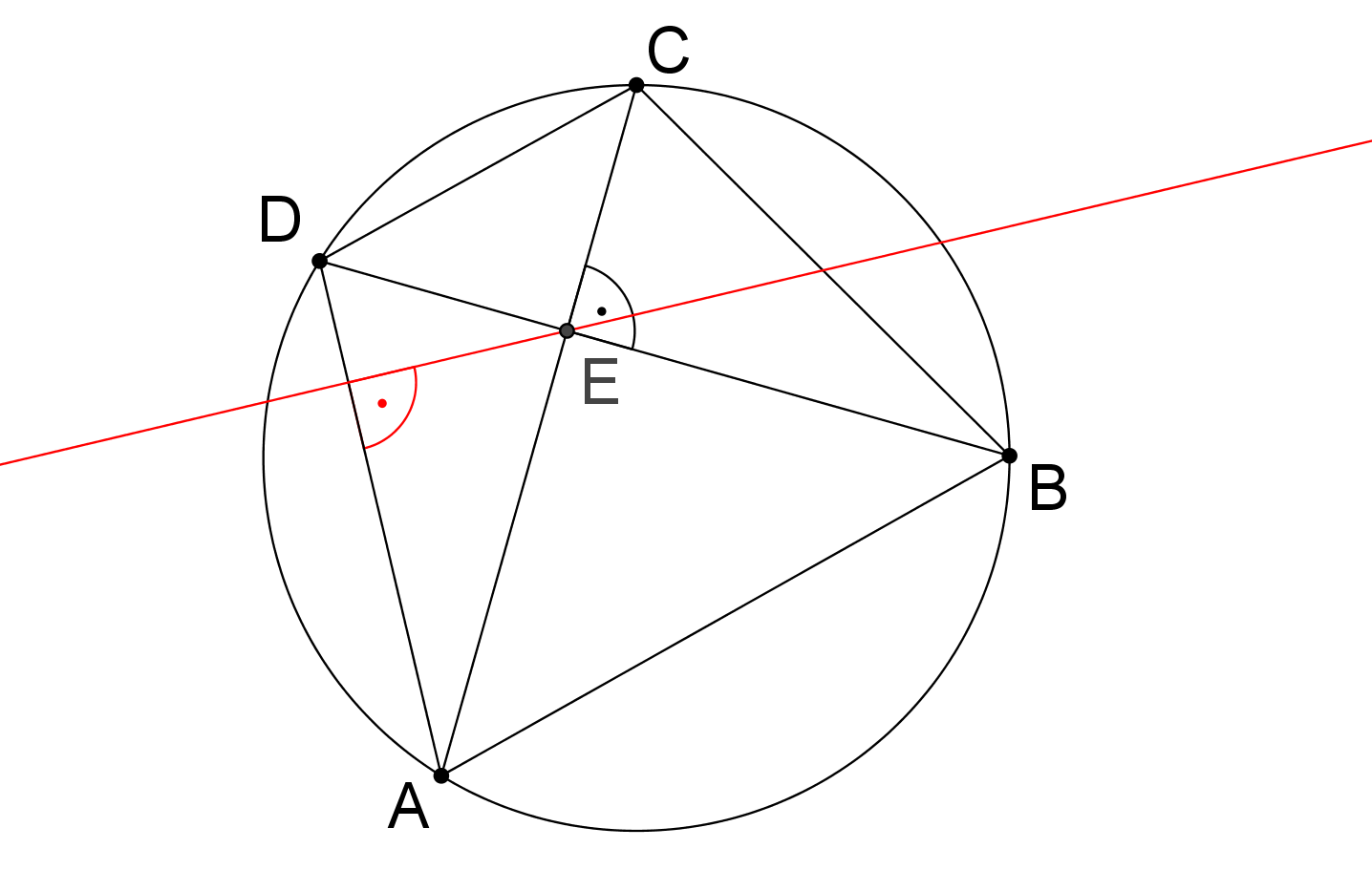
CVIČENÍ 9 ÚKOL č. 9:
a) Jsou dány body X, Y a S, viz obrázek. Sestrojte čtverec ABCD tak, aby bod X ležel na přímce AB, bod Y na přímce CD a bod S byl středem čtverce.
b) Jsou dány body X, Y a S, viz obrázek. Sestrojte čtverec ABCD tak, aby bod X ležel na přímce AB, bod Y na přímce BC a bod S byl středem čtverce.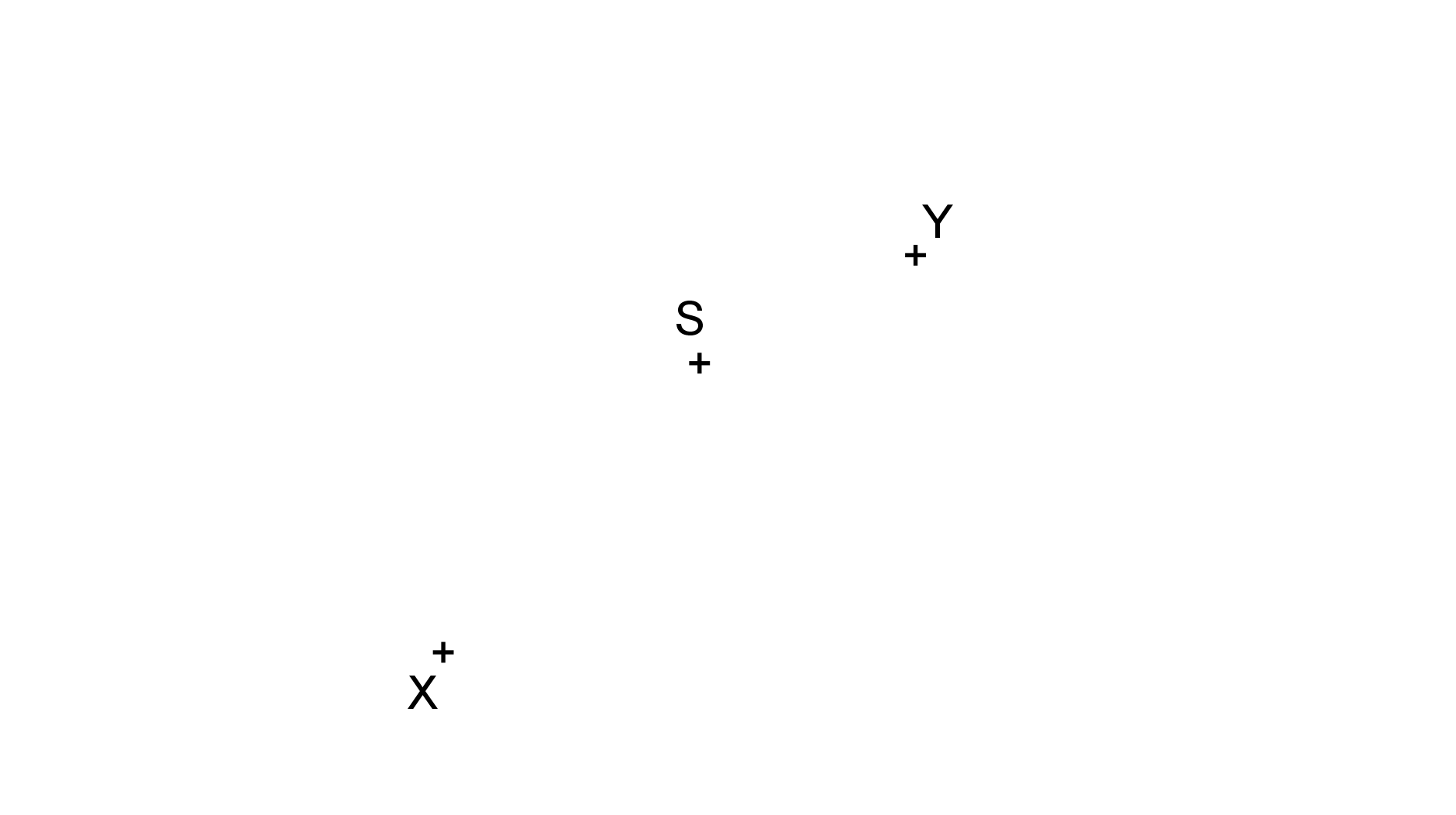
-
Posunutí. Otočení. Posunuté zrcadlení.
PŘEDNÁŠKA 10 

Prémiový úkol č. 10: Nad stranami AC a BC trojúhelníku ABC jsou sestrojeny čtverce ACDE a BFGC, viz obrázek. Potom poloha středu M úsečky EF nezávisí na umístění vrcholu C (tj. bod M nemění při pohybu bodu C svou polohu). Dokažte!
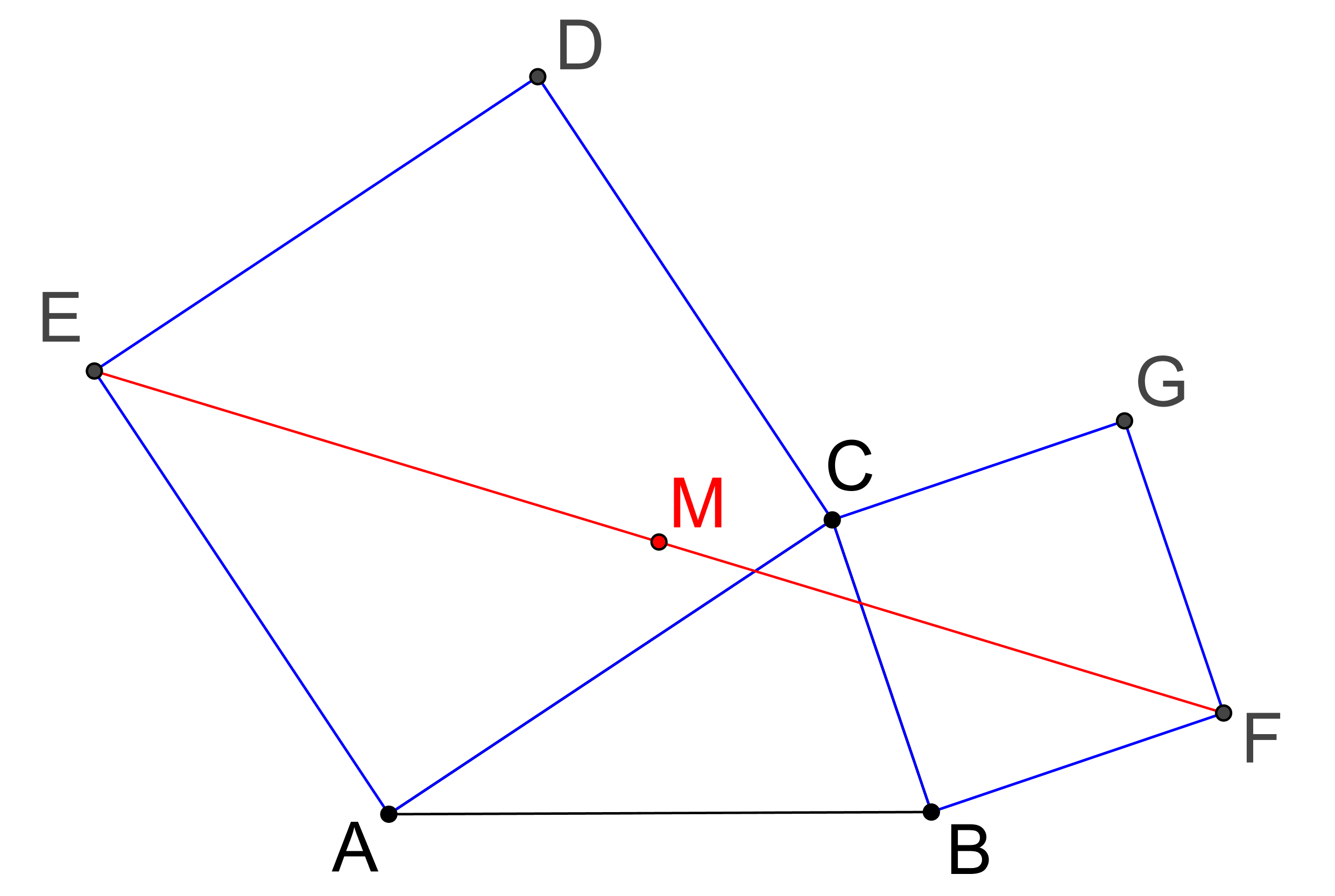
CVIČENÍ 10 Geogebra Classroom
Přihlaste se do GeoGebra Classroom s kódem, který Vám bude sdělen.
Příklad 1: Jsou dány různé rovnoběžné přímky a, b, c a bod A, který leží na přímce a. Sestrojte všechny rovnostranné trojůhelníky ABC, jejichž vrcholy B, C leží po řadě na přímkách b, c.
Příklad 2: Jsou dány kružnice k, přímka p a bod A ležící vně k. Sestrojte rovnostranný trojúhelník s vrcholem v bodě A tak, aby zbývající vrcholy ležely na k a na p.
ÚKOL č. 10: Jsou dány tři různé přímky p1, p2, p3 procházející bodem S; na přímce p1 je dán bod A různý od S. Sestrojte trojúhelník ABC, jehož osy vnitřních úhlů leží v přímkách p1, p2, p3. Proveďte rozbor úlohy náčrtkem a navrhněte postup konstrukce. Vlastní konstrukci proveďte formou online materiálu vytvořeného v GeoGebře, s případnou možností přehrát postup konstrukce krok za krokem.
-
Podobnost. Stejnolehlost.
PŘEDNÁŠKA 11 Podobné zobrazení. Podobnost.
Úvod do geometrie (2019), str. 80-83.
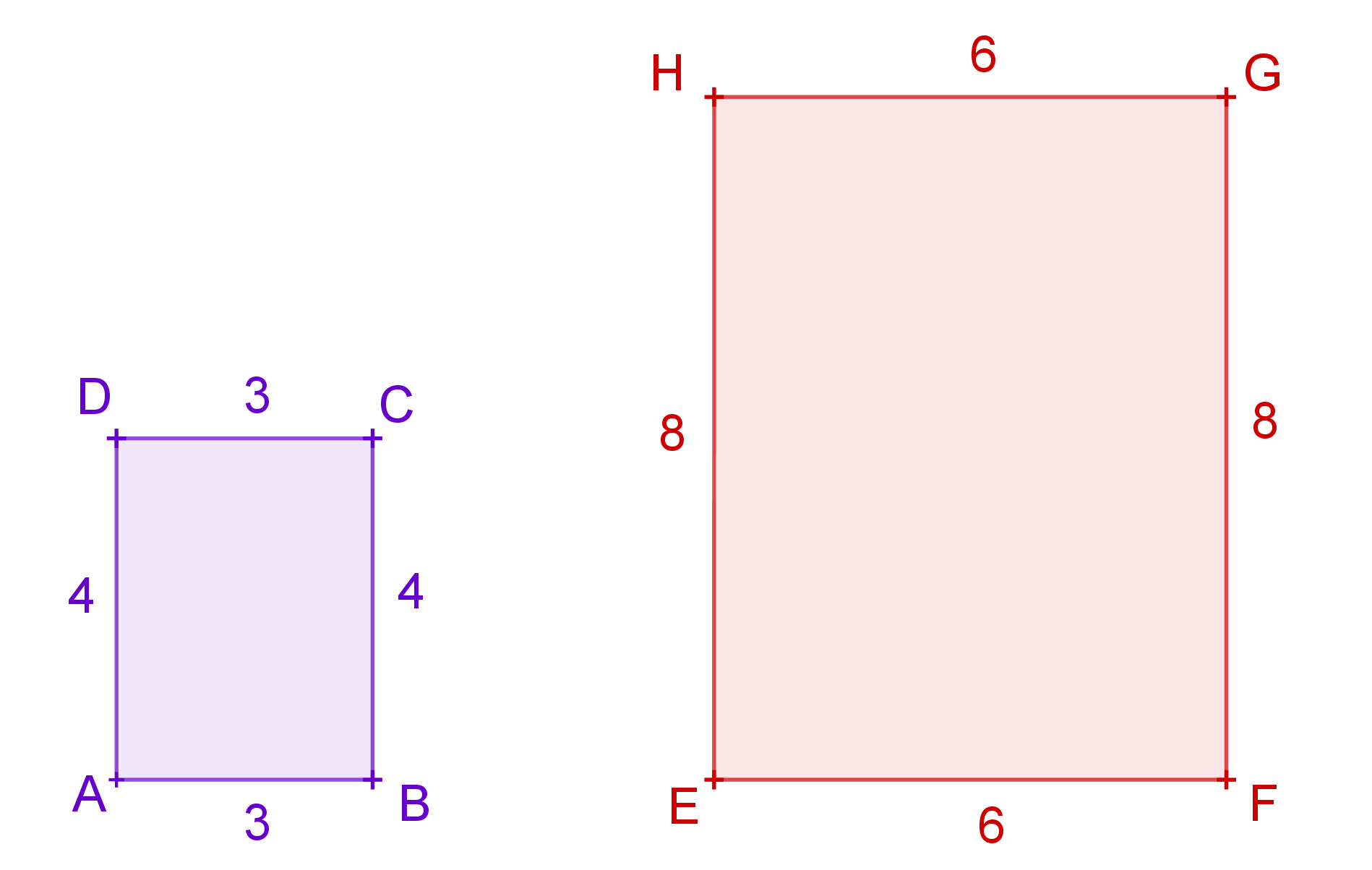
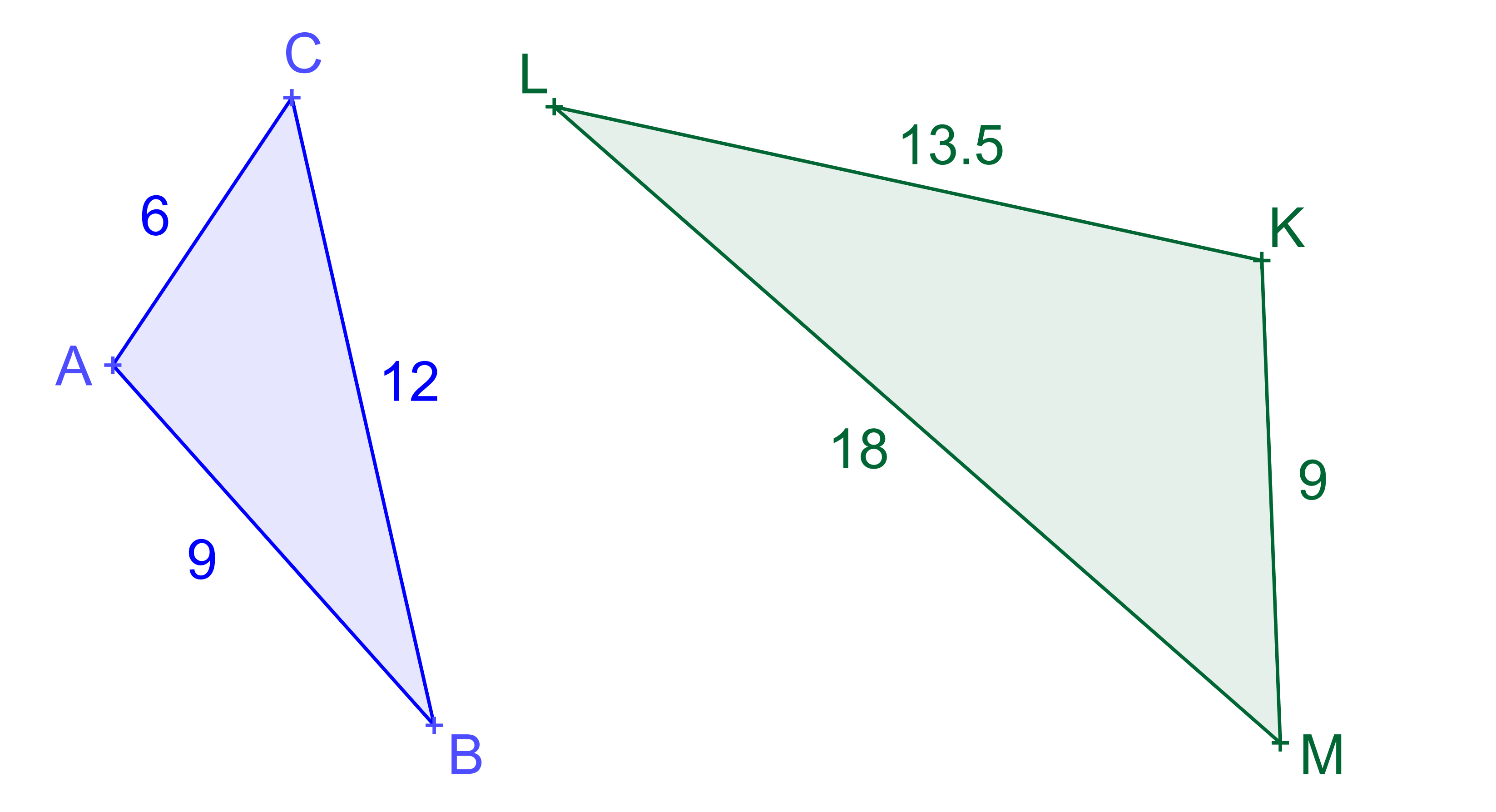
Které z dvojic útvarů jsou vzájemně shodné či podobné?
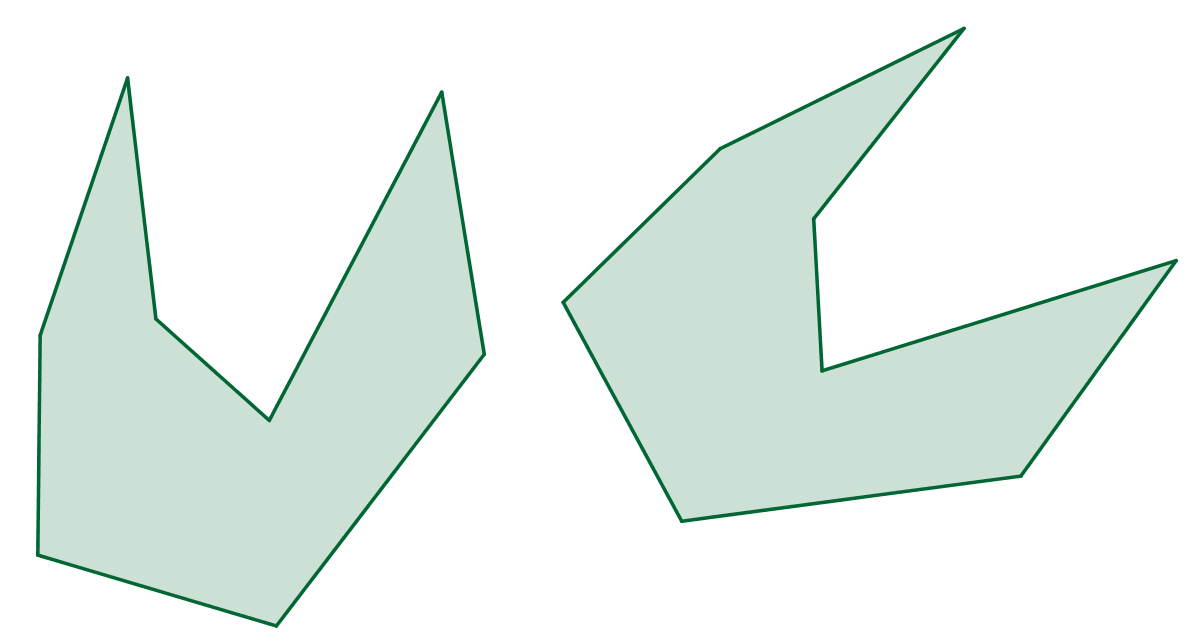
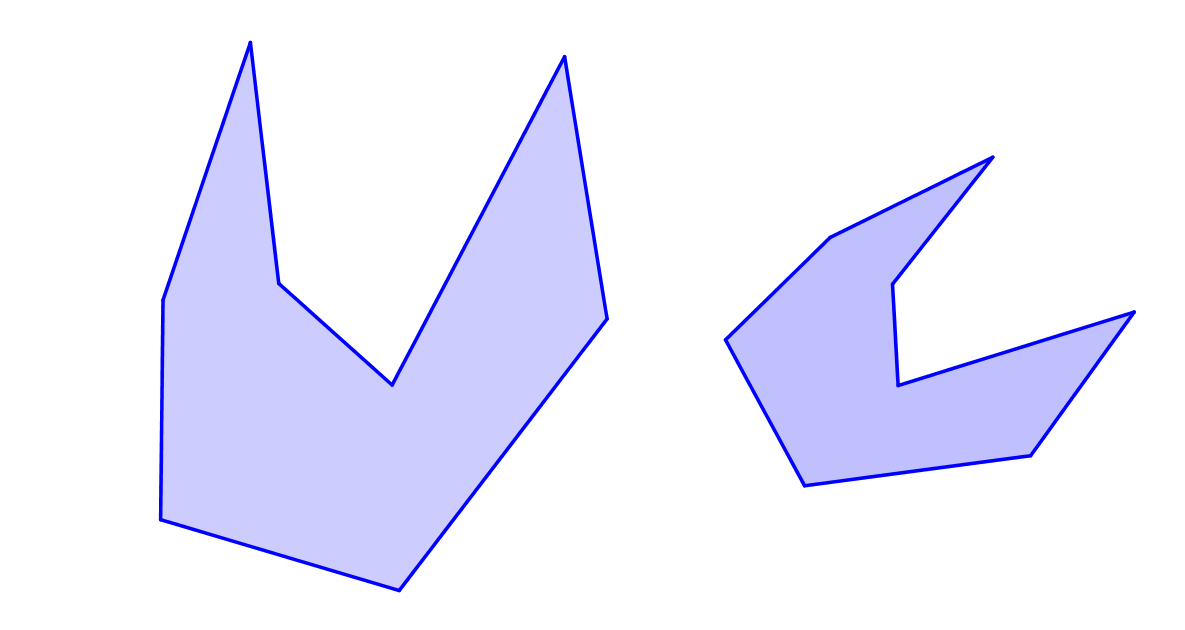
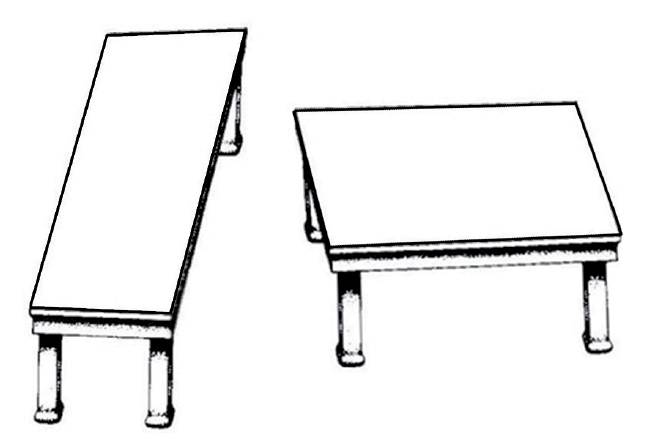
Shepard's tablesDefinice podobnosti: Podobné trojúhelníky.
Podobné útvary.
Prémiový úkol č. 11: V rovině je dán čtverec ABCD. Kružnice k prochází body A, B a dotýká se přímky CD. Označme M průsečík kružnice k a strany BC (různý od B), viz obrázek. Určete poměr |CM|:|MB|.
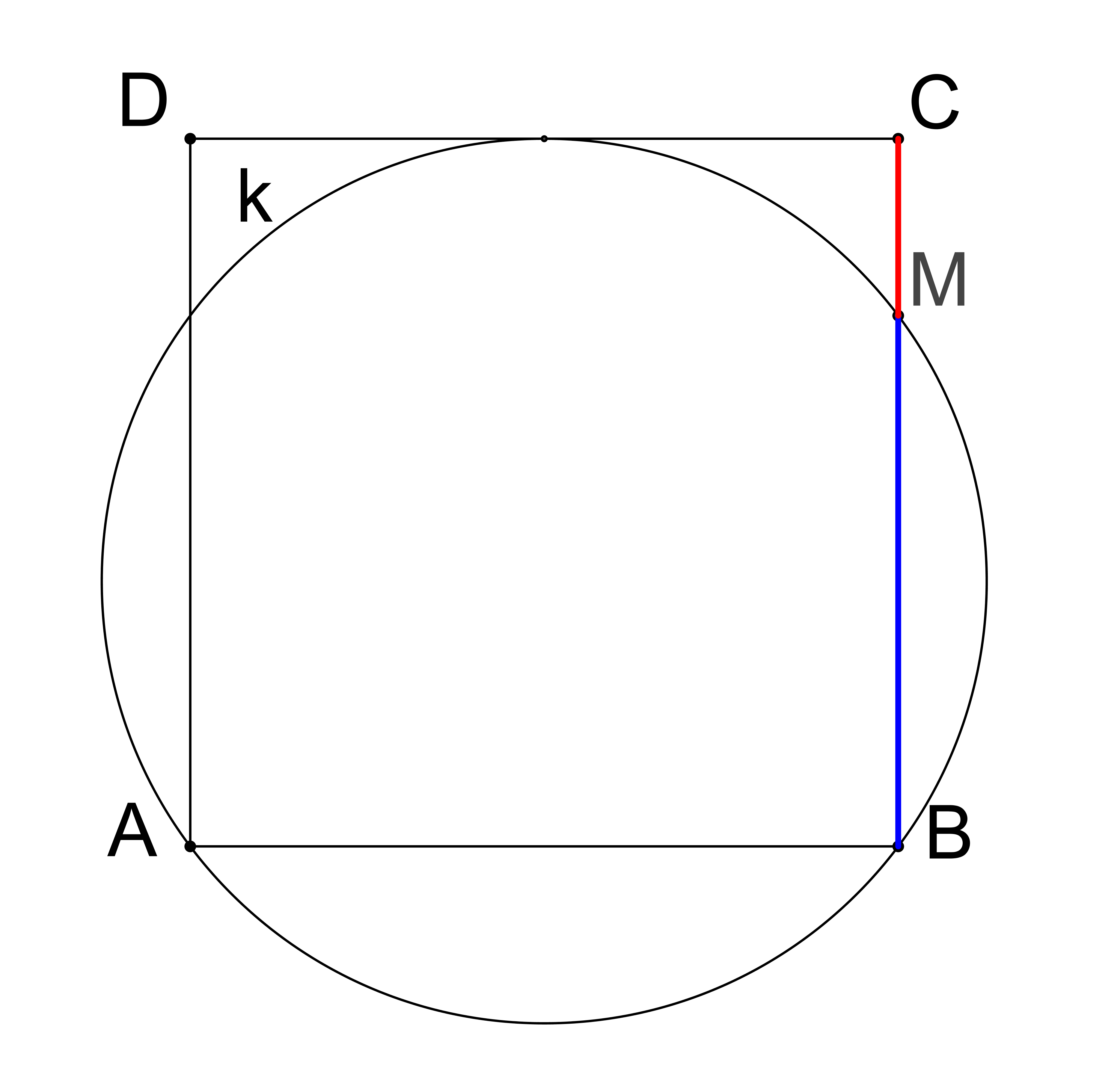
CVIČENÍ 11 Příklad 1: Sestrojte alespoň jeden trojúhelník ABC, pro který platí |AB|:|AC| = 3:5, α = 60°, ρ = 1,8 cm (poloměr kružnice vepsané).
Řešení: GeoGebra applet
Detailní popis řešení příkladu je uveden v textu Hašek, R. Planimetrie na str. 104.Příklad 2: Sestrojte kosodélník ABCD, je-li dáno |∠DAB| = α, |∠ABD| = ε, |AC| = e.
Řešení: GeoGebra applet
Věty o shodnosti trojúhelníků
Detailní popis řešení příkladu je uveden v textu Hašek, R. Planimetrie na str. 105.sss, sus, usu, Ssu
Věty o podobnosti trojúhelníkůsss, sus, uu, Ssu
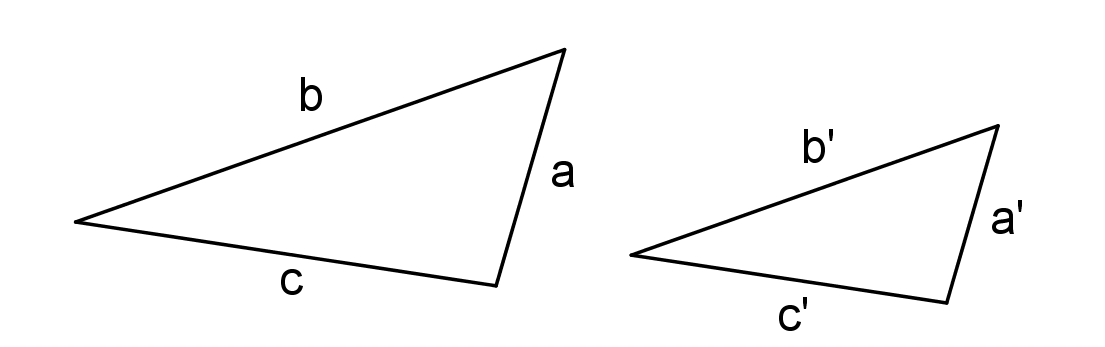
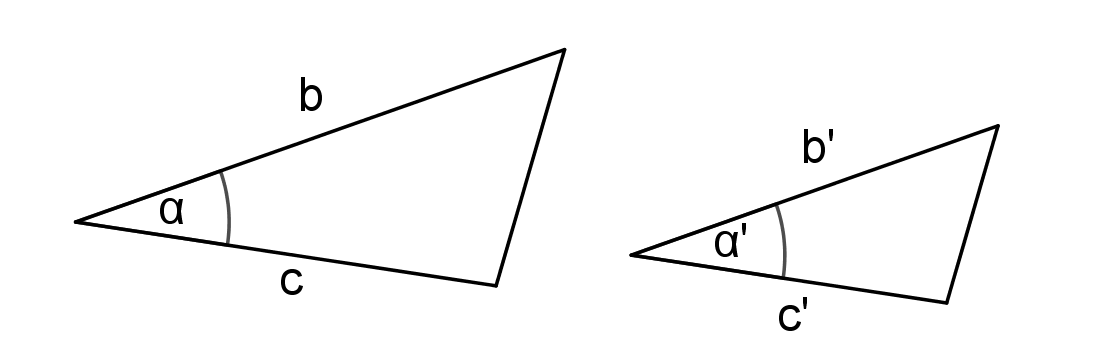
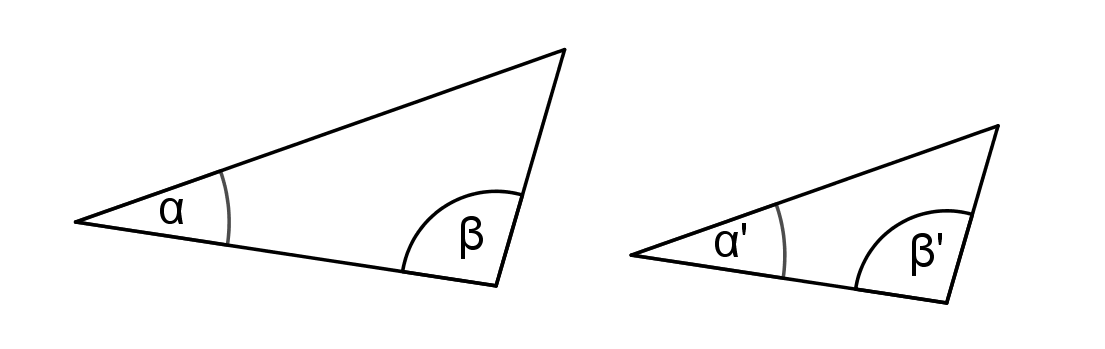
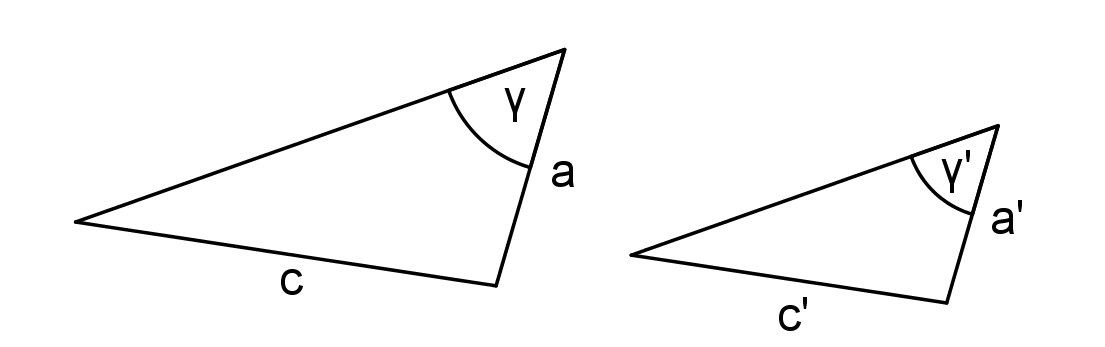
Protože existují dva různé trojúhelníky, které se shodují ve dvou stranách a úhlu proti měnší z nich!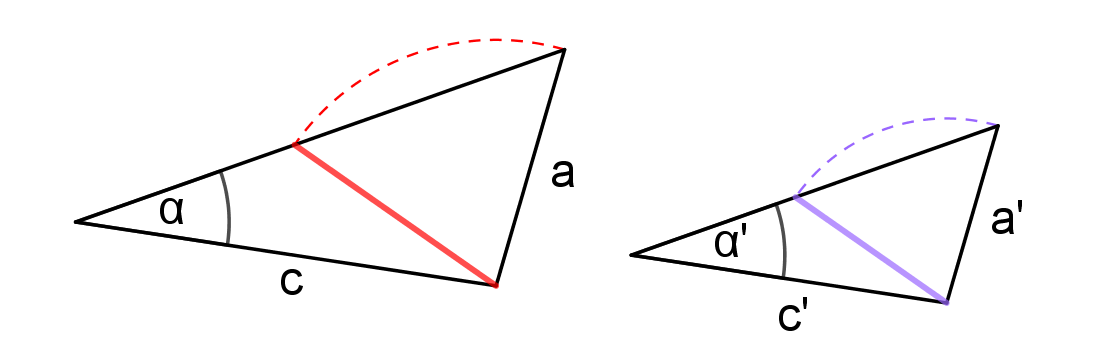
ÚKOL č. 11: Jsou dány tři různé přímky o1, o2, o3 procházející bodem O; na přímce o1 je dán bod A1 různý od O. Sestrojte trojúhelník ABC tak, aby o1, o2, o3 byly osami jeho stran a bod A1 středem strany BC. Proveďte rozbor úlohy náčrtkem a navrhněte postup konstrukce. Vlastní konstrukci proveďte formou online materiálu vytvořeného v GeoGebře, s případnou možností přehrát postup konstrukce krok za krokem.
-
Analytická geometrie.
PŘEDNÁŠKA 12 Stejnolehlost.
Úvod do geometrie (2019), str. 84-87. / Planimetrie (2020)., str. 108-124.
GeoGebra applet: Stejnolehlost
Zobrazení kružnice ve stejnolehlosti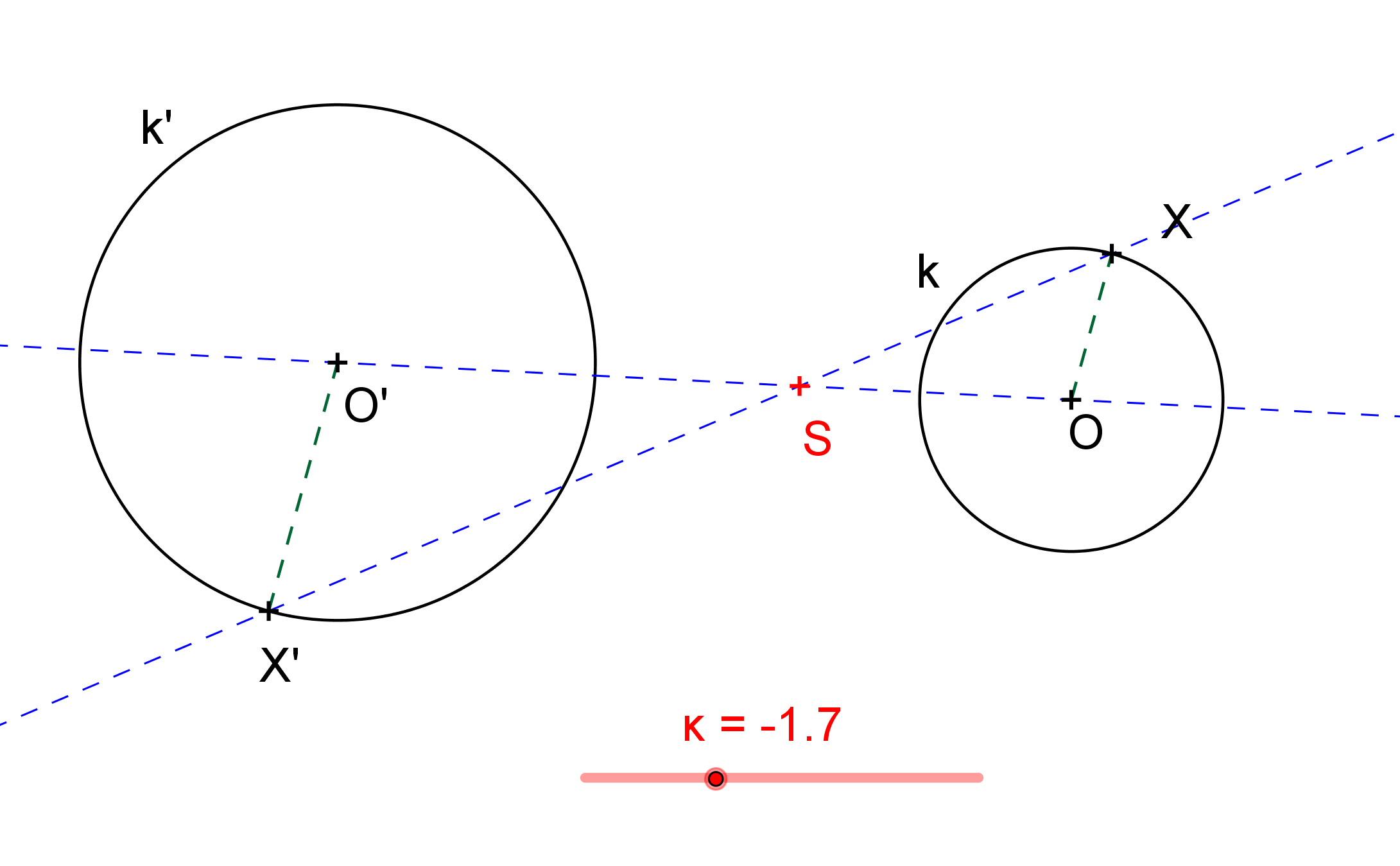
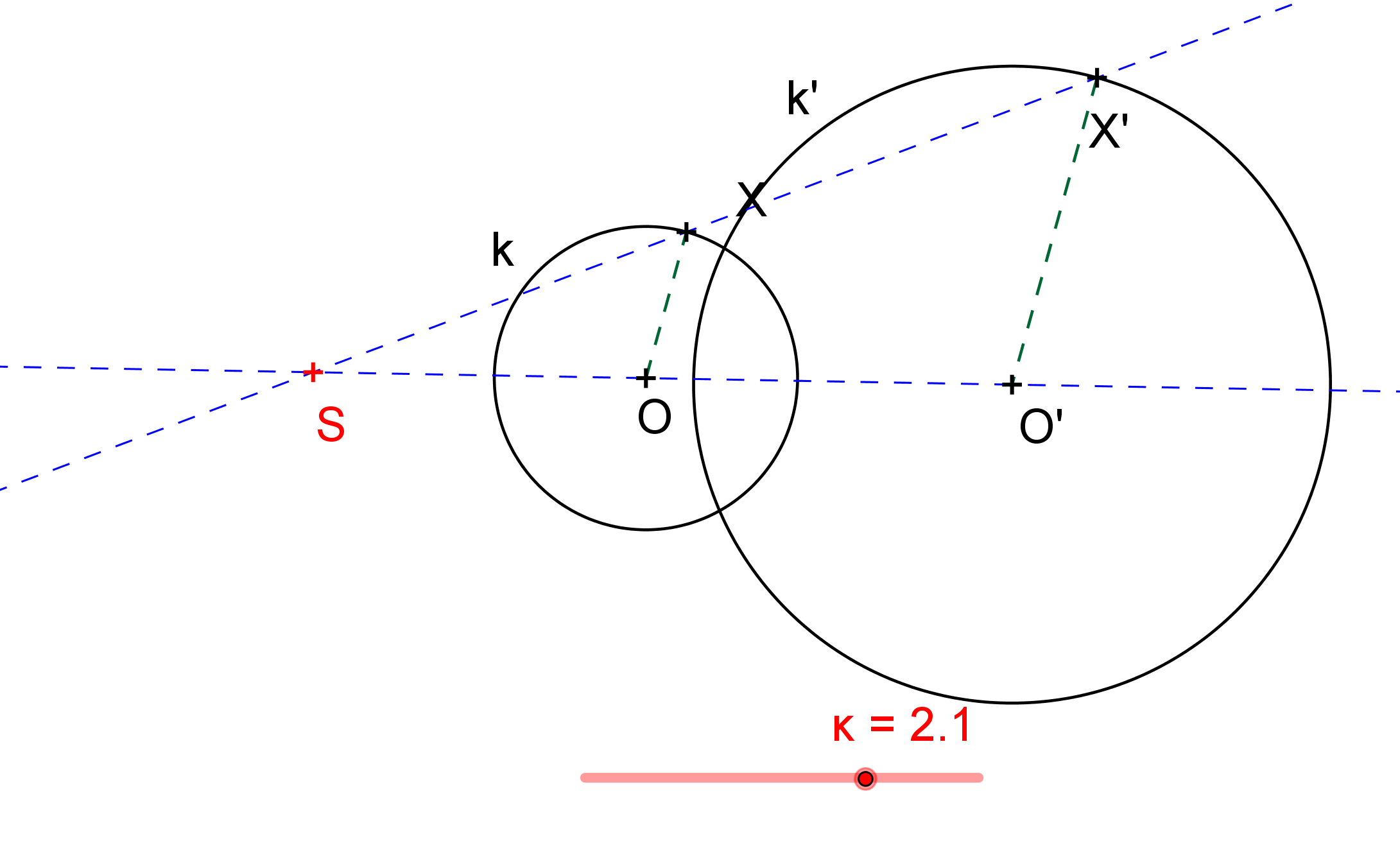
[GeoGebra applet: Zobrazení kružnice ve stejnolehlosti]
Každé dvě kružnice jsou stejnolehlé; existují jedna, většinou však dvě stejnolehlosti, v nichž se jedna zobrazí na druhou. Zajímá nás, jak určíme středy těchto stejnolehlostí. Koeficenty jsou jasné, jejich absolutní hodnota je rovna poměru poloměrů příslušných kružnic, v pořadí obraz - vzor.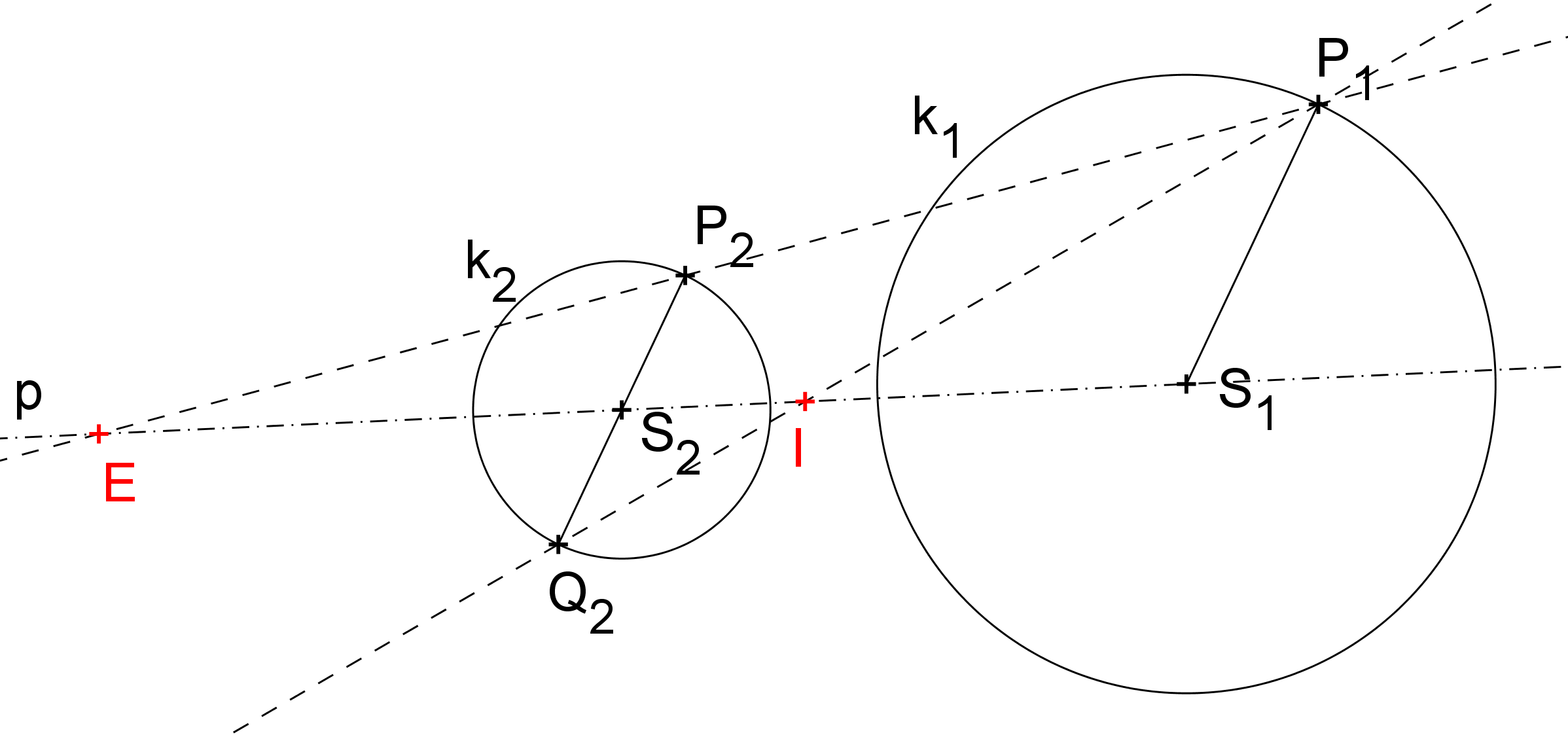
[GeoGebra applet: Určení středů stejnolehlostí dvou kružnic]
Společné tečny kružnic procházejí středy jejich stejnolehlostí, vnější tečny středem E, vnitřní tečny středem I. Stačí tedy najít tyto středy a potom sestrojit tečny z každého z nich k jedné z daných kružnic (užitím Thaletovy kružnice), automaticky budou tečnami i druhé kružnice.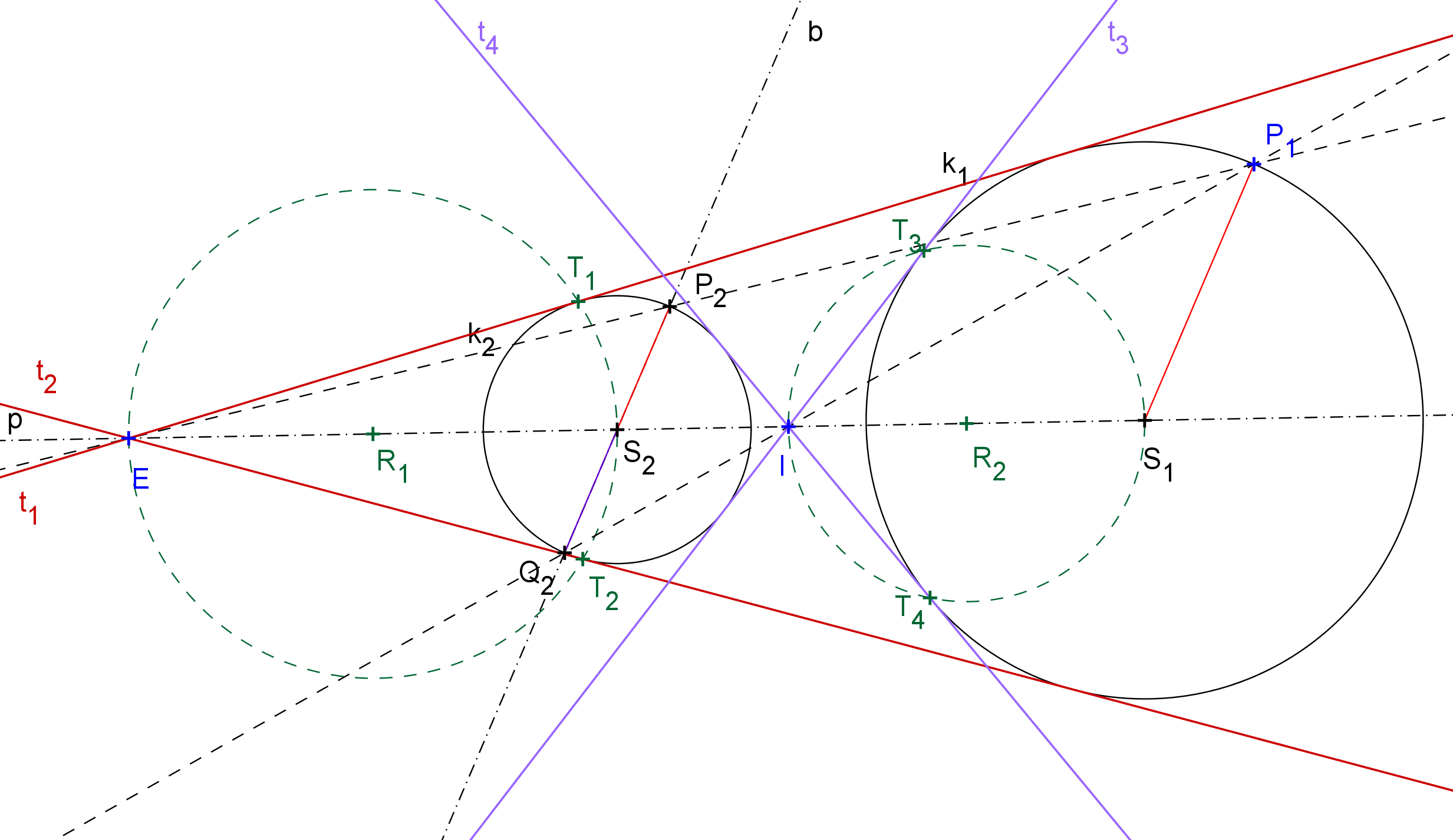
[GeoGebra applet: Konstrukce společných tečen dvou kružnic]
Každá podobnost v rovině se dá rozložit na stejnolehlost a shodnost. Viz Geometrie 2 (2018), str. 102.
Prémiový úkol č. 12: Na obrázku jsou dvě kružnice k a l, ze středu každé z nich jsou sestrojeny tečny k té druhé. Přitom tečny z bodu A protínají kružnici k v bodech P, Q a tečny z bodu B protínají kružnici l v bodech R a S. Dokažte, že |PQ|=|RS|. (GEO2-2020/PU12)
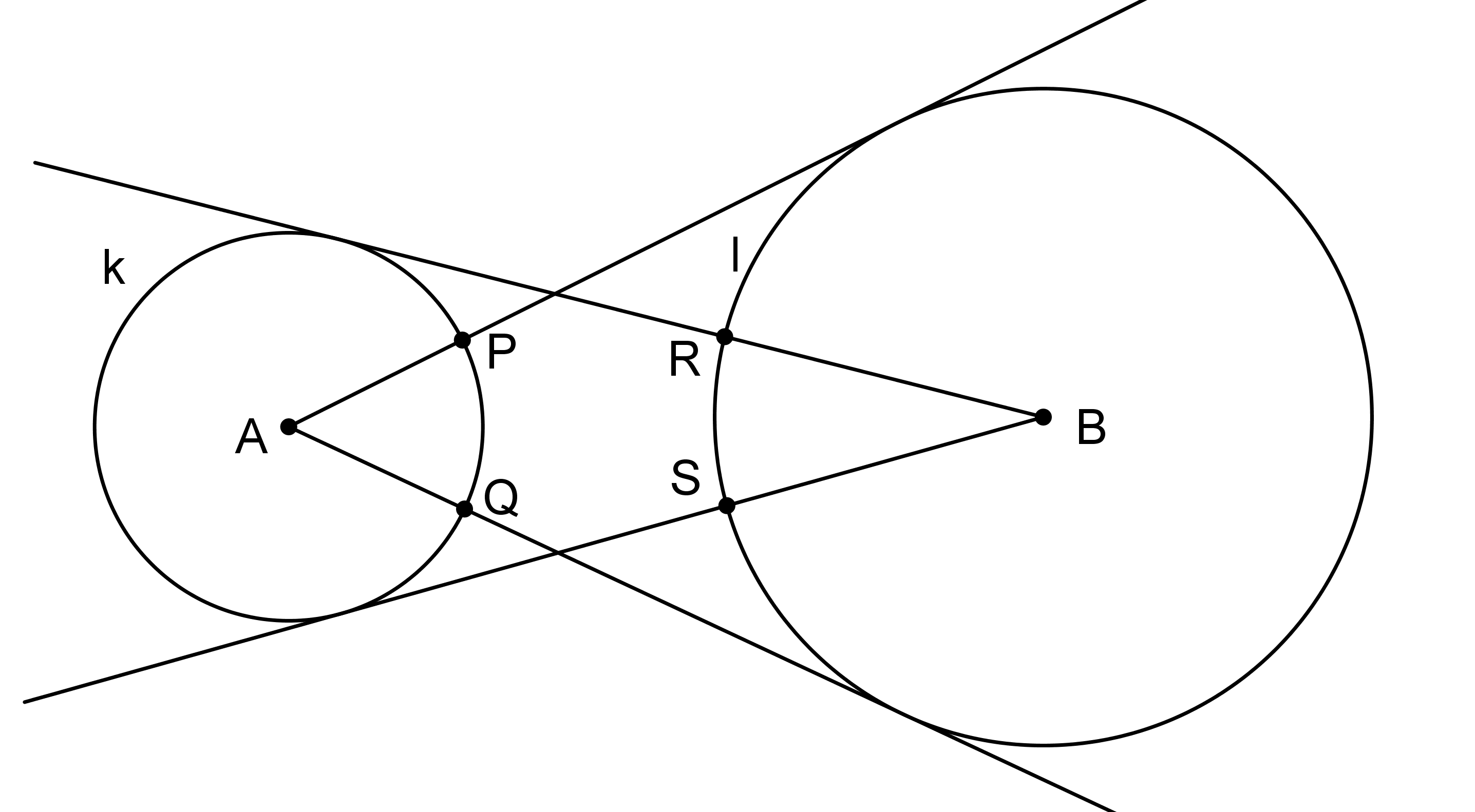
CVIČENÍ 12 Geogebra Classroom
Přihlaste se do GeoGebra Classroom s kódem, který Vám bude sdělen.
Příklad 1: Je dána kružnice k a bod M uvnitř této kružnice. Sestrojte všechny tětivy kružnice k, které jsou bodem M rozděleny na části v poměru 2:3.
Příklad 2: Narýsujte libovolný trojúhelník ABC. Uvnitř strany AC sestrojte bod X a uvnitř strany BC bod Y tak, aby platilo |AX| = |XY| a XY || AB.
ÚKOL č. 12: Do půlkruhu s průměrem AB vepište čtverec KLMN tak, aby strana KL ležela na úsečce AB a další dva vrcholy M, N na dané půlkružnici.
-
Topologie.
PŘEDNÁŠKA 13 Mocnost bodu ke kružnici
Planimetrie (2020), str. 129-136.Rozdělení úsečky v poměru zlatého řezu
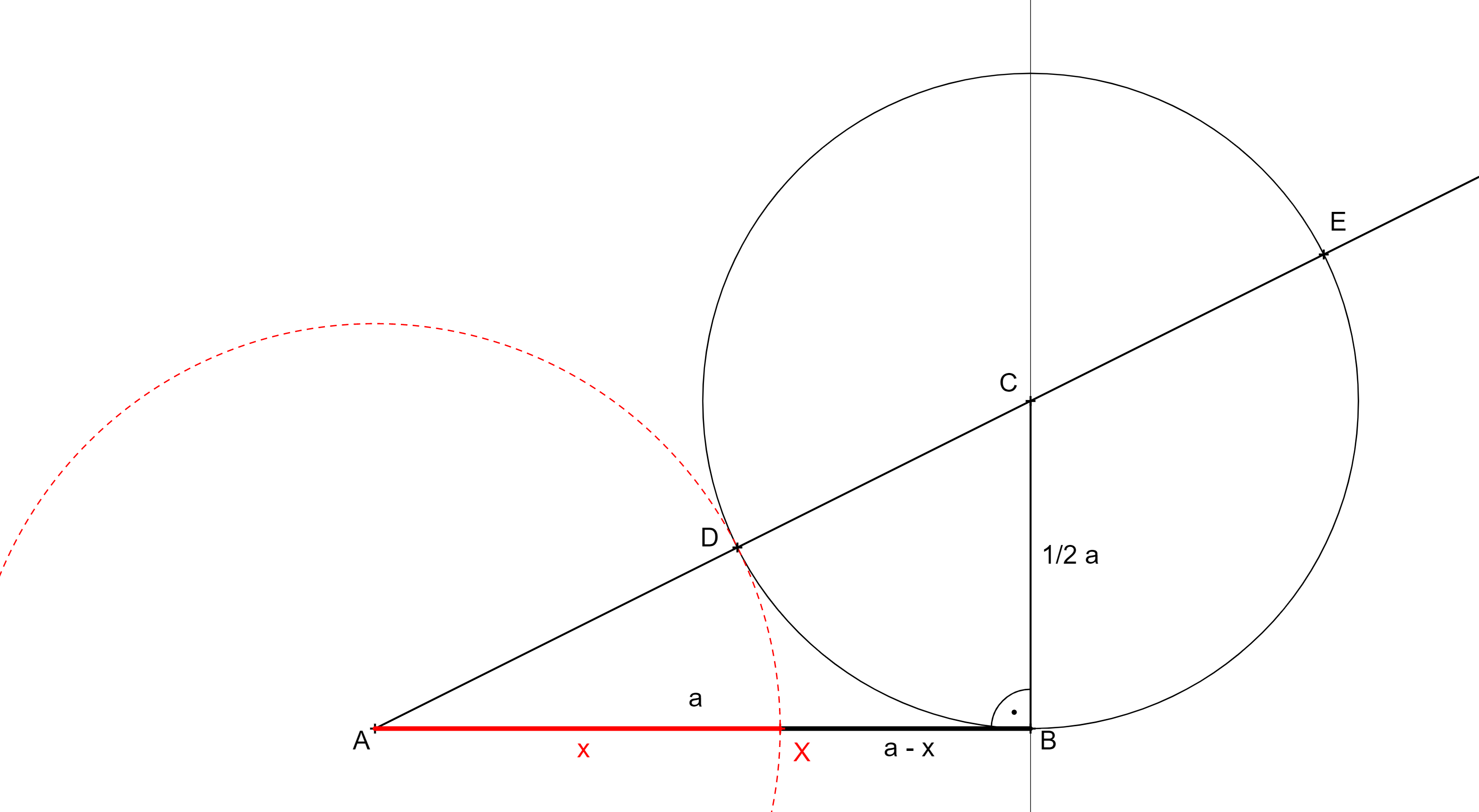
Analytická geometrie.
Úvod do geometrie (2019), str. 44-48. / Planimetrie (2020), str. 7-8. / Lineární algebra a geometrie (2020), str. 131-133.
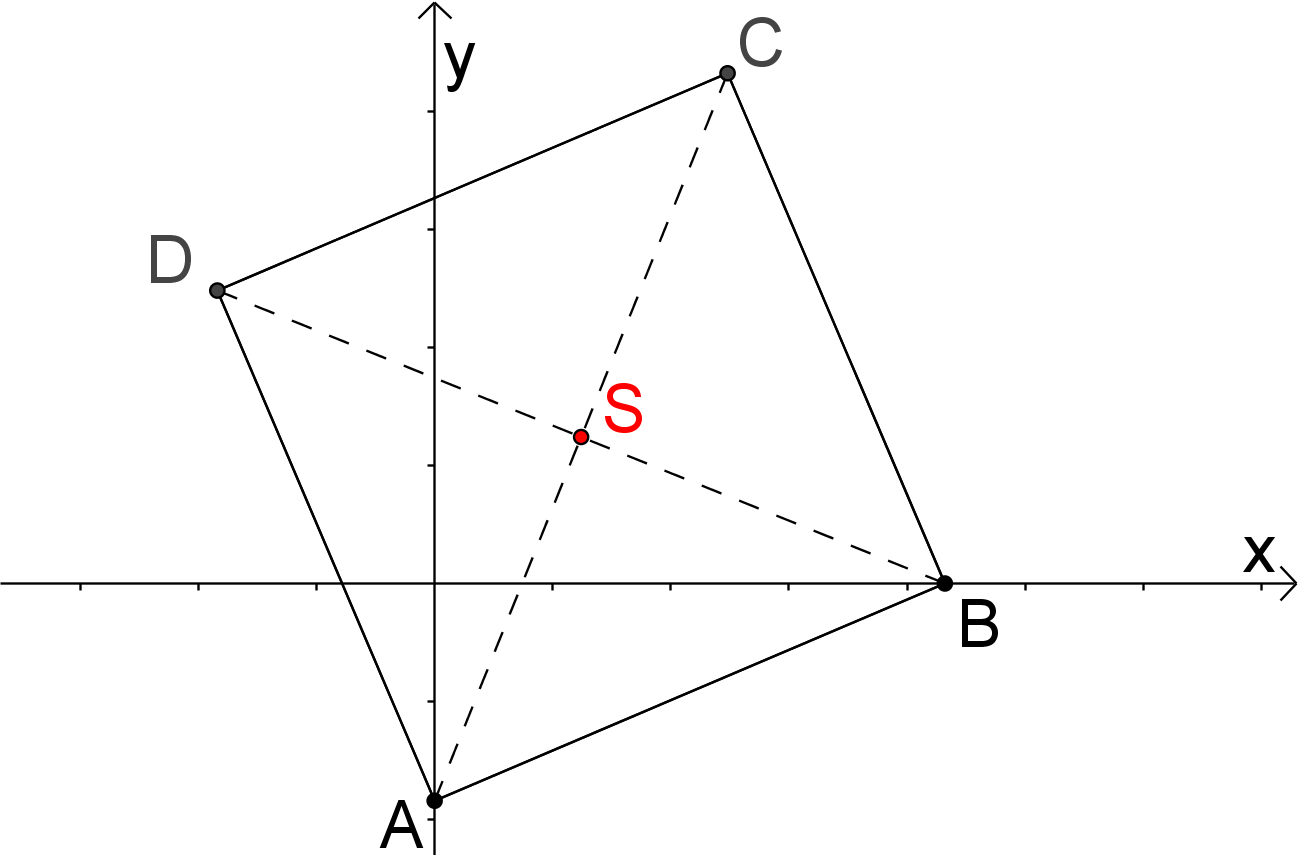
Prémiový úkol č. 13: Pro libovolný čtverec ABCD s vrcholem A na ose y a s k němu sousedním vrcholem B na ose x platí, že souřadnice jeho středu S (viz obrázek) jsou buď čísla shodná nebo opačná. Dokažte! (PLA-2017/PU4)
CVIČENÍ 13 - Souřadnice vektoru, souřadnice bodu, parametrické rovnice přímky a jejích částí, parametrické rovnice roviny a poloroviny, vzdálenost bodů, rovnice kružnice a kulové plochy, odchylka dvou vektorů: 7UM2 Cv Ut 11.05.2021.pdf / 7UM2 Cv Ct 13.05.2021.pdf
- Odchylka dvou přímek: Lineární algebra a geometrie (2020), str. 69-71.
- Vzdálenost dvou bodů, vzdálenost bodu od přímky a od roviny: Lineární algebra a geometrie (2020), str. 169-170.
Příklad 1: V rovině jsou dány dva pevné body A[-1, 0] a B[1, 0]. Určete množinu všech bodů X[x, y] této roviny, pro které platí |AX|/|BX|=k, kde k je reálná konstanta (např. k = 2). [Řešení v GeoGebře]
ÚKOL č. 13: V rovině jsou dány body A[0; 0], B[k; l]. Vyjádřete souřadnice středu S čtverce, jehož vrcholy jsou body A, B, pomocí souřadnic těchto bodů.
-
Aplikace geometrie.
PŘEDNÁŠKA 14 Topologie
Wikipedia: Topology / Wikipedia: Topologie
Topologie je poměrně široká matematická disciplína. My na ní zde nazíráme pouze z perspektivy jejích počátků, kdy se jednalo o disciplínu geometrickou. Potom ji můžeme charakterizovat jeko geometrickou disciplínu, která se zabývá vlastnostmi geometrických objektů (obrazce či tělesa), které zůstanou zachovány i tehdy, když objekt podrobíme deformaci, která mění jeho metrické a projektivní vlastnosti. Viz například transformace hrnečku na torus nebo krávy na kulovou plochu na stránce https://en.wikipedia.org/wiki/Topology, nebo transformace reálného plánu města na mapu dopravního spojení, viz historie vzniku ikonického plánu tras podzemní dráhy v Londýně na stránce https://londonist.com/2016/05/the-history-of-the-tube-map.
Známou úlohou, při jejímž řešení se dá výhodně uplatnit "topologický přístup" (tj. odhlédnutí od metrických vlastností a proporcí zkoumaného útvaru) je problém sedmi mostů města Královce, viz Wikipedia: Sedm mostů města Královce / Wikipedia: Seven Bridges of Königsberg.
Grafická reprezentace problému sedmi mostů nás dovede k pojmu graf a k teorii grafů. Zkoumáme, zda lze daný graf nakreslit jedním tahem (takovému grafu říkáme Eulerovský). Na řešení stejné otázky jsou založené úlohy zvané jednotažky.
ÚKOL: Prostudujte materiály věnované jednotažkám na stránce http://home.pf.jcu.cz/~math4all/aktivity_u_s.php?akt_id=701, Vymyslete vlastní jednotažku!
Příkladem topologické věty (ve smyslu matematické věty) je Eulerova formule (též Eulerův vztah) pro konvexní mnohostěny:
[počet stěn] + [počet vrcholů] - [počet hran] = 2
s + v - h = 2
4 + 4 - 6 = 2 6 + 8 - 12 = 2Euler's Formula (www stránka) / Wikipedia: Euler characteristic / dynamický (topologický) důkaz
Möbiova páska
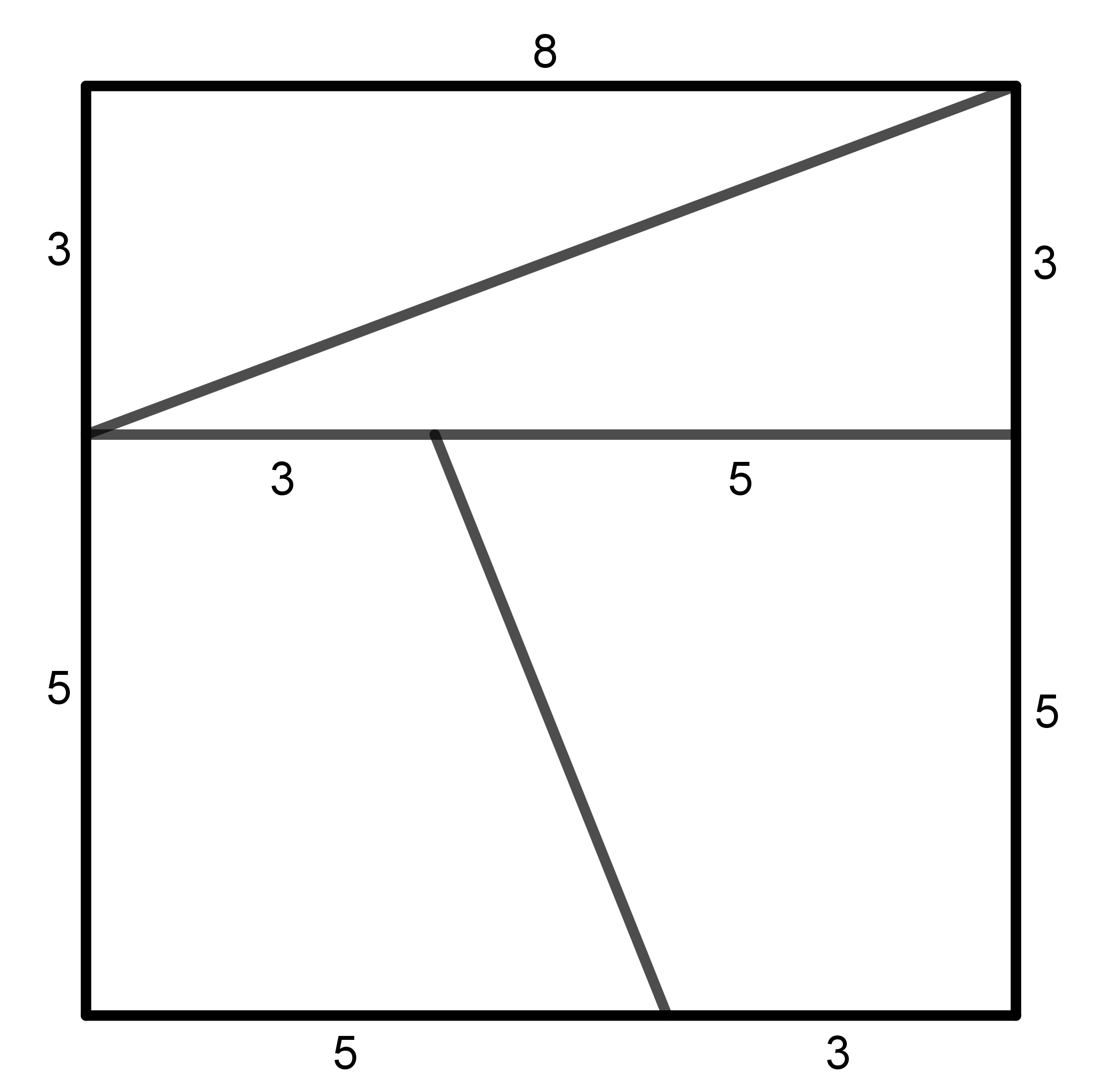
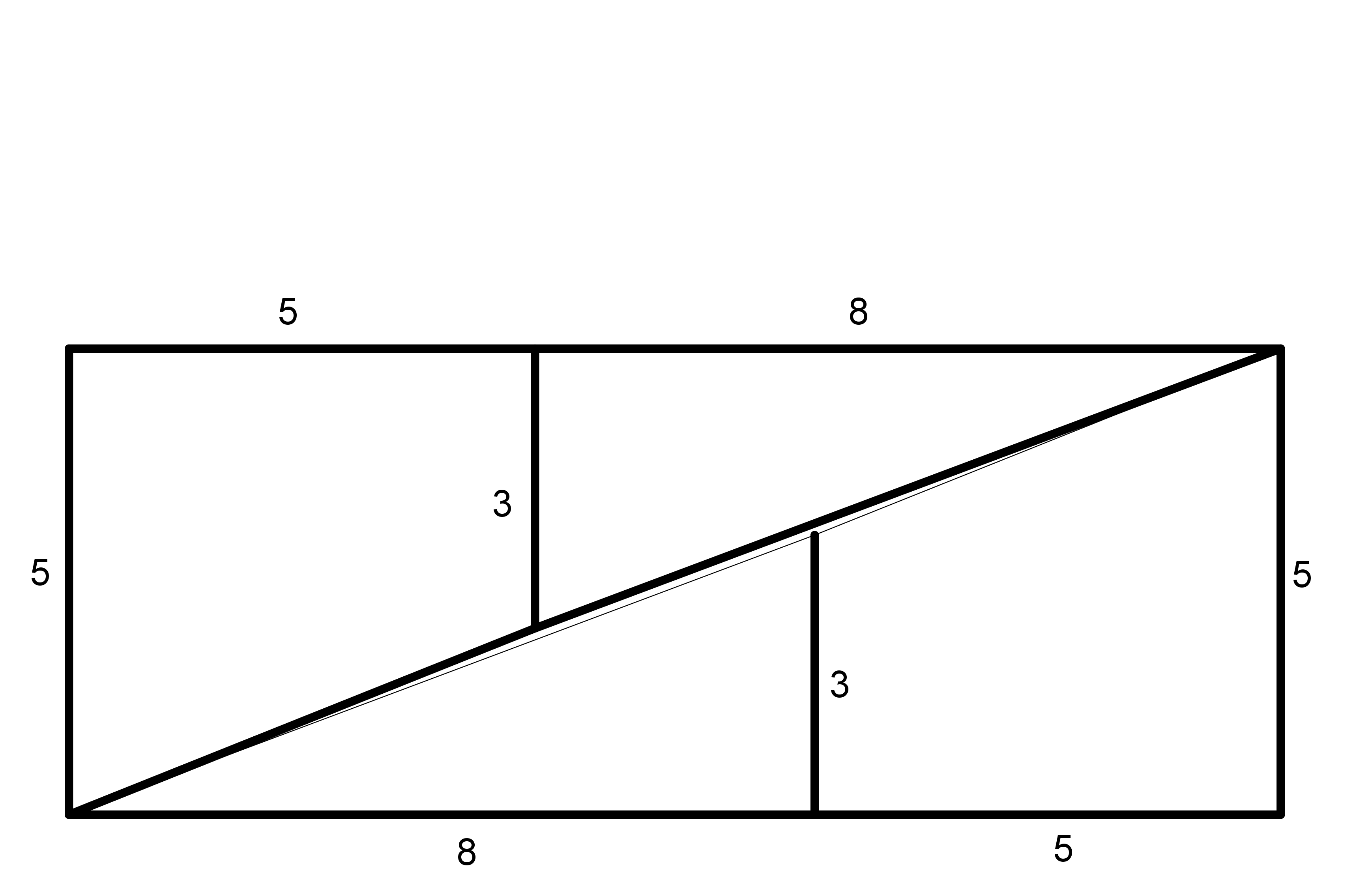
Wikipedia: Möbiova páskaPrémiový úkol č. 14: Podle levého obrázku rozstřiháme čtverec o straně 8 cm na čtyři části, z nichž sestavíme obrazec ve tvaru obdélníku vpravo. Jeho rozměry jsou 13 cm × 5 cm. Porovnáme-li obsahy obou obrazců, čtverce a obdélníku, zjistíme, že se liší o 1 cm2. Čtverec má obsah 64 cm2, obdélník pak 65 cm2. Jak mohl tento rozdíl vzniknout? Vysvětlete! (PLA-2018/PU3)
CVIČENÍ 14 Příklad 1: Dokažte, že výšky v trojúhelníku, uvažované jako přímky, mají jeden společný bod. Tento bod nazýváme "ortocentrum".
Řešení: GeoGebra (18.05.2021)
Literatura
[1] Pomykalová, E., Matematika pro gymnázia - Planimetrie. Prometheus, Praha, 2008.
[2] Kuřina, F.: 10 geometrických transformací. Prometheus, Praha, 2002.
[3] Kuřina, F.: 10 pohledů na geometrii. Akademie věd České republiky, 1996.
[4] Pech, P., Klasické vs. počítačové metody při řešení úloh v geometrii, České Budějovice, PF JU, 2005.
[5] Pech, P., Analytická geometrie lineárních útvarů,
České Budějovice, PF JU, 2004.
[6] Voráčová a kol., Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha, 2012.
[7] Sekanina, M. a kol.: Geometrie I, SPN, Praha 1988.
[8] Sekanina, M. a kol.: Geometrie II, SPN, Praha 1988.
[9] Leischner, P. Geometrická zobrazení, Jihočeská univerzita v Českých Budějovicích, 2010.
[10] Audin, M.: Geometry, Springer, 2003.
[11] Budinský, B.: Analytická a diferenciální geometrie. SNTL, Praha, 1983.
[12] Vyšín, J. . a kol.: Geometrie pro pedagogické fakulty II, Bratislava, 1970.
[13] Eukleides, Eukleidovy základy (Elementa), překlad F. Servít, 1907.
Dostupné na https://commons.wikimedia.org/wiki/File:Eukleides_Servit.pdf
[14] Leydold, J., Petry, M. : Introduction to Maxima for Economics (pdf) [online]
[15] Hašek, R., Noruláková, M.: Program wxMaxima ve výuce matematiky (pdf) [online]. Sborník příspěvků 5. konference Užití počítačů ve výuce matematiky, 2011.
Internetové odkazy
Software ke stažení
www.geogebra.org ... program GeoGebra (zdarma)
wxmaxima-developers.github.io/wxmaxima ... program wxMaxima (zdarma)
Materiály pro výuku a sebevzdělávání
i2geo.net ... portál pro sdílení výukových materiálů dynamické geometrie
wiki.geogebra.org ... GeoGebra Wiki - manuál, výukové materiály, fórum apod.
wiki.geogebra.org/cs/ ... postupně překládaná česká verze GeoGebra Wiki
www.youtube.com/user/GeoGebraChannel ... GeoGebra na YouTube
www.geogebratube.org ... Materiály v GeoGebře ke stáhnutí
www.cut-the-knot.org ... Interactive Mathematics Miscellany and Puzzles
http://www.math.uoc.gr ... Geometrikon - galerie geometrických témat
Požadavky na studenta
- Zkouška
- Zkouška má dvě části, písemnou a ústní, které se vykonávají v jeden den. Začíná se písemnou částí, ústní částí lze pokračovat pouze po úspěšném vypracování písemné části (tj. hodnocení nejhůře 3). Písemná část zkoušky se skládá ze tří příkladů (zdroje příkladů jsou na této stránce vyznačeny červeně), u konstrukčních úloh je kromě rozboru požadován popis konstrukce nebo její provedení, proto je vhodné přinést si rýsovací potřeby. Otázka k ústní části bude losována ze zveřejněných 12 otázek (viz Otázky ke zkoušce KMA/7UM2 2021).
-
Podmínky řešení prémiových příkladů: Srozumitelný a přehledný zápis řešení problému, pochopitelně doplněný alespoň jedním obrázkem,
můžete posílat během 1 týdne následujícího po dni zadání (zadání proběhne vždy na přednášce) na adresu hasek@pf.jcu.cz.
Dokument obsahující řešení může mít libovolnou formu, od oskenování ručně psaného řešení až po text napsaný v textovém editoru.
Vždy se však musí jednat o autentický text vypracovaný tím, kdo dokument posílá. Prvních pět autorů správných řešení bude odměněno zvýhodněním 0.25 klasifikačního stupně
při hodnocení zkouškové písemky.
Poznámka: Pro záznam řešení mobilním telefonem doporučuji použít mobilní aplikaci pro skenování dokumentů, např. Microsoft Lens.
Roman Hašek, katedra matematiky PF JU, kontakt: hasek@pf.jcu.cz