DESKRIPTIVNÍ GEOMETRIE 2 - KMA/DG2 |
Deskriptivní geometrie se věnuje zkoumání geometrických vztahů trojrozměrných objektů
prostřednictvím jejich dvojrozměrného znázornění.
Její studium nám tak zprostředkovává
poznání a pochopení stereometrických vztahů, učí nás, jak správně interpretovat
dvojrozměrné pohledy na tyto vztahy a také významně kultivuje naši schopnost prostorové
vztahy graficky vyjádřit způsobem každému srozumitelným.
Předmět Deskriptivní geometrie 2 se věnuje především zobrazování základních těles (hranol, jehlan, kvádr, válec, kužel a koule) v Mongeově promítání, kosoúhlém promítání a v pravoúhlé axonometrii.
Osnova předmětu
- Osová afinita, afinita mezi kružnicí a elipsou.
PŘEDNÁŠKA 1
Úvod. Představení probíraných zobrazovacích metod. Středová kolineace. Osová afinita.
Princip středového a rovnoběžného promítání (Středové promítání / Rovnoběžné promítání).
Středová kolineace a osová afinita, v prostoru i v rovině (Středová kolineace / Osová afinita).
Příklad: Je dána přímka o a trojúhelník ABC. Sestrojte obraz A'B'C' trojúhelníku ABC v takové osové afinitě, aby byl trojúhelník A'B'C' rovnostranný. [Řešení v programu GeoGebra]
PŘEDNÁŠKA 2
Elipsa jako afinní útvar ke kružnici.
Příklad: Ve volném rovnoběžném promítání zobrazte krychli, která má na stěnách nakresleny kružnice o průměru a (délka hrany krychle). [Krychle s kružnicemi na stěnách.] [Řešení v programu GeoGebra.]
Příklad: Jsou dány sdružené průměry elipsy k. Krajní body jednoho z nich jsou současně krajními body kružnice l. Určete afinitu, v níž kružnici l odpovídá elipsa k. [Znázornění v programu GeoGebra.]
Domácí úkol: Zobrazte danou kružnici v dané osové afinitě tak, že se zvolené sdružené průměry kružnice zobrazí na osy odpovídající elipsy (Řešení v GeoGebře nahrajte na GeoGebraTube a pošlete mi e-mailem příslušnou adresu.).
- Mongeovo promítání, zobrazení kužele.
- Kosoúhlé promítání, zobrazení kužele.
PŘEDNÁŠKA 3
Elipsa jako afinní útvar ke kružnici.
Proužková konstrukce elipsy, Rytzova konstrukce elipsy a jejich souvislost s afinitou elipsy a kružnice.
Zobrazení kružnice ležící v půdorysně (v rovině xy) v Mongeově promítání a v kosoúhlém promítání
Příklad: Zobrazte rotační kužel s podstavou k(S;r); S = [6,5,0], r = 5 cm, ležící v půdorysně a s výškou v = 5 cm:- v Mongeově promítání,
- v kosoúhlém promítání; ω = 135°, q = 1/2.
- Pravoúhlá axonometrie, úlohy polohové a metrické.
PŘEDNÁŠKA 4
Zobrazení kružnice ležící v půdorysně (v rovině xy) v pravoúhlé axonometriiPŘÍKLAD NA ZOPAKOVÁNÍ (Zobrazení bodu v pravoúhlé axonometrii):
V axonometrii, která je zadána axonometrickým trojúhelníkem XYZ o stranách x = 5, y = 4 a z = 5 sestrojte axonometrický průmět bodu A o souřadnicích A[3,5,6] spolu s jeho souřadnicovým kvádrem. [Animace řešení (GeoGebra)]
Příklad: Zobrazte rotační kužel s podstavou k(S;r); S = [6,5,0], r = 5 cm, ležící v půdorysně a s výškou v = 5 cm:
- v pravoúhlé axonometrii [XY = 8, YZ = 10, XZ = 9].
POMOCNÝ PŘÍKLAD ([1], str. 161): K elipse určené ohnisky F1, F2 a hlavními vrcholy A, B veďte bodem R tečny; F1F2 = 5, AB = 8, F1R = 5, F2R = 6.
Při řešení pomocného příkladu využijeme následující vlastnosti elipsy.
V: Tečna elipsy půlí vnější úhly průvodičů bodu dotyku.
V: [Řídicí kružnice elipsy] Množina všech bodů, které jsou souměrně sdružené s jedním ohniskem elipsy podle jejích tečen, je kružnice se středem v druhém ohnisku a s poloměrem rovným délce hlavní osy elipsy.
V: [Vrcholová kružnice elipsy] Množina všech pat kolmic, které jsou spuštěny z ohnisek elipsy na její tečny, je kružnice opsaná okolo středu elipsy s poloměrem rovným délce její hlavní poloosy. - Mongeovo promítání, zobrazování válce, kužele a koule z daných podmínek.
- Kosoúhlé promítání, polohové úlohy, zobrazování základních těles a kulové plochy.
- v pravoúhlé axonometrii [XY = 8, YZ = 10, XZ = 9].
- v Mongeově promítání,
- v kosoúhlém promítání; ω = 120°, q = 3/4.
- v pravoúhlé axonometrii [∠xz = 105°, ∠xy = 135°, XY ≈ 10].
- v Mongeově promítání,
- v kosoúhlém promítání; ω = 120°, q = 3/4.
- v pravoúhlé axonometrii [∠xz = 105°, ∠xy = 135°, XY ≈ 10].
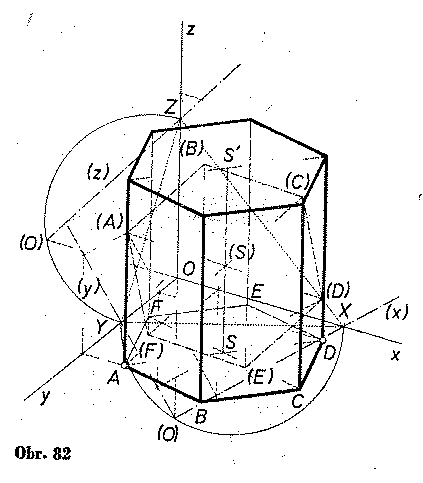
Axonometrický průmět šestibokého hranolu - v Mongeově promítání,
- v kosoúhlém promítání; ω = 120°, q = 3/4.
- v pravoúhlé axonometrii [XY = 9, YZ = 10, XZ = 11].
- jeho stranu a,
- kružnici jemu opsanou o poloměru r.
- Rovinné řezy těles v probraných zobrazovacích metodách.
PŘEDNÁŠKA 7-8
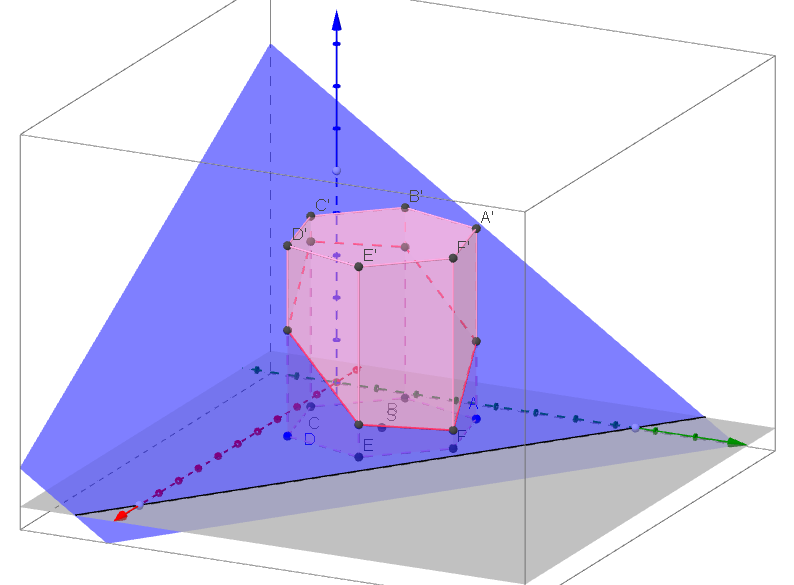
Řez pravidelného n-bokého hranolu rovinou.Příklad: (Pokračování z minulé přednášky) Sestrojte řez pravidelného šestibokého hranolu o výšce v = 9, jehož podstava ABCDEF leží v π; A[2; 8; 0], D[8;1,5;0], rovinou ρ=(20,15,10):
PŘEDNÁŠKA 9
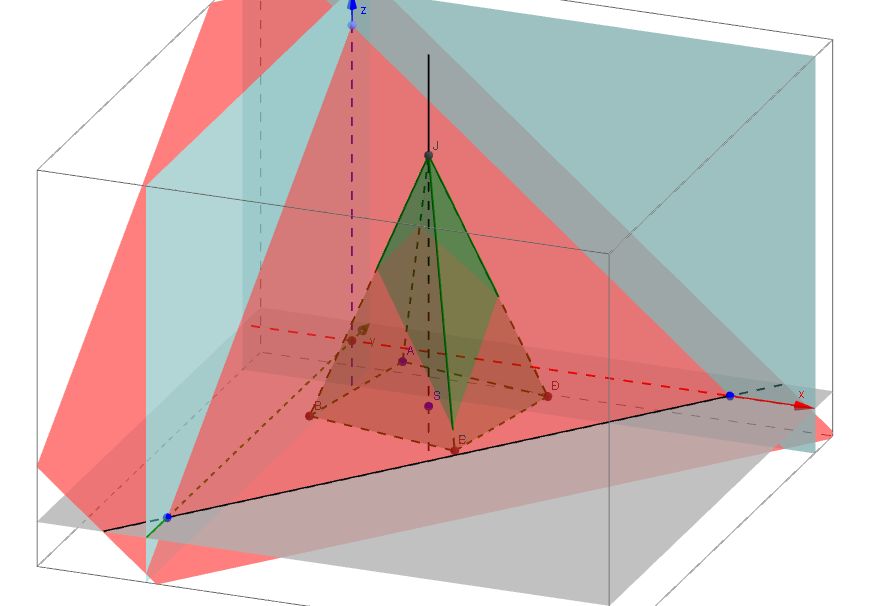
Řez pravidelného n-bokého jehlanu rovinou.Příklad: Sestrojte řez pravidelného čtyřbokého jehlanu o výšce v = 8, jehož podstava ABCD leží v půdorysně π; A[2; 1; 0], S[4; 4;0], rovinou σ=(12,15,10):
PŘEDNÁŠKA 11
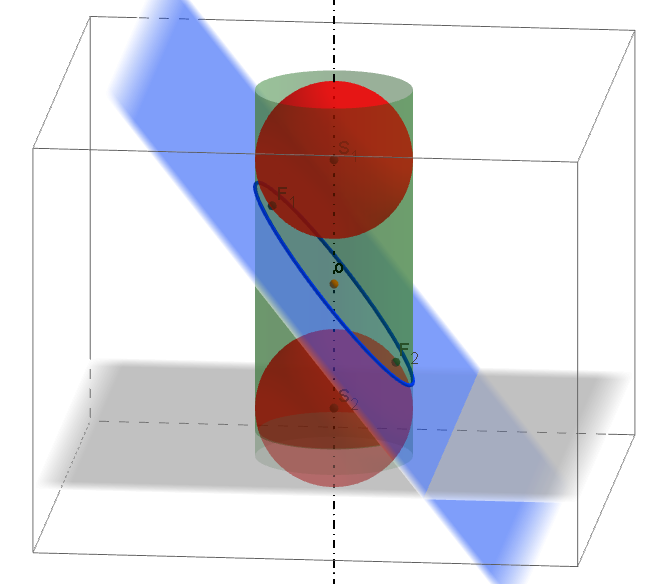
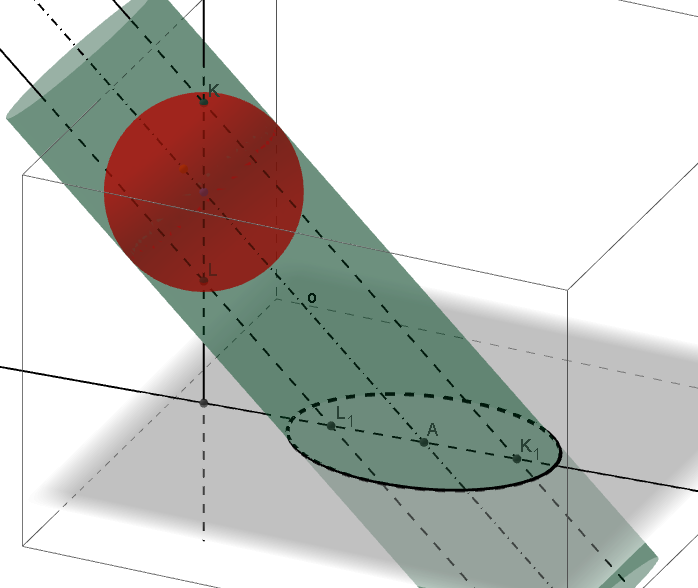
Řez válcové a kuželové plochy rovinou. Zobrazení sféry.Příklad: V pravoúhlé axonometrii [XY = 10, YZ = 11, XZ = 12] zobrazte řez rotačního válce s podstavou v rovině π; [S[4; 4; 0], r = 3,5, v = 9] rovinou σ=(9; ∞; 8).
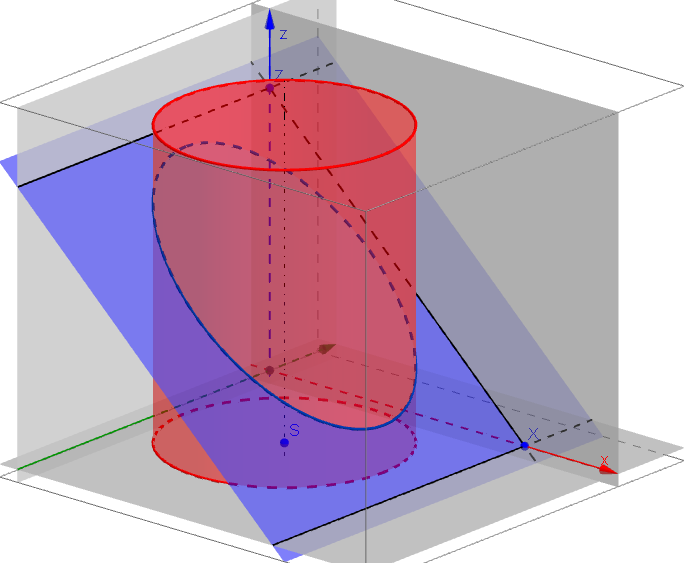
Řez válce rovinouPříklad: V pravoúhlé axonometrii [XY = 10, YZ = 11, XZ = 12] zobrazte řez kužele s podstavou v rovině π; [S[4,5; 4,5; 0], r = 4, v = 10] rovinou σ=(9; ∞; 8).
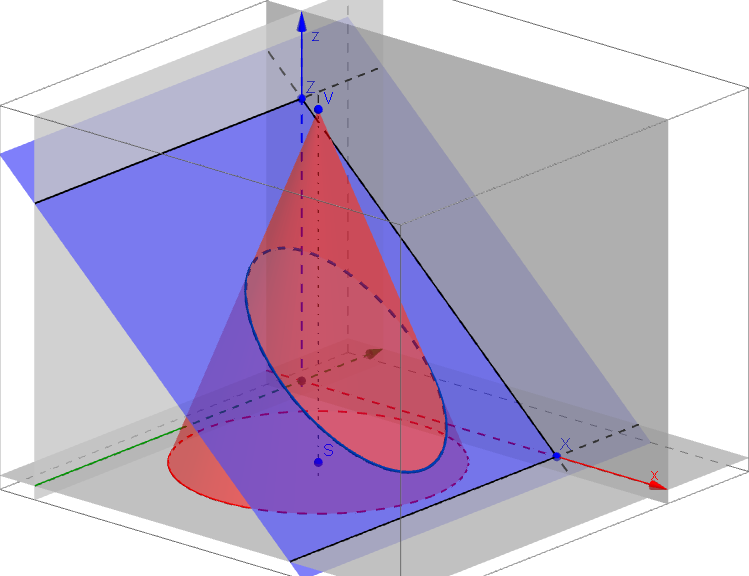
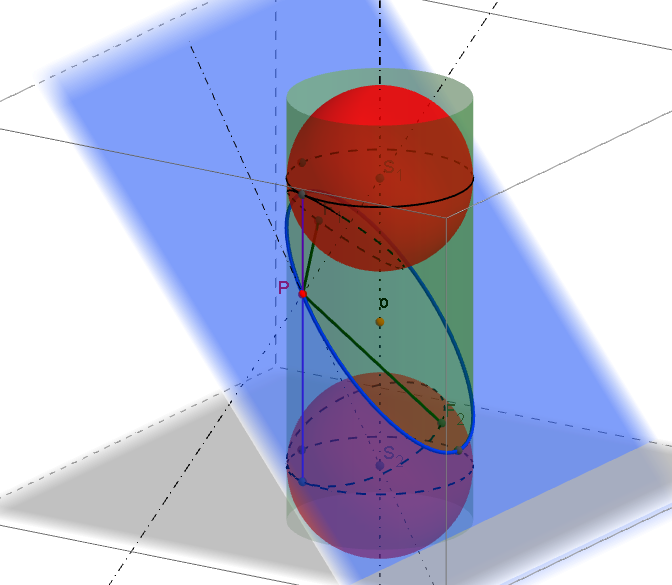
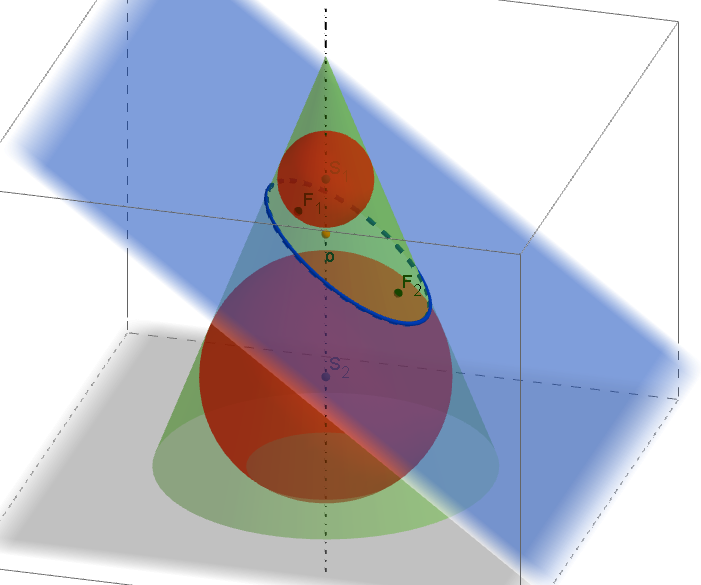
Řez kužele rovinouPříklad: V kosoúhlém promítání (ω = 135°, q = 3/4) zobrazte kulovou plochu o poloměru r = 4 se středem v počátku soustavy souřadnic. Na kulové ploše zobrazte řezy souřadnicovými rovinami π=(xy), ν=(xz), μ=(yz).
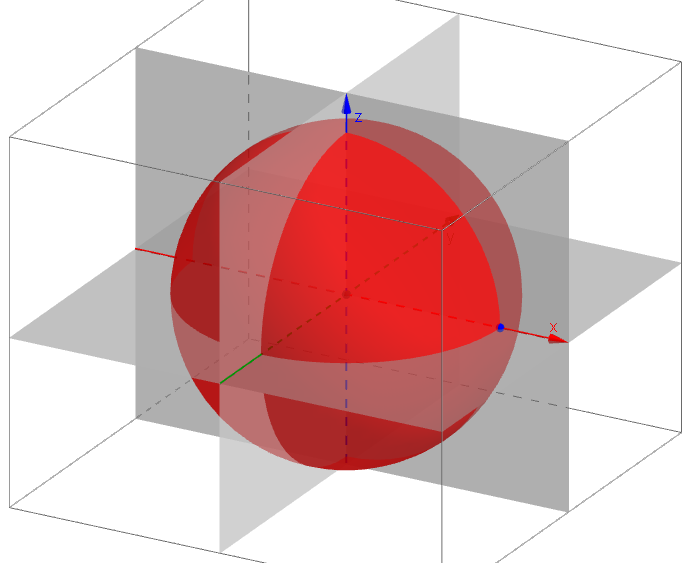
Kulová plochaŘešení:
Kosoúhlým průmětem kulové plochy (sféry) je elipsa (viz obrázek). Jejími ohnisky jsou (dle Quételetovy-Dandelinovy věty pro válcovou plochu) průměty krajních bodů průměru sféry, který je kolmý k průmětně. V případě našeho příkladu leží tento průměr s krajními body E, F v ose y.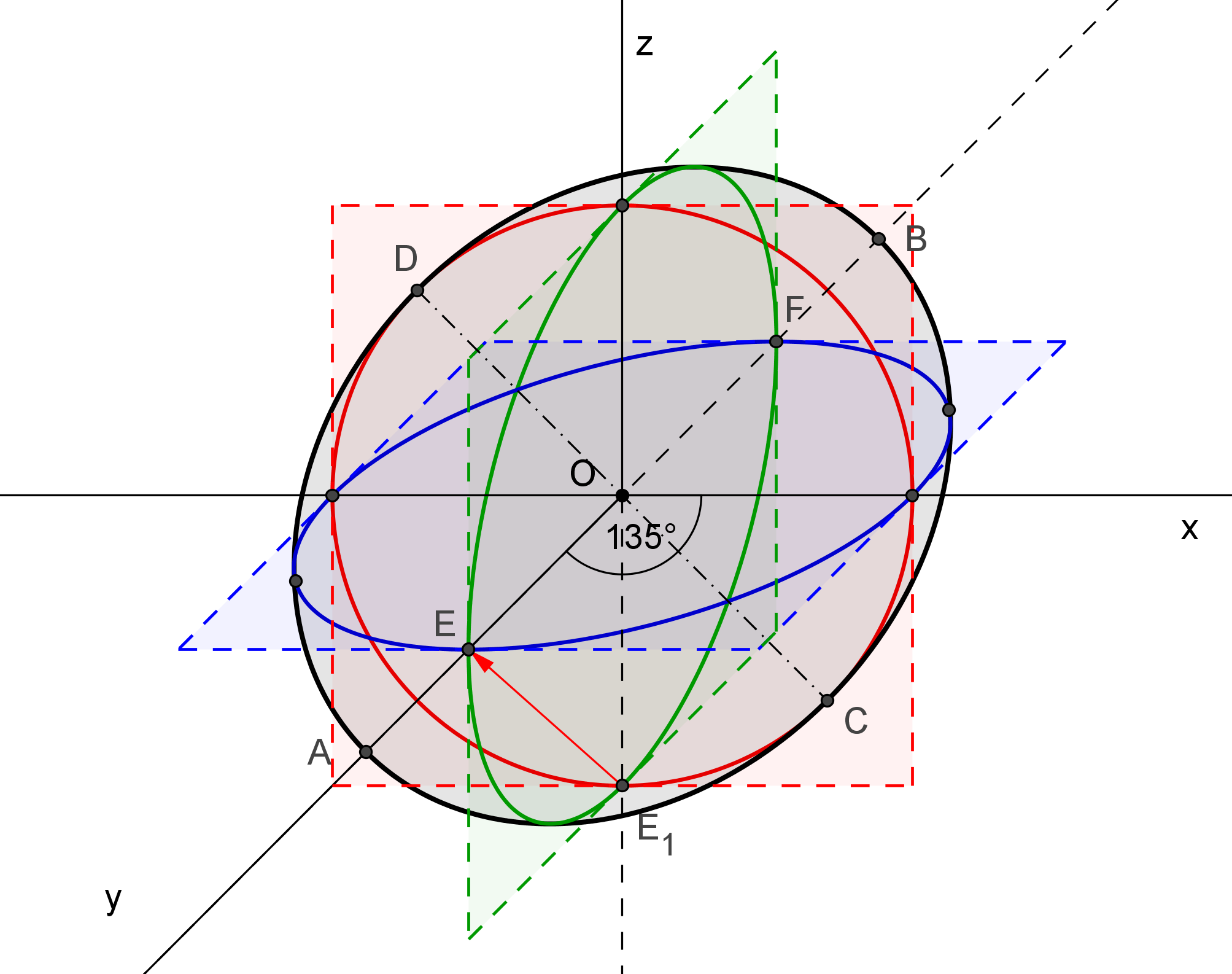
Kulová plocha v kosoúhlém promítání
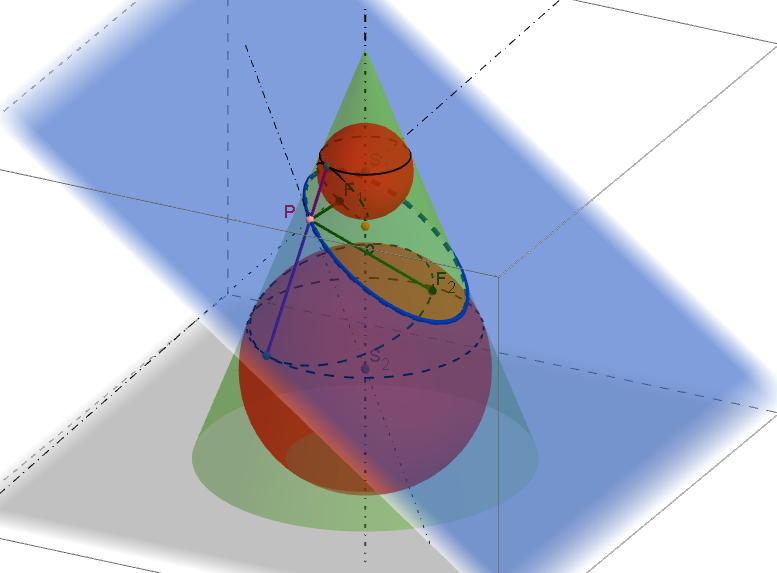
Postup řešení:
1) Hlavní osa elipsy (která je kosoúhlým průmětem dané sféry) leží v ose y. Ohnisky elipsy jsou potom body E, F na ose y, pro které platí: |EO|=|FO|=qr (O je počátek soustavy souřadnic).
2) Vedlejší osa elipsy (která je kosoúhlým průmětem dané sféry) je kolmá k hlavní ose v bodě O. Vedlejšími vrcholy elipsy jsou potom body C, D na této kolmici, pro které platí: |CO|=|DO|=r.
3) Hlavní vrcholy A, B určíme užitím charakteristického trojúhelníku elipsy (a2 = b2 + e2). - Shrnutí.
| PŘEDNÁŠKA 5
Zobrazení kružnice ležící v půdorysně (v rovině xy) v pravoúhlé axonometrii Příklad: (Dokončení z minulé přednášky) Zobrazte rotační kužel s podstavou k(S;r); S = [6,5,0], r = 5 cm, ležící v půdorysně a s výškou v = 5 cm: POMOCNÝ PŘÍKLAD: Elipsa f je dána hlavními vrcholy A, B a jedním bodem M. Určete její vedlejší vrcholy C, D a ohniska F1, F2. Zobrazení hranolu s podstavou v půdorysně (v rovině xy) v Mongeově promítání, kosoúhlém promítání a v pravoúhlé axonometrii
Příklad: Sestrojte průmět (sdružené průměty) pravidelného šestibokého
hranolu o výšce v = 9, jehož podstava ABCDEF leží v π; |
| PŘEDNÁŠKA 6
Konstrukce pravidelného n-bokého hranolu.
Příklad: (Dokončení z minulé přednášky) Sestrojte průmět (sdružené průměty) pravidelného šestibokého
hranolu o výšce v = 9, jehož podstava ABCDEF leží v π; DOMÁCÍ ÚKOL: Sestrojte průmět (sdružené průměty) pravidelného pětibokého hranolu hranolu o výšce v = 8, jehož podstava ABCDEF leží v π; A[10; 10; 0], S[6;6;0]: POMOCNÝ PŘÍKLAD (Konstrukce pravidelného pětiúhelníku.): Sestrojte pravidelný pětiúhelník, znáte-li |
Literatura
[1] Drábek, K., Harant, F., Setzer, O.:. Deskriptivní geometrie I, SNTL, Praha 1978.
[2] Kargerová, M., Deskriptivní geometrie- pro technické školy vysoké, vyšší a střední. Montanex, Praha, 2007.
[3] Pomykalová, E., Deskriptivní geometrie pro střední školy. Prometheus, Praha, 2010.
[4] Urban, A.:. Deskriptivní geometrie I, SNTL, Praha 1982.
[5] Doležal, J.:. Základy geometrie a Geometrie, VŠB-TU Ostrava, on-line učebnice
[http://mdg.vsb.cz/jdolezal/StudOpory/Uvod.html].
[6] Pomykalová, E., Matematika pro gymnázia - Stereometrie. Prometheus, Praha, 1995.
[7] Voráčová a kol., Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha, 2012.
[8] Vrba, A.: Cabri 3D v2 Příručka pro uživatele.
Online: http://www.pf.jcu.cz/cabri/cabri3d/download/Cabri_3D_prirucka.pdf
[9] Harant, M., Lanta, O.: Deskriptivní geometrie pro II. a III. ročník SVVŠ, SPN, 1965.
Internetové odkazy
Software ke stažení
sketchup.google.com ... aplikace Google SketchUp (možnost bezplatného stažení)
www.geogebra.org ... program GeoGebra (možnost bezplatného stažení)
www.rhino3d.com ... 3D modelovací program Rhinoceros
Dalest Elica ... podpora výuky stereometrie
dg.vidivici.cz ... Program Deskriptivní geometrie
Materiály pro výuku a sebevzdělávání
i2geo.net ... portál pro sdílení výukových materiálů dynamické geometrie
wiki.geogebra.org ... GeoGebra Wiki - manuál, výukové materiály, fórum apod.
wiki.geogebra.org/cs/ ... postupně překládaná česká verze GeoGebra Wiki
www.youtube.com/user/GeoGebraChannel ... GeoGebra na YouTube
www.geogebratube.org ... Materiály v GeoGebře ke stáhnutí
http://www.korthalsaltes.com ... Paper models of polyhedra
http://sliceforms.wordpress.com/ ... Sliceforms
Požadavky na studenta
- Seminární práce.
- Řešení domácích prací, které budou zadány v průběhu semestru (dvě tělesa, např.
hranol a válec, vždy v Mongeově promítání, kosoúhlém promítání a v pravoúhlé axonometrii;
vybrané rysy je možno po dohodě s vyučujícím rýsovat pomocí vhodného software).
- Řešení domácích prací, které budou zadány v průběhu semestru (dvě tělesa, např.
hranol a válec, vždy v Mongeově promítání, kosoúhlém promítání a v pravoúhlé axonometrii;
vybrané rysy je možno po dohodě s vyučujícím rýsovat pomocí vhodného software).
- Zkouška.
- Ústní zkouška (jejíž součástí je však i konstrukce či načrtnutí řešení úloh, které se týkají tématu otázky) v rozsahu probíraného učiva.
OTÁZKY KE ZKOUŠCE - DG2 - 2014
- Ústní zkouška (jejíž součástí je však i konstrukce či načrtnutí řešení úloh, které se týkají tématu otázky) v rozsahu probíraného učiva.
Roman Hašek, katedra matematiky PF JU, kontakt: hasek@pf.jcu.cz