DVPP: Geometrie 3 - KMA/3G3Z

Studijní text (pracovní verze): Geometrie III

Osnova předmětu

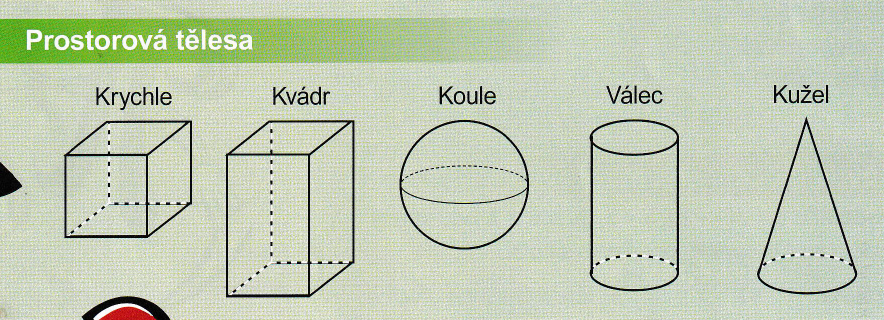
• Základní geometrická tělesa. Stavby z krychlí. Stereometrie.

LN: Matematika pro páťáky Krychle – kvádr – hranol  /  Hranolová plocha – hranol  /  Mnohostěny (prezentace) Euler's Formula (www stránka)  /  Wikipedia: Euler characteristic  /  dynamický (topologický) důkaz Platónská tělesa: Wikipedia: Platonic solid. Stavba z krychlí (str. 94) Matika.in: Stavby z kostek Testy prostorových schopností (orientace v prostoru, tvorba prostorových představ a manipulace s nimi) Santa Barbara Solids Test (https://www.silc.northwestern.edu/santa-barbara-solids-test-inferring-cross-sections-of-3d-objects-2/) Purdue Visualization of Rotations Test (https://usu.instructure.com/courses/387855/quizzes/528051) Spatial Reasoning Test (https://www.assessment-training.com/spatial-reasoning) Optické iluze https://interestingengineering.com/this-cube-is-not-moving-optical-illusions-that-bend-your-brain? https://www.idnes.cz/technet/veda/opticke-iluze-illusion-of-the-year-video.A160712_132525_veda_pka https://www.idnes.cz/technet/veda/opticka-iluze-kognitivni-zkresleni-shepardovy-stoly-shepards-tables.A170426_134159_veda_pka Příklad z didaktického testu jednotné přijímací zkoušky https://prijimacky.cermat.cz/files/files/dokumenty/testova-zadani/4lete-mat/2020/MA_2020_9_A_DT.pdf

• Zobrazení trojrozměrného útvaru v rovině. Promítání. Rovnoběžné a středové promítání.

Rovnoběžné promítání. Středové promítání Volné rovnoběžné promítání a další zobrazovací metody ve stereometrii. (převzato z textu R. Hašek: Základy geometrie) Úvod do deskriptivní geometrie (prezentace). Vybrané metody promítání. Úkol: V kosoúhlém promítání, které je dáno úhlem zkosení ω = 145° a poměrem zkreslení q=1/2, zobrazte kosoúhlý průmět bodu A o souřadnicích A[3,5,6] spolu s jeho souřadnicovým kvádrem. [Animace řešení]

• Volné rovnoběžné promítání. Kolmé promítání. Tři základní průměty. Sdružené průměty trojrozměrného útvaru. Použití v 3D programu.

Úkol:  V programu GeoGebra zobrazte kulovou plochu. Použijte různé druhy promítání. Porovnejte výsledky pravoúhlého a kosoúhlého promítání. 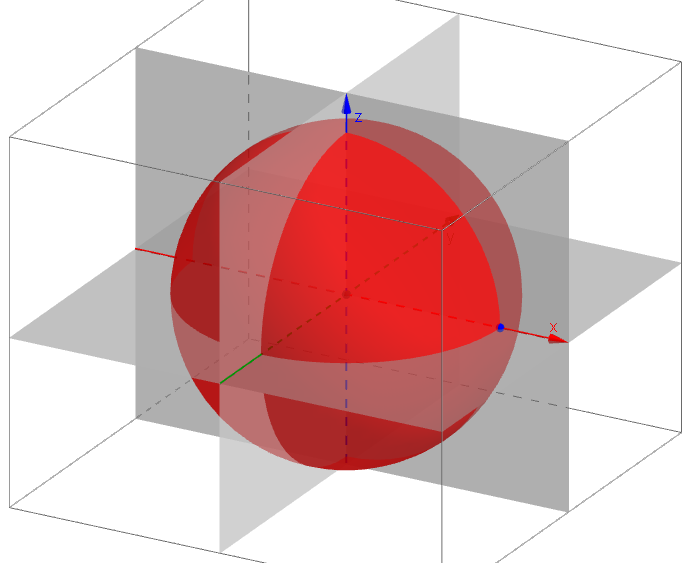Kulová plocha v kosoúhlém promítání

• Rekonstrukce prostorového objektu ze základních průmětů.

nárys - půdorys - bokorys Úkol:  Načrtněte nárys, půdorys a bokorys pro každou z níže zobrazených staveb z krychlí! Poté rozhodněte, zda je správné tvrzení, že těmito sdruženými průměty je libovolná stavba z krychlí dána jednoznačně.

• Eukleidovský trojrozměrný prostor. Souřadnice bodu.

Úkol:  Určete délku úsečky AB; A[-4;2;5], B[2;-2;1]. https://www.geogebra.org/m/pdrfujhv

• Kótované promítání.

Kótované promítání: Zobrazení bodu, přímky a úsečky. Úkol 1:  Určete délku úsečky AB; A[-4;2;5], B[2;-2;1]. [3D znázornění (GeoGebra), Animace řešení, varianta 1, Animace řešení, varianta 2] Úkol 2 (domácí): V kótovaném promítání jsou dány průměty bodů A, B; |A1B1| = 7 cm, zA=5, zB=2. Určete: a) Stopník přímky AB. b) Odchylku α přímky AB od průmětny. c) Skutečnou velikost úsečky AB. d) Vystupňujte přímku AB. [Zadání v PDF] Úkol 3: Určete stopu a hlavní přímky roviny ρ=ABC; A=[2,5;3,5;1,5], B=[7;2,5;0,8], C=[5;6,5;4]. Sestrojte odchylku roviny ρ od průmětny.

• Mongeovo promítání.

Úvod do Mongeova promítání - zobrazení bodu, přímky a roviny. Úkol 1: Sestrojte stopy roviny dané (i) třemi body, (ii) dvěma rovnoběžkami. [Zadání v pdf] Úkol 2: Sestrojte sdružené průměty hlavních přímek h, f roviny σ, která je dána dvěma rovnoběžkami a, b. Zobrazte stopy roviny σ. [Animace] Úkol 3: Sestrojte stopy roviny σ dané různoběžkami a, b.  [Animace (stopníky)] [Animace (hlavní přmky)] Úkol 4: Určete sdružené průměty přímky AB, která leží v rovině ρ(-5; 5; 4); A = [0; 2; ?], B = [2; 1; ?]. [Animace, 3D znázornění: Přímka v rovině (GeoGebra 3D)] Úkol 5: Určete průsečík přímky AB s rovinou ν(-4; 4; 5), A = [2; 1; 0], B = [-5; 4; 8].   [Animace] Úkol 6: Bodem K = [2; 3; 4] veďte přímku kolmou k rovině ρ(-3; 4; 4). Úkol 7: Určete odchylku roviny ρ(-3; 4; 4) od půdorysny π.   [Animace] Úkol 8: Určete skutečnou velikost úsečky AB; A = [3; -1; 2], B = [0; 3; 3,5].   [Animace] Úkol 9: Určete vzdálenost bodu V=[5; 7; 7] od roviny ρ = (5; 4; 6). [Animace - sklopením]   [Animace - otočením] Úkol 10: Sestrojte v Mongeově promítání sdružené průměty kružnice k, která leží v rovině kolmé na nákresnu. [Animace] Úkol 11: Sestrojte v Mongeově promítání sdružené průměty kružnice k, která leží v obecně umístěné rovině. [Animace]

• Kosoúhlé promítání. Axonometrie.

Vybrané metody promítání. Úkol 1: V axonometrii, která je zadána axonometrickým trojúhelníkem XYZ o stranách x=5, y=4 a z=5 sestrojte axonometrický průmět bodu A o souřadnicích A[3,5,6] spolu s jeho souřadnicovým kvádrem. [Animace řešení] Úkol 2: V kosoúhlém promítání, které je dáno úhlem zkosení ω = 145° a poměrem zkreslení q=1/2, zobrazte kosoúhlý průmět bodu A o souřadnicích A[3,5,6] spolu s jeho souřadnicovým kvádrem. [Animace řešení] Úkol 3:  Zobrazte kvádr o rozměrech 3, 4 a 5 cm prostřednictvím těchto zobrazovacích metod: a) Volné rovnoběžné promítání. b) Kosoúhlé promítání (ω = 150°, 3/4). c) Kavalírní perspektiva (ω = 135°). d) Vojenská perspektiva (ω = 135°). (Dle vlastního uvážení zvolte pravotočivou nebo levotočivou soustavu souřadnic. Rýsujte!)

• Reálné a virtuální modely.
• Mnohostěny. Sítě mnohostěnů. Pravidelné mnohoúhelníky. Pravidelné a polopravidelné mnohostěny.

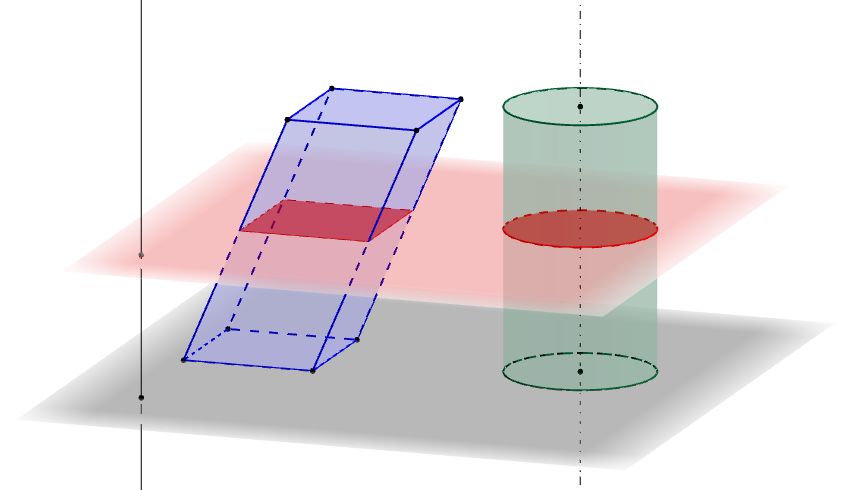
Pravidelné mnohostěny. Kapitoly 4.8 (pravidelné mnohoúhelníky), 5 (mnohostěny) Sítě těles: [Kosý hranol]   [Pětiboký jehlan]   Cavalieriho princip / Cavalieri's principle (Wikipedia)

• Řezy útvarů rovinou. Řešení stereometrických a aplikačních úloh.

Úkol 1:  V programu GeoGebra, konkrétně v Grafickém náhledu 3D, proveďte řez čtyřbokého jehlanu ABCDE rovinou FGH. Sestrojte tak, aby bylo možné měnit parametry jehlanu i roviny tažením myší. (Inspirace viz https://www.geogebra.org/m/mpe4dbfn) Úvod do středové kolineace a osové afinity / Středová kolineace (převzato z textu R. Hašek: Geometrie 4) / Osová afinita (převzato z textu R. 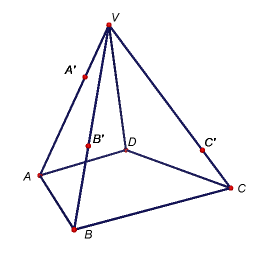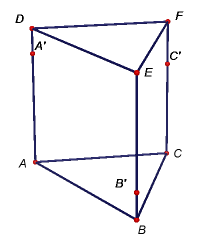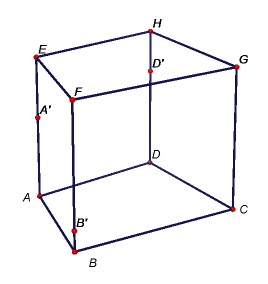Hašek: Geometrie 3) GeoGebra: [Středové promítání] [Středová kolineace] [Rovnoběžné promítání] [Osová afinita] Úkol 2:  V programu GeoGebra vytvořte modely těles dle níže uvedených obrázků i s popisem zobrazených bodů. Potom sestrojte řezy těchto těles rovinami určenými body A'B'C', resp. A'B'D'. 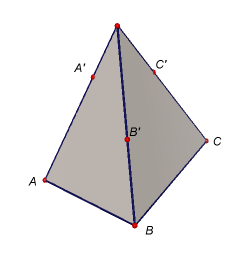Úkol 3:  Sestrojte řez kvádru ABCDA'B'C'D' rovinou MNP; M je vnitřní bod hrany CC', pro který platí 4|CM|=|CC'|, N je střed hrany A'D' a bod P leží na prodloužení hrany B'B za bod B a platí 3|BP|=|BB'|. (J. Polák: Přehled středoškolské matematiky, str. 481, Zadání v GeoGebře)




• Užití geometrického software k modelování trojrozměrných útvarů a řešení stereometrických úloh.

Literatura

[1]  Drábek, K., Harant, F., Setzer, O.:. Deskriptivní geometrie I, SNTL, Praha 1978.
[2]  Kargerová, M., Deskriptivní geometrie- pro technické školy vysoké, vyšší a střední. Montanex, Praha, 2007.
[3]  Pomykalová, E., Deskriptivní geometrie pro střední školy. Prometheus, Praha, 2010.
[4]  Urban, A.:. Deskriptivní geometrie I, SNTL, Praha 1982.
[5]  Doležal, J.:. Základy geometrie a Geometrie, VŠB-TU Ostrava, on-line učebnice
      [http://mdg.vsb.cz/jdolezal/StudOpory/Uvod.html].
[6]  Pomykalová, E., Matematika pro gymnázia - Stereometrie. Prometheus, Praha, 1995.
[7]  Voráčová a kol., Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha, 2012.
[8]  Vrba, A.: Cabri 3D v2 Příručka pro uživatele.
      Online: http://www.pf.jcu.cz/cabri/cabri3d/download/Cabri_3D_prirucka.pdf

Internetové odkazy

Software ke stažení

sketchup.google.com ... aplikace Google SketchUp (možnost bezplatného stažení)
www.geogebra.org ... program GeoGebra (možnost bezplatného stažení)
www.rhino3d.com ... 3D modelovací program Rhinoceros
Dalest Elica ... podpora výuky stereometrie
dg.vidivici.cz ... Program Deskriptivní geometrie

Materiály pro výuku a sebevzdělávání

i2geo.net ... portál pro sdílení výukových materiálů dynamické geometrie
wiki.geogebra.org ... GeoGebra Wiki - manuál, výukové materiály, fórum apod.
wiki.geogebra.org/cs/ ... postupně překládaná česká verze GeoGebra Wiki
www.youtube.com/user/GeoGebraChannel ... GeoGebra na YouTube
www.geogebratube.org ... Materiály v GeoGebře ke stáhnutí
http://www.korthalsaltes.com ... Paper models of polyhedra

Požadavky na studenta

• Zápočet.
  Předmět je ukončen zápočtem. Podmínkou jeho splnění je úspěšné prokázání znalostí z předmětu diskusí nad otázkou vylosovanou z tohoto přehledu: Otázky 3G3Z.