Kurz užití programu GeoGebra I

Kurz DVPP akreditovaný MŠMT v rámci systému dalšího vzdělávání pedagogických pracovníků pod č. j.: 16 700/2012-25-283



Obsah kurzu

  1. Úvod do programu GeoGebra
  2. Prostředí programu GeoGebra
    • Nákresna + Algebraické okno
      • Konstrukční úlohy

        Příklad 1:  V rovině je dán libovolný trojúhelník ABC. Uvažujme bod D této roviny a spusťme z něj kolmice na strany trojúhelníku ABC, případně jejich prodloužení. Ptáme se, zda existuje taková poloha bodu D, pro kterou leží paty těchto kolmic v jedné přímce.
        (Paty kolmic leží v přímce právě tehdy, když bod D náleží kružnici opsané trojúhelníku ABC. Tato přímka se nazývá Simsonova přímka.)

        Příklad 2: V libovolném trojúhelníku, který není rovnoramenný, se protíná osa jeho libovolné strany s osou protějšího vnitřního úhlu v bodě kružnice trojúhelníku opsané. (Kuřina, F. Umění vidět v matematice. Praha: SPN, 1989. Str. 146.)
        Uvedené tvrzení znázorněte dynamickým obrázkem, který potom využijte k prezentaci důkazu.

        Příklad 3: Jsou dány tři různé rovnoběžné přímky a, b, c a bod A, který leží na přímce a. Sestrojte všechny rovnostranné trojúhelníky ABC, jejichž vrcholy B, C leží po řadě na přímkách b, c. Úlohu vyřešte. Potom proveďte vhodné krokování konstrukce tak, aby mohla být přehrávána a materiál převeďte do formátu dynamického pracovního listu.

      • Graf funkce

        Příklad 4: Zobrazte graf funkce f:y=x3-2x2+1. Sestrojte tečnu grafu funkce f nejprve v bodě x=3, potom v bodě x=a.

        Příklad 5:  Vyšetřete vliv parametrů a, b, c na průběh grafu funkce:

        • f:y=ax+b,
        • g:y=a(x-b)2+c,
        • h:y=asin(bx+c).
        U každé funkce zobrazujte v Nákresně její aktuální předpis.

        Příklad 6:  Sestrojte graf funkce f(x), která je definovaná po částech: f(x)=-1 pro x<-3, f(x)=x2-3 pro -3≤x≤2 a f(x)=ln(x-1)+1 pro x≥2.

      • Analytická geometrie

        Příklad 7:  Zobrazte elipsu danou rovnicí (x-2)2/4+(y+1)2/9=1. Poté zobecněte použitím posuvníků.

        Příklad 8:  Trajektorie bodu pevně spojeného s kružnicí odvalující se po přímce se nazývá cykloida. Vytvořte animaci vzniku cykloidy.

      • Omezená nabídka nástrojů.

        Příklad 9:  Redukujte nabídku nástrojů na minimum nutné k eukleidovské konstrukci osy úsečky.

        Příklad 10:  Geoboard.

      • Množina bodů dané vlastnosti.

        Příklad 11:  Určete množinu poloh ortocentra trojúhelníku ABC, jestliže se jeho vrchol C pohybuje po přímce p rovnoběžné s AB.

      • Obrázky na pozadí.

        Příklad 12: Určete typ křivky na obrázku. Pokuste se najít její rovnici: Fontána.

        Příklad 13: Na fotografii je zachycena část dlažby na podlaze kostela Sv. Jana Nepomuckého na Zelené hoře u Žďáru nad Sázavou. Najděte a znázorněte všechny rovinné transformace, v nichž se na sebe některé dlaždic zobrazují.

        Dlažba

        Příklad 14:  Tři přátelé z Českých Budějovic, Brna a Prahy se chtějí setkat. Hledají proto místo, jehož vzdálenost bude pro všechny přijatelná. Vytvořte si grafický soubor s mapou České republiky vhodné velikosti, vložte si ji do Nákresny programu GeoGebra a pomocí jeho nástrojů v ní najděte takové místo, že

        1. jeho vzdálenosti od tří uvedených měst jsou stejné,
        2. součet jeho vzdáleností od tří uvedených měst je minimální.
        (Příklad je převzat z materiálu 5.)

    • CAS
    • Tabulka

      • Příklad 18:  "... na hliněné tabulce z Mezopotámie, která pochází z období kolem roku 1700 před Kristem a nyní je vystavena v Louvru, je zadán následující problém: Za jak dlouho se zdvojnásobí výše vkladu při dvacetiprocentní roční úrokové míře (uvažujeme složené úrokování)? " (Eli Maor: e: The story of a number)
        Úlohu vyřešte a pokuste se vymyslet, jak problém řešili v Mezopotámii v době vzniku tabulky.

        Příklad 19:  Uvažujte obdélník o konstantním obvodu. Pro jaký poměr délek jeho stran a, b je jeho obsah maximální?.

        Příklad 19 (b):  Na obrázku je znázorněn list papíru, který je přehnut tak, že levý horní roh se dotýká spodního okraje v bodě P ve vzdálenosti x od levého dolního rohu. Představte si všechny možné takovéto polohy bodu P. Pro jaké x je obsah vyšrafovaného trojúhelníku na obrázku maximální?

        List papíru

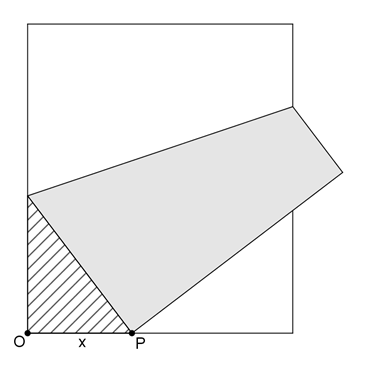
    • 3D

      • Příklad 20: Sestrojte pravidelný pětiboký hranol a vytvořte jeho síť. Poté síť skryjte a sestrojte řez hranolu rovinou, jejíž sklon budeme moci měnit.

        Příklad 21:  Je dán pravidelný čtyřboký hranol ABCDA’B’C’D’; |AB|=4 cm, |AA’|= v = 5,5 cm. Bod M je středem hrany A’D’. Vypočtěte vzdálenost bodu B od přímky CM. (E. Pomykalová: Matematika pro gymnázia, Stereometrie, Prométheus, 2011)
        Řešení

    • Pravděpodobnostní kalkulačka

      • Příklad 22: Velkoobchodní sklad zásobuje 10 obchodů. Od každého z nich může přijít objednávka na příští den s pravděpodobností 0.4, nezávisle na objednávkách ostatních obchodů. Jaká je pravděpodobnost, že sklad obdrží 6 objednávek?.



Literatura

  1. Günzel, M. a kol.: Integrace elektronických prostředí pro počítačem podporovanou výuku matematiky. Jihočeská univerzita v Č. B., 2012. Dostupné z http://home.pf.jcu.cz/~ippvm/archives/category/publikace
  2. Hohenwarter, M., Hohenwarter, J. Introduction to GeoGebra, Version 4.4 Dostupné z http://www.geogebra.org/book/intro-en.pdf
  3. Hašek, R., Petrášková, V. GeoGebra in financial education. North American GeoGebra Journal, Vol. 2, No. 1, 2013, Miami University, USA, ISSN: 2162-3856, pp. 31-36. Dostupné z http://www.ggbmidwest.com
  4. Hašek, R. Numerical analysis of a planar motion; GeoGebra as a tool of investigation. North American GeoGebra Journal (ISSN: 2162-3856). Miami University, Oxford, OH, USA. Vol. 1, No. 1, 2012. pp. 33 - 36. Dostupné z http://www.ggbmidwest.com
  5. Pöchtrager, H. Maths in real life, Neue Mittelschule St. Peter am Wimberg, Austria.



Internetové odkazy

GeoGebra
www.geogebra.org
wiki.geogebra.org ... GeoGebra Wiki - manuál, výukové materiály, fórum apod. (postupně překládaná česká verze: wiki.geogebra.org/cs/)
www.youtube.com/user/GeoGebraChannel ... GeoGebra na YouTube
www.geogebratube.org ... Materiály v GeoGebře ke stáhnutí

Dynamická geometrie
i2geo.net ... I2G Intergeo - mezinárodní portál pro sdílení materiálů dynamické geometrie

Matematika kolem nás
Maths in the City
Plus magazine ... living mathematics



Roman Hašek, katedra matematiky PF JU, kontakt: hasek@pf.jcu.cz