GEOMETRIE II (KMA/7G2) |
Předmět je zaměřen na kuželosečky a kvadratické plochy.
Osnova
-
Úvod do předmětu.
Kuželosečky a kvadratické plochy - představení
-
Kuželosečky
GeoGebra: Řez kuželové plochy rovinou
- Kuželosečky regulární a singulární.
- Vybrané kvadratické plachy a jejich zobrazení v programu GeoGebra (kuželová plocha, válcová plocha, rotační paraboloid, rotační hyperboloid, ...)
Kružnice
- Definice: Množina bodů v rovině, jejichž vzdáleností daného bods S je konstantní.
- Rovnice kružnice (středová, parametrická, polární)
Elipsa
- Definice: Množina bodů v rovině, jejichž součet vzdáleností od dvou daných bodů F1 a F2 je konstantní.
- Rovnice elipsy (kanonická, středová), viz [1] (Kuželosečky), str. 8-10
- Zahradnická konstrukce elipsy
- Další úlohy na elipsu jako množinu bodů daných vlastností
-
Kočka na žebříku
- Proužková konstrukce elipsy - součtová a rozdílová
-
ÚKOL: Je dána kružnice k se středem S a uvnitř ní bod M. Určete množinu středů kružnic procházejících bodem M a dotýkajících se kružnice k.
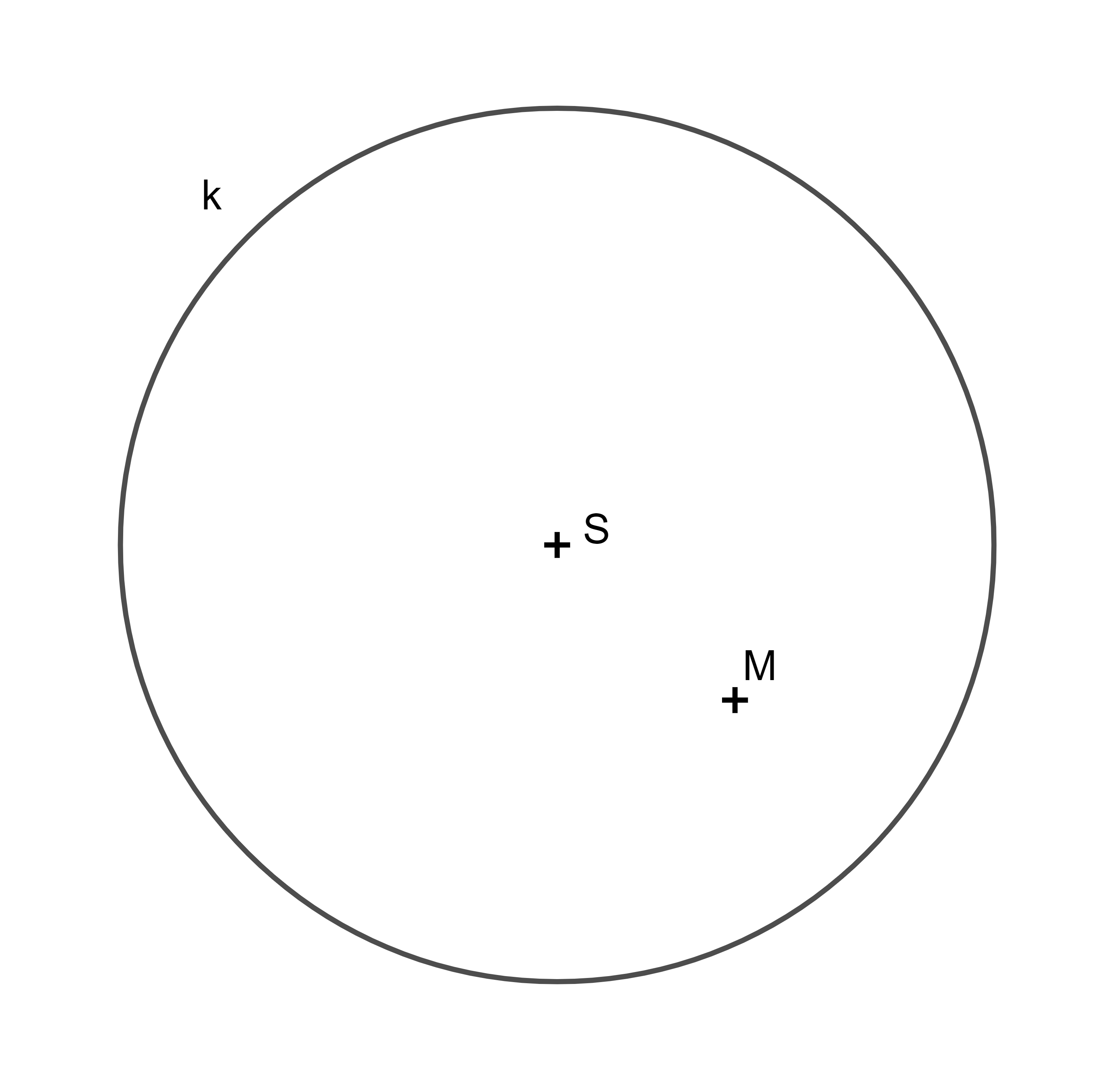
-
Kočka na žebříku
Hyperbola
- Definice: Množina bodů v rovině, pro které je absolutní hodnota rozdílu jejich vzdáleností od dvou daných bodů F1 a F2 konstantní.
- Rovnice hyperboly (kanonická, středová), viz [1] (Kuželosečky), str. 28-29
- Parametrické rovnice hyperboly; hyperbolický sinus a kosinus, řetězovka,
viz https://en.wikipedia.org/wiki/Hyperbola, https://en.wikipedia.org/wiki/Catenary - Nepřímá úměrnost. Grafem funkce nepřímá úměrnost je rovnoosá hyperbola s asymptotami v souřadnicových osách.
ÚKOL: Napište v kanonickém tvaru rovnici hyperboly, která je grafem funkce $f:\,y=\dfrac{1}{x}$, tj. pro umístění vůči soustavě souřadné takové, že střed hyperboly je totožný s jejím počátkem a osy hyperboly leží v souřadnicových osách $x$, $y$.
Parabola
- Definice: Množina bodů v rovině, které mají od daného bodu F a dané přímky p stejnou vzdálenost. Bod F nazýváme ohniskem paraboly, přímku d pak její řídící přímkou.
- Rovnice hyperboly (kanonická, vrcholová), viz [1] (Kuželosečky), str. 45-46
Úlohy k procvičení
Řešte úlohy 5.23, 5.27, 5.29, 5.30, 5.41, 5.42, 5.51, 5.52 a 5.53 z [3], viz Kuzelosecky_Cv_1.pdf, Kuzelosecky_Cv_2.pdf , Kuzelosecky_Cv_3.pdf.
Oskulační kružnice kuželosečky
Oskulační kružnicí rozumíme kružnici, která se dotýká uvažované křivky v bodě, v němž s ní má společnou tečnu a ze všech takových kružnic se ke křivce nejvíce přimyká.
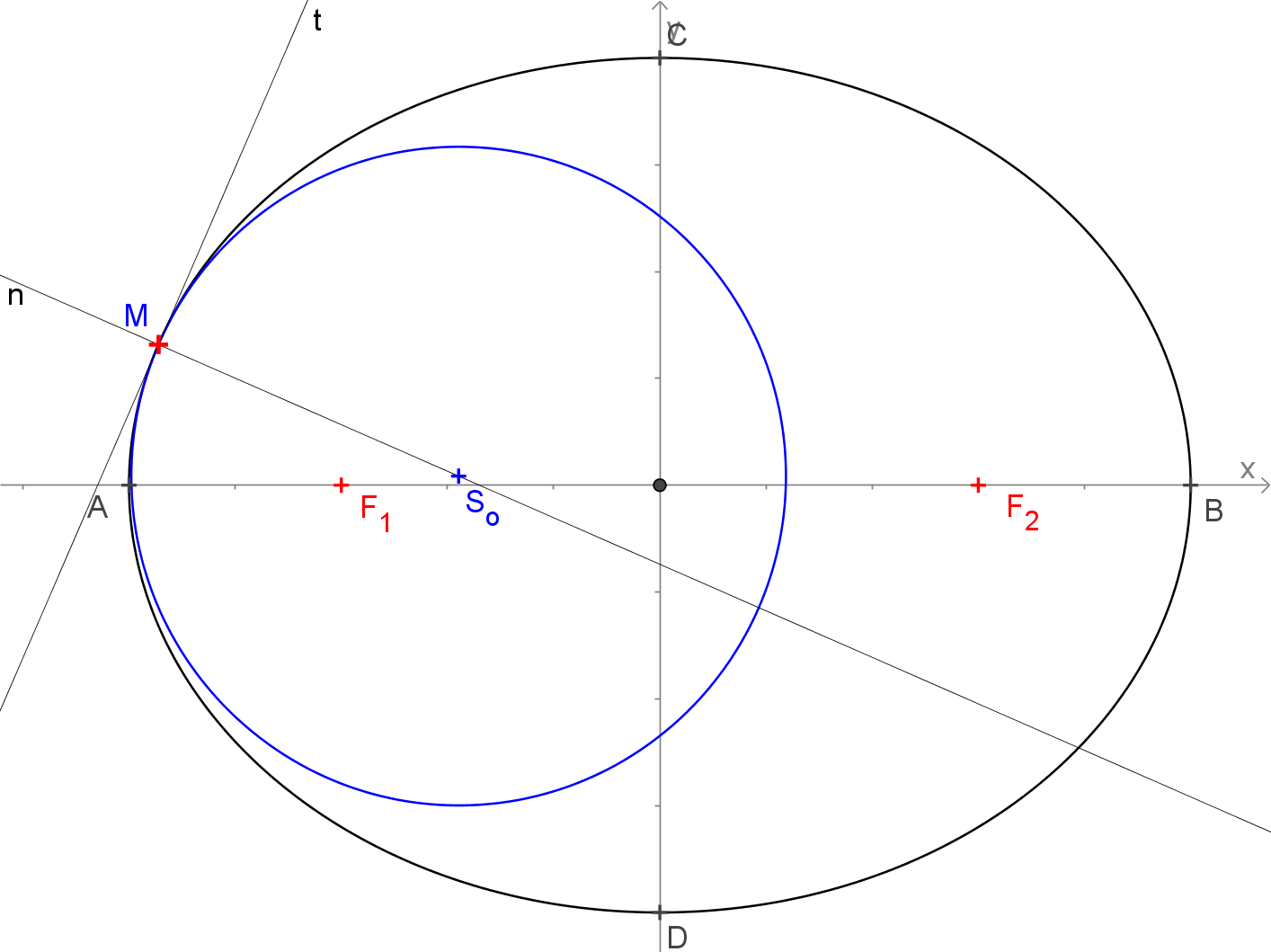
Poloměr R oskulační kružnice v konkrétním bodě křivky nazýváme poloměrem křivosti v tomto bodě. Převrácenou hodnotou tohoto poloměru je potom křivost křivky v daném bodě, značíme ji k.
Oskulační kružnice ve vrcholech elipsy jsou výjmečné tím, že mají s elipsou společný právě jeden bod, onen vrchol. Proto se jim často říká hyperoskulační kružnice, případně superoskulační kružnice.
Konstrukce středů oskulačních kružnic regulárních kuželoseček.png)
.png)
.png)
-
Konstrukce kuželoseček
Zahradnická konstrukce elipsy
[1] (Kuželosečky) (str. 12)
Trojúhelníková a proužková konstrukce kuželosečky
[1] (Kuželosečky) (str. 13-15)
Bodová konstrukce kuželosečky
[1] (Kuželosečky): elipsa (str. 10), hyperbola (str. 31), parabola (str. 46) / GeoGebra applety: [elipsa] [hyperbola] [parabola]
Tečna kuželosečky (kružnice, elipsy, hyperboly, paraboly)
-
Tečna kuželosečky daného směru
Příklad: Napište rovnice tečen kružnice $x^{2}+y^{2}-16=0$ rovnoběžných s přímkou $y=3x$.
-
Tečna kuželosečky v bodě dotyku T[m, n]
GeoGebra applet: [Tečna kuželosečky v daném bodě]
-
Tečna kuželosečky z bodu P[m, n]
Příklad: Určete body dotyku tečen vedených bodem $P[0; 0]$ ke kružnici s rovnicí $x^{2}+y^{2}+10x+10y+49=0$.
Příklady k řešení
Domácí úkol: [1] (Kuželosečky): Str. 25/Cvičení 6, 7, 8.
Polára p bodu P vzhledem ke kuželosečce
Polárou bodu P vzhledem ke kuželosečce rozumíme přímku p. Bod P nazýváme pólem. Pro vnější body je to přímka spojující body dotyku tečen vedených z tohoto bodu ke kuželosečce.
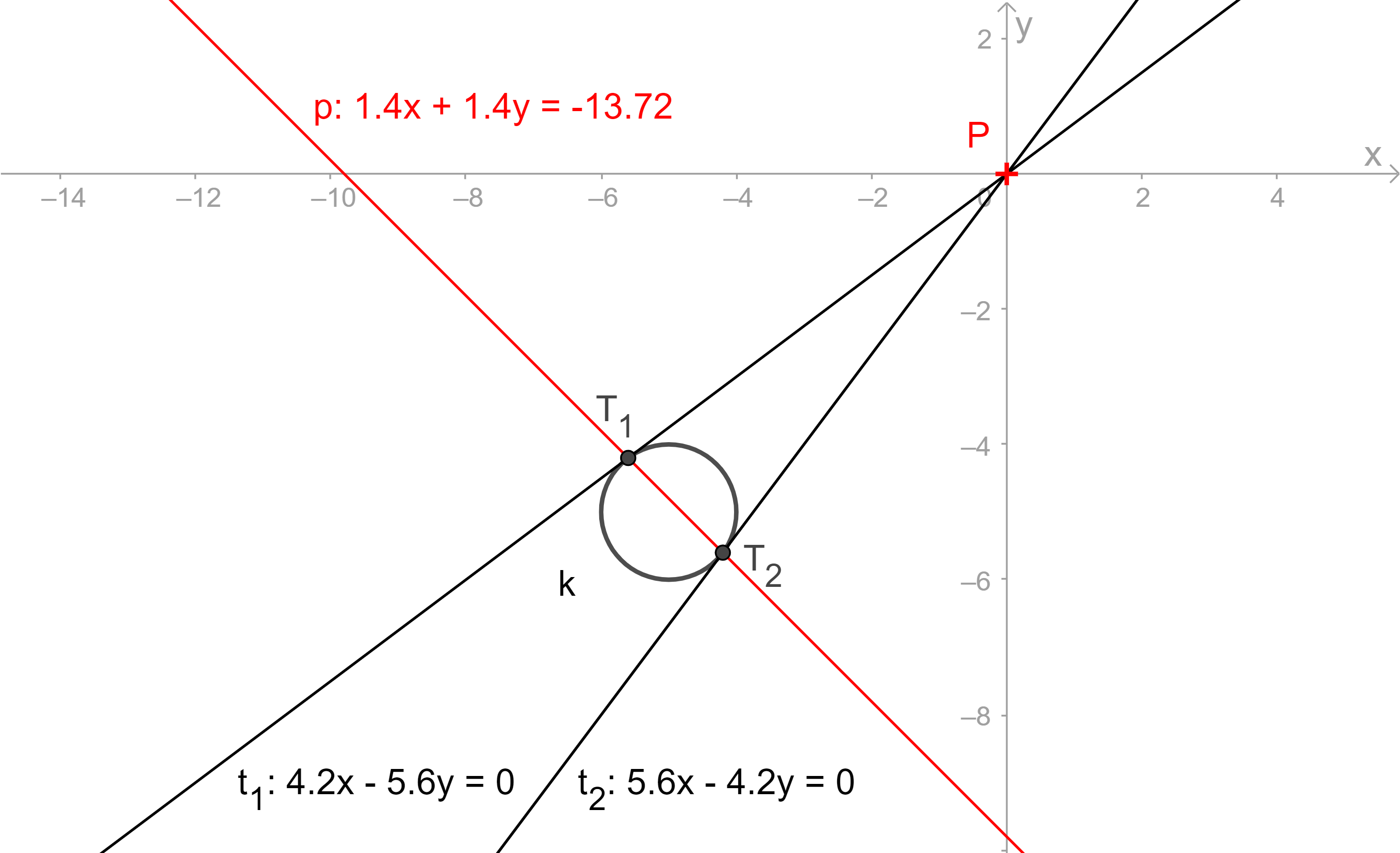
- GeoGebra applet: [Pól a polára vzhledem ke kuželosečce]
Konstrukci poláry vzhledem k vnitřnímu bodu pak napomůže následující věta.
Věta: Nechť p je polára bodu P a q je polára bodu Q. Pokud Q leží na p, potom q prochází bodem P.
- Úkol: Sestrojte poláru m bodu M ležícího uvnitř kružnice k.
-
Tečna kuželosečky daného směru
-
Ohniskové vlastnosti kuželoseček
- Elipsa
ÚKOL: Shlédněte video Lithotripsy (litotripse) a interpretujte ho s důrazem na příslušnou vlastnost elipsy.
Věta: Tečna elipsy půlí vnější úhly průvodičů bodu dotyku.
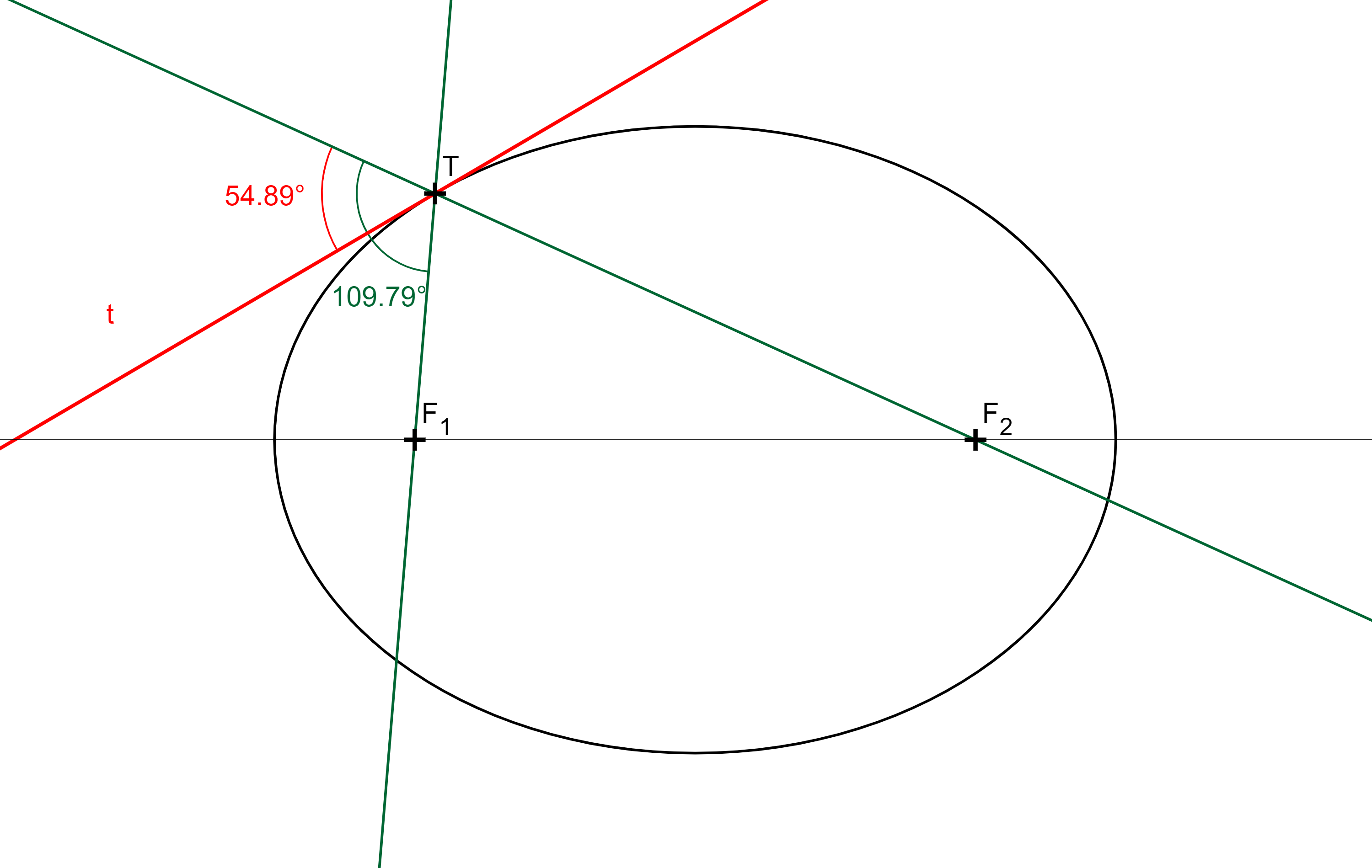
GeoGebraDůkaz: Pech, P. Kuželosečky, str. 20.
GeoGebra: Naznačení důkazu pomocí zákona odrazu
Aplikace: Whispering gallery, Feynman's lost lecture, Pech, P. Kuželosečky, Příklad na str. 23-24.
Věta: (Řídící kružnice elipsy) Množina všech bodů souměrně sdružených s jedním ohniskem elipsy podle jejích tečen je kružnice se středem v druhém ohnisku a o poloměru rovném velikosti hlavní osy elipsy (tj. 2a).
Poznámka: Řídící kružnice jsou dvě, se středy v obou ohniscích elipsy.
Věta: (Vrcholová kružnice elipsy) Množina všech pat kolmic spuštěných z ohnisek elipsy na její tečny je kružnice opsaná kolem středu elipsy s poloměrem rovným délce hlavní polosy (tj. a).
Příklady k řešení
ÚKOL 1 (Ohniskové vlastnosti elipsy).pdf ; {Řešení: Příklad 1, Příklad 2, Příklad 3, Příklad 4}
-
Hyperbola
Věta: Tečna hyperboly půlí vnější úhly průvodičů bodu dotyku.
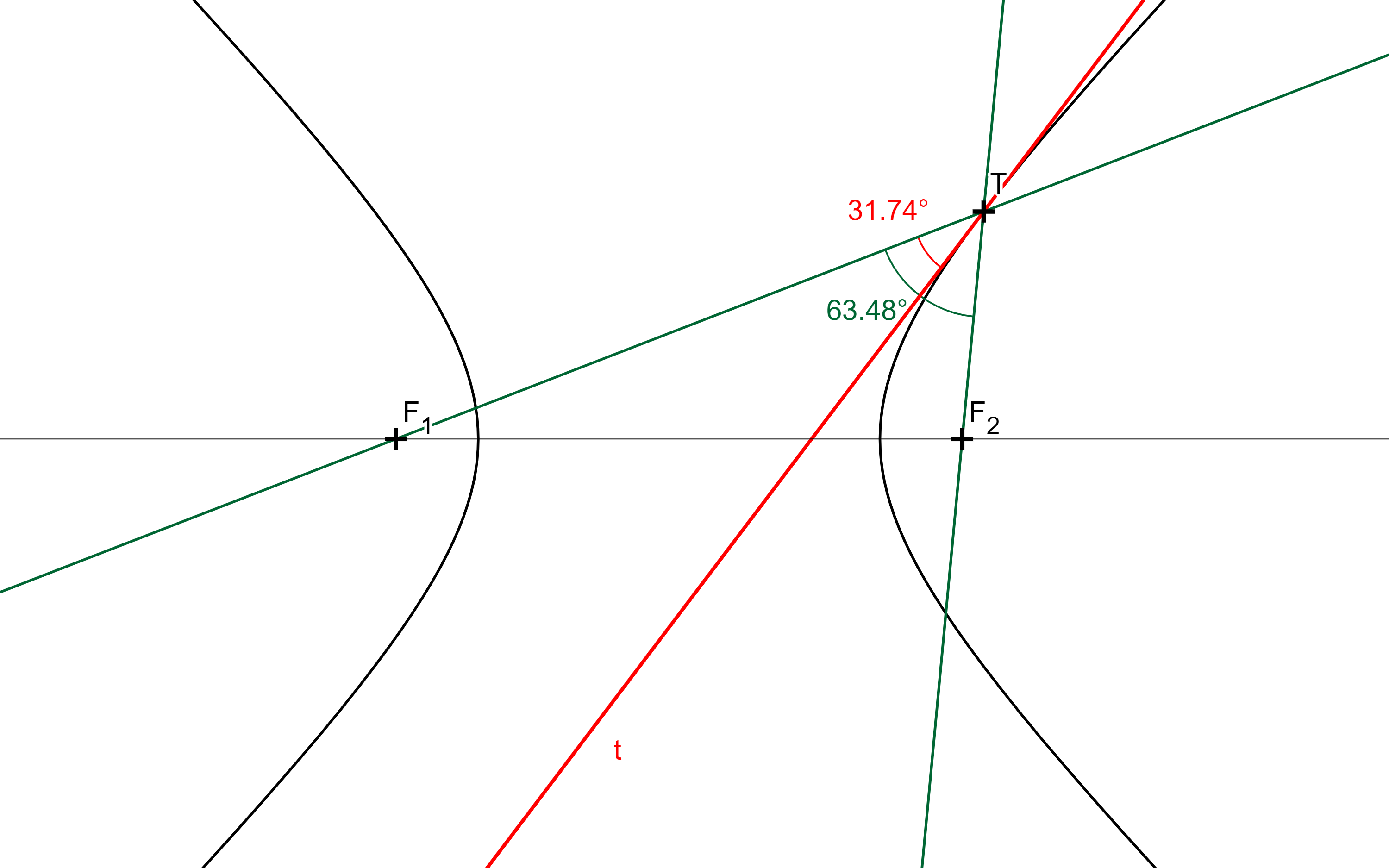
GeoGebra
GeoGebra applet: Ilustrace odrazem od tečny hyperboly
Důkaz: Pech, P. Kuželosečky, str. 35.
Věta: (Řídící kružnice hyperboly) Množina bodů souměrných s jedním ohniskem hyperboly podle všech jejích tečen leží na kružnici se středem v druhém ohnisku a s poloměrem rovným velikosti hlavní osy hyperboly (tj. 2a). Tuto kružnici nazýváme řídící kružnicí hyperboly.
Poznámka 1: Hyperbola má dvě řídící kružnice, se středy v obou jejích ohniscích, viz níže uvedený obrázek (a dynamický applet), kružnice $g_{1}(F_{1}, 2a)$, $g_{2}(F_{2}, 2a)$.
Poznámka 2: Množina bodů uvedené vlastnosti není s řídící kružnicí identická. Na každé z řídících kružnic totiž existují dva body, které nemohou být obrazem příslušného ohniska v osové souměrnosti podle žádné z tečen hyperboly, viz obrázek (a jemu příslušný applet), body $Q_{1}, Q_{2}$ na $g_{2}$ a $Q_{3}, Q_{4}$ na $g_{1}$. Dokážete vysvětlit, jak tyto body určíme?
Věta: (Vrcholová kružnice hyperboly) Množina pat kolmic spuštěných z ohnisek hyperboly na všechny její tečny lrží na kružnici opsané kolem středu hyperboly s poloměrem rovným délce hlavní polosy (tj. a). Tuto kružnici nazýváme vrcholovou kružnicí hyperboly (prochází vrcholy hyperboly), viz kružnice $v(S, a)$ na obrázku.
Poznámka: Ani tato kružnice není s příslušnou množinou bodů dané vlastnosti identická. I na ní leží body, které nemohou být patami žádných kolmic spuštěných z ohnisek na tečny hyperboly, viz body $R_1$, $R_2$, $R_3$, $R_4$ na obrázku níže (a v příslušném appletu). Dokážete vysvětlit, jak tyto body určíme?
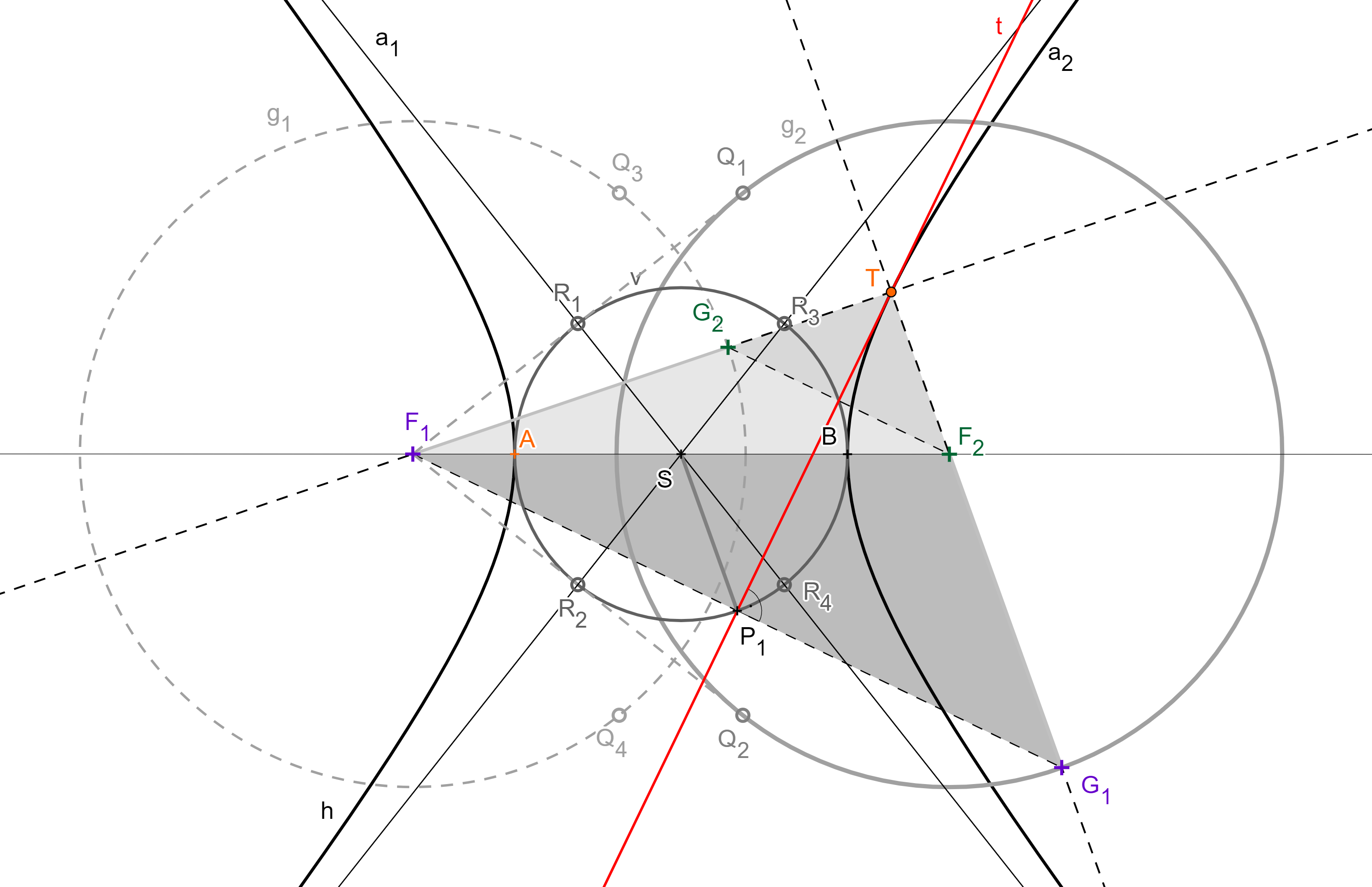
GeoGebraDůkaz: Pech, P. Kuželosečky, str. 37-39.
-
Parabola
Věta: Tečna paraboly půlí vnější úhly průvodičů bodu dotyku (jedním z průvodičů je přímka určená bodem dotyku a ohniskem, druhým pak je kolmice spuštěná z bodu dotyku na řídící přímku).
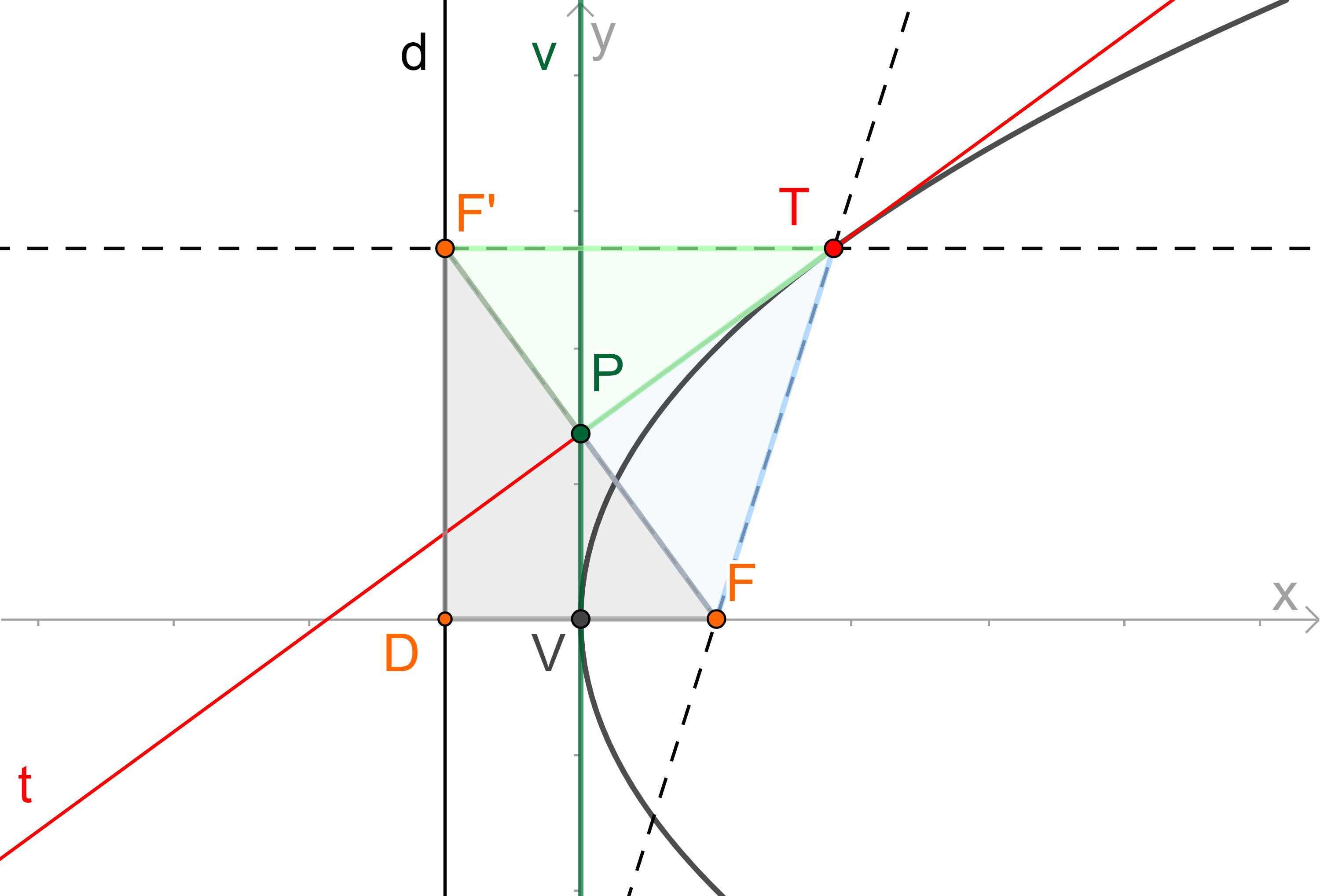
GeoGebra
Důkaz: Pech, P. Kuželosečky, str. 50.
Praxe viz např. Novinky.cz: Za požár v domě mohlo kosmetické zrcátko.
GeoGebra applet: Ilustrace odrazem od tečny paraboly
Věta: (Řídící přímka paraboly) Množina bodů souměrných s ohniskem paraboly podle všech jejích tečen je řídící přímka $d$.
Věta: (Vrcholová tečne paraboly) Množina pat kolmic spuštěných z ohniska paraboly na všechny její tečny je vrcholová tečna $v$.
Důkaz: Pech, P. Kuželosečky, str. 52.
Příklady k řešení
ÚKOL 2 (Ohniskové vlastnosti paraboly).pdf; {Řešení: Příklad 1, Příklad 2}
Poznámka: Při řešení druhého příkladu využijte druhou z vět uvedených na str. 53 skript Pech, P. Kuželosečky.
- Elipsa
-
Quételetova-Dandelinova věta
Quételetova-Dandelinova věta pro válcovou plochu: Řez rotační válcové plochy rovinou, která je kosá k ose plochy, je elipsa. Jejími ohnisky jsou dotykové body kulových ploch, které jsou válcové ploše vepsány a dotýkají se roviny řezu. Délka její vedlejší poloosy se rovná poloměru válcové plochy ([1], str. 187).
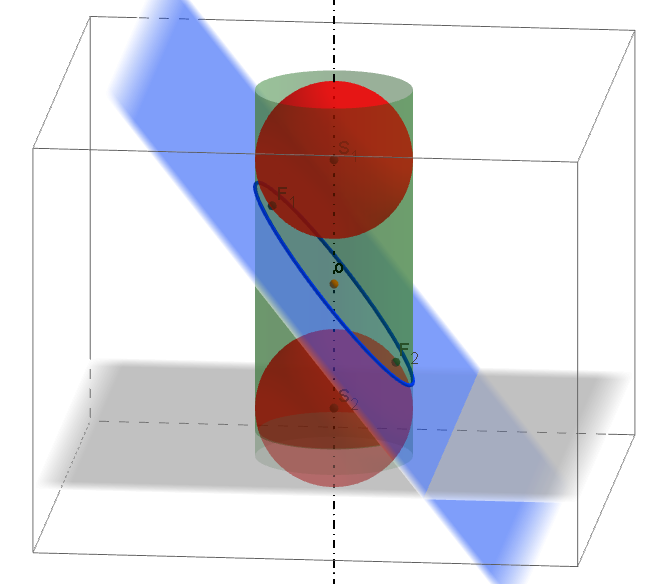
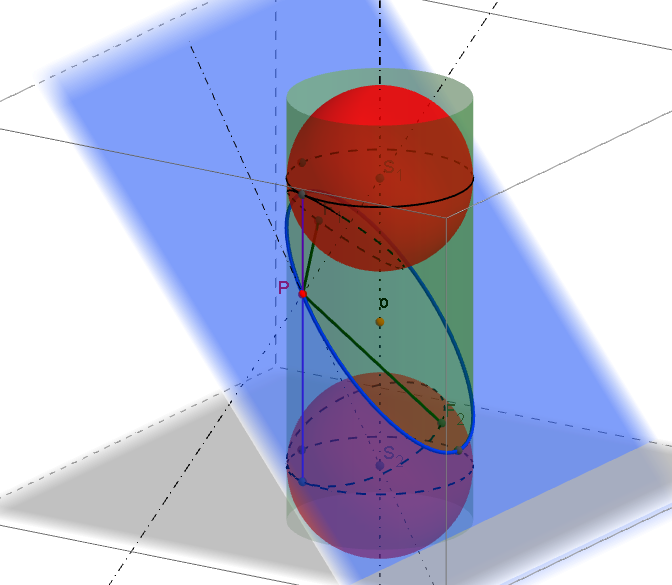
Quételetova-Dandelinova věta pro válcovou plochu a její důkazQuételetova-Dandelinova věta pro kuželovou plochu: Rovina, která naní vrcholová, ani není kolmá k ose a která s rovinou povrchové kružnice rotační kuželové plochy svírá úhel menší než povrchové přímky plochy, protíná rotační kuželovou plochu v elipse. Jejími ohnisky jsou dotykové body kulových ploch, které jsou vepsány kuželové ploše a dotýkají se roviny řezu ([1], str. 208).
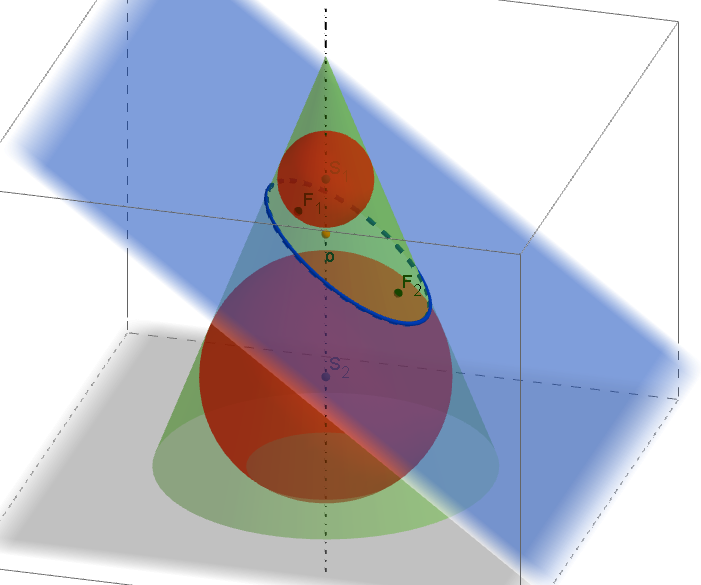
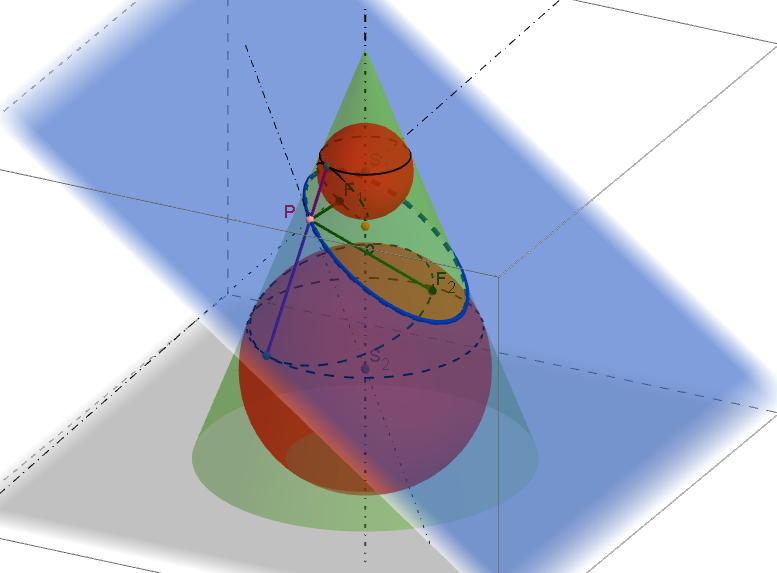
Quételetova-Dandelinova věta pro kuželovou plochu a její důkaz -
Řídící přímka kuželosečky
Každou regulární kuželosečku s výjimkou kružnice lze vytvořit jako množinu bodů v rovině, které mají od daného bodu F této roviny a od dané přímky d této roviny, přičemž F neleží na d, stálý poměr vzdáleností rovný kladnému číslu ε. Přímka d je řídící přímka kuželosečky, F je její ohnisko. Číslo ε je číselná výstřednost (numerická excentricita) kuželosečky. Pro ε rovno 1 je vzniklá kuželosečka parabola, pro ε větší než 1 hyperbola a pro ε menší než 1 elipsa.
Pro elipsu a hyperbolu platí: $\epsilon = \dfrac{e}{a}.$
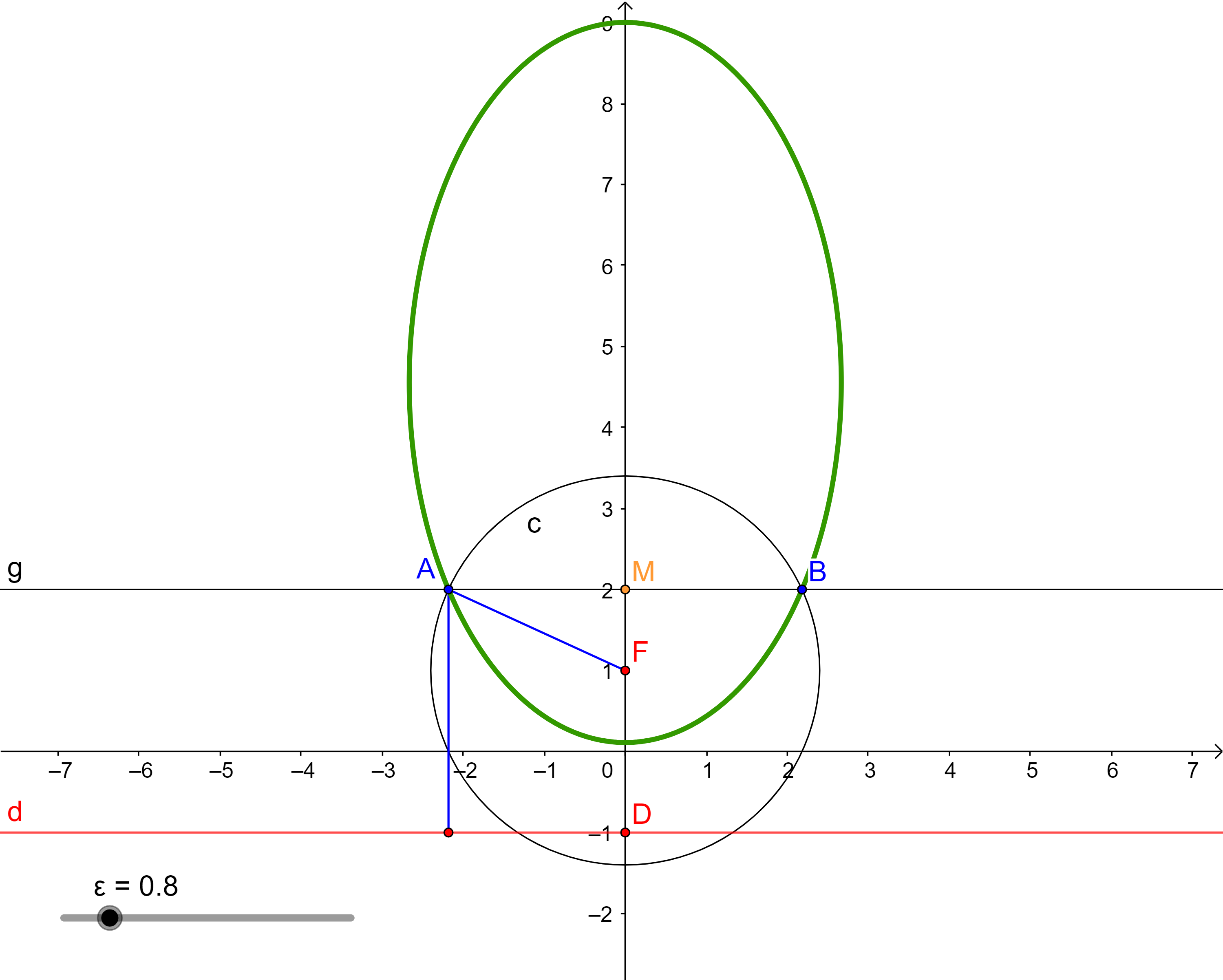
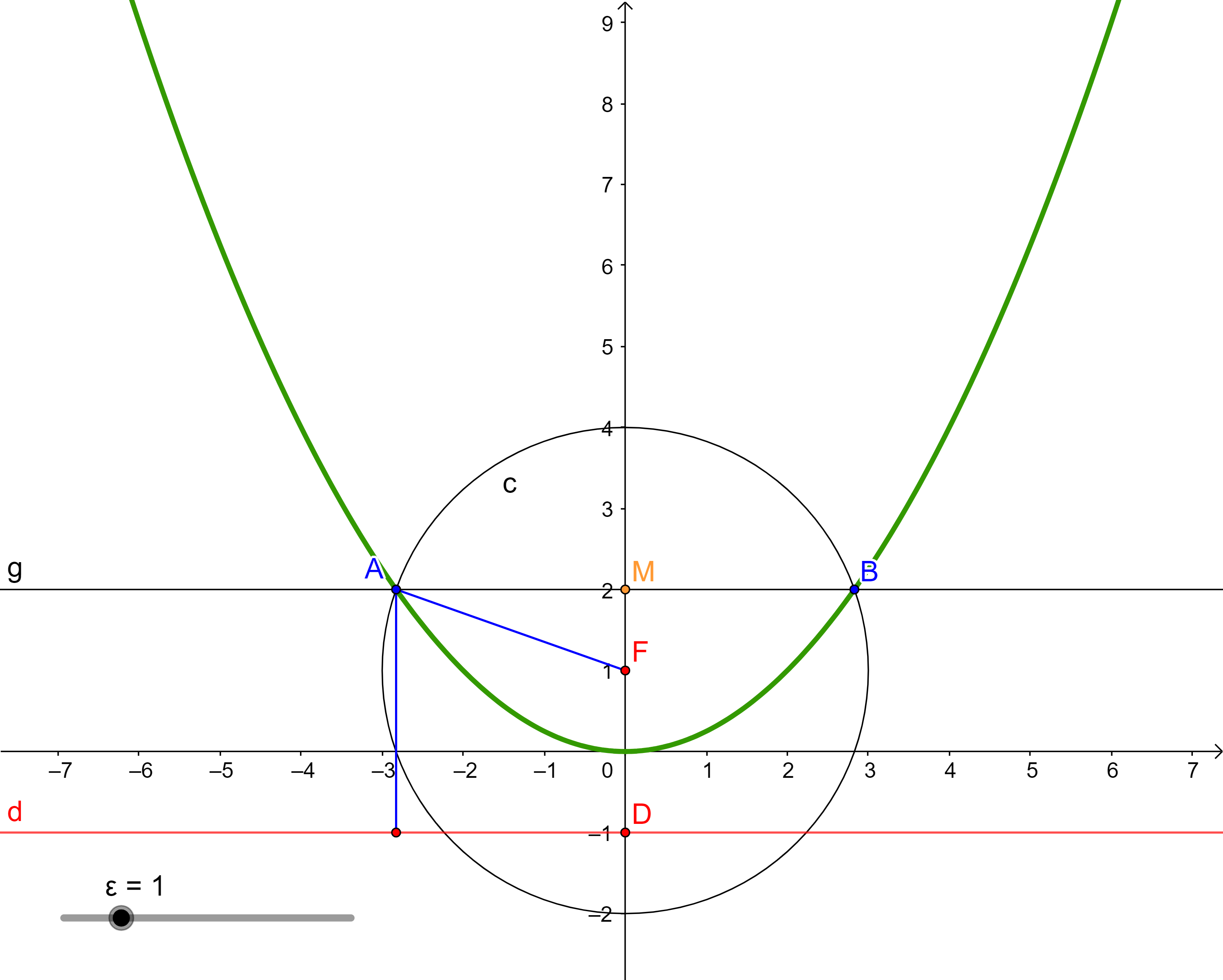
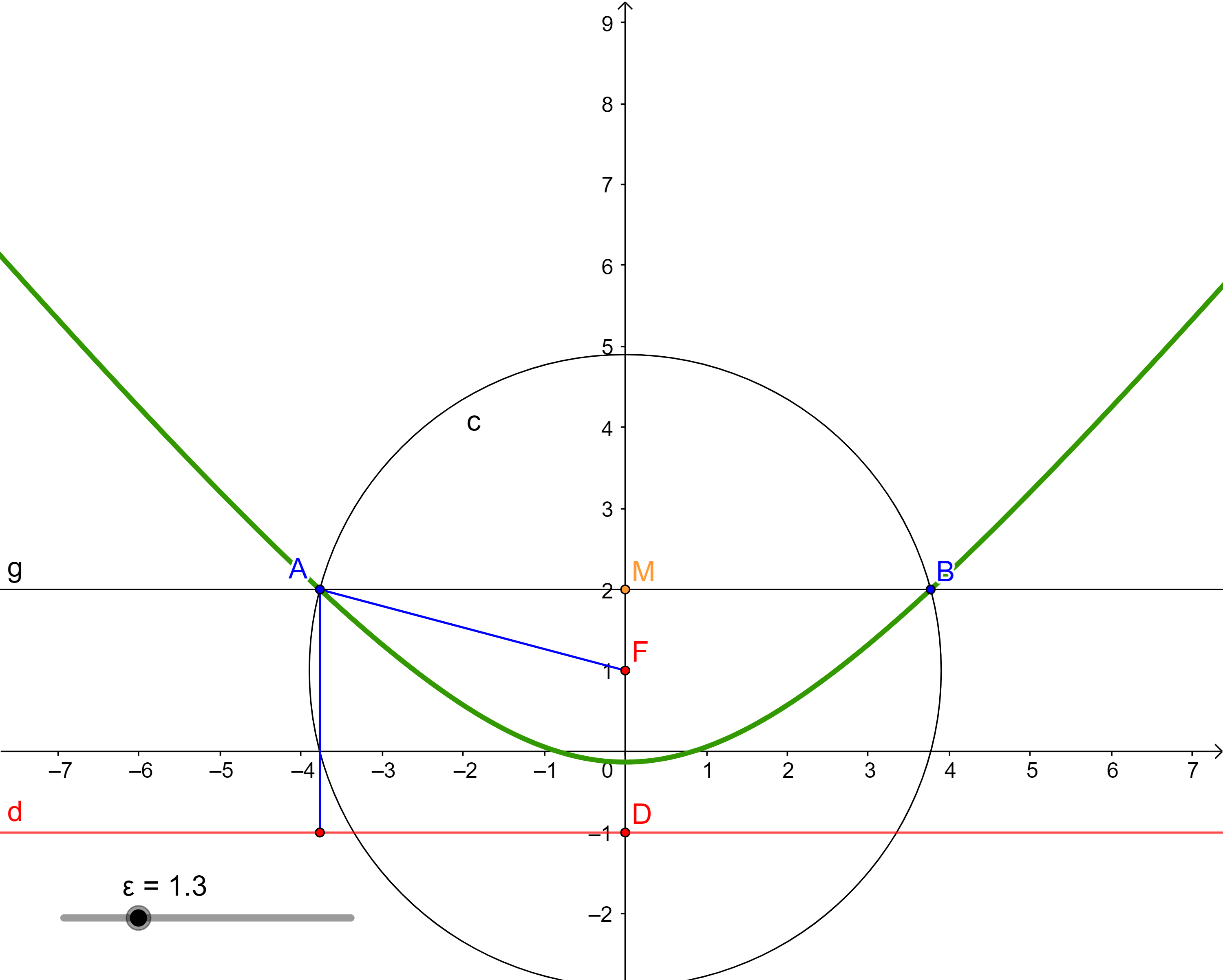
GeoGebra applet: [Kuželosečka daná řídící přímkou a ohniskem] -
Kuželosečka jako algebraická křivka 2. stupně
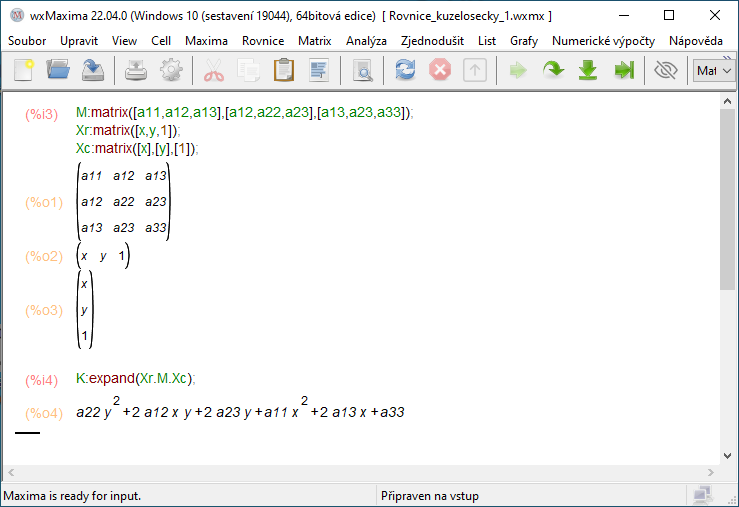
-
Kanonický tvar rovnice kuželosečky pomocí otočení.
wxMaxima: Algebraická rovnice kuželosečky / wxMaxima download
GeoGebra: Uvedení rovnice na kanonický tvar
Úplná klasifikace kuželoseček
-
eliptický typ
- elipsa (reálná)
- imaginární elipsa
- jediný bod (jako průsečík dvojice imaginárních přímek)
-
hyperbolický typ
- hyperbola
- dvojice různoběžek
-
parabolický typ
- parabola
- rovnoběky různé
- rovnoběky splývající
- rovnoběky imaginární
-
eliptický typ
-
Asymptotický směr kuželosečky

GeoGebra: Středový průmět rovnoběžek (různoběžek)
GeoGebra: Středový průmět kružnice - asymptotické směry
Přímka vs. kuželosečka
Detailní rozbor viz Pech, P. Kuželosečky, str. 90-94.
GeoGebra: Vzájemná poloha přímky a kuželosečky (hyperboly)
GeoGebra: Vzájemná poloha přímky a kuželosečky - obecně
Viz Pech, P. Kuželosečky, Věta na str. 93.
ÚKOL: Řešte cvičení 5 b na str. 100 v Pech, P. Kuželosečky.
-
Střed kuželosečky
Detailní rozbor viz Pech, P. Kuželosečky, str. 94-99.
Kuželosečky středové a nestředové.
ÚKOL: Určete střed kuželosečky z cvičení 5 b na str. 100 v Pech, P. Kuželosečky. Určete rovnice asymptoto této kuželosečky.
-
Tečna a polára kuželosečky. Sdružené průměry.
Tečna v bodě kuželosečky
ÚKOL: Řešte cvičení 5 na str. 121 v Pech, P. Kuželosečky.
Viz Pech, P. Kuželosečky, str. 113-116.
Polára. Tečna z bodu ke kuželosečce
ÚKOL: Řešte cvičení 8 na str. 121 v Pech, P. Kuželosečky.
Viz Pech, P. Kuželosečky, str. 116-120.
Sdružené průměry kuželosečky
GeoGebra: Sdružené průměry elipsy / GeoGebra: Sdružené průměry hyperboly / GeoGebra: Sdružené průměry paraboly
ÚKOL: Řešte cvičení 2 na str. 127 v Pech, P. Kuželosečky.
Viz Pech, P. Kuželosečky, str. 122-127.
-
Hlavní směry kuželosečky. Charakteristická rovnice.
ÚKOL: Řešte cvičení 7 b, c na str. 134 v Pech, P. Kuželosečky.
Viz Pech, P. Kuželosečky, str. 129-134.
-
Singulární kuželosečky.
Singulární kuželosečky jako řezy kuželové/válcové plochy rovinou
GeoGebra: Bod / GeoGebra: Dvě různoběžky / GeoGebra: Přímka / GeoGebra: Dvě rovnoběžky
Singulární bod křivky
GeoGebra: Kardioida / GeoGebra: Preclíková křivka
Singulární kuželosečka
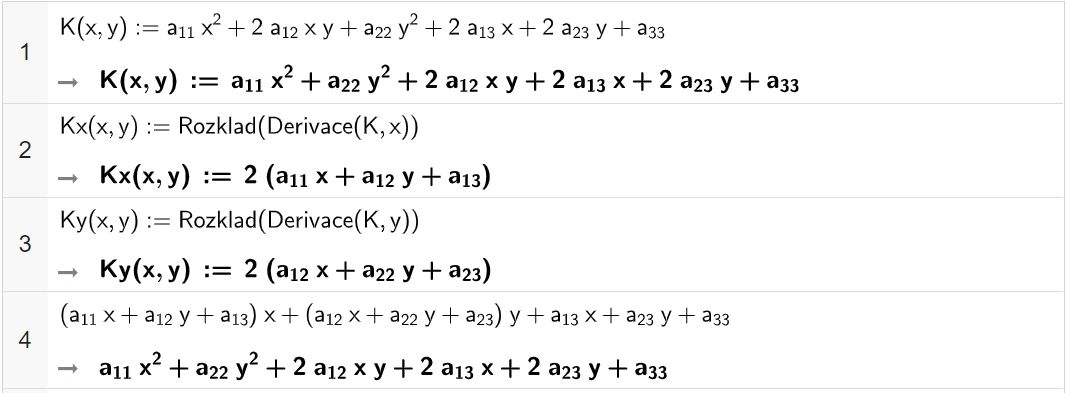
GeoGebra CASSingulární bod leží na kuželosečce a zároveň je jejím středem.
Pokud kuželosečka obsahuje kromě středu ještě nějaký další bod, je její součástí přímka.
Kuželosečka je singulární, jestliže platí $$\Delta=\left|\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{12} & a_{22} & a_{23}\\ a_{13} & a_{23} & a_{33} \end{array}\right|=0.$$ Pokud je $\Delta\neq{0}$, je kuželosečka regulární.
Hodnota $\Delta$ nás tak informuje o tom, zda je kuželosečka regulární nebo singulární, hodnota $\delta$ pak o tom, jakého je typu, tj. zda se jedná o kuželosečku eliptického, hyperbolického nebo parabolického typu.ÚKOL: Řešte cvičení 11 c, d na str. 112 v Pech, P. Kuželosečky.
-
Kvadriky
Kvadrika, též kvadratická plocha či plocha druhého stupně je přesně definována a na příkladech představena v Hašek, R., Pech, P. Kvadratické plochy a jejich reprezentace v programu Maple na str. 9-13.
Elipsoid
Hašek, R., Pech, P. Kvadratické plochy a jejich reprezentace v programu Maple na str. 67-71.
Hyperboloid
Hašek, R., Pech, P. Kvadratické plochy a jejich reprezentace v programu Maple na str. 71-81.
Paraboloid
Hašek, R., Pech, P. Kvadratické plochy a jejich reprezentace v programu Maple na str. 82-91.
Válcová plocha
Hašek, R., Pech, P. Kvadratické plochy a jejich reprezentace v programu Maple na str. 92-95.
Kuželová plocha
Hašek, R., Pech, P. Kvadratické plochy a jejich reprezentace v programu Maple na str. 95-99.
-
Elipsa jako afinní útvar ke kružnici

GeoGebra: Trojúhelníková konstrukce elipsy
Literatura
[1] Pech, P. (2004) Kuželosečky.
[2] Hašek, R., Pech, P. (2010) Kvadratické plochy a jejich reprezentace v programu Maple.
[3] Boček, L., Kočandrle, M. (2009) Analytická geometrie (Matematika pro gymnázia). Prometheus, Praha.
[4] Voráčová a kol. (2012) Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha.
[5] Budinský, B. (1983) Analytická a diferenciální geometrie. SNTL, Praha.
[6] Kuřina, F. (1996) 10 pohledů na geometrii. Praha: Akademie věd České republiky.
[7] Polák, J. (2015) Přehled středoškolské matematiky. Praha: Prometheus.
[8] Sekanina, M. a kol. (1988) Geometrie II, SPN, Praha.
Internetové odkazy
Software ke stažení
www.geogebra.org ... bezplatně dostupný program GeoGebra
wxmaxima.sourceforge.net
... bezplatně dostupný CAS program wxMaxima
Materiály pro výuku a sebevzdělávání
www.khanacademy.org/math ... Khan academy
Zkouška
Zkouška bude mít dvě části, písemnou a ústní.
V písemné části budou řešeny dva příklady vybrané z:
{[1]; str. 89/2; str. 112/11; str. 121/4, 5, 6, 8, 9, 10, 11, 12; str. 134/7; str. 141/1}.
Ústní část pak bude spočívat v zodpovězení jedné otázky vylosované z 7G2: otázky ke zkoušce.
Roman Hašek, katedra matematiky PF JU, kontakt: hasek@pf.jcu.cz