DVPP: GEOMETRIE 2 - KMA/3G2



Studijní texty ve formátu PDF

[1] Hašek, R.: Úvod do geometrie (2019)

[2] Hašek, R.: Geometrie 3 (2020)

[3] Hašek, R.: Geometrie 4 (2021)

[4] Hašek, R.: Planimetrie (2020)

[5] Pech, P. Kuželosečky (2004)

[6] Hašek, R., Pech, P. Kvadratické plochy a jejich reprezentace v programu Maple (2010)

[7] Hašek, R. Odborná matematika III (2024)


Poznámky z výuky

[P1] 3G2 20.03.2021.pdf
Projektivní rozšíření eukleidovské roviny. Homogenní souřadnice. Rovnoběžné a středové promítání. Pappova věta. Harmonická čtveřice. Kružnice a kruh, rovnice kružnice. Thaletova kružnice, Thaletova věta. Obvodový a středový úhel. Mocnost bodu ke kružnici.

[P2] 3G2 17.04.2021.pdf
Obvodový, středový a úsekový úhel, vztah mezi jejich velikostmi. Konstrukce množiny bodů, z nichž je úsečka vidět pod daným úhlem.
Řešení příkladu z otázky č. 4.



Osnova předmětu

přímá výuka (9 hod.) + distanční výuka (6 hod.)

  • Axiomatická výstavba geometrie. Eukleidovská geometrie. Eukleidovské konstrukce. Neeukleidovské geometrie.

    Geometrie vzniká z praktických důvodů (slovo geometrie pochází z řečtiny, geo- znamená "Země", -metron pak "měření"). Geometrie se zrodila v Mezopotámii (první prameny pocházejí z doby kolem 3000 př. n. l.) a v Egyptě jako umění vyměřování polí a základů staveb a určování objemů různých schránek na obchodované zboží.

    Základy geometrie jako vědy byly položeny řeckými matematiky (Thalés z Milétu, 624?-546? př. n. l.; Eukleidés, 300 př. n. l.; Archimédés, 287-212 př. n. l.). Eukleidés ve svém třináctidílném díle Základy [Eukleides, Eukleidovy základy (Elementa), překlad F. Servít, 1907.] shrnul dosavadní poznatky z matematiky a položil základy axiomatické výstavby geometrie (i celé matematiky). Při této formalizaci geometrie ale stále vycházel z nazírání reálného světa.

    Eukleidovská geometrie je založena na 5 Eukleidových postulátech, viz Úvod do geometrie (2019), str. 11. Pátý z nich sehrál výraznou roli ve vývoji geometrie, konkrétně v 19. století při "objevení" tzv. neeukleidovských geometrií (Lobačevského geometrie, Riemannova geometrie). Revizi axiomatické výstavby geometrie vedoucí k její vyšší formalizaci provedl David Hilbert.

    Zdroje: Úvod do geometrie (2019) (str. 4-11). Geometrie 3 (2020), (str. 96-106).

    GeoGebra: [Eukleidovské konstrukce]

    Příklad:  Užitím pouze pravítka bez měřítka a kružnice rozdělte danou úsečku AB na tři stejné části.

    Otázka č. 1: [1] str. 10-12; [2] str. 96-109; [7] str. 7-30

  • Projektivní rozšíření eukleidovského prostoru. Projektivní geometrie.

    Nevlastní body. Projektivní rozšíření eukleidovského prostoru. Homogenní souřadnice. Princip duality. Dvojpoměr. Harmonická čtveřice. Pappova věta.

    Zdroje: Geometrie 4 (2021), (str. 14-32).

    Příklad:  Rovnici kuželosečky přepište do homogenních souřadnic a určete její nevlastní body: -x2+ 2xy+ 3y2-2x+ 4y+ 1 = 0.

    [Kuželosečka v GeoGebře]

    Otázka č. 2: [3] str. 14-30; [7] str. 41-60

  • Kružnice.
    Definice (řez na kuželové ploše, množina bodů dané vlastnosti). Rovnice. Kruh.
    • Thaletova kružnice. Obvodový a středový úhel kružnice.
    • Mocnost bodu ke kružnici.
    • Kruhová inverze.

    Zdroje: Hašek, R.: Úvod do geometrie (2019), (str. 10). Planimetrie (2020), (str. 129-136). Geometrie 4 (2021), (str. 8-13).

    Příklad:  Sestrojte kružnici k, která prochází danými různými body A, B a dotýká se dané přímky t.

    [Řešení I: mocnosti bodu ke kružnici a pomocná kružnice] [Řešení II: mocnosti bodu ke kružnici a Eukleidova věta o odvěsně]

    Příklad:  Sestrojte kružnici procházející danými body A, B a dotýkající se dané kružnice k; body A, B jsou vnější body kružnice k.

    [Řešení: kruhová inverze; převedení na předchozí případ bod-bod-přímka]

    Otázka č. 3: [1] str. 26, 51; [4] 129-136; Wikipedia: Circle

    Úsekový úhel

    Úsekový úhel příslušný k oblouku AB kružnice, viz obrázek, je úhel, jehož jedním ramenem je polopřímka AB a druhým ramenem je polopřímka AX, kde X je bod tečny ke kružnici v bodě A volený tak, aby oblouk AB byl částí úhlu BAX. (Terminologická komise JČMF. (1981) Slovník školské matematiky. Praha: Státní pedagogické nakladatelství.)

    Úsekový úhel

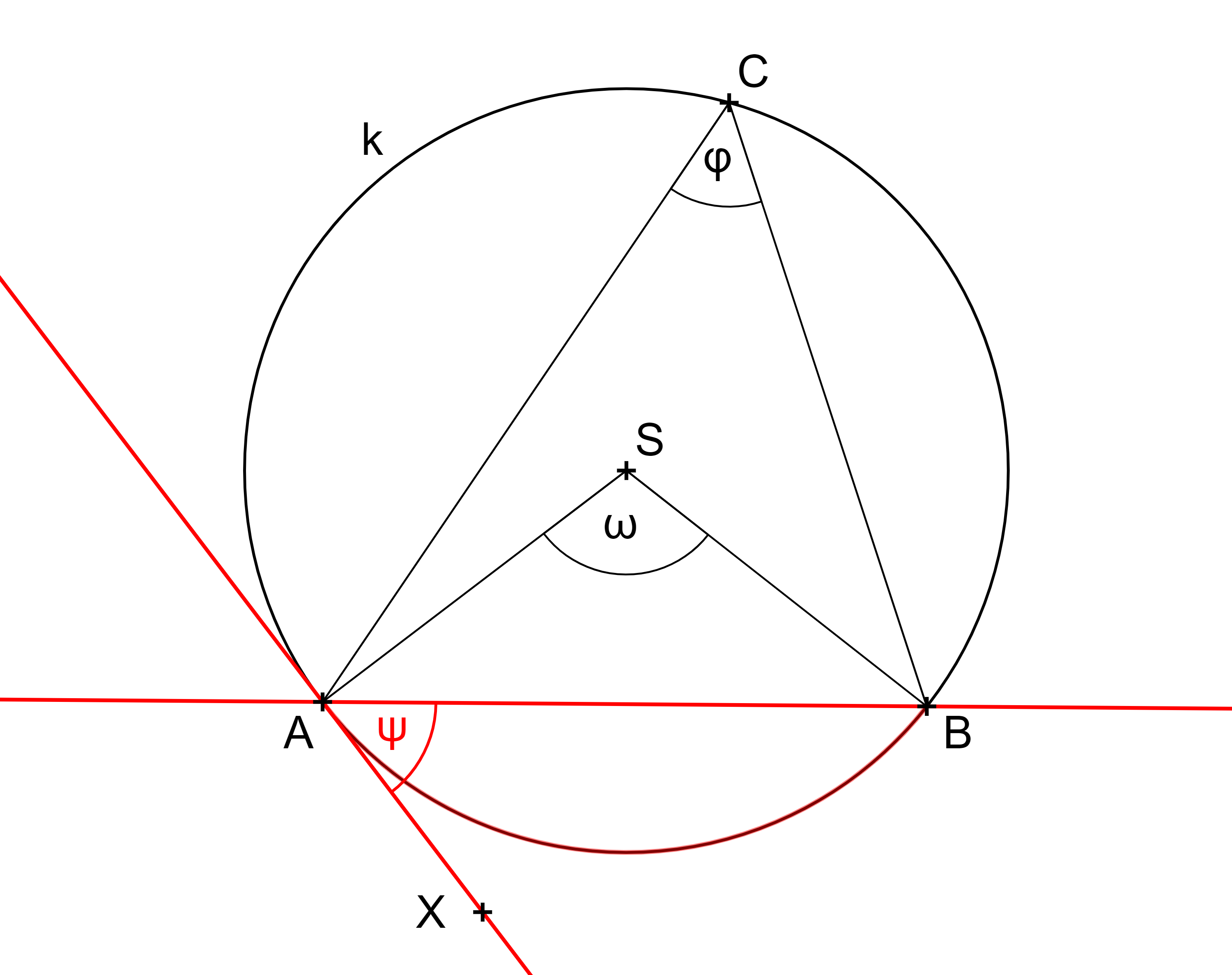
    Vztah mezi velikostí obvodového a středového úhlu: Velikost obvodového úhlu příslušejícího oblouku AB je rovna polovině velikosti středového úhlu příslušejícího témuž oblouku. [GeoGebra aplet]

    Otázka č. 4: [1] str. 10, 26, 51; Wikipedia: Circle

  • Elipsa.
    Definice (řez na kuželové ploše, množina bodů dané vlastnosti). Rovnice, kanonický tvar rovnice. Tečna elipsy. Řídící a vrcholová kružnice elipsy. Sdružené průmery. Bodová konstrukce. Trojúhelníková konstrukce. Rytzova konstrukce. Proužková konstrukce. Oskulační kružnice. Aplikace.

    GeoGebra: [Řez kuželové plochy rovinou]

    Quételetova-Dandelinova věta pro kuželovou plochu:  Rovina, která naní vrcholová, ani není kolmá k ose a která s rovinou povrchové kružnice rotační kuželové plochy svírá úhel menší než povrchové přímky plochy, protíná rotační kuželovou plochu v elipse. Jejími ohnisky jsou dotykové body kulových ploch, které jsou vepsány kuželové ploše a dotýkají se roviny řezu ([1], str. 208).

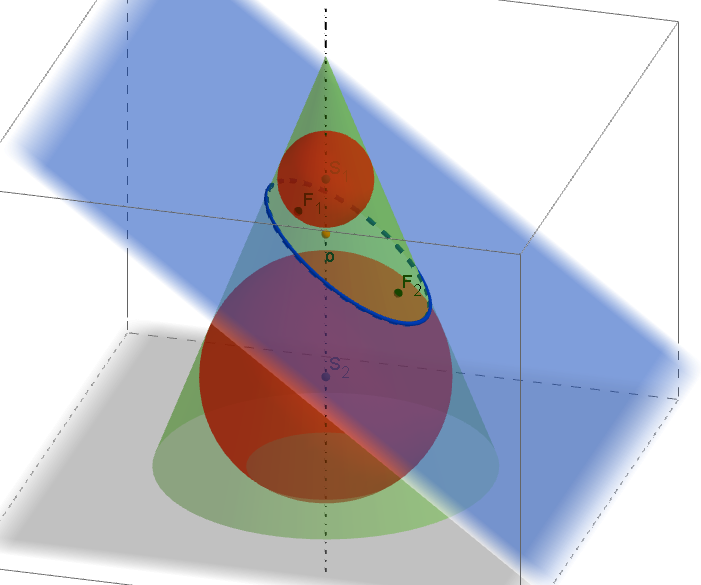
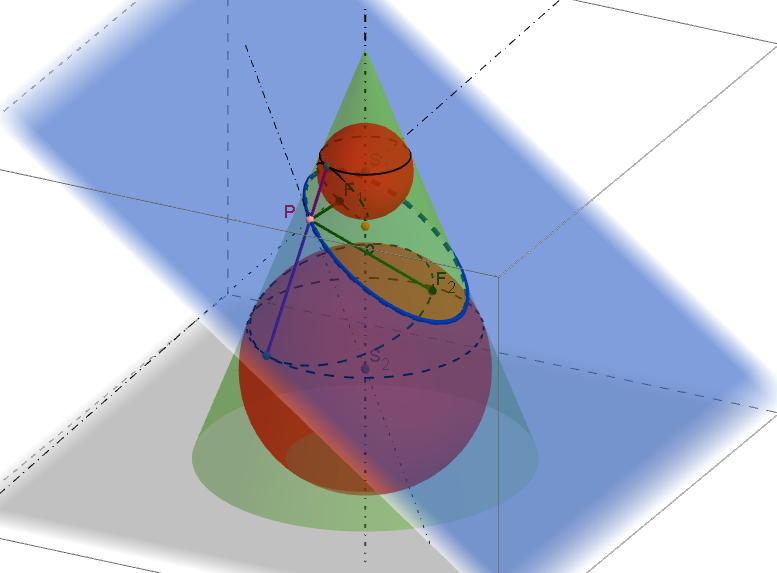
    Quételetova-Dandelinova věta pro kuželovou plochu             Quételetova-Dandelinova věta pro kuželovou plochu

    Quételetova-Dandelinova věta pro kuželovou plochu a její důkaz

    GeoGebra: [Elipsa - definice] [Elipsa - konstrukce (F1, F2, a)]

    Zdroje: Kuželosečky (2004), (str. 7-25).

    Otázka č. 5: [5] str. 56, 7-25

    Otázka č. 7: [5] str. 7-25

  • Hyperbola.
    Definice (řez na kuželové ploše, množina bodů dané vlastnosti). Rovnice. Konstrukce. Fokální vlastnosti. Aplikace.

    GeoGebra: [Hyperbole - definice]

    Zdroje: Kuželosečky (2004), (str. 26-43).

    Otázka č. 6: [5] str. 56, 26-31

    Otázka č. 8: [5] str. 26-31

  • Parabola.
    Definice (řez na kuželové ploše, množina bodů dané vlastnosti). Rovnice. Konstrukce. Fokální vlastnosti. Aplikace.

    Zdroje: Kuželosečky (2004), (str. 44-55).

    Otázka č. 9: [5] str. 56, 44-52

    Otázka č. 10: [5] str. 75-76, 93, 101, 115, 116-119, 122-126,129

  • Kvadratické plochy

    GeoGebra: [Chladicí věž]

    Zdroje: Kvadratické plochy a jejich reprezentace v programu Maple (2010), (str. 67-99).

    Otázka č. 11: [6] str. 67-100

  • Kruhová inverze

    Příklad:  Jsou dány tři kružnice k1, k2, k3, z nichž se každé dvě zvenku dotýkají. Sestrojte kružnici k, dotýkající se daných kružnic.

    [Řešení v GeoGebře]

    Otázka č. 12: [3] str. 8-13



Další studijní literatura

[1] Eukleides, Eukleidovy základy (Elementa), překlad F. Servít, 1907.
Dostupné na https://commons.wikimedia.org/wiki/File:Eukleides_Servit.pdf
[2] Kuřina, F.: 10 geometrických transformací. Prometheus, Praha, 2002.
[3] Kuřina, F.: 10 pohledů na geometrii. Akademie věd České republiky, 1996.
[4] Voráčová a kol., Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha, 2012.



Doplňková studijní literatura

-  Sekanina, M. a kol.: Geometrie II, SPN, Praha 1988.
-  Budinský, B.: Analytická a diferenciální geometrie. SNTL, Praha, 1983.
-  Kuřina, F.: 10 pohledů na geomatrii. Akademie věd České republiky, 1996.
-  Voráčová a kol., Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha, 2012.



Internetové odkazy

Software ke stažení

www.geogebra.org ... program GeoGebra (možnost bezplatného stažení)

Materiály pro výuku a sebevzdělávání

i2geo.net ... portál pro sdílení výukových materiálů dynamické geometrie
wiki.geogebra.org ... GeoGebra Wiki - manuál, výukové materiály, fórum apod.
wiki.geogebra.org/cs/ ... postupně překládaná česká verze GeoGebra Wiki
www.youtube.com/user/GeoGebraChannel ... GeoGebra na YouTube
www.geogebratube.org ... Materiály v GeoGebře ke stáhnutí
www.cut-the-knot.org ... Interactive Mathematics Miscellany and Puzzles
http://www.math.uoc.gr ... Geometrikon - galerie geometrických témat



Požadavky na studenta

|Úvod|

Roman Hašek, katedra matematiky PF JU, kontakt: hasek@pf.jcu.cz