PLANIMETRIE - KMA/PLA

Předmět Planimetrie je věnován detailnímu seznámení s afinními transformacemi roviny, především se shodnostmi a podobnostmi, a s jejich použitím v konstrukčních úlohách.

Kompletní učební text ve formátu PDF: Hašek: PLANIMETRIE - KMA/PLA (aktualizováno 9. 4. 2018).

Kompletní učební text ve formátu PDF: Hašek: PLANIMETRIE - KMA/PLA (aktualizováno 19. 5. 2020).

Osnova předmětu

• Afinní zobrazení. Afinní transformace roviny.

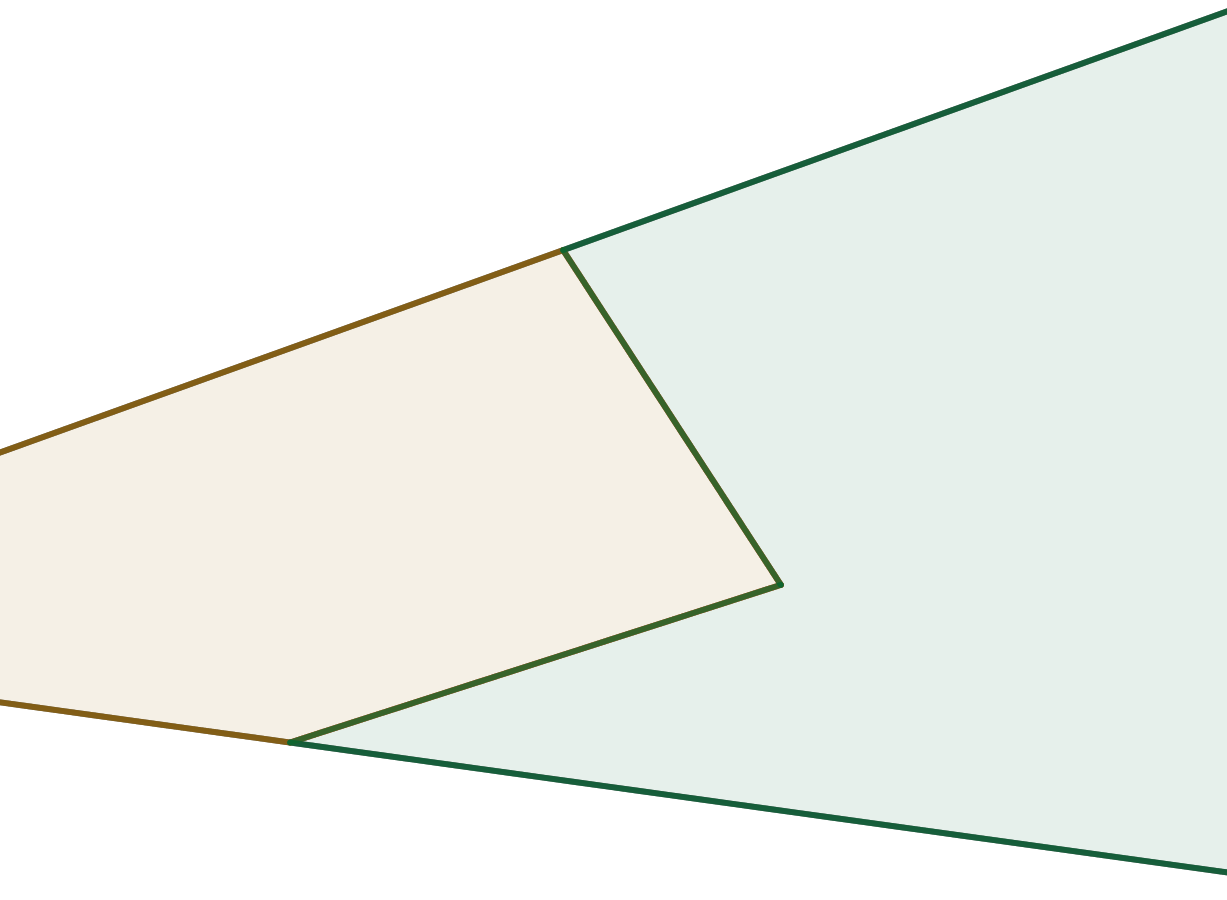
  PŘEDNÁŠKA 1 Úvod. Vybrané pojmy, které budeme dále používat. Geometrická zobrazení. GeoGebra: [Rovnoběžné promítání] [Středové promítání] Příklad 1:  Pomocí programu GeoGebra vyzkoumejte, zda se v následujících zobrazeních zobrazí střed úsečky zase na střed úsečky: stejnolehlost, osová afinita, středová kolineace, kruhová inverze. Využijte aplety s ukázkami uvedených zobrazení: [Stejnolehlost] [Osová afinita] [Středová kolineace] [Kruhová inverze] Prémiový úkol č. 1: Na obrázku jsou znázorněny hranice dvou pozemků. Jejich společná hranice je tvořena lomenou čarou. Nahraďte jí úsečkou tak, aby výměra zahrad zůstala zachována. (Podmínky řešení prémiových příkladů viz Požadavky)

  CVIČENÍ 1 (Geometrické zobrazení) Zaregistrujte se na stránce geogebra.org. Vstupte do skupiny PLA 2020! Příklad 1: Sestrojte libovolný trojúhelník ABC a jeho střední příčky. Věta o středních příčkách trojúhelníku říká, že střední příčka trojúhelníku je rovnoběžná s protilehlou stranou a její délka je vzhledem k této straně poloviční. Pokuste se tuto větu dokázat. Jaký je vztah mezi trojúhelníky, které na obrázku vidíme? Varignonova věta: Středy stran libovolného čtyřúhelníku tvoří rovnoběžník. 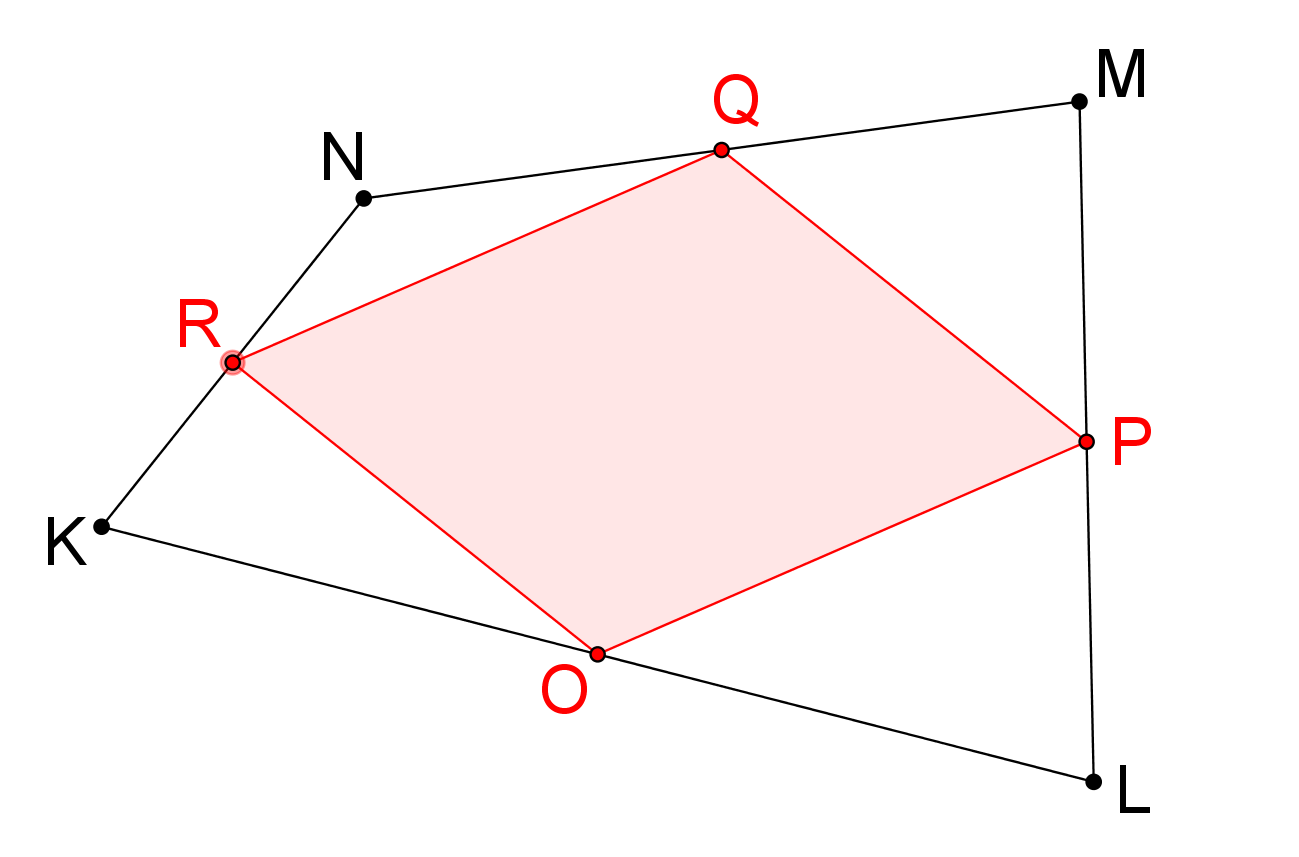(Pierre Varignon, 1654-1722) Domácí úkol č. 1: Užitím programu GeoGebra sestrojte libovolný čtyřúhelník KLMN a středy jeho stran O, P, Q, R. Ověřte pravdivost tvrzení Varignonovy věty a pokuste se ji dokázat. Potom vyslovte hypotézu o vztahu obsahů čtyřúhelníku KLMN a rovnoběžníku OPQR. Tuto hypotézu také dokažte. Řešení úkolu vložte do skupiny PLA 2020.

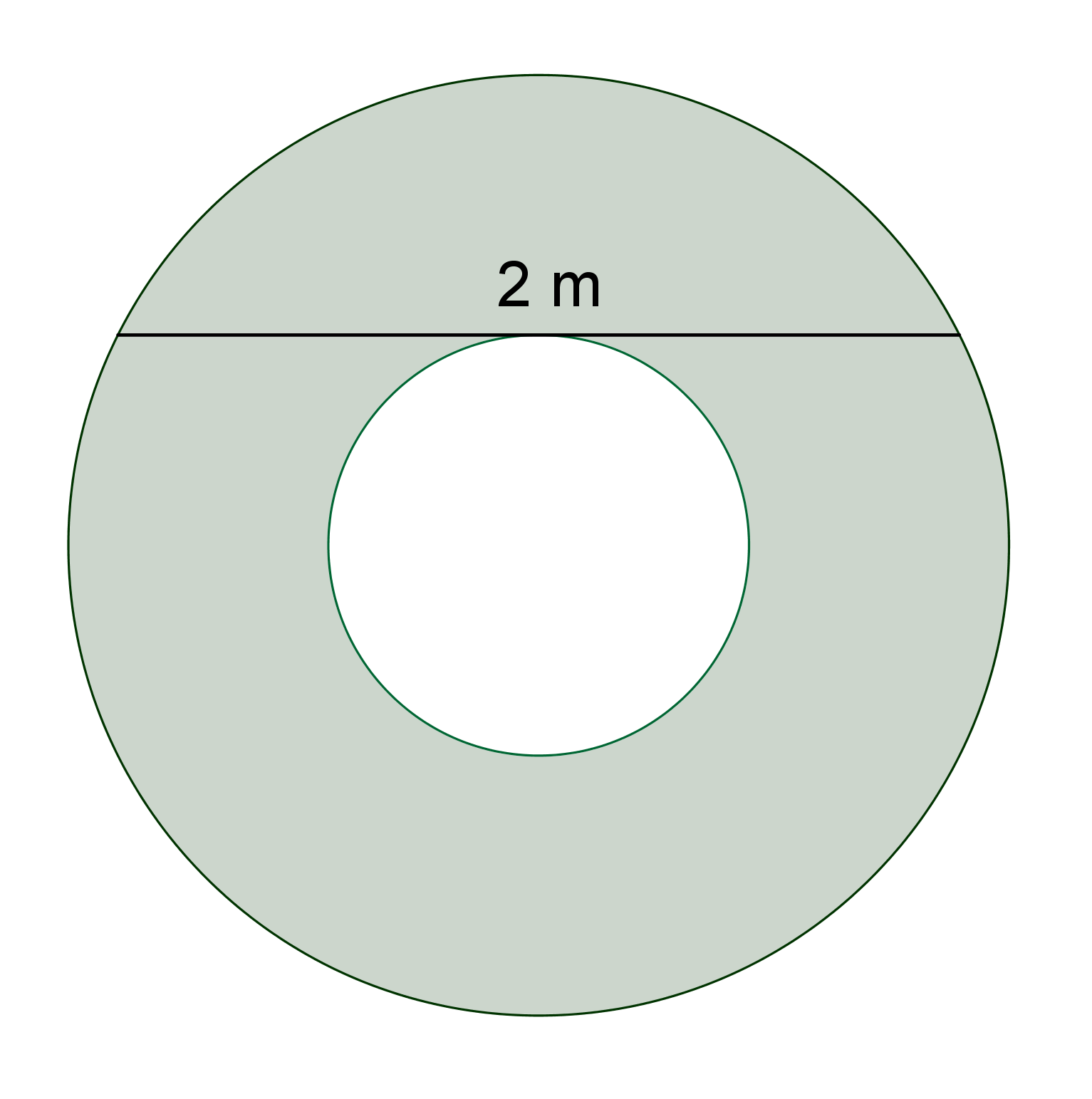
  PŘEDNÁŠKA 2 Afinní zobrazení. Dělicí poměr. Příklad 1: Určete dělicí poměr (ABS) středu S úsečky AB vzhledem k jejím krajním bodům A, B. Prémiový úkol č. 2:  Určete velikost vybarveného mezikruží, je-li délka tětivy tečné k jeho vnitřní hraniční kružnici 2 m, viz obrázek.

  CVIČENÍ 2 (Dělicí poměr) Příklad 1: Přímka p je dána body A a B. Jaký je rozdíl v tom, když určíme polohu bodu C na této přímce a) jeho vzdálenostmi od bodů A, B, b) poměrem jeho vzdáleností od bodů A, B. Příklad 2: V rovině jsou dány dva pevné body A a B. Určete množinu všech bodů X této roviny, pro které platí |AX|/|BX|=k, kde k je reálná konstanta. Použijte program GeoGebra, modelujte v něm zadání, pokuste se vykreslit příslušnou křivku a určit její rovnici. [Řešení v GeoGebře] Domácí úkol č. 2: Na volný papír narýsujte trojúhelník ABC, sestrojte jeho výšky a jejich průsečík označte O (ortocentrum). Potom postupně zobrazte bod O v osových souměrostech s osami AB, BC a CA. Vyslovte hypotézu o polohách těchto bodů. Řešení úkolu vyfoťte nebo oskenujte a vložte do skupiny PLA 2020.

• Shodná zobrazení v rovině. Analytické vyjádření shodností.

  PŘEDNÁŠKA 3 Afinní transformace roviny - Afinita. [Afinní transformace roviny: "Úprava" fotografie] Příklad 1: V programu GeoGebra sestrojte přímku danou body A a B a libovolně na ní umístěte bod C. Potom tažením myší měňte polohy bodů A, B a sledujte chování bodu C. Co pro něj platí? Své tvrzení podložte výpočtem provedeným v programu. Příklad 2: Pro body A, B, C platí (ABC)=λ. Zapište pomocí λ dělicí poměr (CBA). Domácí úkol č. 2: (Pokračování příkladu 2.) Pro body A, B, C platí (ABC)=λ. Zapište pomocí λ dělicí poměry (BAC), (ACB), (CAB) a (BCA). Domácí úkol č. 3: Pomocí appletu "Úprava" fotografie zapište maticové rovnice následujících zobrazení: (i) osová souměrnost podle osy y, (ii) středová souměrnost podle počátku, (iii) středová souměrnost se středem v bodě [0,5]. 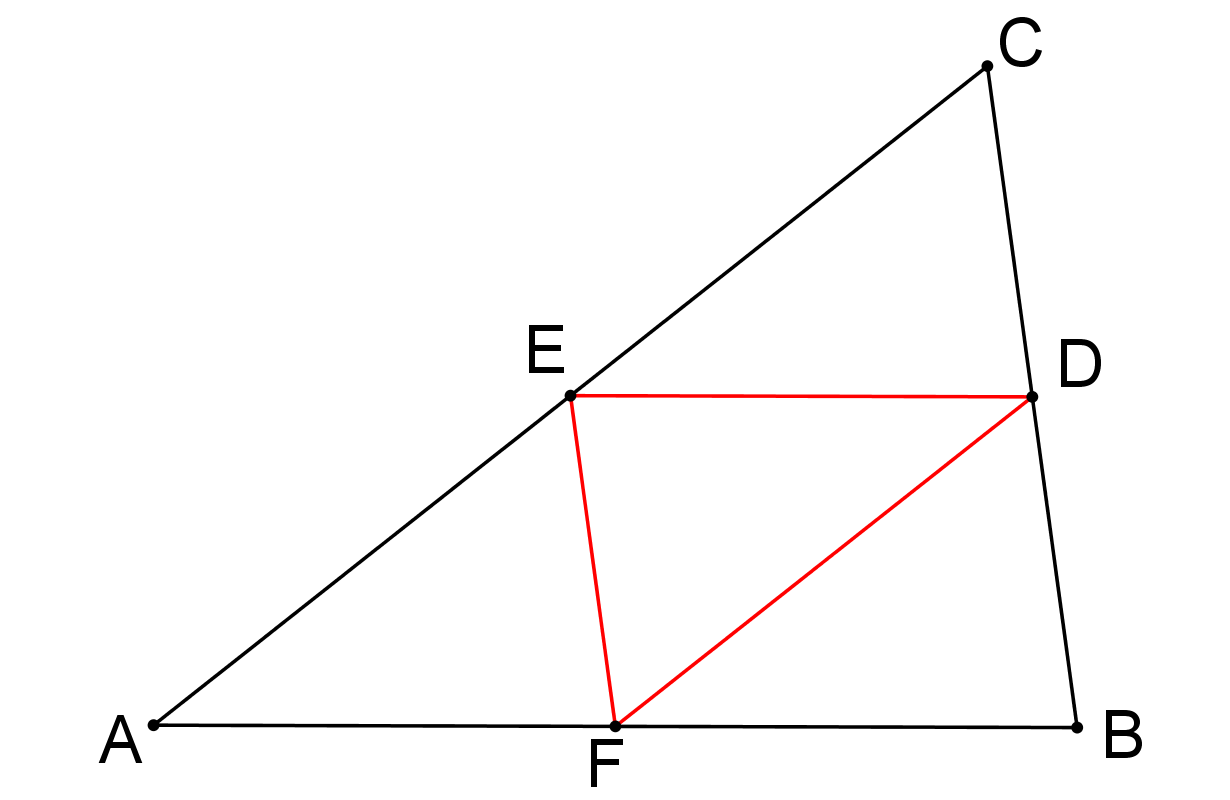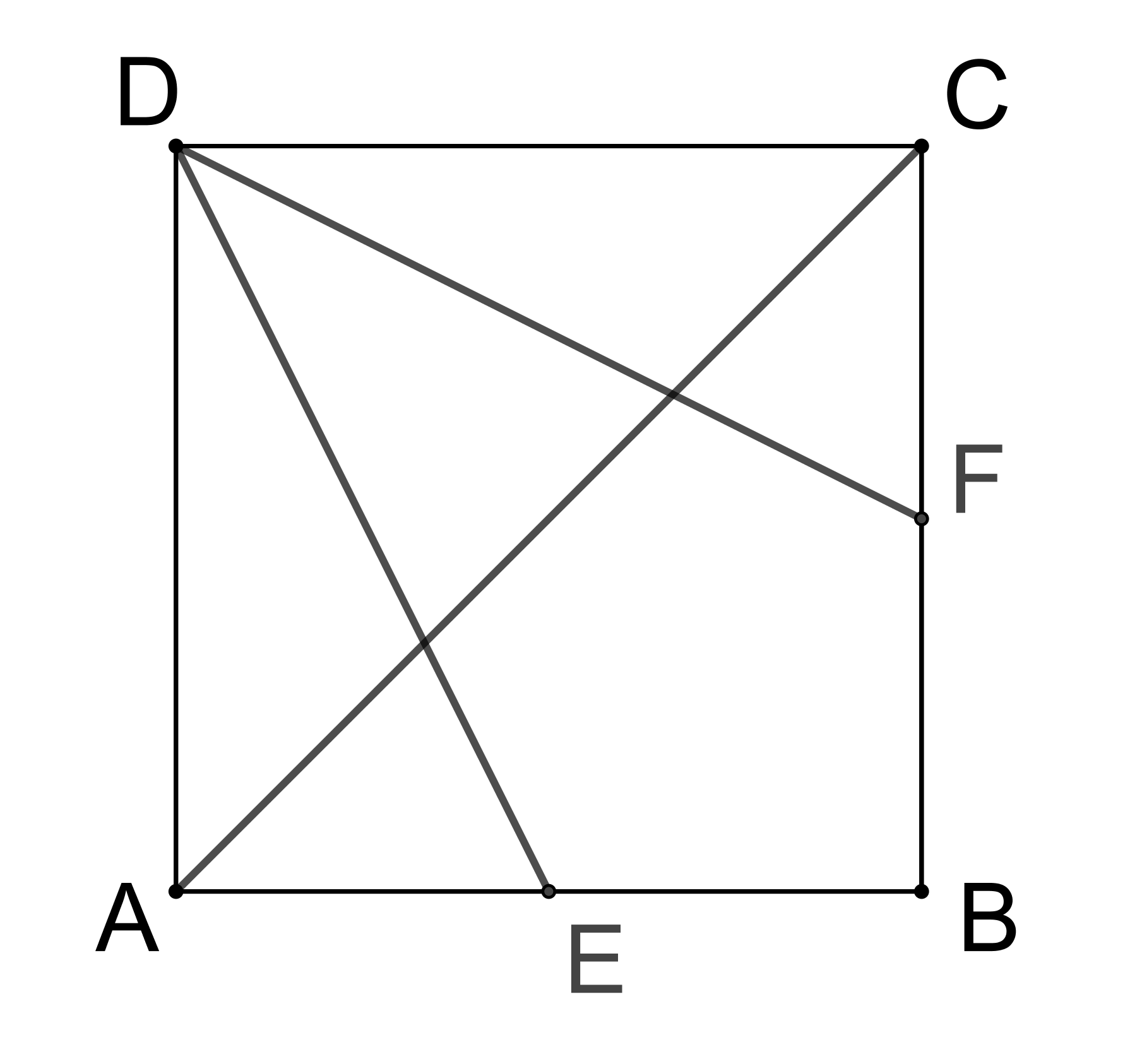Prémiový úkol č. 3: Úhlopříčka AC čtverce ABCD je rozdělena na tři části dvěma příčkami, které spojují vrchol D se středy E a F stran AB a BC, viz obrázek. Rozhodněte, zda jsou uvedené tři části úhlopříčky AC stejně dlouhé. Pravdivost svého tvrzení dokažte!

• Osová souměrnost.

  CVIČENÍ 3 (Osová souměrnost) Vztah mezi velikostí obvodového a středového úhlu: Velikost obvodového úhlu příslušejícího oblouku AB je rovna polovině velikosti středového úhlu příslušejícího témuž oblouku. [GeoGebra aplet] Tětivový čtyřúhelník: Čtyřúhelník vepsaný do kružnice, součet jeho protilehlých úhlů je 180° (viz Wikipedia: Cyclic quadrilateral).

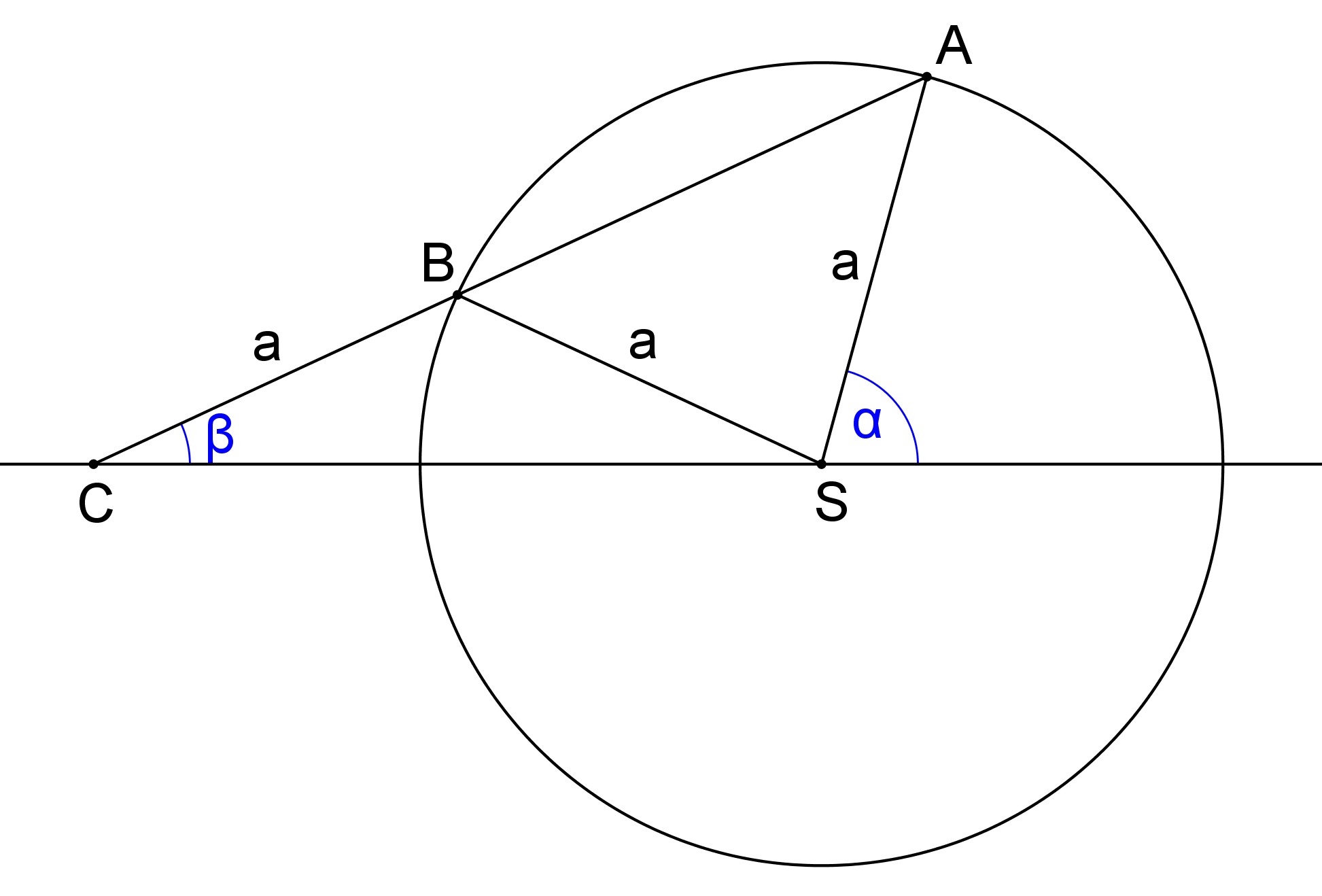
  PŘEDNÁŠKA 4 Afinní transformace roviny - Afinita. [Afinní transformace roviny: "Úprava" fotografie] Prémiový úkol č. 4:  Jaký je vzah mezi velikostmi úhlů α a β? Své tvrzení dokažte!

  CVIČENÍ 4 (Osová souměrnost) Příklad 1: Je dána přímka p a body A, B v téže polorovině s hraniční přímkou p. Najděte všechny body X ∈ p takové, že součet vzdáleností |AX|+|BX| je minimální. (Tato úloha je známa jako Heronův problém; Hérón Alexandrijský, přibl. 10-70 n.l.) Vivianiho věta: Součet vzdáleností libovolného bodu v rovnostranném trojúhelníku od jeho stran je roven výšce tohoto trojúhelníku. [en.wikipedia.org: Viviani's theorem] [Dynamický důkaz]

  5. týden / 16.-22. 3. / Samostudium: Shodná zobrazení v rovině Zde je zadání samostatné práce pro 5. týden: Prostudujte prosím následující text "Shodná zobrazení v rovině - analytické vyjádření, samodružné body a směry" (navazuje na texty zveřejněné výše) a co nejlépe vyřešte Příklady 5.1 až 5.9, které jsou v textu uvedeny. K zaznamenání Vašeho postupu při jejich řešení použijte prostředky dle vlastní úvahy, papír a tužku, GeoGebru a textový editor nebo jakýkoliv jiný vhodný software. Řešení zatím nikam neposílejte. V dohledné době bych rád spustil naší komunikaci prostřednictvím aplikace Microsoft Teams (https://helpdesk.jcu.cz). Budu Vás o všem informovat. V případě dotazů k obsahu výše uvedeného textu a k postupu řešení příkladů použijte v mezičase e-mail. 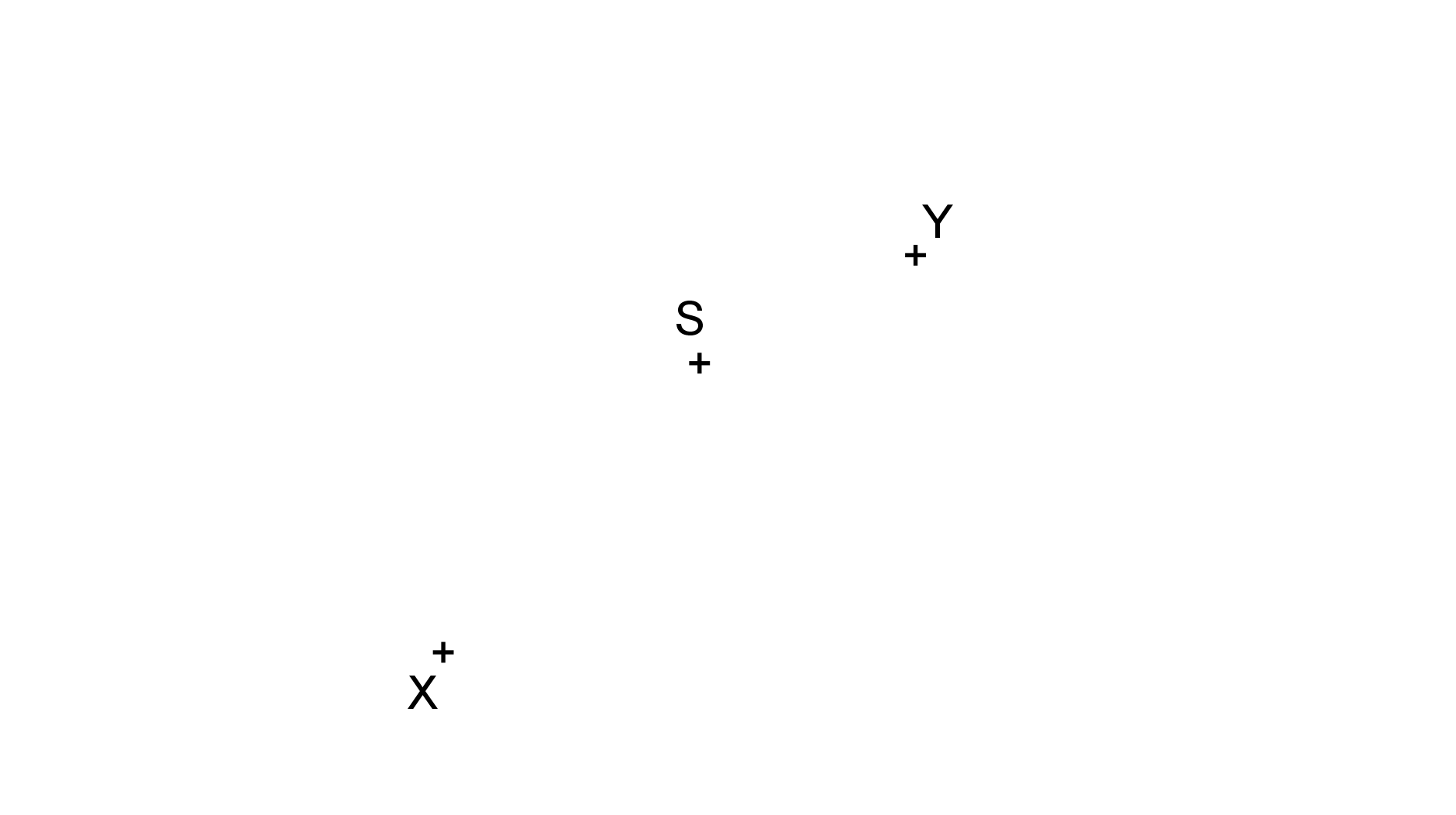Prémiový úkol č. 5:  Jsou dány body X, Y a S, viz obrázek. Sestrojte čtverec ABCD tak, aby bod X ležel na přímce AB, bod Y na přímce BC a bod S byl středem čtverce. 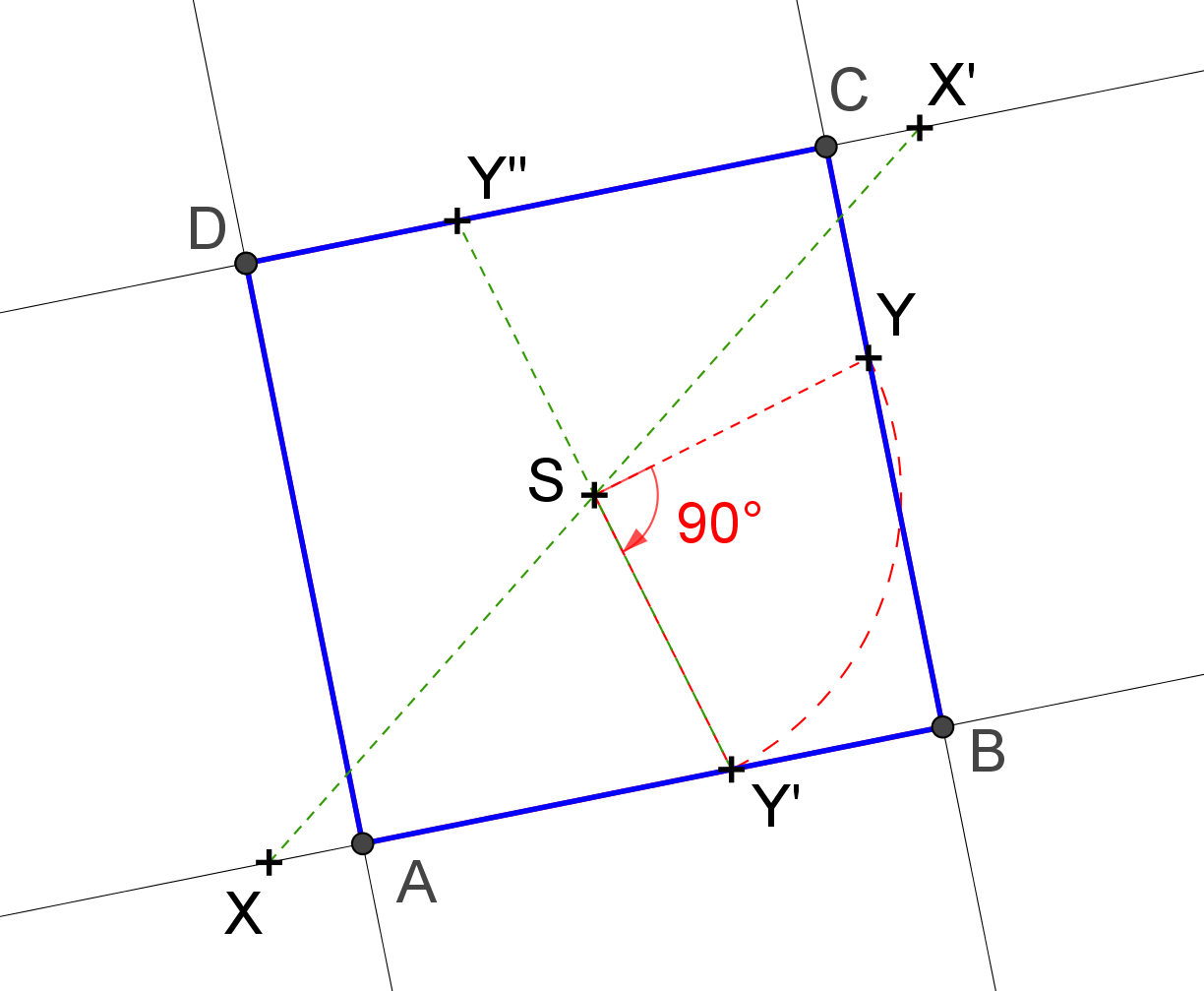Prémiový úkol č. 5 - Řešení: Postupujeme dle obrázku. Nejprve zobrazíme bod Y v otočení se středem S o úhel -90°. Výsledný bod Y', spolu s X potom zobrazíme ve středové souměrnosti se středem S. Dostaneme body Y'' a X'. Pak už máme dost bodů, abychom sestrojili celý čtverec. Upozorňuji, že toto není jediný postup. Například ti, kteří poslali svá řešení, používali různé jiné postupy, vždy však založené na principu zobrazení jedné strany čtverce na jeho jinou stranu, sousední nebo protilehlou.

  6. týden / 23.-27. 3. / Samostudium: Výpočet samodružných bodů a směrů shodností v rovině Především Vás informuji, že jsem podstatně rozšířil text z minulého týdne, přidal jsem řešení nebo návody k řešení u vybraných příkladů. Zde je nová, rozšířená, verze textu:"Shodná zobrazení v rovině - analytické vyjádření, samodružné body a směry (rozšířená verze)". Stále platí, že máte řešit příklady z tohoto textu: 5.1 až 5.4 kompletně; 5.5 dokončit, co jem neudělal já; 5.6, 5.7 a 5.9 kompletně; 5.8 jsem udělal já. Zde je zadání samostatné práce pro 6. týden: Prostudujte prosím následující text "Shodná zobrazení v rovině - výpočet samodružných bodů a směrů" a co nejlépe vyřešte Příklad 5.10. K zaznamenání Vašeho postupu při jejich řešení použijte prostředky dle vlastní úvahy, papír a tužku, GeoGebru a textový editor nebo jakýkoliv jiný vhodný software. Řešení pošlete v rámci týmu v aplikaci Teams. V případě dotazů použijte prostředí Teams nebo e-mail. 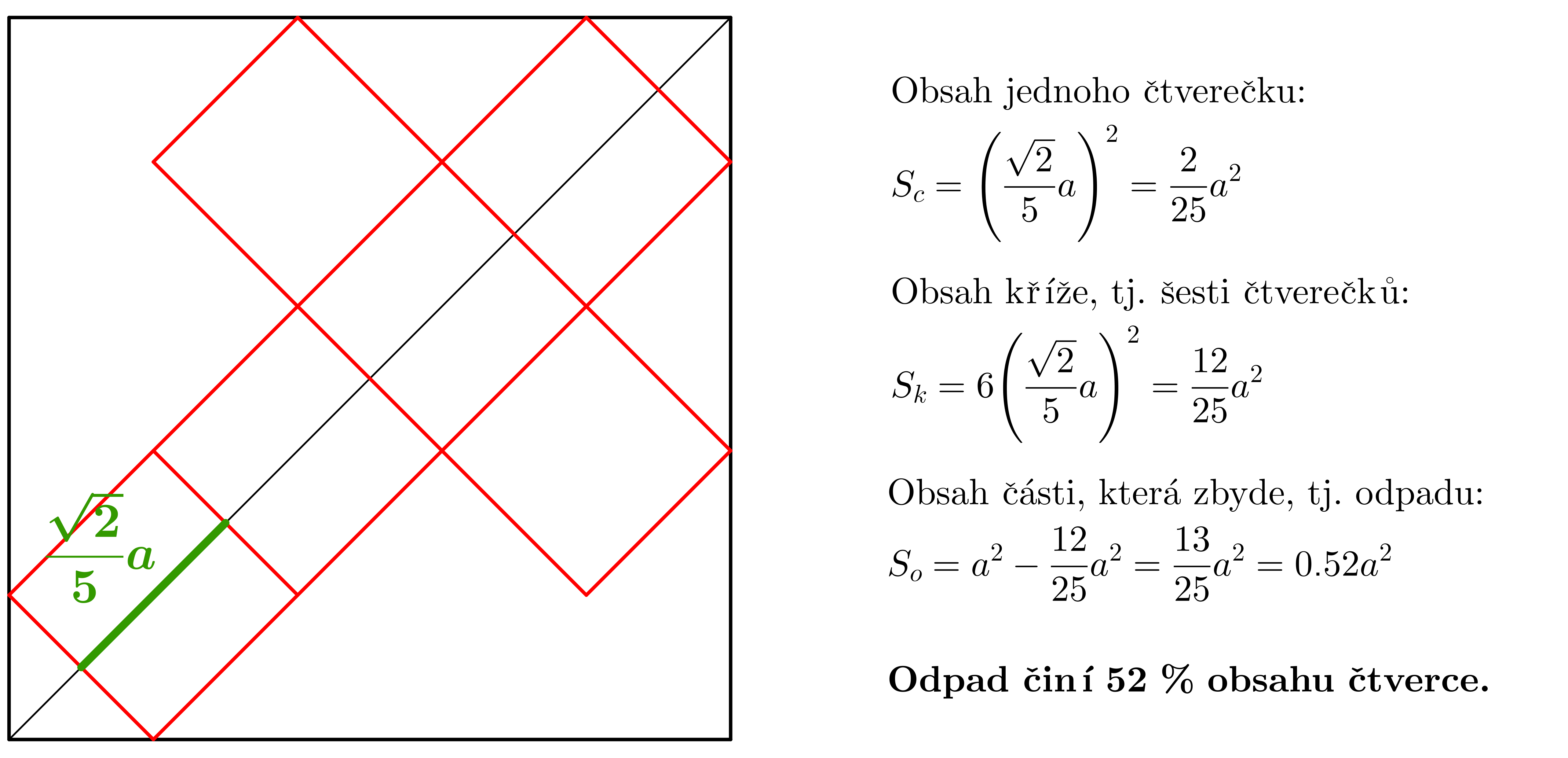Užitečné odkazy: wxMaxima (download) Program wxMaxima ve výuce matematiky (článek) Afinní transformace roviny - zobrazení úsečky (GeoGebra applet) Prémiový úkol č. 6:  Ze čtverce byl vystřižen kříž tvořící síť krychle, viz obrázek. Určete procento odpadu! 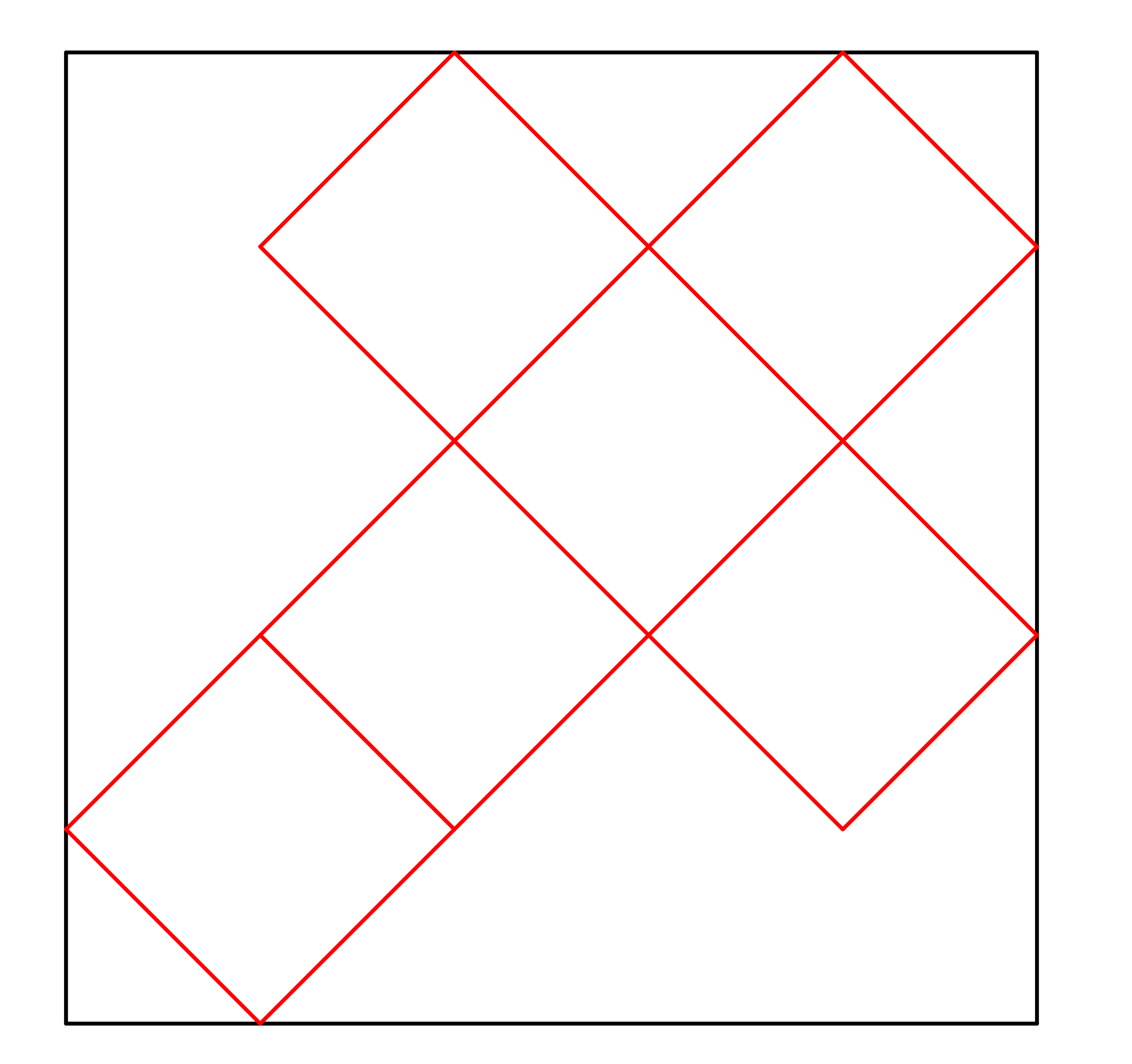Prémiový úkol č. 6 - Řešení:

  7. týden / 30. 3.-3. 4. / Samostudium: Symetrie. Osová souměrnost. Zde je zadání samostatné práce pro 7. týden: Prostudujte prosím následující text "Shodná zobrazení v rovině - Symetrie. Osová souměrnost." a co nejlépe vyřešte příklady a cvičení vysazené modrou barvou. K zaznamenání Vašeho postupu při jejich řešení použijte prostředky dle vlastní úvahy, papír a tužku, GeoGebru a textový editor nebo jakýkoliv jiný vhodný software. Konstrukční úlohy můžete řešit v GeoGebře, vždy však k nim udělejte i rozbor, ručně, tužkou na papír. Řešení pošlete v rámci týmu v aplikaci Teams. V případě nejasností se ptejte, použijte prostředí Teams nebo e-mail. Užitečné odkazy: Symmetry in Geometry (video) GeoGebra: Návody Introduction to GeoGebra (webinar-video) Prémiový úkol č. 7:  Určete délku strany největšího čtverce, který lze vepsat do jednotkové krychle. Jinak řečeno, jaký největší pevný čtverec můžete vložit do krychlové krabice o délce hrany 1 m? Prémiový úkol č. 7 - Řešení: Vyřešení daného problému je klíčovým krokem při řešení otázky známé jako problém krychle prince Ruperta, viz Prince Rupert's cube: Jakou největší krychli můžeme protáhnot otvorem vytvořeným v jednotkové krychli?. Námi hledaný čtverec je obrysem tohoto otvoru. Délka jeho strany je 3√2/4≈1,06. Více viz Wikipedia: Prince Rupert's cube nebo WolframMathWorld: Prince Rupert's Cube, případně The cube shadow theorem (pt.1): Prince Rupert's paradox (video).

  8. týden / 6. 4.-10. 4. / Samostudium: Středová souměrnost. Otočení. Zde je zadání samostatné práce pro 8. týden: Prostudujte prosím následující text "Středová souměrnost. Otočení." a co nejlépe vyřešte příklady a cvičení vysazené modrou barvou (Upozorňuji, že text jsem 15. 4. vyměnil! V původním textu jsem při kontrolním čtení objevil závažnou chybu - v pojednání o orientovan0m úhlu jsem prohodil "proti" a "ve" směru pohybu hodinových ručiček, čímž došlo k zásadní změně smyslu celé příslušné věty. Za to se omlouvám!). K zaznamenání Vašeho postupu při jejich řešení použijte prostředky dle vlastní úvahy, papír a tužku, GeoGebru a textový editor nebo jakýkoliv jiný vhodný software. Konstrukční úlohy můžete řešit v GeoGebře, vždy však k nim udělejte i rozbor, ručně, tužkou na papír. Rozbor udělejte, i když nevíte, jak úlohu řešit! Řešení pošlete v rámci týmu v aplikaci Teams. V případě nejasností se ptejte, použijte prostředí Teams nebo e-mail. Užitečné odkazy: Rotations on a Coordinate Plane (Tarver Academy Math) (video) Rotating Points Using Rotation Matrices (video) How to translate a triangle using a transformation vector (video) Transformations - Translating A Triangle On The Coordinate Plane (video) GeoGebra: Návody Introduction to GeoGebra (webinar-video) Prémiový úkol č. 8:  V trojúhelníku ABC je S průsečíkem os stran (tj. střed kružnice opsané) a O průsečíkem výšek (tj. ortocentrum), viz obrázek. Dokažte, že součet vektorů SA, SB, SC je roven SO, tj. SA+SB+SC=SO. 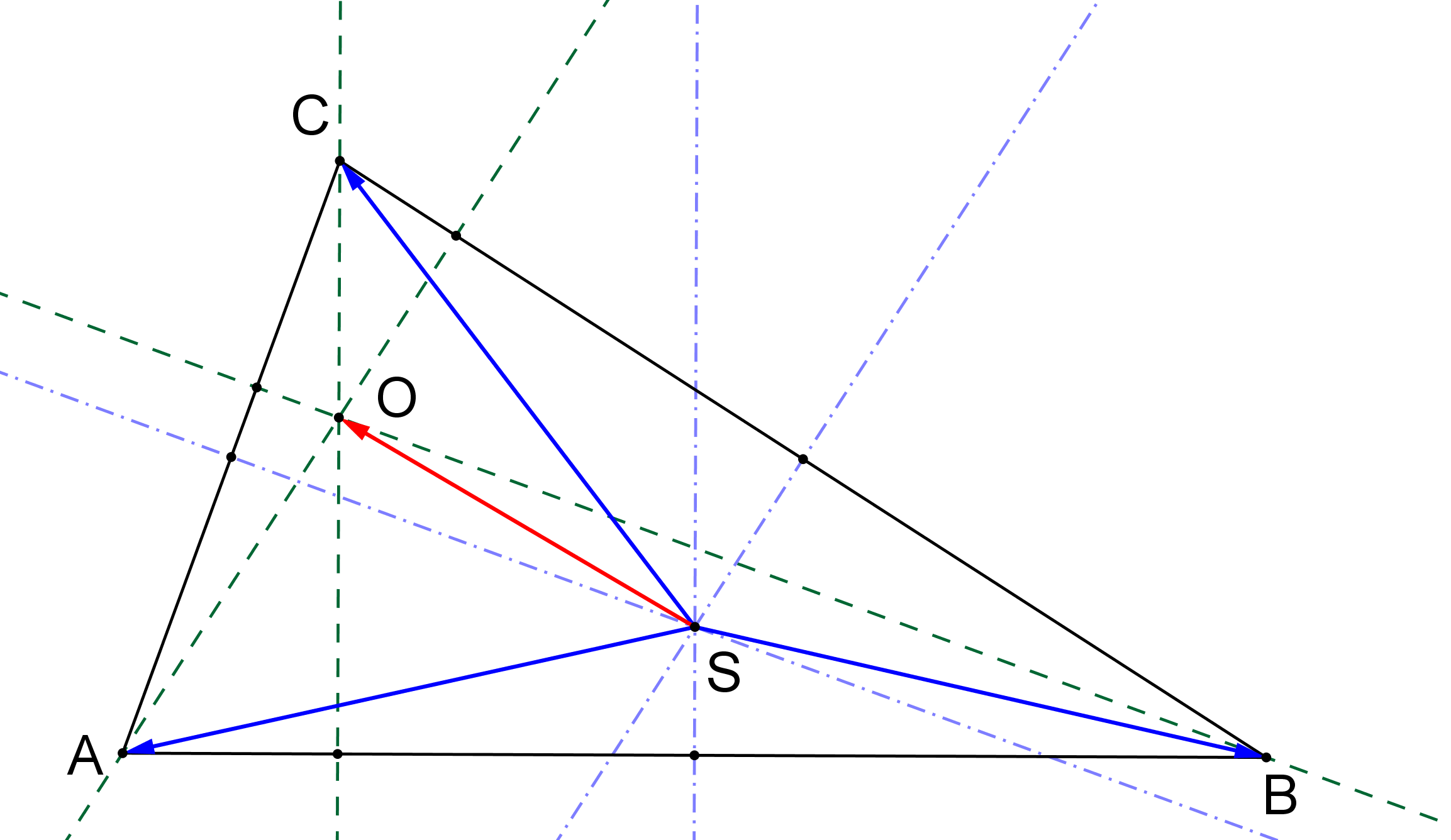Prémiový úkol č. 8 - Nápověda: Termín pro odevzdání úplného řešení přesouvám na pátek 17. 4. 23:59 hodin. Zatím zde uvádím 1. nápovědu, viz obrázek.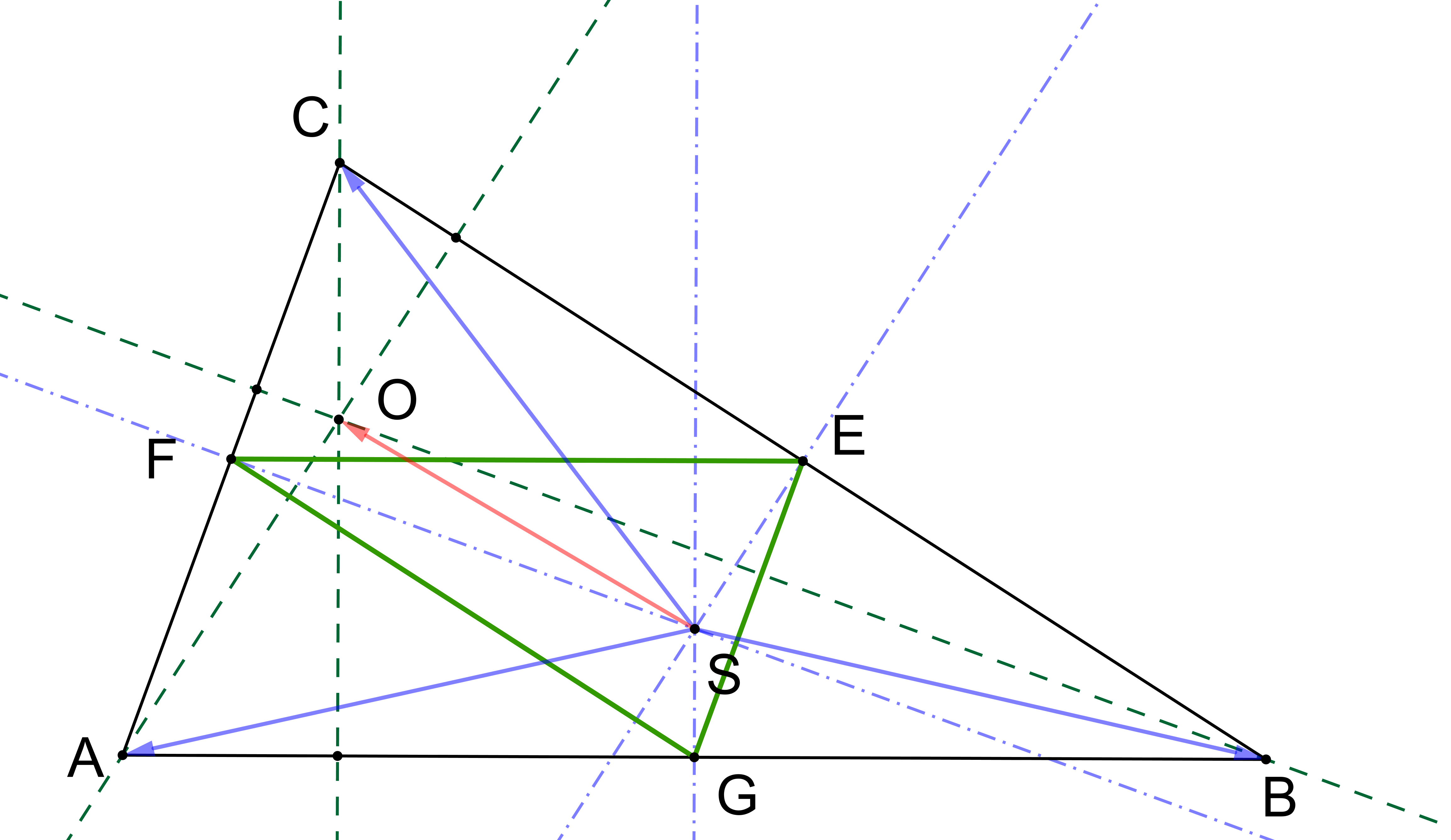 Prémiový úkol č. 8 - Řešení: Sečteme-li postupně vektory SA, SB, SC (vytváříme z nich "řetěz", tj. do koncového bodu jednoho umístíme počáteční bod následujícího.) je zřejmé, že koncový bod posledního z nich, vektoru SC, leží na výšce vc trojúhelníku ABC. Jde tedy "jenom" o to, ukázat, že leží právě v bodě O. To, jak vidíme na obrázku nastane tehdy, když |CO|=|SE|. To ale plyne například ze skutečnosti, že trojúhelník EFG je podobný trojúhelníku ABC s poměrem podobnosti 1/2 (jeho strany jsou středními příčkami trojúhelníku ABC) a že bod S je jeho ortocentrum (osy stran trojúhelníku ABC jsou výškami trojúhelníku EFG, kde výškami rozumíme přímky jdoucí vrcholy trojúhelníku kolmo na protilehlé strany).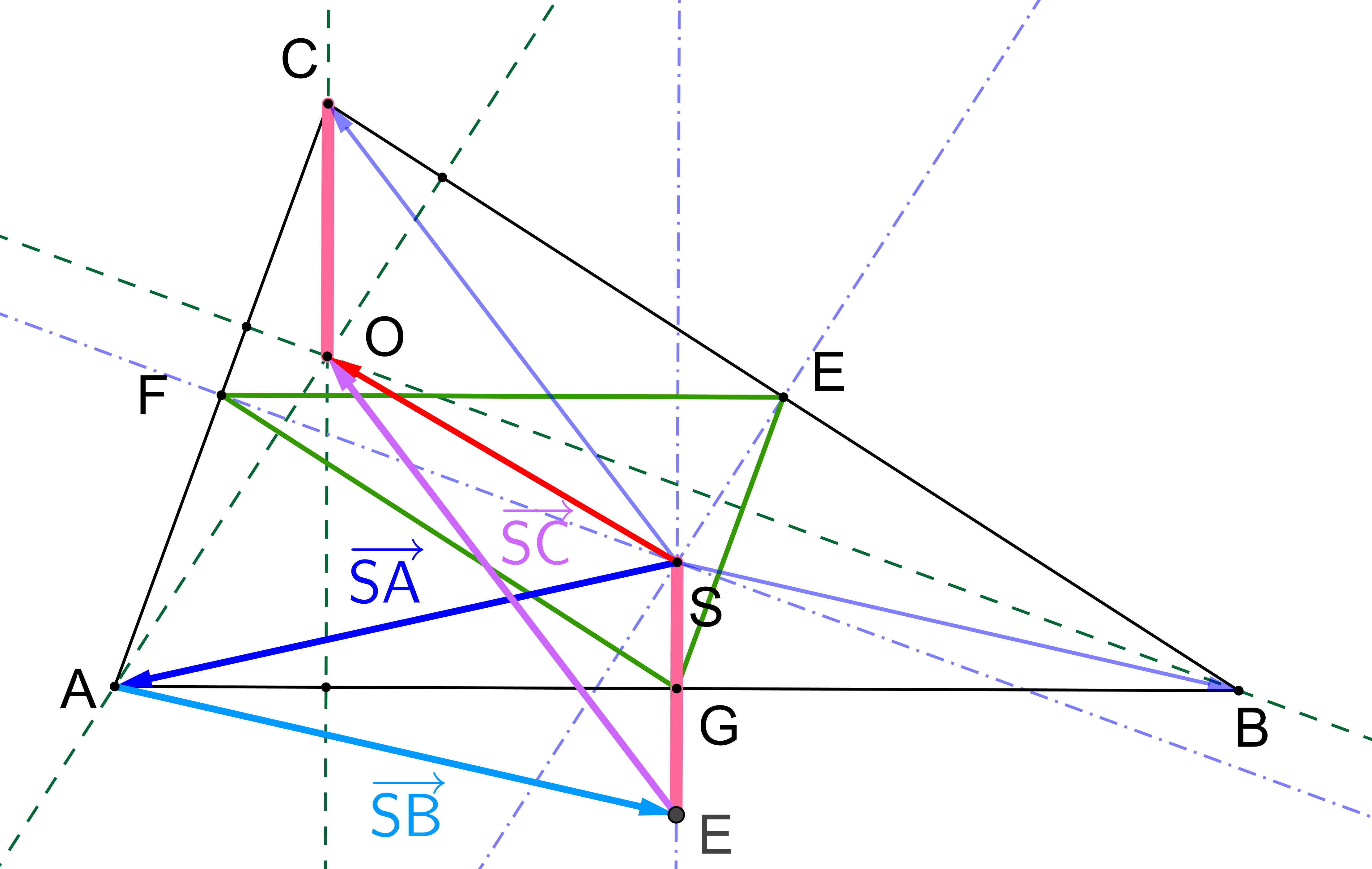

  9. týden / 13. 4.-17. 4. / Samostudium: Posunutí. Posunuté zrcadlení. Zde je zadání samostatné práce pro 9. týden: Prostudujte prosím následující text "Posunutí. Posunuté zrcadlení. Identita" a co nejlépe vyřešte příklady a cvičení vysazené modrou barvou. K zaznamenání Vašeho postupu při jejich řešení použijte prostředky dle vlastní úvahy, papír a tužku, GeoGebru a textový editor nebo jakýkoliv jiný vhodný software. Konstrukční úlohy můžete řešit v GeoGebře, vždy však k nim udělejte i rozbor, ručně, tužkou na papír. Rozbor udělejte, i když nevíte, jak úlohu řešit! Řešení pošlete v rámci týmu v aplikaci Teams. V případě nejasností se ptejte, použijte prostředí Teams nebo e-mail. Užitečné odkazy: How to translate a triangle using a transformation vector (video) Transformations - Translating A Triangle On The Coordinate Plane (video) Glide Reflections - Concept (video) GeoGebra: Návody Introduction to GeoGebra (webinar-video) Prémiový úkol č. 9:  V konvexním čtyřúhelníku ABCD je úhlopříčka BD osou vnitřního úhlu ∠ABC a dále platí |AC|=|BC|. Velikost úhlu ∠BDC je 80° a velikost úhlu ∠ACB je 20°. Určete velikost úhlu ∠BAD! 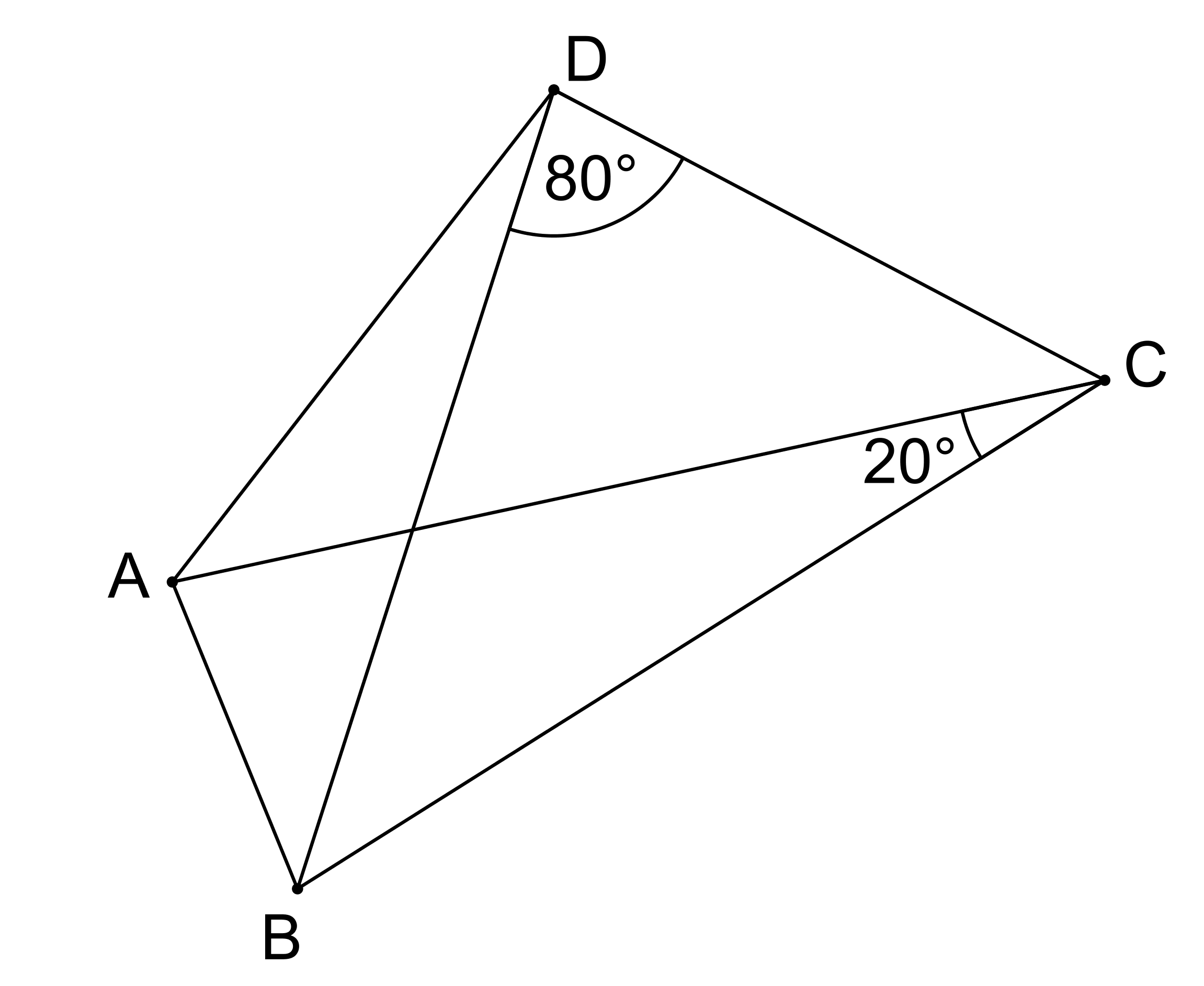Prémiový úkol č. 9 - Řešení: Viz obrázek. Celkem snadno zjistíme velikosti úhlů, které v obrázku figurují, s výjimkou vnitřních úhlú trojúhelníku DAE při vrcholech D a A, o kterých víme, že jejich součet je 60°. O jejich velikostech nám pomohou rozhodnout podobnosti trojúhelníků, které vyplňují daný čtyřúhelník. Konkrétně je zjevné, že trojúhelník ABE je podobný trojúhelníku DCE. Potom ale musí být trojúhelník ADE podobný trojúhelníku BCE. Pak už je jasné, že při vrcholu A je úhel 40° a při D je 20°.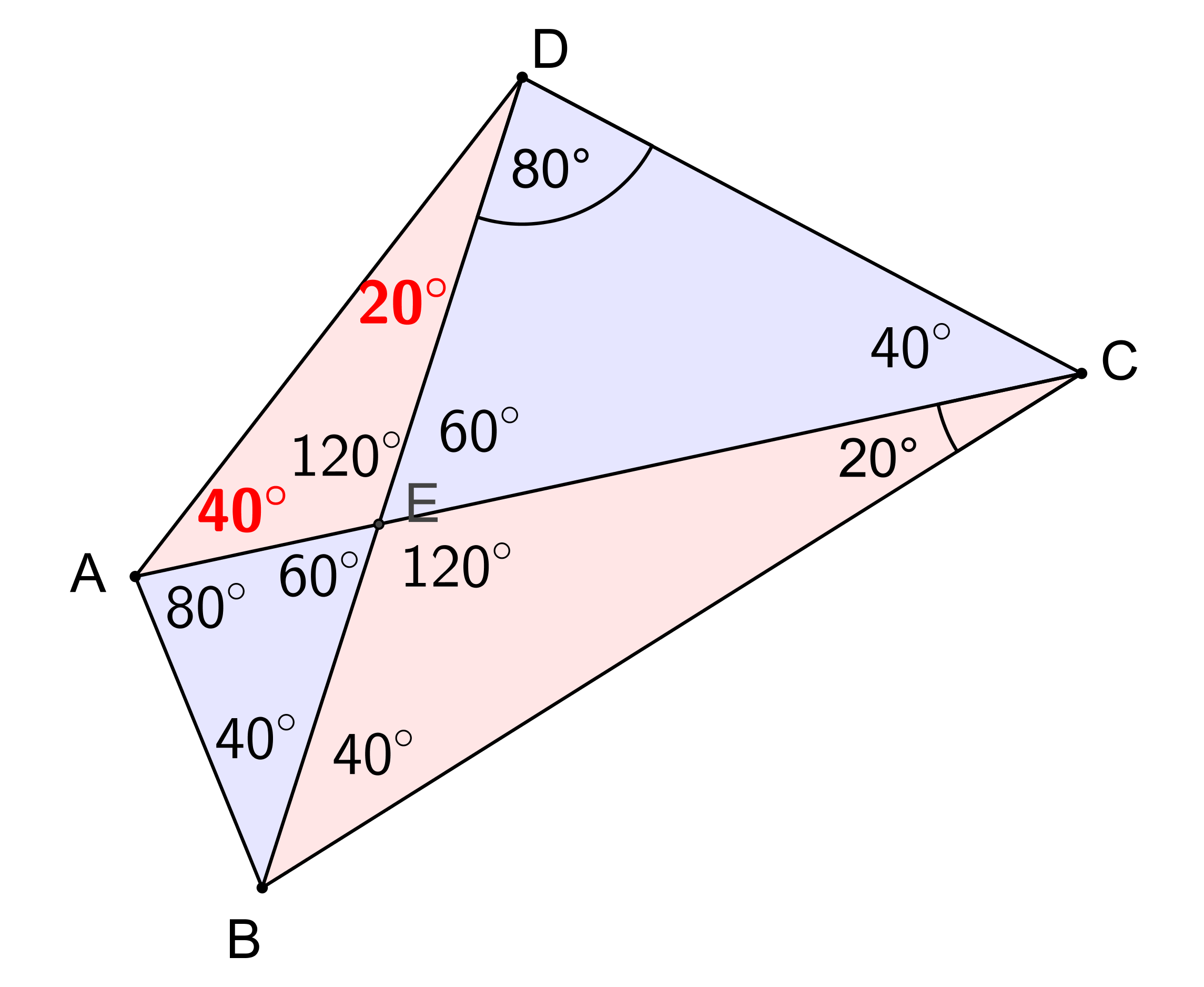

  10. týden / 20. 4.-24. 4. / Samostudium: Skládání zobrazení. Klasifikace shodností. Zde je zadání samostatné práce pro 10. týden: Prostudujte prosím následující text "Skládání zobrazení. Klasifikace shodností." a co nejlépe vyřešte příklady a cvičení vysazené modrou barvou. K zaznamenání Vašeho postupu při jejich řešení použijte prostředky dle vlastní úvahy, papír a tužku, GeoGebru a textový editor nebo jakýkoliv jiný vhodný software. Konstrukční úlohy můžete řešit v GeoGebře, vždy však k nim udělejte i rozbor, ručně, tužkou na papír. Rozbor udělejte, i když nevíte, jak úlohu řešit! Řešení pošlete v rámci týmu v aplikaci Teams. V případě nejasností se ptejte, použijte prostředí Teams nebo e-mail. Užitečné odkazy: Composition of Transformations (video) Compositions of Isometries (video) Prémiový úkol č. 10:  Ve čtyřúhelníku ABCD jsou úhlopříčkami AC a BD a jim protilehlými vrcholy tvořeny čtyři trojúhelníky ACD, DBC, CAB a BDA. Dokažte, že strany čtyřúhelníku EFGH, kde E, F, G a H jsou v daném pořadí těžiště uvedených trojúhelníků, jsou rovnoběžné se stranami čtyřúhelníku ABCD a jejich délky jsou třetinami těchto stran. 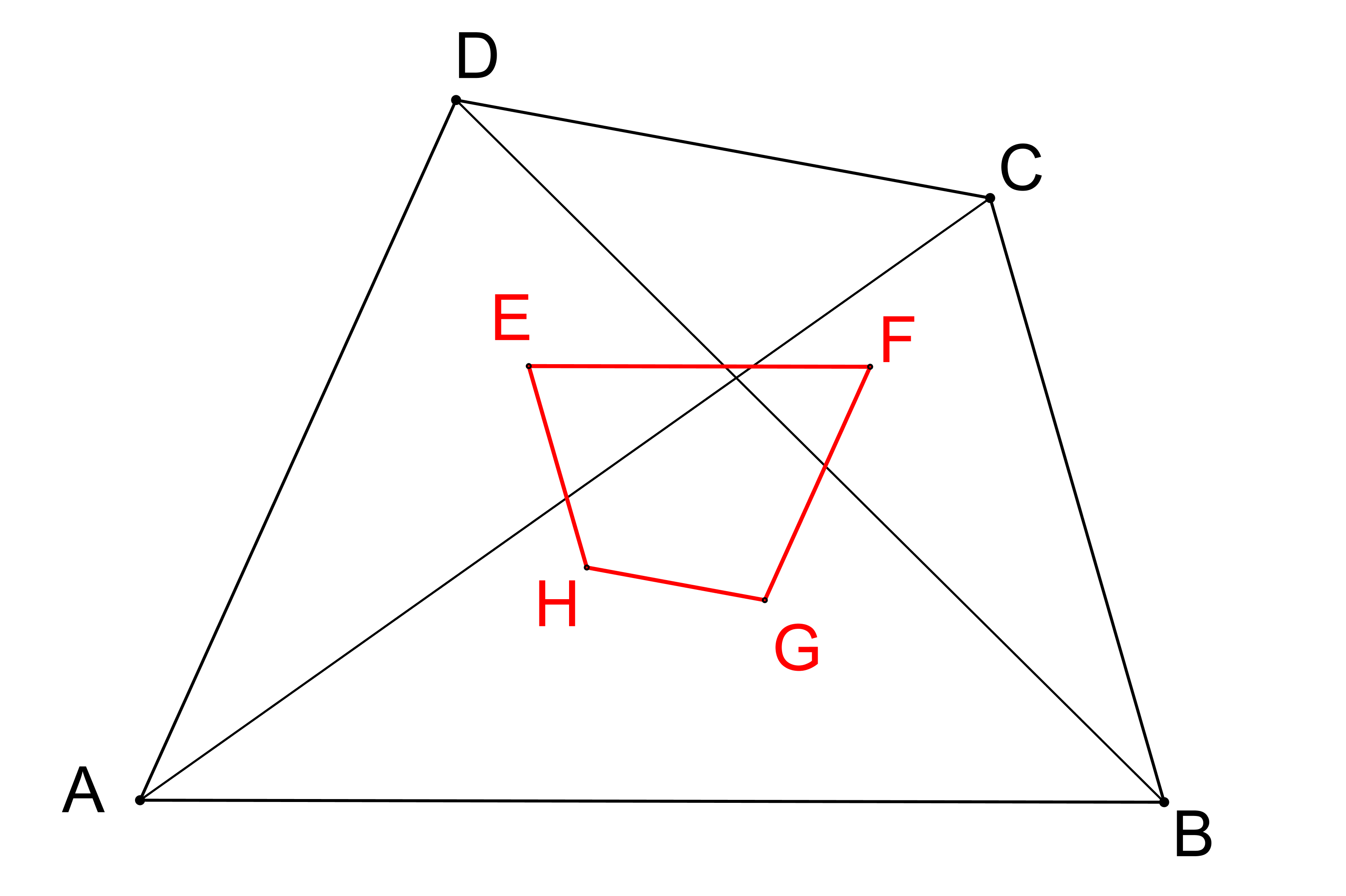Prémiový úkol č. 10 - Řešení: Existuje více způsobů, jak úlohu řešit. Ukáži zde takový, který nikdo z řešitelů nepoužil. Využiji k tomu vztah T=(A+B+C)/3 pro výpočet souřadnic těžiště T trojúhelníku ABC. Podle zadání úlohy pak platí E=(A+C+D)/3 a F=(D+C+B)/3 a vektor F-E, jehož umístěním je úsečka EF, má souřadnice F-E=(D+C+B)/3-(A+C+D)/3=(B-A)/3. Vidíme, že F-E je skutečně rovnoběžný s B-A a je třikrát menší. Analogicky dokážeme tyto vlastnosti i pro zbývající tři strany čtyřúhelníku EFGH.

  11. týden / 27. 4.-1. 5. / Samostudium: Každou shodnost v rovině lze složit z nejvýše tří osových souměrností. Zde je zadání samostatné práce pro 11. týden: Prostudujte prosím následující text "Tři osové souměrnosti stačí". Jeho obsah využijte k přípravě na zkoušku dle zveřejněných otázek a příkladů. V případě nejasností mne bez váhání kontaktujte. Prémiový úkol č. 11:  V rovině je dán čtverec ABCD. Kružnice k prochází body A, B a dotýká se přímky CD. Označme M průsečík kružnice k a strany BC (různý od B), viz obrázek. Určete poměr |CM|:|MB|. 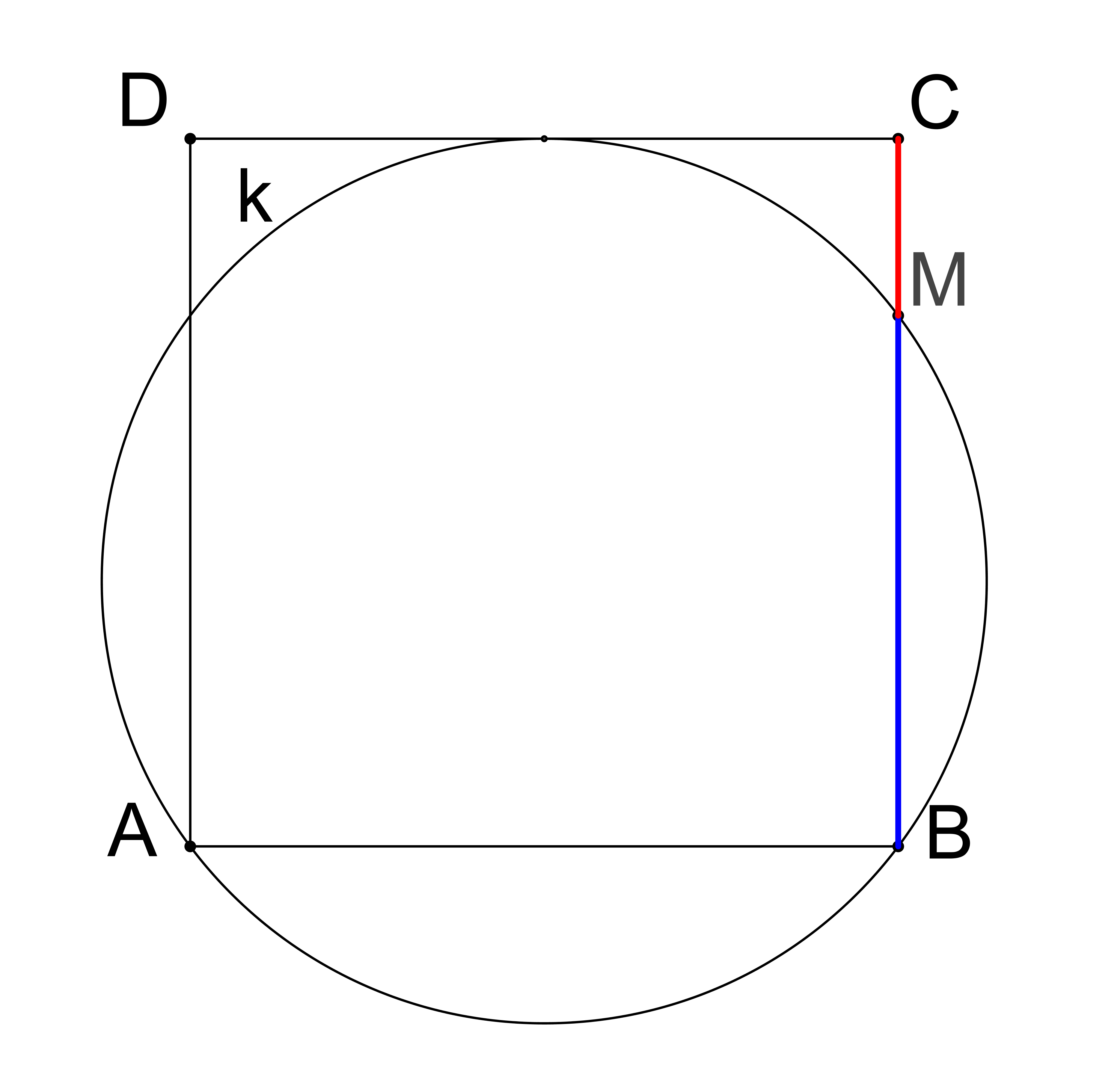Prémiový úkol č. 11 - Řešení: Trojúhelníky AED a EMC, viz obrázek, jsou podobné (Existuje věta, která říká, že jsou-li ramena dvou úhlů po dvojicích vzájemně kolmá, tyto úhly jsou shodné. To je situace vyznačených vnitřních úhlů uvedených trojúhelníků.). Potom platí |AD|/|EC| = |DE|/|CM|, po dosazení a/(a/2)=(a/2)/|CM|, odkud po úpravě plyne |CM|=a/4. Pro poměr |CM|:|MB| tedy platí |CM|:|MB| = 1:3.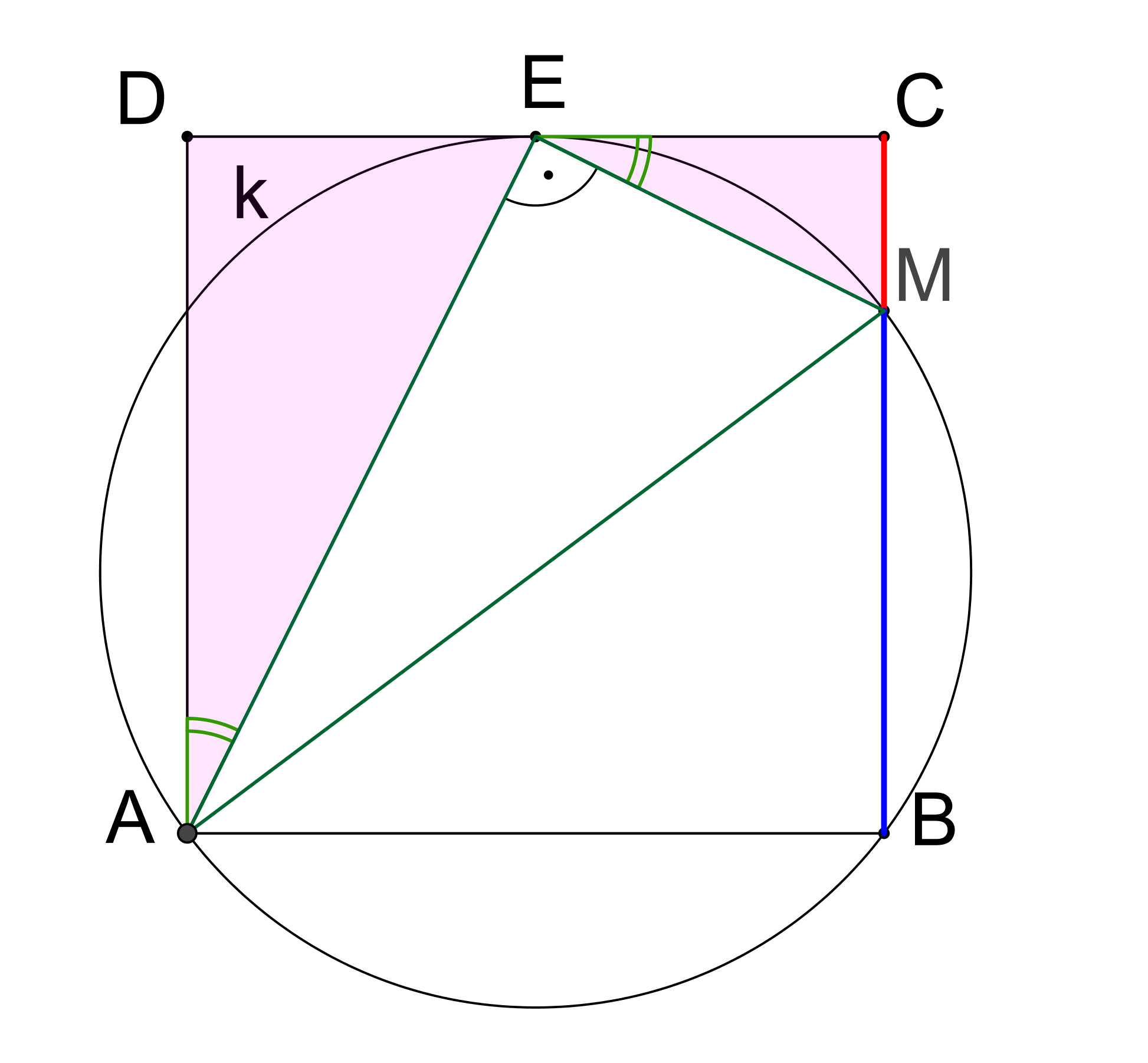

  12. týden / 4. 5.-8. 5. / Samostudium: Podobná zobrazení. Zde je zadání samostatné práce pro 12. týden: Prostudujte prosím následující text "Podobná zobrazení". Jeho obsah využijte k přípravě na zkoušku dle zveřejněných otázek a příkladů. V případě nejasností mne bez váhání kontaktujte. Prémiový úkol č. 12:  V rovině je dán pravoúhlý trojúhelník ABC takový, že kružnice k(A,|AC|) protíná přeponu AB v jejím středu S. Dokažte, že kružnice opsaná trojúhelníku BCS je shodná s kružnicí k. 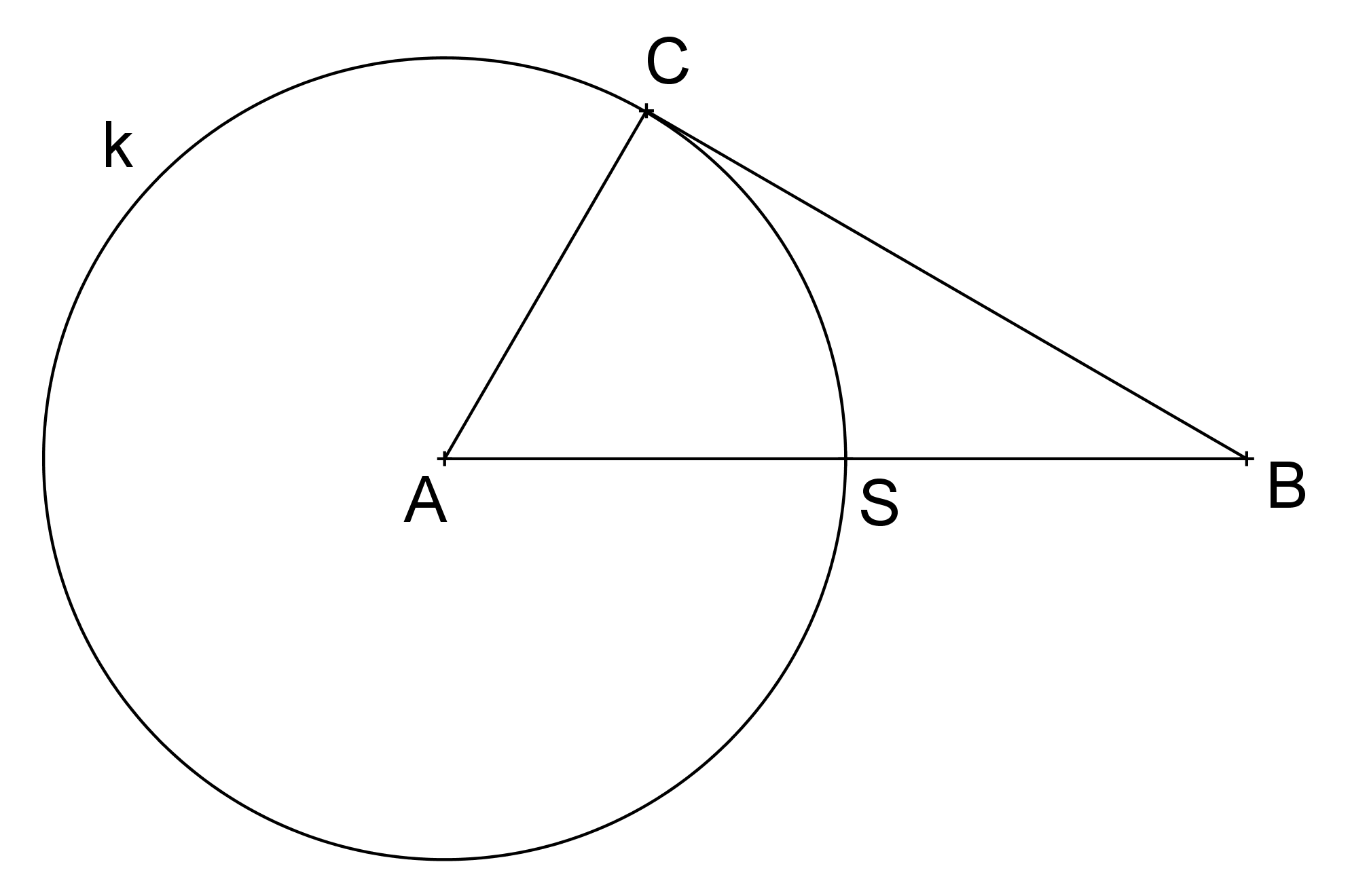Prémiový úkol č. 12 - Řešení: Stačí dokázat, že tři barevné trojúhelníky na obrázku níže jsou shodné rovnostranné trojúhelníky. Při použití Thaletovy kružnice a skutečností, že součet vnitřních úhlů v trojúhelníku je 180° a že osa tětivy prochází středem kružnice to není nijak obtížné.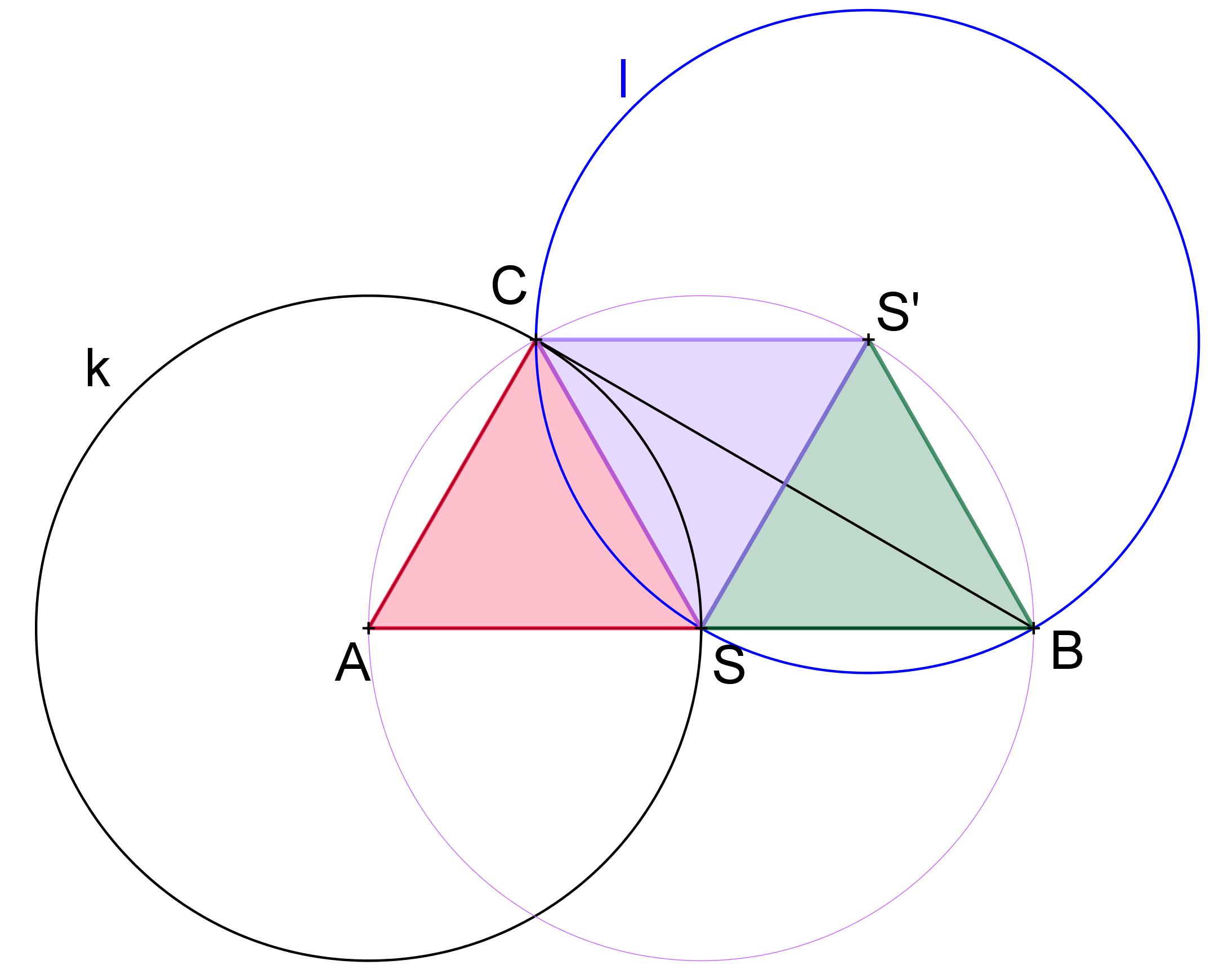

  13. týden / 10. 5.-15. 5. / Samostudium: Stejnolehlost. Zde je zadání samostatné práce pro 13. týden: Prostudujte prosím následující text "Stejnolehlost." Jeho obsah využijte k přípravě na zkoušku dle zveřejněných otázek a příkladů. V případě nejasností mne bez váhání kontaktujte. Použijte prostředí Teams nebo e-mail. Po domluvě je možná osobní konzultace. Prémiový úkol č. 13:  Dvě spolu pevně spojená kola o různých poloměrech, větší o poloměru R, menší o poloměru r, se pohybují každé po své dráze, které jsou vzájemně rovnoběžné, viz obrázek. Větší kolo urazí dráhu 2πR, menší potom 2πr. Z obrázku je zřejmé, že 2πR = 2πr, tj. R = r, což ale neplatí. Kde je chyba? 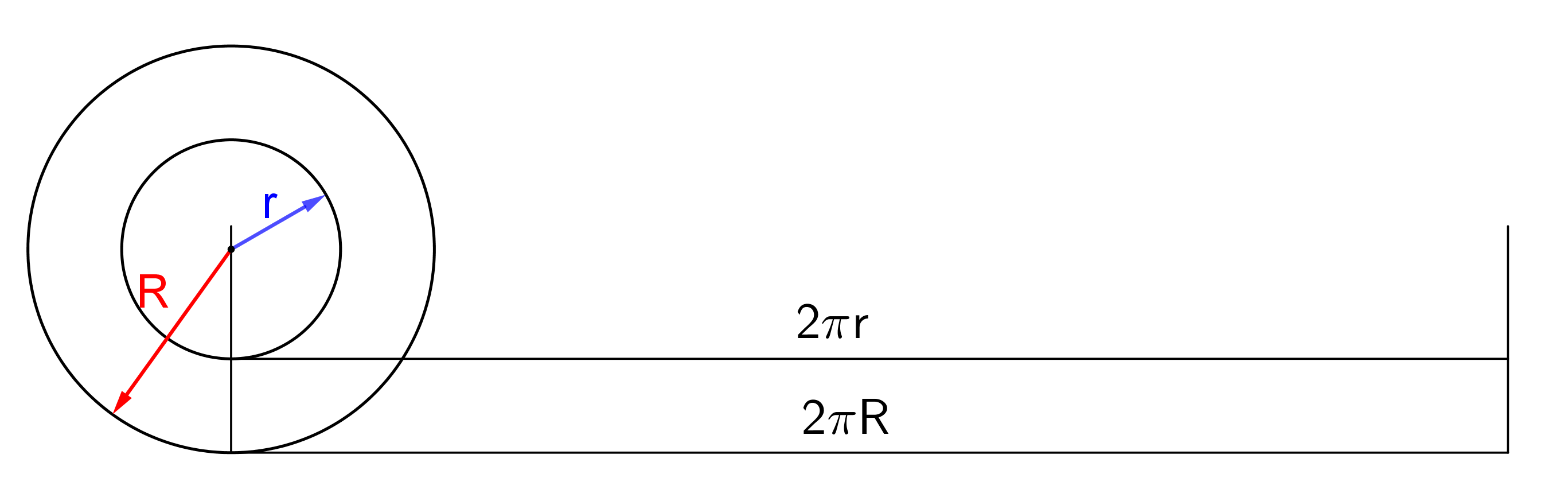Prémiový úkol č. 13 - Řešení: Obě kola se nemohou současně odvalovat (tj. pohybovat bez smyku), jedno z nich prokluzuje. Dle uvedeného zadání je to to malé. Jedná se o problém - paradox, jehož zadání je připisováno Aristotelovi. Proto je znám jako Aristotelovo kolo, viz např. Aristotle's wheel paradox

  14. týden / 18. 5.-22. 5. / Samostudium: Mocnost bodu ke kružnici. Zde je zadání samostatné práce pro 14. týden: Prostudujte prosím následující text "Mocnost bodu ke kružnici." Jeho obsah využijte k přípravě na zkoušku dle zveřejněných otázek a příkladů. V případě nejasností mne bez váhání kontaktujte. Použijte prostředí Teams nebo e-mail. Po domluvě je možná osobní konzultace. Prémiový úkol č. 14:  Zadání (pdf)

  CVIČENÍ 5 (Shodnost. Osová souměrnost.) Příklad 1:  Rozhodněte, zda afinity dané uvedenými rovnicemi jsou shodnosti. Pokud ano, určete jaké (Využijte při tom samodružné body a směry těchto afinit). a) x' = -x + 4, y' = -y - 6, b) x' = x, y' = -y, c) x' = -4/5x + 3/5y + 8, y' = 3/5x + 4/5y - 6. Fermatův bod:  Bod, pro který je součet jeho vzdáleností od vrcholů trojúhelníku minimální. [en.wikipedia.org: Fermat point] [Konstrukce Fermatova bodu] Domácí úkol 2:  Řešte Příklad 1 c.

  PŘEDNÁŠKA 6 Osová souměrnost

• Otočení. Středová souměrnost. Posunutí. Posunuté zrcadlení. Skládání shodností. Shodnosti přímé a nepřímé. Grupa shodností. Klasifikace shodností v rovině.

  CVIČENÍ 7 (Osová souměrnost) Osová souměrnost - úlohy k řešení. Fagnanův problém: Danému ostroúhlému trojúhelníku vepište trojúhelník o nejmenším obvodu. [Fagnanův problém - řešení č. 1] [Fagnanův problém - řešení č. 2]

  PŘEDNÁŠKA 7 Osová souměrnost (pokračování).

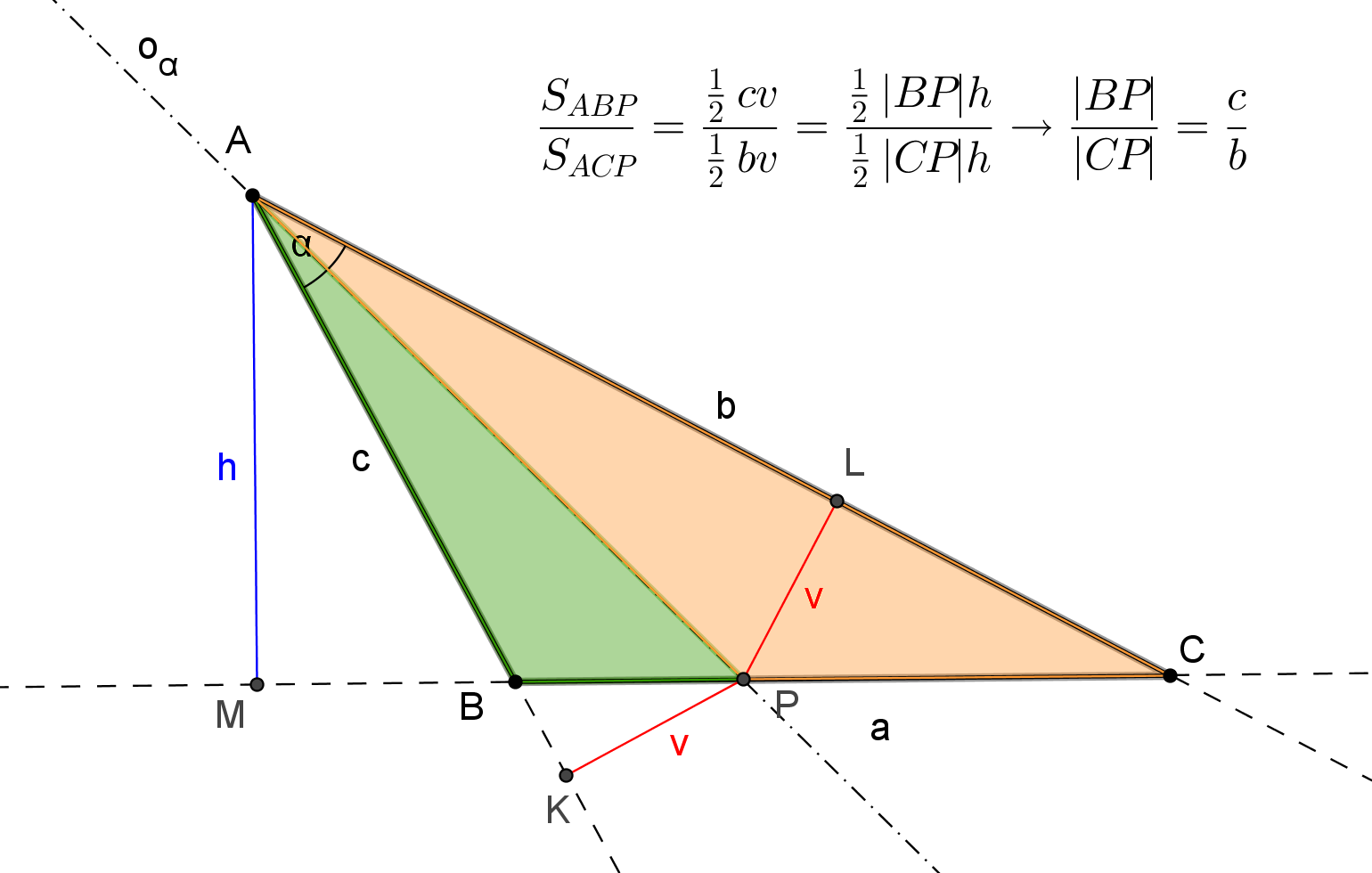
  CVIČENÍ 8 Příklad (Mascheroniova konstrukce): Je dána kružnice k(S;r); dále je dána dvěma body A, B (body neleží na kružnici) její sečna p, která neprochází středem S. Sestrojte průsečíky přímky p s kružnicí k, aniž přitom použijete pravítka. (Lorenzo Mascheroni, 1750-1800, Georg Mohr, 1640-1697, Mascheroni Construction) [Aplet pro provedení konstrukce] [Řešení]

  PŘEDNÁŠKA 8 Otočení.

  CVIČENÍ 9 Příklad:  Dokažte následující větu: V každém trojúhelníku dělí osa libovolného vnitřního úhlu protější stranu v poměru stran přilehlých. Otočení - úlohy k řešení. Středová souměrnost - úlohy k řešení.

  PŘEDNÁŠKA 9 Středová souměrnost. Úkol: S využitím uvedených apletů promyslete důkaz tvrzení "Každá shodnost se dá složit z nejvýše tří osových souměrností". Aplety: [přímá shodnost][nepřímá shodnost] Posunutí. Posunuté zrcadlení.

  CVIČENÍ 10 Posunutí - úlohy k řešení. Posunuté zrcadlení.

  PŘEDNÁŠKA 10 Skládání shodností. Shodnosti přímé a nepřímé. Grupa shodností.

• Stejnolehlost. Skládání stejnolehlostí v rovině. Stejnolehlost kružnic. Podobné transformace roviny.

  CVIČENÍ 11 Úlohy na shodnosti v rovině - Vzorové příklady KMA/PLA 2015

  PŘEDNÁŠKA 11 Klasifikace shodností v rovině. (Odvození analytického vyjádření afinity v rovině.) Shodnosti v rovině - úlohy.

  CVIČENÍ 12 Stejnolehlost kružnic. Aplety: [Mongeova věta] [Eulerova přímka a kružnice devíti bodů] Stejnolehlost - úlohy k řešení. [Řešení vzorového příkladu č. 15 (bod-přímka-kružnice)] [Řešení vzorového příkladu č. 16 (bod-přímka-přímka)] [Řešení vzorového příkladu č. 17 (kružnice-přímka-přímka)]

  PŘEDNÁŠKA 12 Podobné zobrazení. Stejnolehlost. Skládání stejnolehlostí v rovině. Aplet: [Skládání stejnolehlostí] Podobnosti eukleidovské roviny.

• Shodnosti a podobnosti v konstrukčních úlohách.
• Mocnost bodu ke kružnici. Osová afinita.

  CVIČENÍ 13 Mocnost bodu ke kružnici - úlohy k řešení. [Řešení vzorového příkladu č. 1 užitím mocnosti bodu ke kružnici a pomocné kružnice] [Řešení vzorového příkladu č. 1 užitím mocnosti bodu ke kružnici a Eukleidovy věty o odvěsně]

  PŘEDNÁŠKA 13 Mocnost bodu ke kružnici.

Literatura

[1] Sekanina, M. a kol.: Geometrie II, SPN, Praha 1988.
[2] Pomykalová, E., Matematika pro gymnázia - Planimetrie. Prometheus, Praha, 2008.
[3] Kuřina, F.: 10 geometrických transformací. Prometheus, Praha, 2002.
[4] Sekanina, M. a kol.: Geometrie I, SPN, Praha 1988.
[5] Leischner, P. Geometrická zobrazení, Jihočeská univerzita v Českých Budějovicích, 2010.
[6] Pech, P., Klasické vs. počítačové metody při řešení úloh v geometrii, České Budějovice, PF JU, 2005.
[7] Kuřina, F.: 10 pohledů na geometrii. Akademie věd České republiky, 1996.
[8] Audin, M.: Geometry, Springer, 2003.
[9] Budinský, B.: Analytická a diferenciální geometrie. SNTL, Praha, 1983.
[10] Pech, P., Analytická geometrie lineárních útvarů, České Budějovice, PF JU, 2004.
[11] Voráčová a kol., Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha, 2012.
[12] Vyšín, J. . a kol.: Geometrie pro pedagogické fakulty II, Bratislava, 1970.
[13] Eukleides, Eukleidovy základy (Elementa), překlad F. Servít, 1907.
Dostupné na https://commons.wikimedia.org/wiki/File:Eukleides_Servit.pdf
[14] Leydold, J., Petry, M. : Introduction to Maxima for Economics (pdf) [online]
[15]  Hašek, R., Noruláková, M.: Program wxMaxima ve výuce matematiky (pdf) [online]. Sborník příspěvků 5. konference Užití počítačů ve výuce matematiky, 2011.

Internetové odkazy

Software ke stažení

www.geogebra.org ... program GeoGebra (zdarma)
wxmaxima-developers.github.io/wxmaxima ... program wxMaxima (zdarma)

Materiály pro výuku a sebevzdělávání

i2geo.net ... portál pro sdílení výukových materiálů dynamické geometrie
wiki.geogebra.org ... GeoGebra Wiki - manuál, výukové materiály, fórum apod.
wiki.geogebra.org/cs/ ... postupně překládaná česká verze GeoGebra Wiki
www.youtube.com/user/GeoGebraChannel ... GeoGebra na YouTube
www.geogebratube.org ... Materiály v GeoGebře ke stáhnutí
www.cut-the-knot.org ... Interactive Mathematics Miscellany and Puzzles
http://www.math.uoc.gr ... Geometrikon - galerie geometrických témat

Požadavky na studenta

• Zkouška, varianta 2020
  • Zkouška má dvě části, písemnou a ústní, které se vykonávají v jeden den. Začíná se písemnou částí, ústní částí lze pokračovat pouze po úspěšném vypracování písemné části (tj. hodnocení nejhůře 3). Písemná část zkoušky se skládá ze tří příkladů (viz vzorové příklady), u konstrukčních úloh je kromě rozboru požadován popis konstrukce nebo její provedení, proto je vhodné přinést si rýsovací potřeby. Otázka k ústní části bude losována ze zveřejněných 12 otázek (viz Otázky ke zkoušce KMA/PLA 2020).

    Aktuální verze otázek a vzorových příkladů:
    [Otázky ke zkoušce KMA/PLA 2020]     [Vzorové příklady KMA/PLA 2020]

    Návody k řešení vybraných příkladů:
    Řešení vzorového příkladu č. 10 (užití mocnosti bodu ke kružnici a pomocné kružnice)
    Řešení vzorového příkladu č. 10 (užití mocnosti bodu ke kružnici a Eukleidovy věty o odvěsně)
    Řešení vzorového příkladu č. 12 (bod-přímka-kružnice)
    Řešení vzorového příkladu č. 13 (bod-přímka-přímka)
    Řešení vzorového příkladu č. 14 (kružnice-přímka-přímka)

  • Podmínky řešení prémiových příkladů: Srozumitelný a přehledný zápis řešení problému, pochopitelně doplněný alespoň jedním obrázkem, můžete posílat během 1 týdne následujícího po dni zadání (zadání proběhne vždy na přednášce) na adresu hasek@pf.jcu.cz. Dokument obsahující řešení může mít libovolnou formu, od oskenování ručně psaného řešení až po text napsaný v textovém editoru. Vždy se však musí jednat o autentický text vypracovaný tím, kdo dokument posílá. Prvních pět autorů správných řešení bude odměněno zvýhodněním 0.25 klasifikačního stupně při hodnocení zkouškové písemky (Přehled řešitelů prémiových úkolů).