Matematika I - KMA/8M1

Předmět Matematika I je věnován detailnímu seznámení se základy elementární geometrie v rovině a v prostoru. Pozornost je věnována především shodným a podobným zobrazením, vzájemným polohám geometrických útvarů, způsobům jejich zobrazování a postupům určování jejich rozměrů, vzdáleností a odchylek.

Kompletní učební text ve formátu PDF: Hašek: Úvod do geometrie (poslední aktualizace 3. 10. 2019).

Osnova předmětu

• Úvod do geometrie.

  Přednáška:	Kapitoly 1-3 4 principy Františka Kuřiny a 5 van Hieleho úrovní chápání geometrického učiva Jakou geometrickou vlastnost znázorňují následující obrázky?
  Cvičení:	Zadání úloh pro cvičení. Vizuální důkaz Pythagorovy věty z přednášky / Perigalův důkaz Pythagorovy věty / Henry Perigal (1801-1898) J. V. Sedláček: Základy měřičství (1822) O. Byrne: The Elements of Euclid (B. VI, P. VIII)(1847) Důkaz vztahu pro výpočet obsahu kruhu: Area of a circle, how to get the formula (video)

• Geometrické útvary v rovině.

  Přednáška:	Kapitola 4
  Cvičení:	Zadání úloh pro cvičení. Spiral of Theodorus (Wikipedia)

• Mnohoúhelníky.

  Přednáška:

  Kapitola 4 Vnější úhel trojúhelníku

  Cvičení:

  ÚKOL: Kolik různých trojúhelníků (všechny vzájemně shodné uvažujeme jako jeden) můžeme vytvořit na geoboardu 3x3? Umíte je všechny pojmenovat (tj. použít pojmy pravoúhlý, rovnoramenný, tupoúhlý, ...)? Umíte u všech určit obsah (pokud předpokládáme, že vzdálenost sousedních kolíků desky je 1)? Zkuste to! Trojúhelníky nakreslete, opatřete výpočty obsahů a vložte do Teams, dle zadání, které tam bude publikované. Můžete použít tento online Geoboard. Více o této důležité pomůcce viz např. https://en.wikipedia.org/wiki/Geoboard. ÚKOL: Dle uvedeného obrázku si vyrobte Tangram (pokud tento hlavolam již nevlastníte) a pokuste se, užitím všech jeho součástí, jak stanoví pravidla, vytvořit co nejvíce různých konvexních n-úhelníků. Nafoťte nebo nakreslete a vložte do Teams, dle zadání, které tam bude publikované. Online tangram Zadání úloh pro cvičení.

  Přednáška:	Kapitola 4 ÚKOL: Co mají uvedené dva obrázky (a tojúhelníky na nich zobrazení) společné a čím se liší? 0,0 –o+←↓↑→ A B C A1 B1 C1 0,0 –o+←↓↑→ A B C A1 B1 C1 T
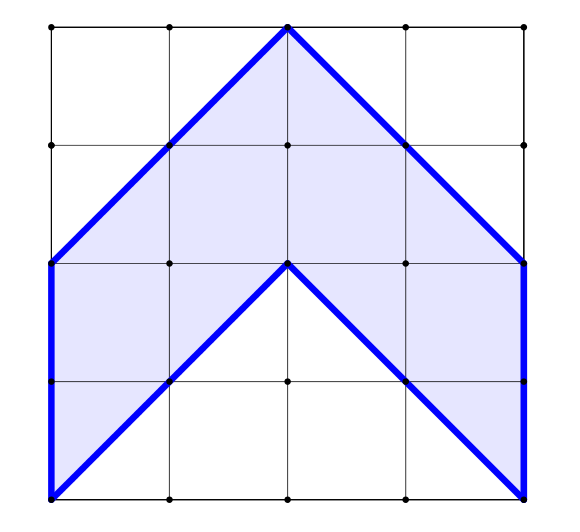
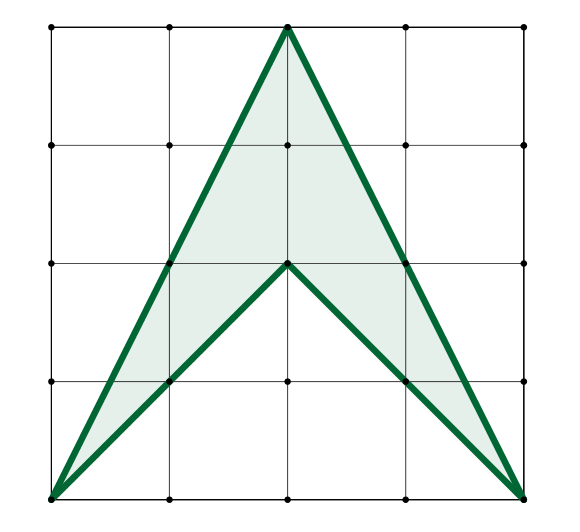
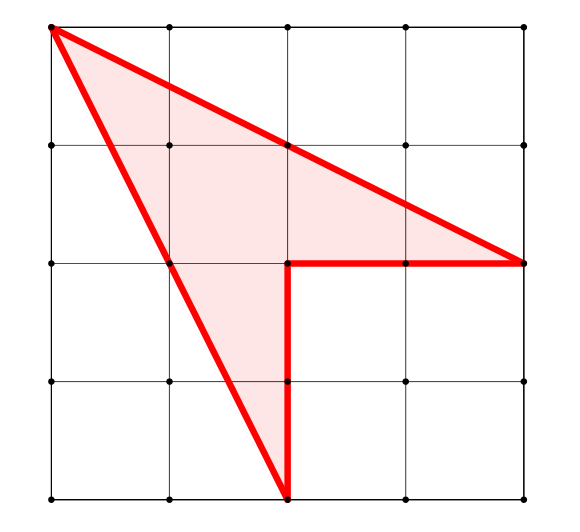
  Cvičení:	ÚKOL: Vypočítejte obsahy uvedených obrazců. Zadání úloh pro cvičení (Cvičení 4).   [Řešení cvičení 4] Literatura pro další studium: Jordánová, D. Obsah a obvod obrazce s využitím čtvercové sítě ve výuce geometrie na 1. stupni ZŠ. Závěrečná práce DVPP - Učitelství pro 1. stupeň ZŠ. České Budějovice: Jihočeská univerzita v Č. B. 2020.

• Délka úsečky. Dimenze prostoru. Obsah. Využití čtvercové sítě. Měření úhlu.

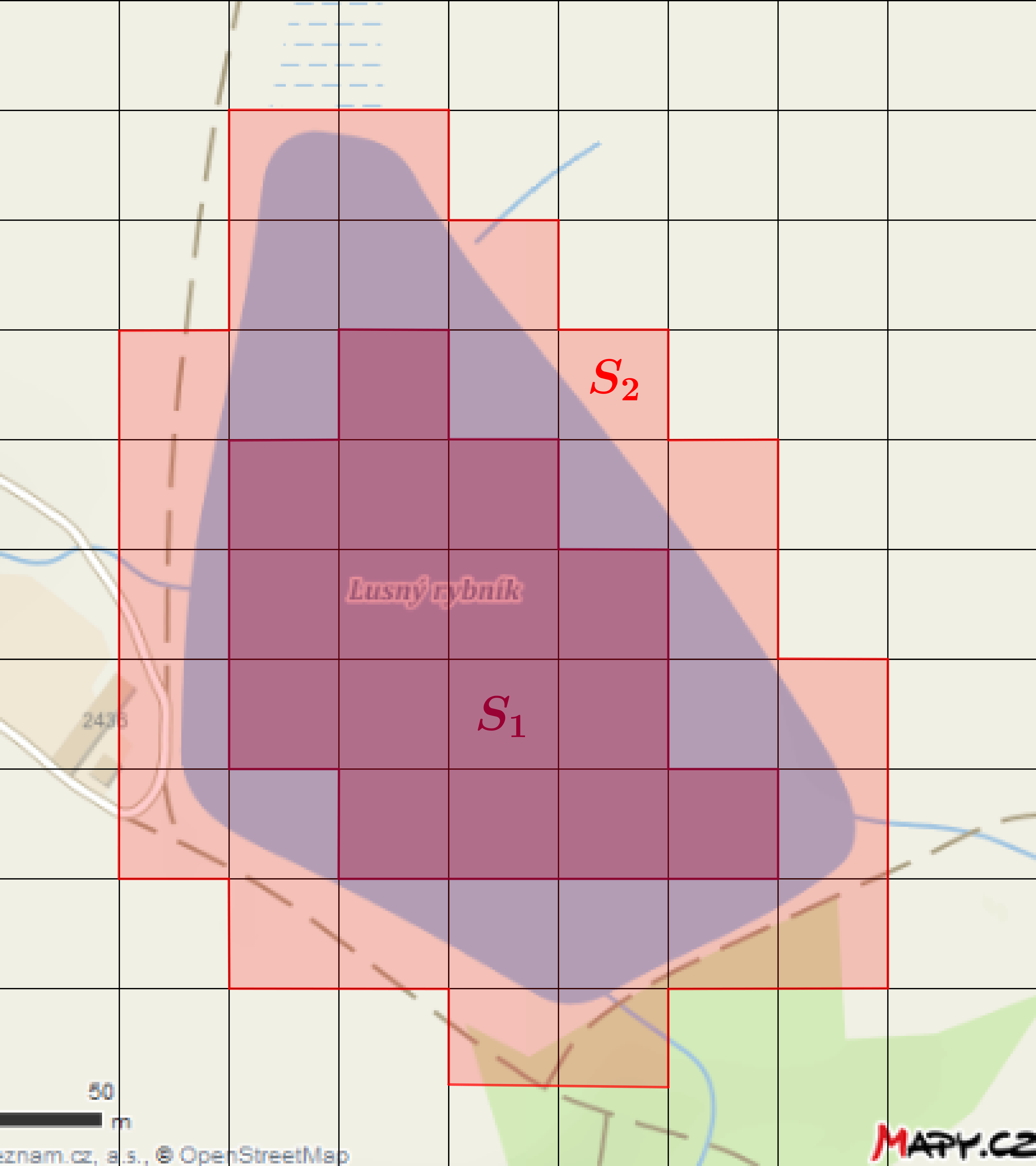
  Přednáška:	Kapitoly 6 (dimenze), 7 (míra), 5 (mnohostěny) a 4 (mnohoúhelníky) Rybník Lusný (Mapy.cz) [Lusný - čtvercová síť]
  Cvičení:	ÚKOL: Vyhlédněte si nějakou vysokou stavbu, sochu či strom a s užitím podobnosti trojúhelníků určete její výšku. Vytvořte fotografickou dokumentaci (alespoň jeden snímek) a své výpočty i s postupem zapište.

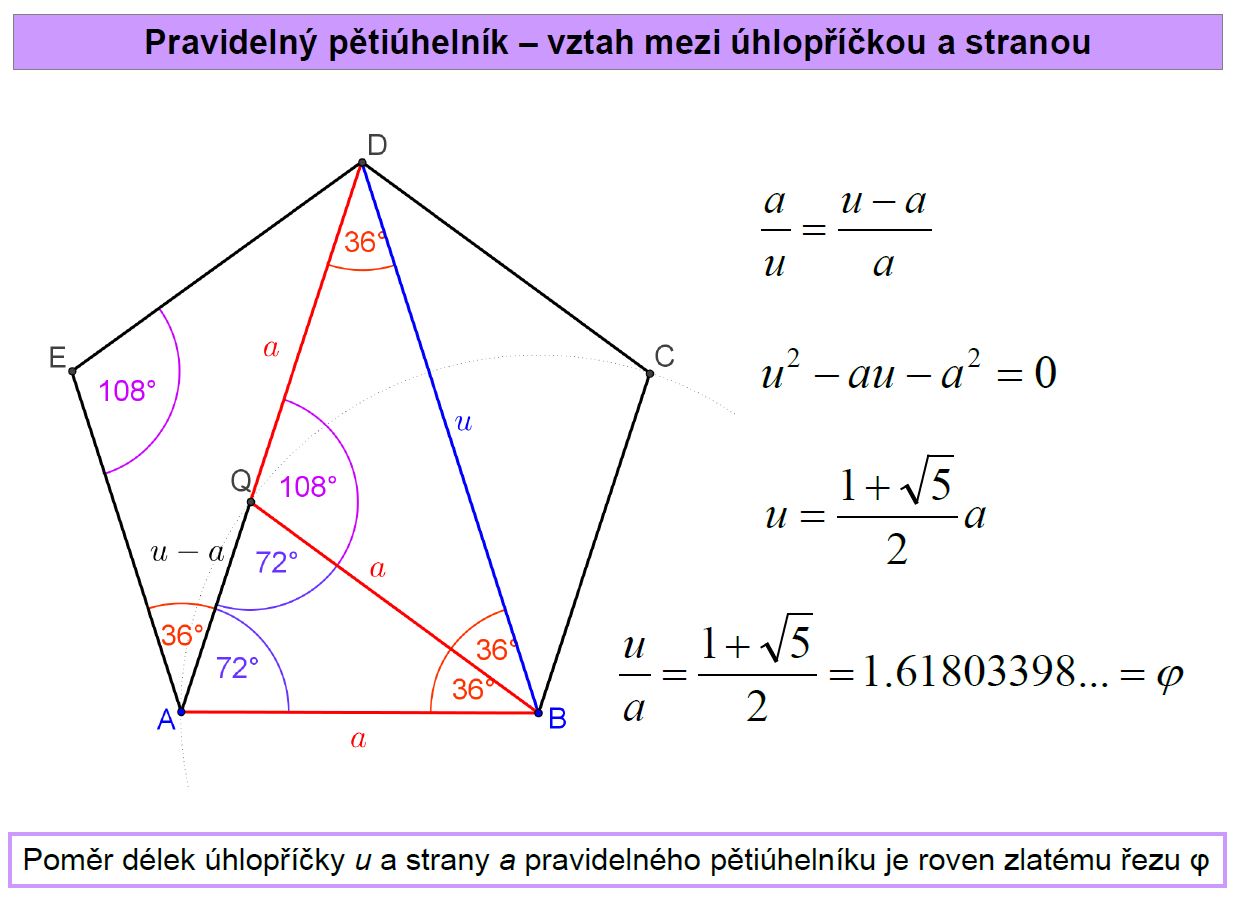
• Pravidelné mnohoúhelníky. Pokrytí roviny. Symetrie.

  Přednáška:	Kapitoly 4.8 (pravidelné mnohoúhelníky), 5 (mnohostěny)
  Cvičení:	Sítě těles: [Kosý hranol]   [Pětiboký jehlan] Zadání úloh pro cvičení (Cvičení 6).   [Řešení cvičení 6] [Cvičení 6 - Příklad 16 - Rotační kužel (GeoGebra)]

• Geometrické útvary v trojrozměrném prostoru.
• Stereometrie. Zobrazení trojrozměrného útvaru. Volné rovnoběžné promítání.
• Sdružené průměty trojrozměrného útvaru. Stavby z krychlí. Kótované promítání.

  Přednáška:

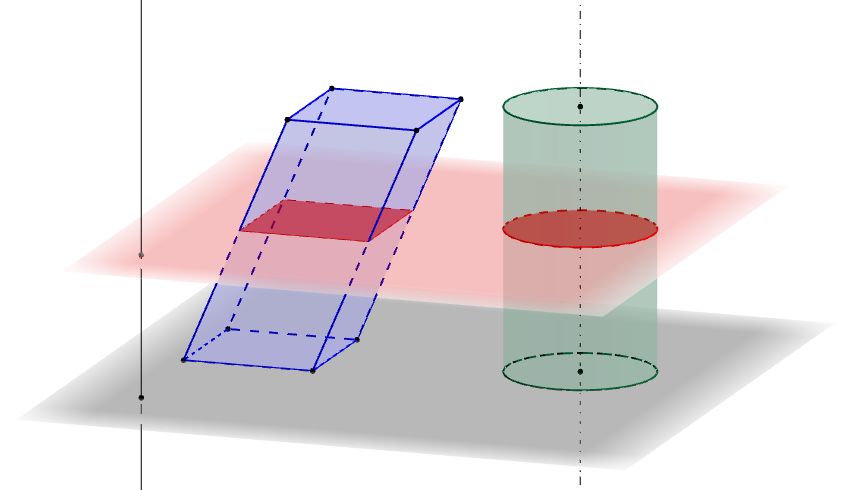
  Kapitoly 5, 11, 16 Krychle prince Ruprechta The trouble with five Pravidelné mnohostěny. Eulerův vztah. (prezentace) / Euler's Formula (www stránka) Cavalieriho princip / Cavalieri's principle (Wikipedia)

  Cvičení:

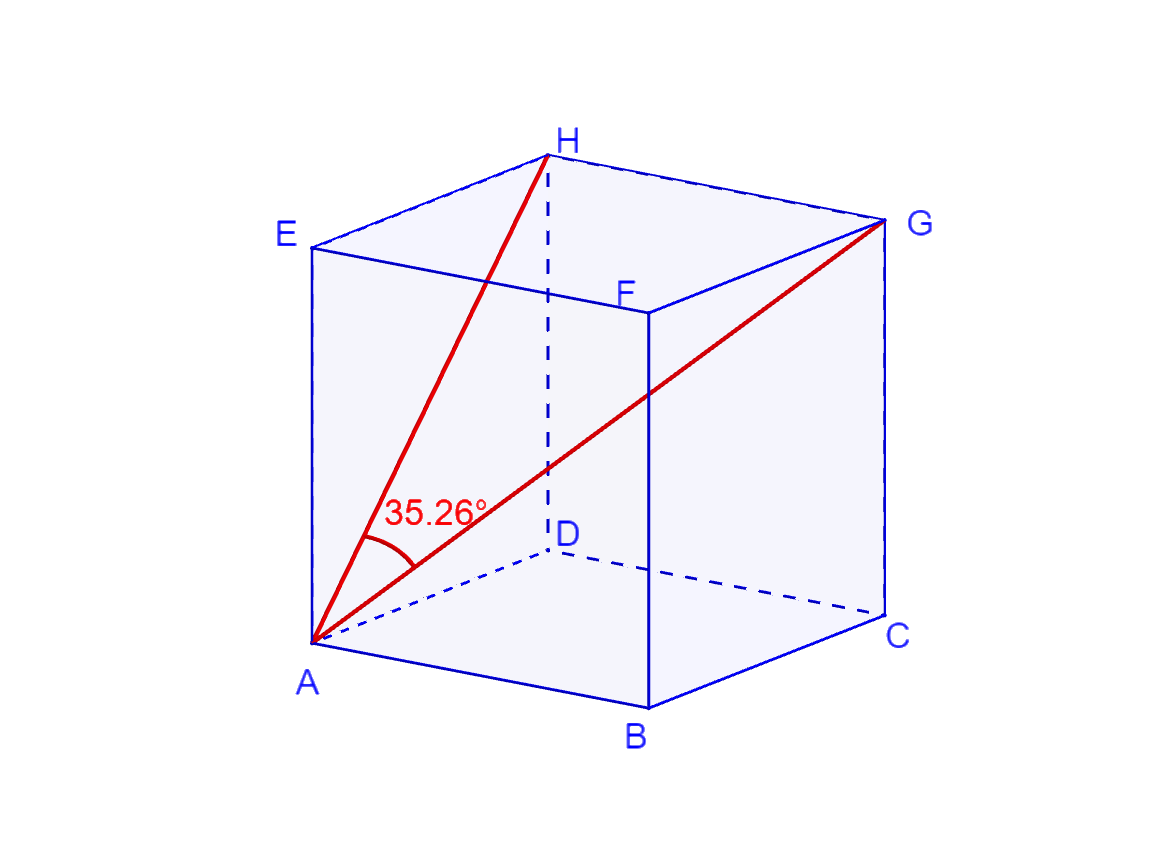
  Jak vypočítáme odchylku mezi stěnovou a tělesovou úhlopříčkou v krychli? [GeoGebra applet] Zadání úkolu pro cvičení: Na stránce Paper Models of Polyhedra si vyberte mnohostěn, vytiskněte si jeho síť a slepte model. Pokud se rozhodnete pro mnohostěn, který má méně než 10 stěn, vyberte si k němu ještě alespoň jeden další, tak, aby součet počtů jejich stěn byl alespoň 10. Výsledek nafoťte a vložte do MS Teams, kde bude tento úkol rovněž zadán.

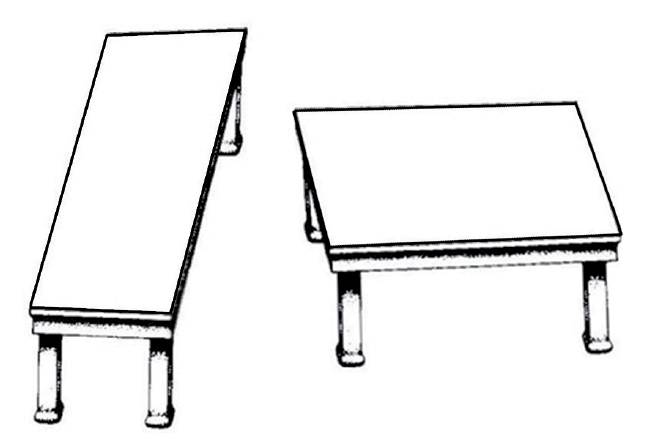
  Přednáška:	Rovnoběžné promítání. Středové promítání Kapitola 16 LN: Matematika pro páťáky Stavba z krychlí (str. 94) nárys - půdorys - bokorys Úkol:  Načrtněte nárys, půdorys a bokorys pro každou z níže zobrazených staveb z krychlí! Matika.in: Stavby z kostek
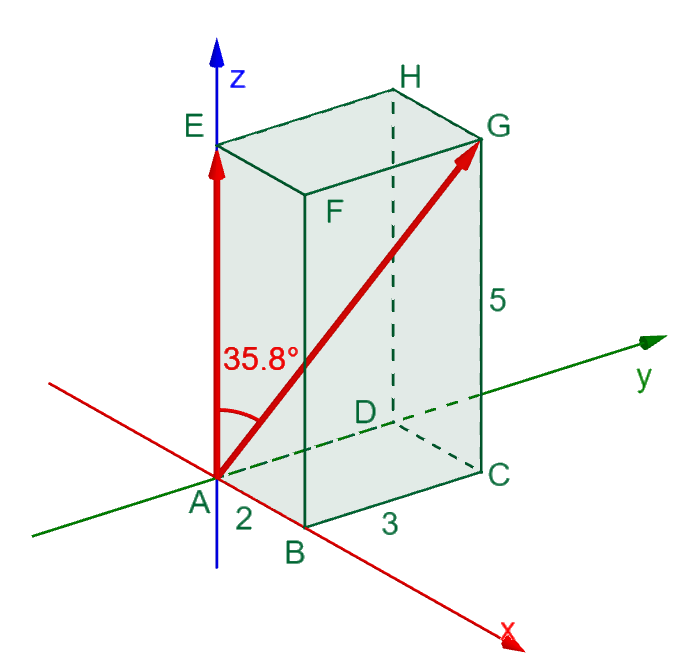
  Cvičení:	Skalární součin Kapitola 7.4 (str. 48) Zadání úkolu pro cvičení: Vypočítejte odchylku hrany a tělesové úhlopříčky kvádru o rozměrech 2 x 3 x 5, viz obrázek. [GeoGebra applet]

• Planimetrie. Symetrie roviny. Geometrická zobrazení. Shodnost v rovině.

  Přednáška:

  Kapitola 12         Symmetry in Geometry (Video) Geometrická zobrazení (v rovině) GeoGebra - Nákresna Kapitola 13 Shodná zobrazení

  Cvičení:

  Wikipedia: Symmetry [Osová souměrnost]   [Otočení]   [Středová souměrnost]   [Posunutí]   [Posunutá souměrnost] Úkol: Je dána přímka p a body A, B v téže polorovině s hraniční přímkou p. Najdete všechny body X ∈ p takové, že součet vzdáleností |AX| + |BX| je minimální. (Tato úloha je známa jako Heronův problém; Hérón Alexandrijský, přibl. 10-70 n.l.) Zadání úloh pro cvičení (Cvičení 9).   [Řešení cvičení 9] [Příklad 8 (Rotace rovnostranného trojúhelníku)]   [Příklad 9 (Zobrazení reprodukující rovnostranný trojúhelník)]   [Příklad 10 (Obdélník a jeho obraz v otočení)]

• Osová souměrnost. Osově souměrné útvary. Středová souměrnost. Středově souměrné útvary.

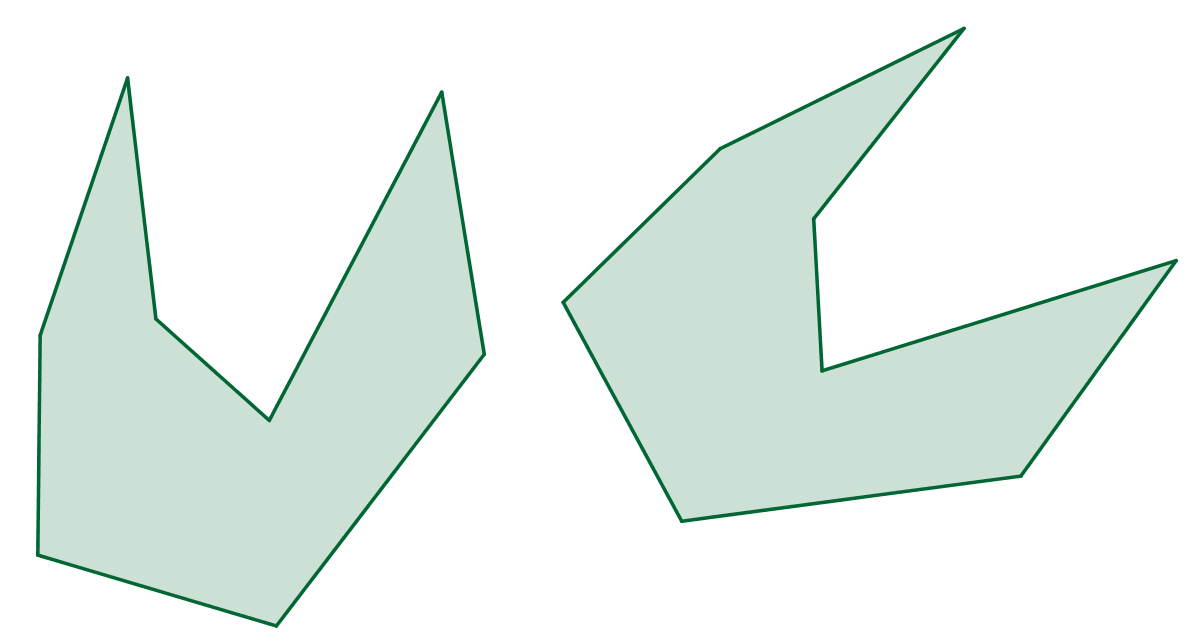
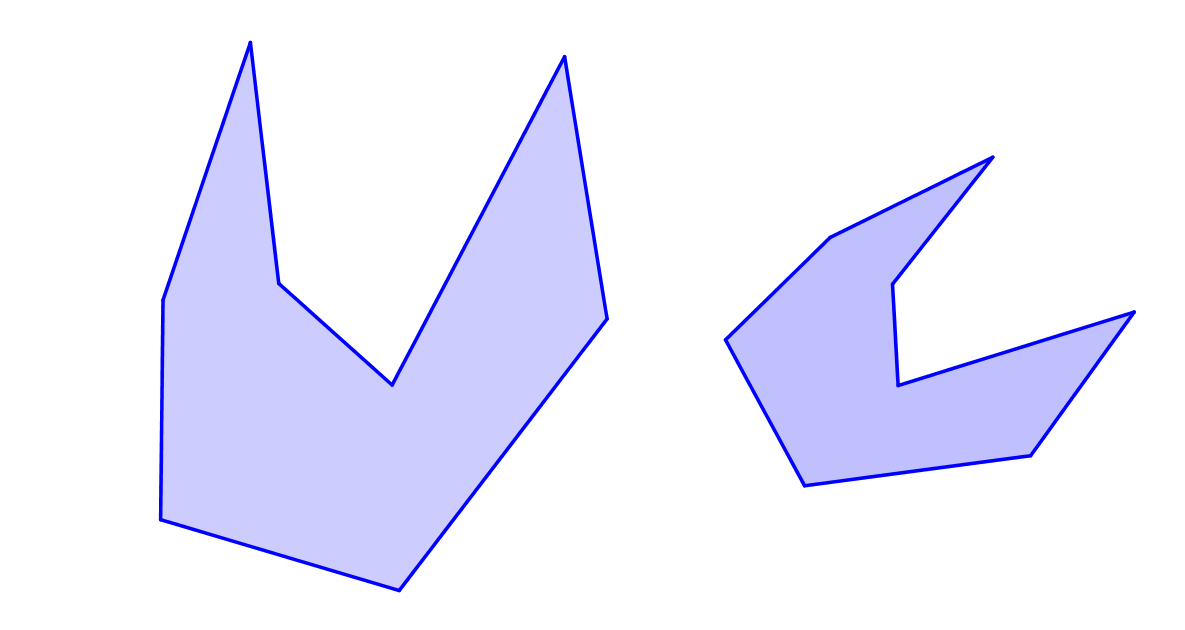
  Přednáška:	Kapitola 13 Které z dvojic útvarů jsou vzájemně shodné či podobné?   Shepard's tables   GeoGebra - Nákresna
  Cvičení:	Zadání úloh pro cvičení (Cvičení 10). Řešení cvičení 10 (GeoGebra applety): [Příklad 1] [Příklad 2] [Příklad 3] [Příklad 4] [Příklad 5] [Příklad 6]

• Posunutí. Otočení. Posunuté zrcadlení.
• Skládání geometrických zobrazení.

  Přednáška:	Kapitola 13 Složení dvou osových souměrností, jejichž osy jsou na sebe kolmé. 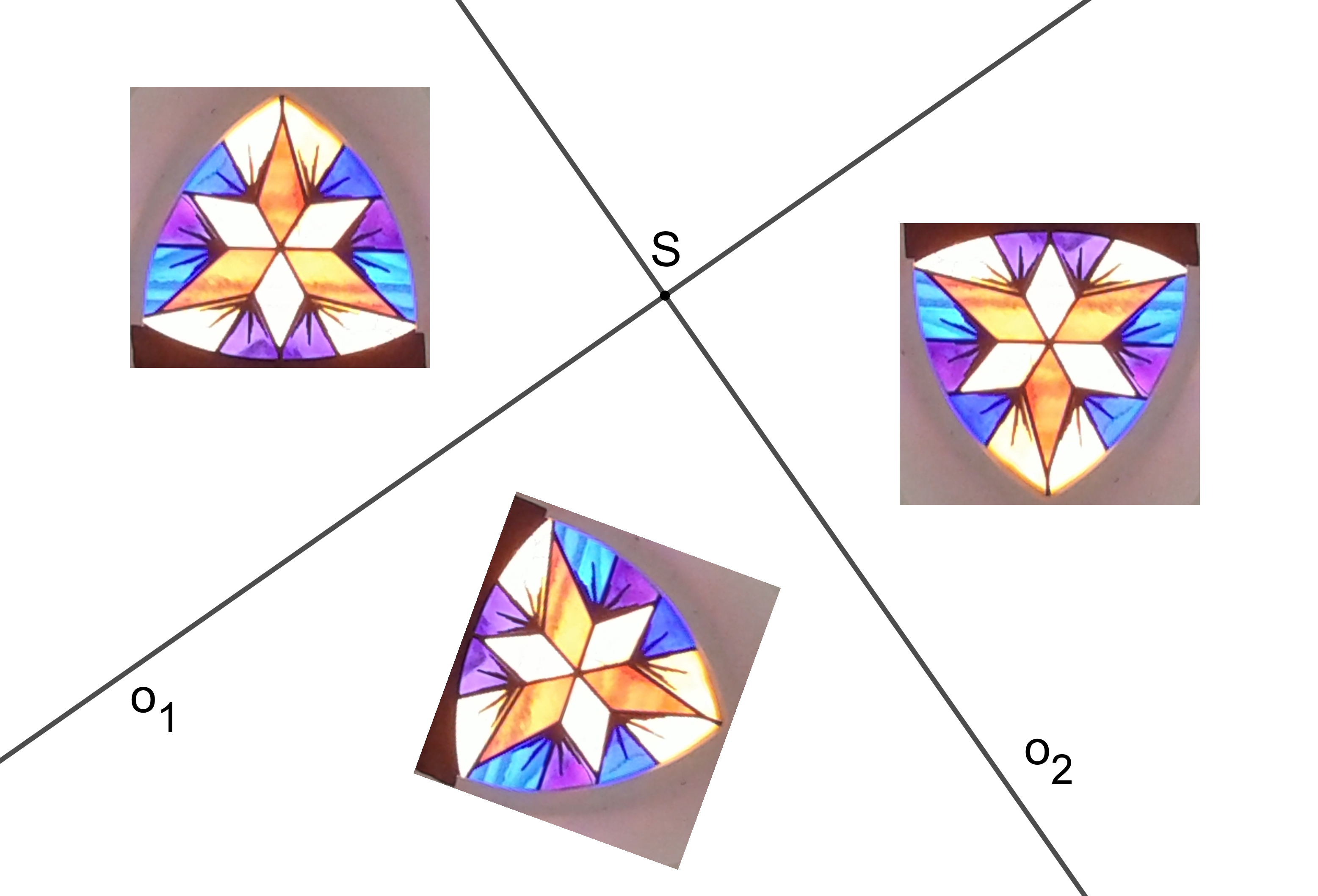[GeoGebra applet]
  Cvičení:

• Podobnost. Podobné zobrazení v rovině a v prostoru.

  Přednáška:

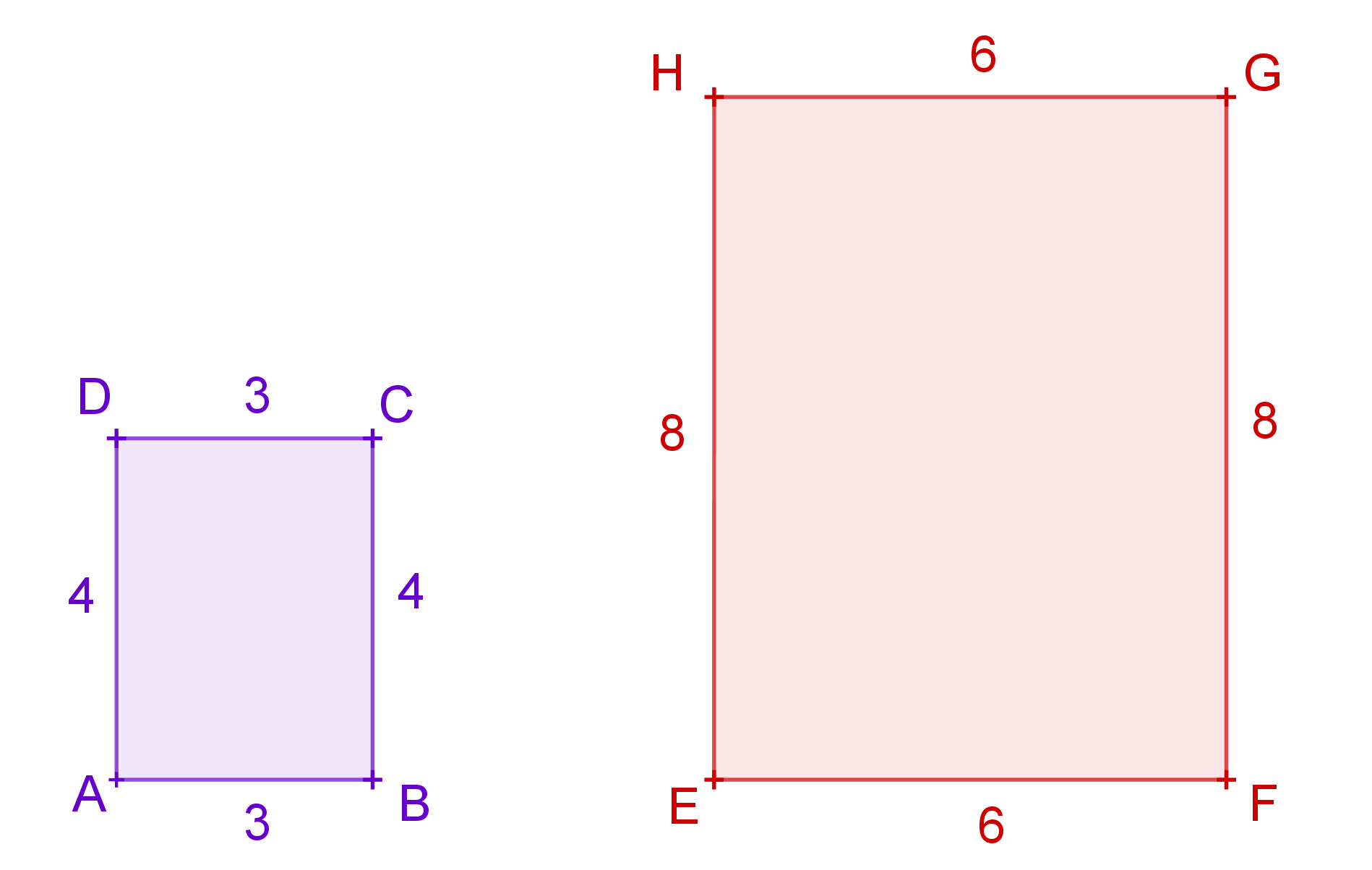
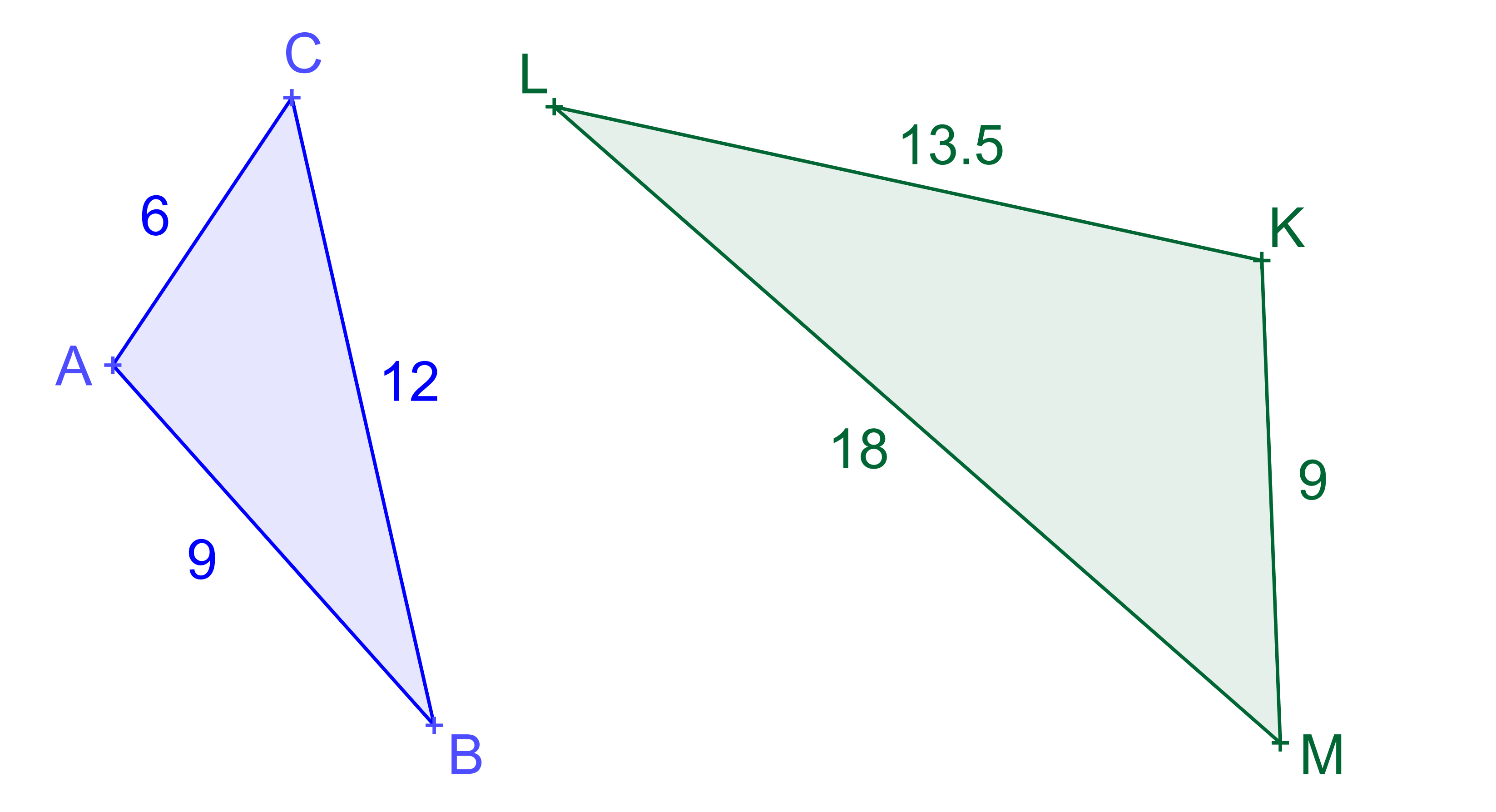
  Kapitola 14 Podobné útvary. ÚKOL: Zdůvodněte podobnost trojúhelníků na obrázku! 0,0 –o+←↓↑→ A B C A1 B1 C1

  Cvičení:

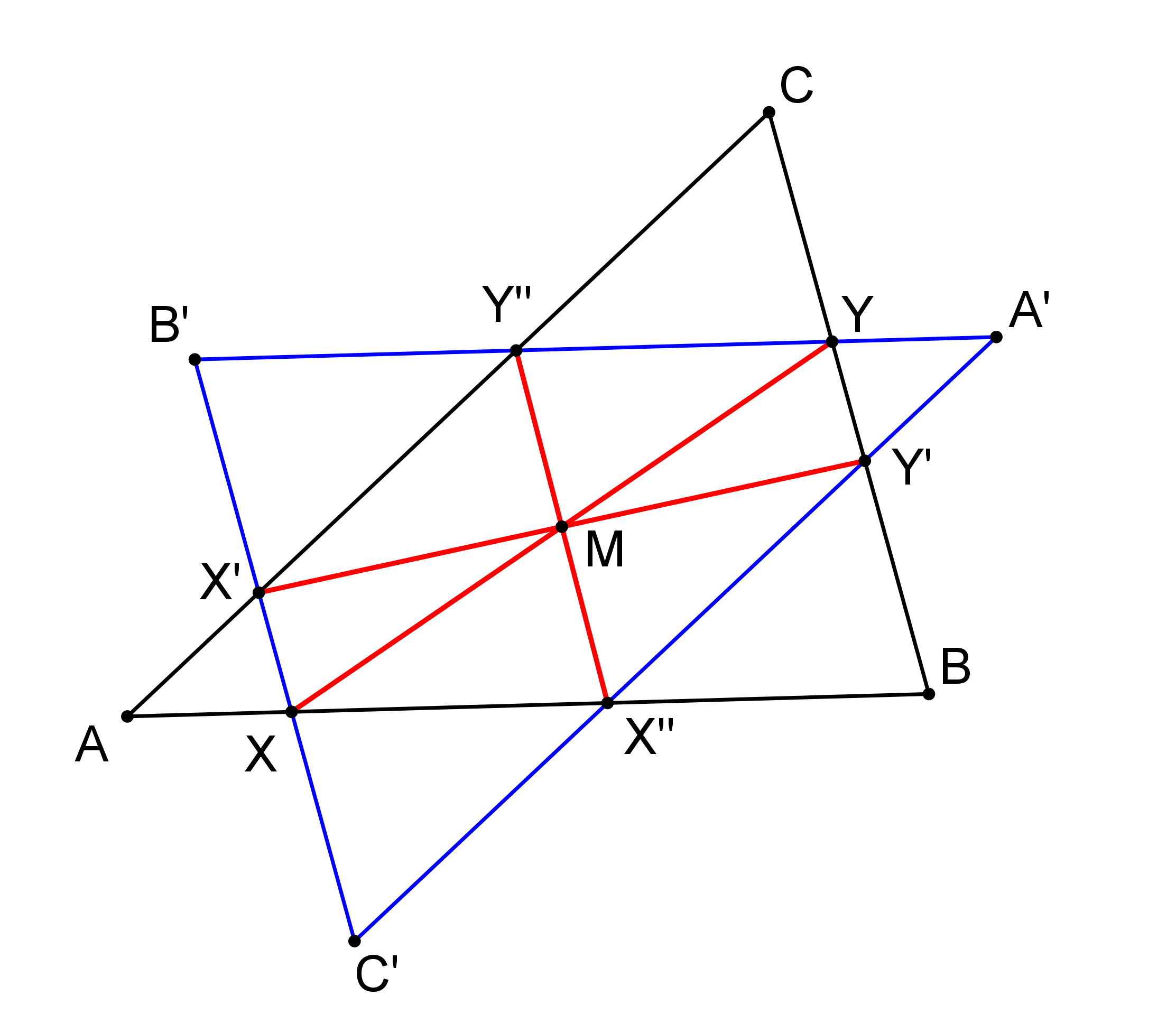
  PŘÍKLAD 13.3. Je dán trojúhelník ABC a jeho vnitřní bod M. Sestrojte všechny úsečky XY se středem M a s krajními body X, Y na hranici trojúhelníku. Řešení: [GeoGebra applet] Detailní popis řešení příkladu je uveden v textu Hašek, R. Planimetrie na str. 59. PŘÍKLAD 13.5. Jsou dány různé rovnoběžné přímky a, b, c a bod A, který leží na přímce a. Sestrojte všechny rovnostranné trojúhelníky ABC,jejichž vrcholy B, C leží po řadě na přímkách b, c. Řešení: GeoGebra applet PŘÍKLAD 14.5. Sestrojte alespoň jeden trojúhelník ABC, pro který platí |AB|:|AC| = 3:5, α = 60°, ρ = 1,8 cm (poloměr kružnice vepsané). Řešení: GeoGebra applet Detailní popis řešení příkladu je uveden v textu Hašek, R. Planimetrie na str. 104. PŘÍKLAD 14.6. Sestrojte kosodélník ABCD, je-li dáno |∠DAB| = α, |∠ABD| = ε, |AC| = e. Řešení: GeoGebra applet Detailní popis řešení příkladu je uveden v textu Hašek, R. Planimetrie na str. 105.

• Stejnolehlost kružnic. Věty o podobnosti trojúhelníků.

  Přednáška:

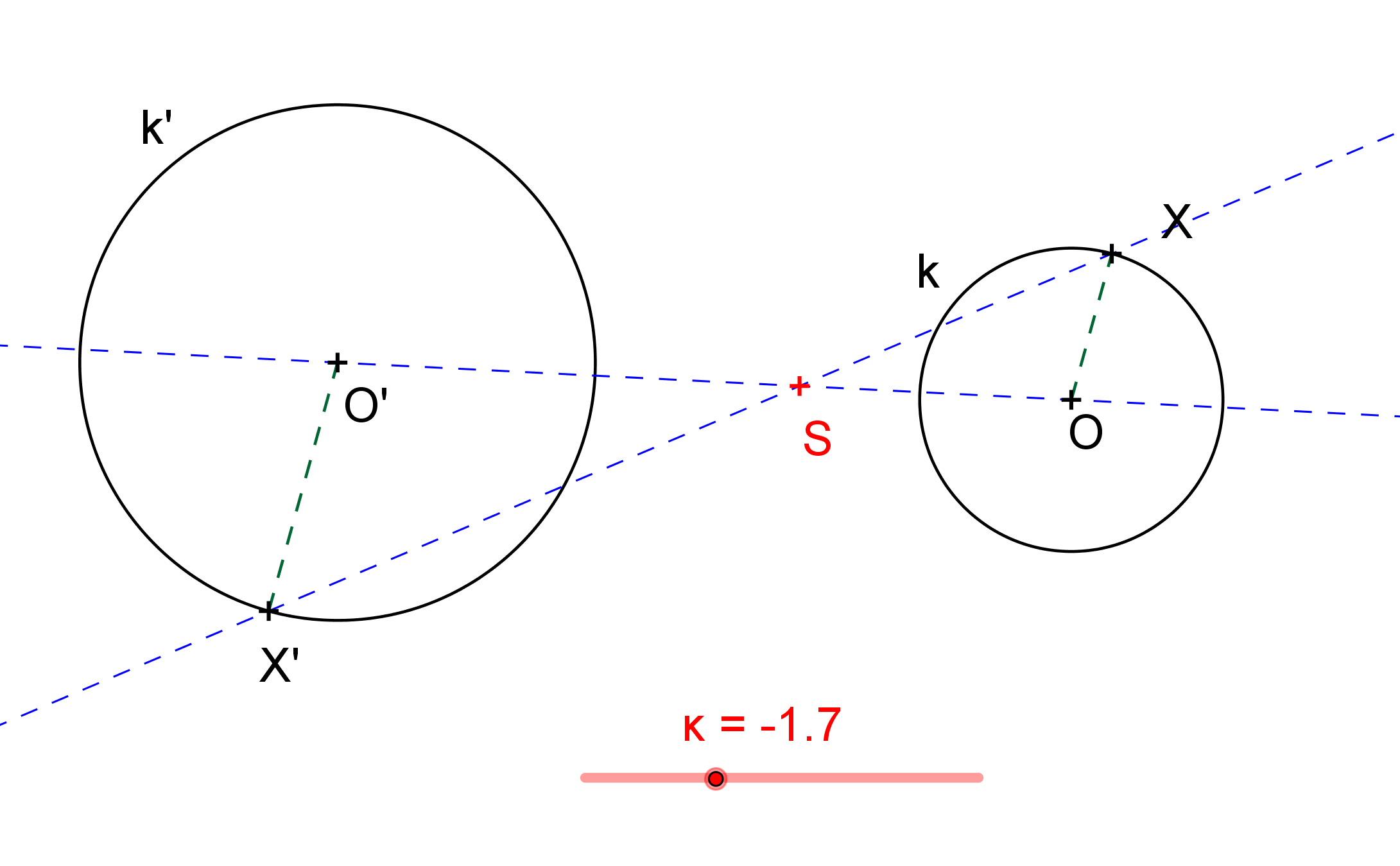
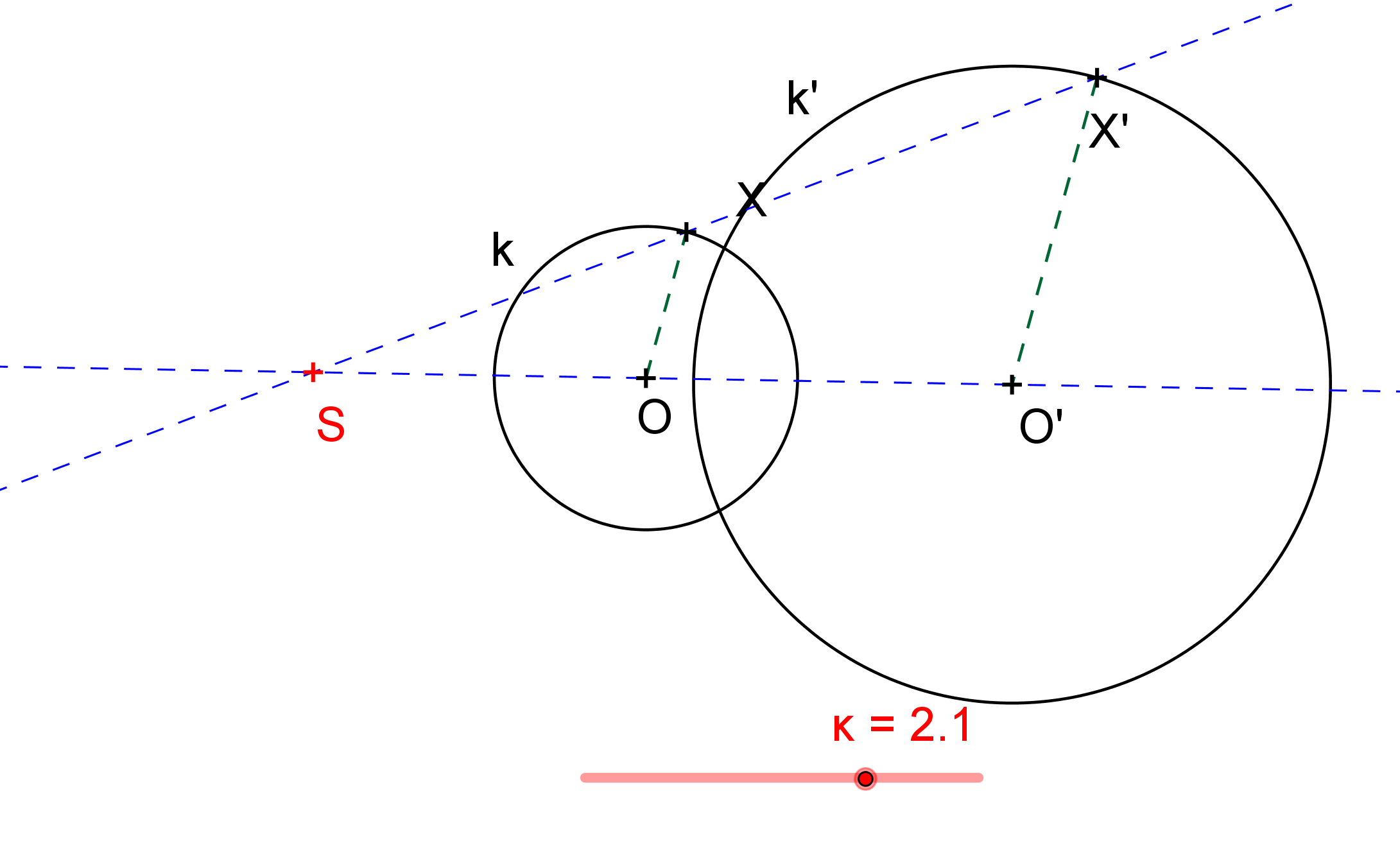
  Kapitola 15 - Stejnolehlost GeoGebra applet: Stejnolehlost Zobrazení kružnice ve stejnolehlosti   [GeoGebra applet: Zobrazení kružnice ve stejnolehlosti] Určení středů stejnolehlostí dvou kružnic Každé dvě kružnice jsou stejnolehlé; existují jedna, většinou však dvě stejnolehlosti, v nichž se jedna zobrazí na druhou. Zajímá nás, jak určíme středy těchto stejnolehlostí. Koeficenty jsou jasné, jejich absolutní hodnota je rovna poměru poloměrů příslušných kružnic, v pořadí obraz - vzor.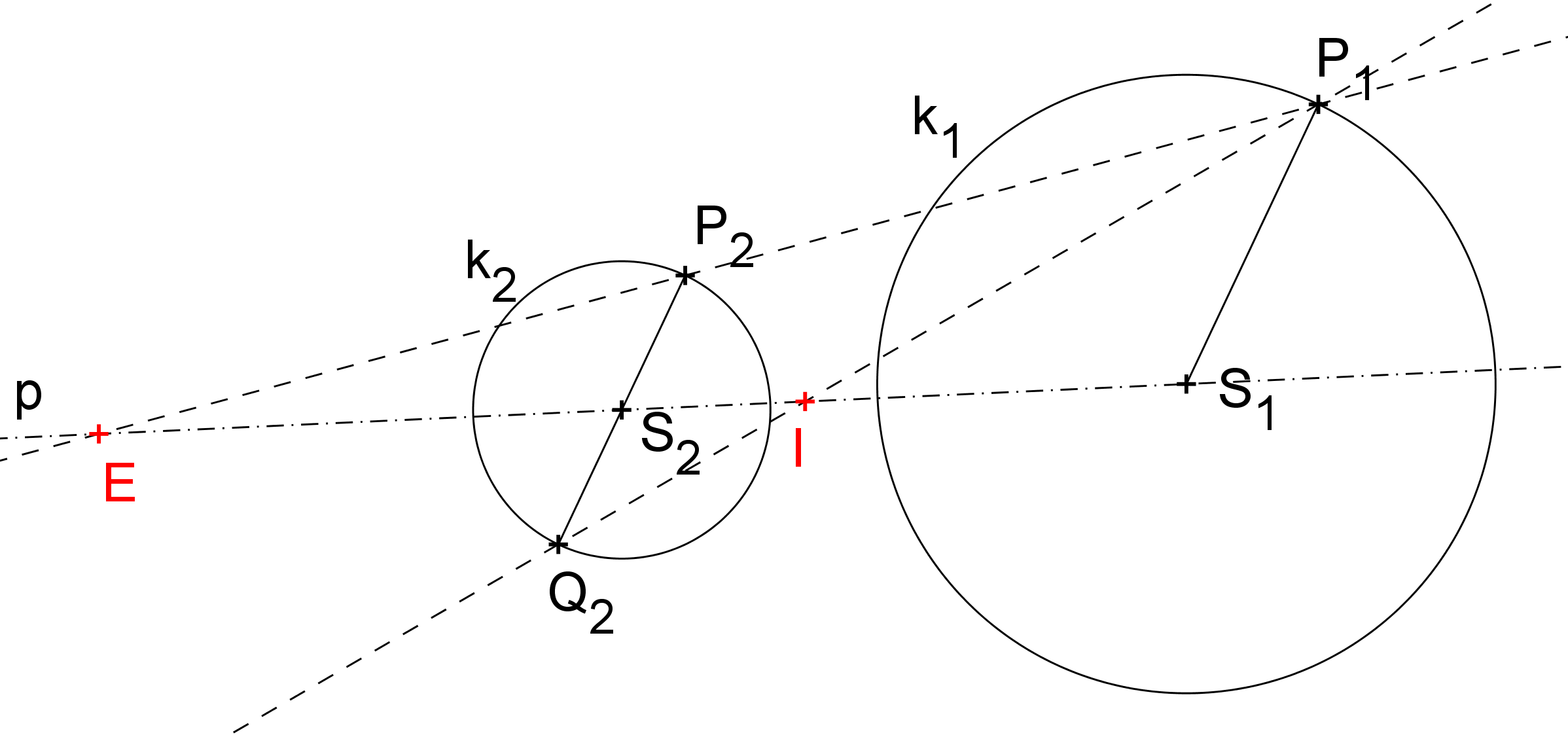 [GeoGebra applet: Určení středů stejnolehlostí dvou kružnic] Konstrukce společných tečen dvou kružnic Společné tečny kružnic procházejí středy jejich stejnolehlostí, vnější tečny středem E, vnitřní tečny středem I. Stačí tedy najít tyto středy a potom sestrojit tečny z každého z nich k jedné z daných kružnic (užitím Thaletovy kružnice), automaticky budou tečnami i druhé kružnice.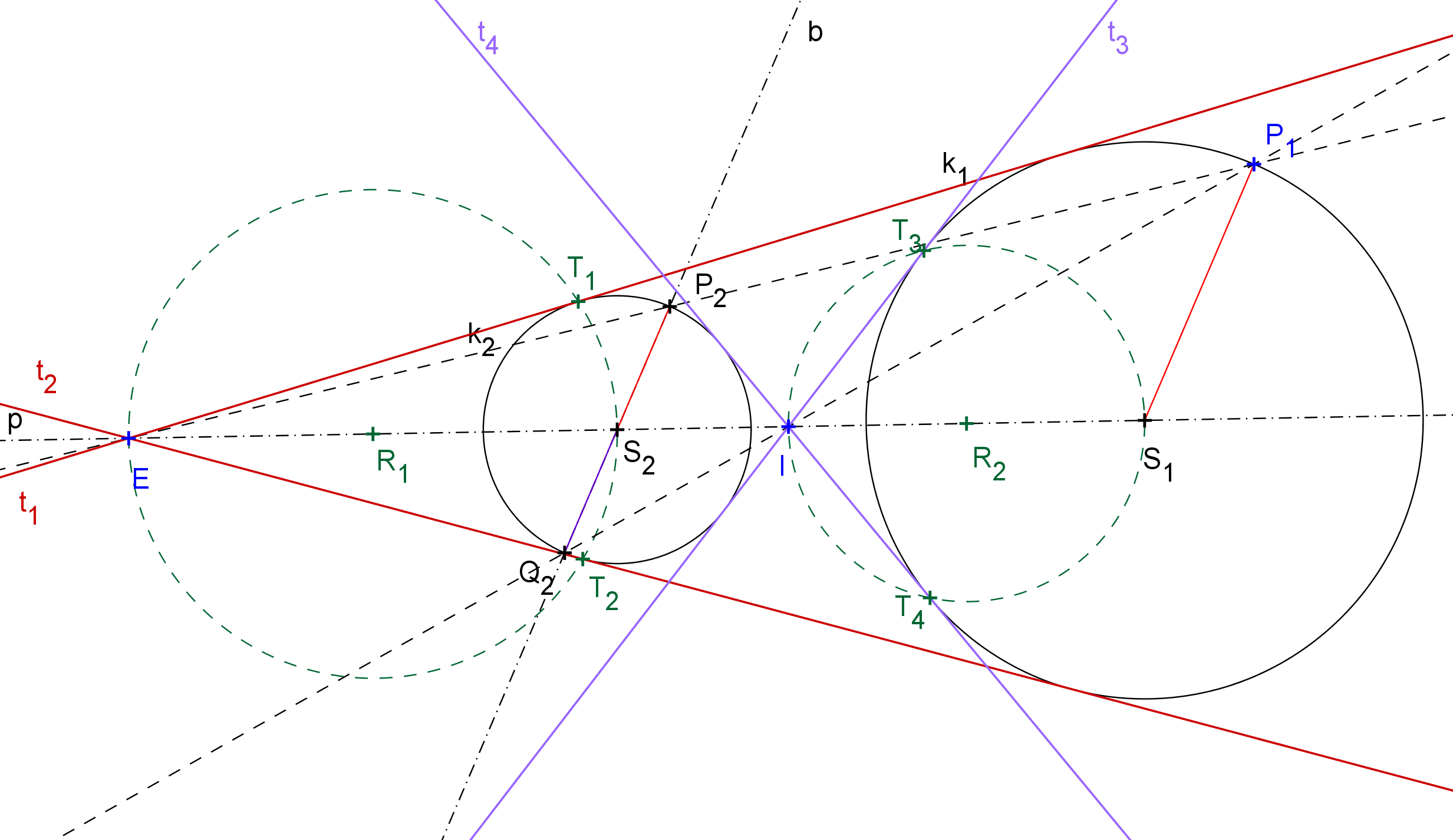 [GeoGebra applet: Konstrukce společných tečen dvou kružnic] Kapitola 14 - Podobnost Věty o shodnosti trojúhelníků sss, sus, usu, Ssu Věty o podobnosti trojúhelníků sss, sus, uu, Ssu       Proč nelze uvažovat shodu v úhlu proti menší ze stran? 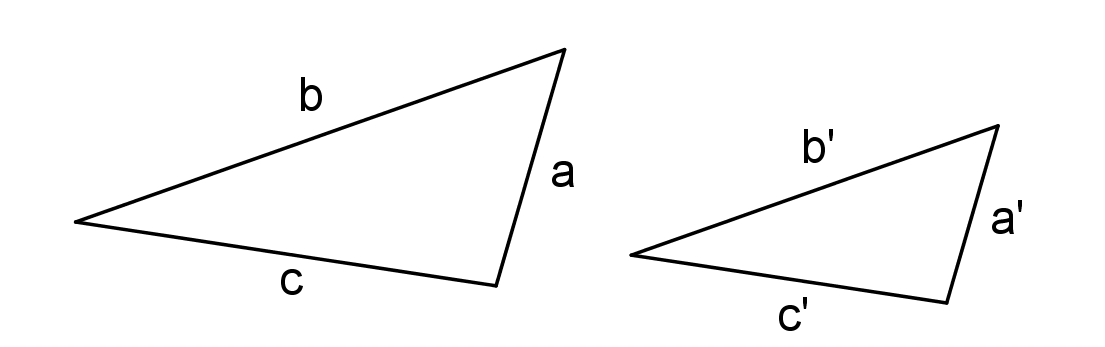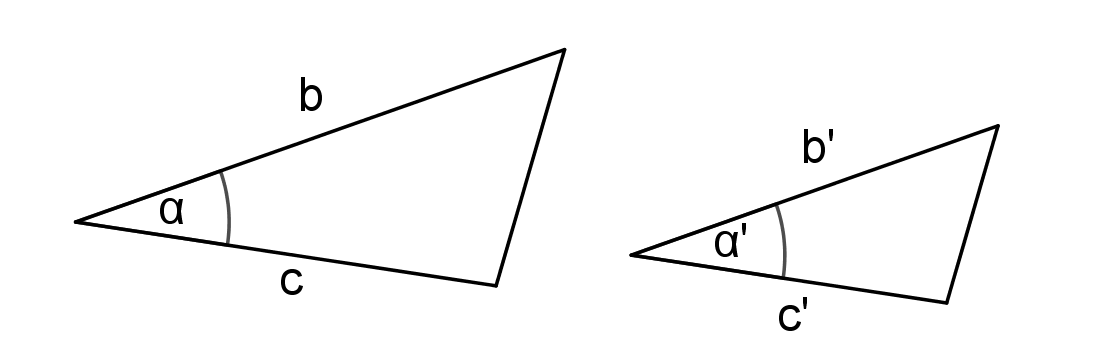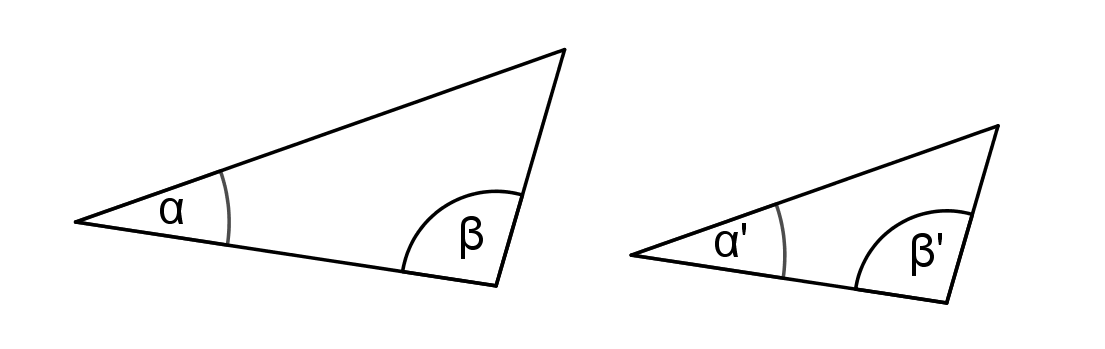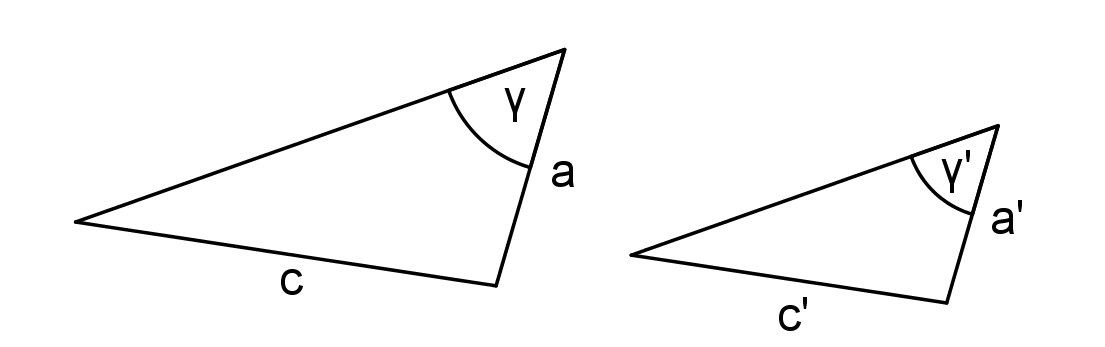Protože existují dva různé trojúhelníky, které se shodují ve dvou stranách a úhlu proti měnší z nich!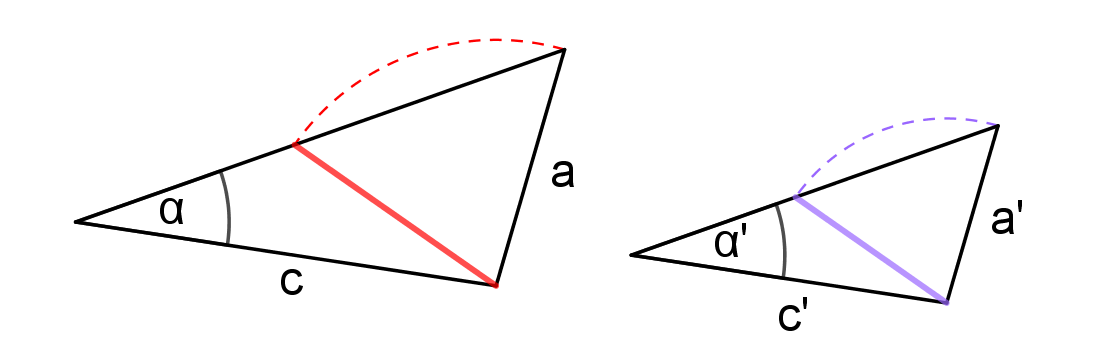

  Cvičení:

Materiály k přednáškám

[Eukleidovské konstrukce]
[Kosý šestiboký hranol (GeoGebra aplet)] [Kolmý pětiboký hranol (GeoGebra aplet)]
[Pravidelné mnohostěny (prezentace v pdf)]
[Cavalieriho princip (GeoGebra aplet)]
[Symmetry in Geometry (Video)]
[GeoGebra aplet: Stejnolehlost]
[Elica (volně dostupný soubor aplikací především pro podporu stereometrie)]
[Paper models of polyhedra: http://www.korthalsaltes.com]

Literatura

[1] Odvárko, O., Kadleček, J. Přehled matematiky pro ZŠ a víceletá gymnázia. Prometheus, Praha, 2004.
[2] Kuřina, F. 10 geometrických transformací. Prometheus, Praha, 2002.
[3] Kuřina, F. 10 pohledů na geometrii. Akademie věd České republiky, 1996.
[4] Polák, J. Přehled středoškolské matematiky. Prometheus, Praha.
[5] Pomykalová, E. Matematika pro gymnázia - Planimetrie. Prometheus, Praha, 2008.
[6] Pomykalová, E. Matematika pro gymnázia - Stereometrie. Prometheus, Praha, 2014.
[7] Jacobs, H. R. Geometry: seeing, doing, understanding. 3rd ed. New York: W.H. Freeman and Co., 2003.
[8] Voráčová a kol., Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha, 2012.
[9] Vyšín, J. a kol.: Geometrie pro pedagogické fakulty I. díl, SPN, Praha, 1965.
[10] Eukleides, Eukleidovy základy (Elementa), překlad F. Servít, 1907.
Dostupné na https://commons.wikimedia.org/wiki/File:Eukleides_Servit.pdf
[11] učebnice a sbírky úloh pro ZŠ a SŠ.
[12] Fuchs, E., Zelendová, E. Metodické komentáře ke Standardům pro základní vzdělávání: Vzdělávací obor Matematika a její aplikace. NÚV, 2015. [PDF], [https://clanky.rvp.cz/clanek/c/Z/20617/METODICKE-KOMENTARE-K-OBORU-MATEMATIKA-A-JEJI-APLIKACE.html/], str. 74-104.

Internetové odkazy

Software ke stažení

www.geogebra.org ... program GeoGebra (možnost bezplatného stažení)

Materiály pro výuku a sebevzdělávání

Wolfram Demonstrations Project
www.cut-the-knot.org (Interactive Mathematics Miscellany and Puzzles)
http://www.math.uoc.gr (Geometrikon - galerie geometrických témat)

Požadavky na studenta

• Zkouška.
  • Zkouška má dvě části - písemnou a ústní. Předmětem písemné zkoušky je řešení úloh odpovídajících úlohám probíraným na přednáškách a cvičeních. Ústní zkouška je zaměřena na ověření znalosti základních pojmů probíraných na přednáškách. Písemná část zkoušky je tvořena jednou písemnou prací (místo původně plánovaných dvou, jedná se o reakci na opatření proti covid-19), která se píše na konci semestru. Pro úspěšné absolvování písemné zkoušky, které je podmínkou pro konání ústní zkoušky, je vyžadována minimálně 50% úspěšnost. V případě neúspěchu může student/studentka opakovat písemnou část zkoušky při svém prvním - řádném termínu zkoušky z předmětu KMA/8M1, na který se zapíše. Každý má nárok na jeden řádný termín a dva opravné.
    [Otázky ke zkoušce KMA/8M1 2020]