Matematika a její aplikace (KPE/PMAR) - GEOMETRIE (R. Hašek) |
UPOZORNĚNÍ: Předmět KPE/PMAR: Matematika a její aplikace je zaměřen na celé učivo matematiky na 1. stupni základní školy. Tato webová stránka ale slouží jako opora pouze pro tu část předmětu, která je věnována tematickému okruhu Geometrie v rovině a v prostoru a která je vyučována Mgr. Romanem Haškem, Ph.D. (viz tučně vyznačená část níže uvedeného obsahu předmětu). Příprava na výuku ostatních tematických okruhů je v rámci tohoto předmětu vedena RNDr. Marikou Hrubešovou, Ph.D. a RNDr. Janou Vysokou, Ph.D.
Obsah předmětu KPE/PMAR
viz STAG: KPE/PMAR | Rozvrh D
Pojem číslo a algebra (vytváření pojmu přirozené číslo, metody porovnávání čísel, rovnost, nerovnost, metodické prostředky numerace, rozdělení číselných oborů a rozšiřování číselného oboru, vyjádření přirozeného čísla v numerační soustavě, výklad podstaty základních aritmetických operací, nácvik spojů - metodika nácviku násobilky a "sčítalky", vlastnosti početních operací v množině přirozených čísel a jejich reprezentace; možnosti modelování číselných vztahů; - pre-algebraické myšlení - rovnice a nerovnice; algoritmizované postupy písemného počítání Práce s daty - jednoduché grafy, používání kalkulátorů.
Tvar a prostor - interpretace geometrických pojmů vhodná pro děti 6 - 11leté, alternativní geometrie, metody práce v geometrii.
Měření - teoretické základy měření, přehled jednotek měření používaných ve škole, praktické provádění měření.
Shodnost v geometrii, shodná zobrazení.
Úlohy rozvíjející funkční myšlení. Činnosti v matematice: řešení slovních úloh, řešení problémů, úlohy s otevřeným koncem, hry. Budou také probírána obecnější témata, která souvisí s matematickým vzděláváním na prvním stupni základního vzdělávání: cíle, jazyk, hodnocení a klasifikace, řízení třídy, péče o talentované žáky.
Cíle výuky geometrie na 1. stupni ZŠ
|
Obsah tematického okruhu Geometrie v rovně a v prostoru
|
Očekávané výstupy
|
Studijní opory
-
Předmatematické zkušenosti z MŠ
- Samková, L. Získávání předmatematických zkušeností v mateřské škole. South Bohemia Mathematical Letters, Volume 22 (2014), No. 1, 38-42. [http://home.pf.jcu.cz/~lsamkova/kipk/sbml.pdf]
- Samková, L. Náměty pro formování předmatematických zkušeností (prezentace). [http://home.pf.jcu.cz/~lsamkova/kipk/Konzultace1.pps]
-
Kurz Moodle k předmětu KPE/PMAR
- Hošpesová, A. Matematika a její aplikace. [https://moodle.pf.jcu.cz/enrol/index.php?id=330]
-
Geometrie v rovině a v prostoru na 1. stupni ZŠ
- Fuchs, E., Zelendová, E. Metodické komentáře ke Standardům pro základní vzdělávání: Vzdělávací obor Matematika a její aplikace. NÚV, 2015. [PDF], [https://clanky.rvp.cz/clanek/c/Z/20617/METODICKE-KOMENTARE-K-OBORU-MATEMATIKA-A-JEJI-APLIKACE.html/], str. 74-104.
-
Didaktická literatura
- Hejný, M., Kuřina, F. Dítě, škola a matematika; Konstruktivistické přístupy k vyučování. Praha: Portál, 2. aktualizované vydání, 2009, 2015. [https://obchod.portal.cz/pedagogika/dite-skola-a-matematika]
-
Vondrová, N., Rendl, M. a kol. Kritická místa matematiky na základní škole očima učitelů. Praha: Pedagogická fakulta, 1. vydání, 2013. Dostupné z: https://www.researchgate.net/publication/308959439_Kriticka_mista_matematiky_na_zakladni_skole_ocima_ucitelu
(Recenze od Františka Kuřiny, viz https://pages.pedf.cuni.cz/pedagogika/?p=11124&lang=cs) - Vondrová, N., Rendl, M. a kol. Kritická místa matematiky základní školy v řešení žáků. Praha: Karolinum, 1. vydání, 2016. [https://karolinum.cz/knihy/vondrova-kriticka-mista-matematiky-zakladni-skoly-v-reseni-zaku-15934]
-
Přehled učiva
- Odvárko, O., Kadleček, J. Přehled matematiky pro ZŠ a víceletá gymnázia. Prometheus, Praha, 2004. [https://prometheus-nakl.cz/index.php?zobraz=detail&id_katalog=63]
-
Základy geometrie pro studium učitelství 1. a 2. stupně ZŠ
-
Matematika I – Geometrie (KMA/8M1) (2020)
- www stránka: http://home.pf.jcu.cz/~hasek/8M1_2020.htm
- studijní text: Hašek, R. Úvod do geometrie. 2019
-
Planimetrie (KMA/PLA) (2020)
- www stránka: http://home.pf.jcu.cz/~hasek/PLA_2020.htm
- studijní text: Hašek, R. Planimetrie. 2020
-
Matematika I – Geometrie (KMA/8M1) (2020)
OBSAH PŘEDMĚTU
Tvar a prostor
-
Teoretická východiska výuky geometrie
-
Čtyři principy geometrie založené na zkušenosti (didaktická struktura geometrie) dle Františka Kuřiny (str. 1).
Kuřina, F. (2009) Didaktická transformace obsahu a školská praxe. Pedagogika Praha: PedF UK, 3/2009 (str. 298-308). Dostupné z: https://pages.pedf.cuni.cz/pedagogika/?attachment_id=999&edmc=999
-
Pět van Hieleho úrovní chápání geometrického učiva (str. 2).
Van Hiele model.
Wikipedia. Dostupné z: https://en.wikipedia.org/wiki/Van_Hiele_modelBudínová, I. (2018) Vědí žáci, co je čtverec? [online] In: Česká škola. Dostupné z: http://www.ceskaskola.cz/2018/01/irena-budinova-vedi-zaci-co-je-ctverec.html
Hra SOVA (tříbení si geometrických pojmů a geometrických vlastností vybraných těles)
-
Čtyři principy geometrie založené na zkušenosti (didaktická struktura geometrie) dle Františka Kuřiny (str. 1).
-
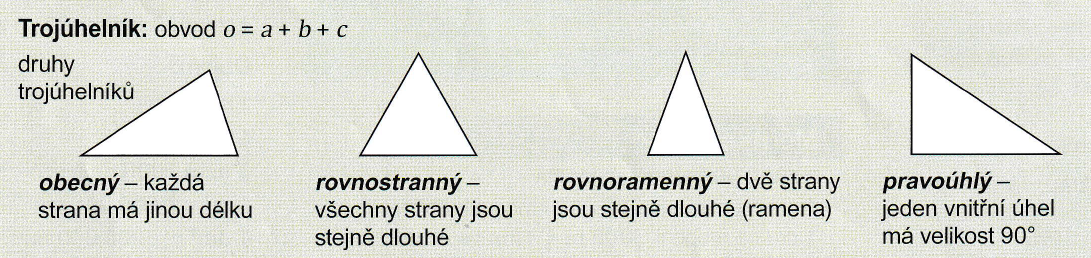
Trojúhelník. Mnohoúhelníky a ostatní rovinné útvary.
-
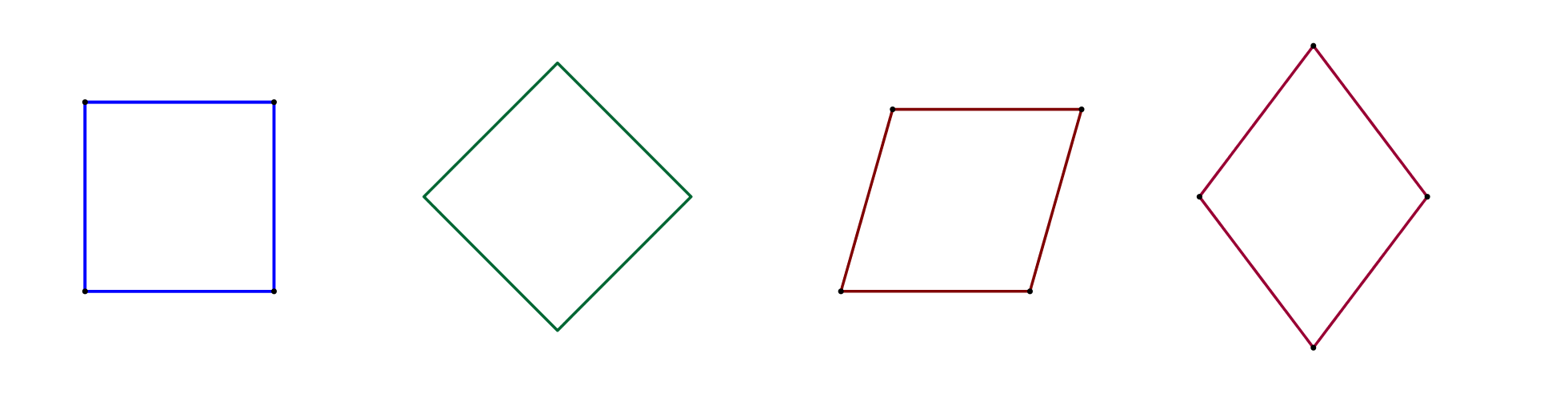
O jakých vlastnostech trojúhelníku/čtyřúhelníku vypovídají uvedené obrázky?







Trojúhelník je dán jednozačně délkami svých stran (sss).
-
Věty o shodnosti trojúhelníků
sss, sus, usu, Ssu
-
Věty o podobnosti trojúhelníků
sss, sus, uu, Ssu
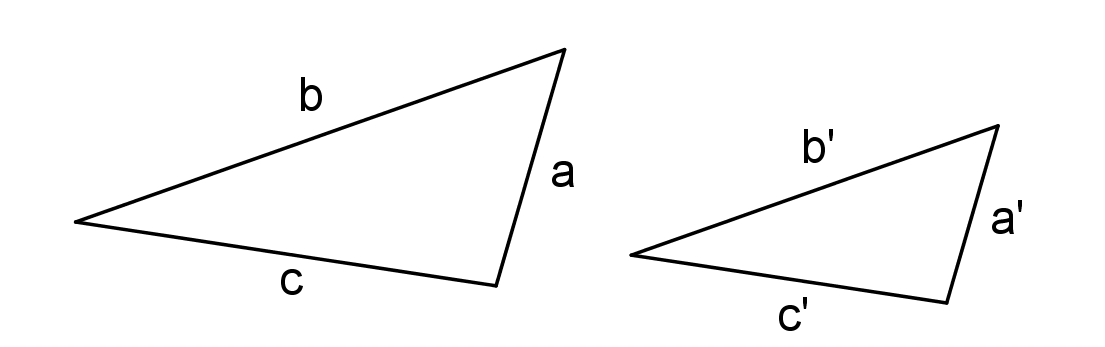
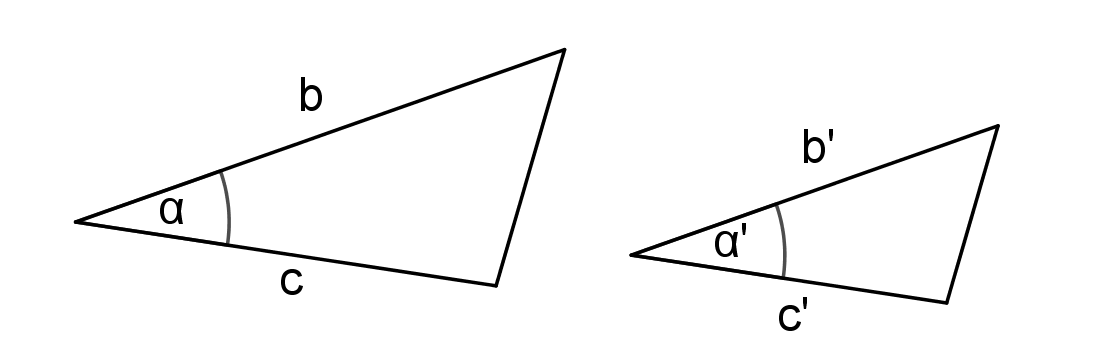
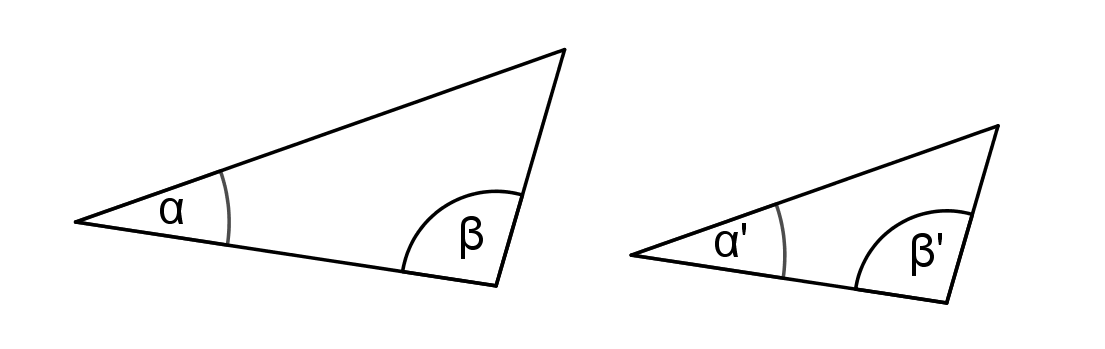
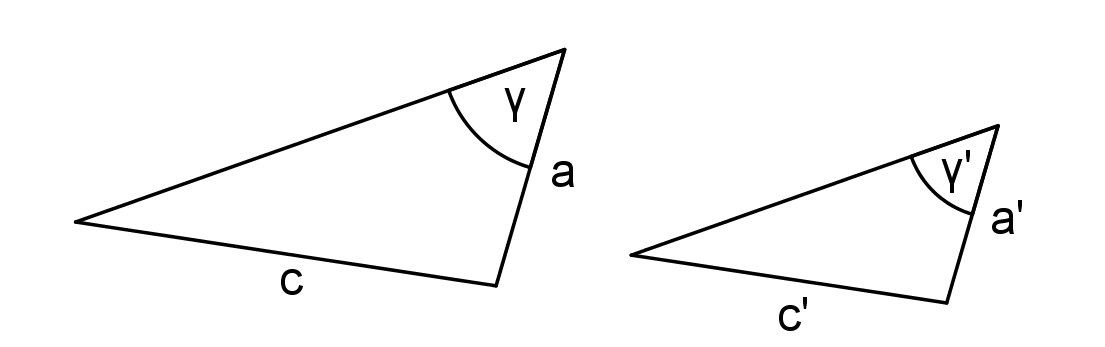
Protože existují dva různé trojúhelníky, které se shodují ve dvou stranách a úhlu proti měnší z nich!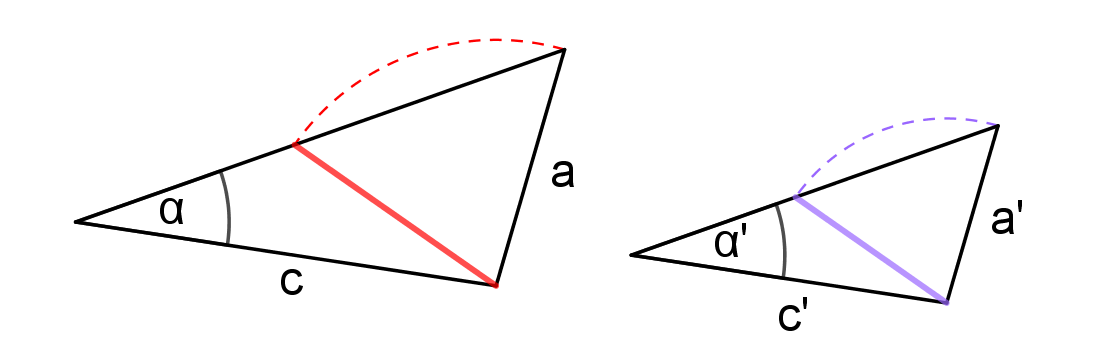
-
Věty o shodnosti trojúhelníků
-
K čemu Vás inspirují tyto obrázky?




- Euclidean tilings by convex regular polygons
-
Pokrytí roviny pravidelnými mnohoúhelníky
Zajímá nás, kterými pravidelnými mnohoúhelníky (vždy jenom jedním druhem a velikostí) můžeme pokrýt rovinu.




- GeoGebra - Nákresna
-
Platonská tělesa (pravidelné mnohostěny)

-
Tangram. Na co se můžeme ptát?


ÚKOL: Dle uvedeného obrázku si vyrobte Tangram (pokud tento hlavolam již nevlastníte) a pokuste se, užitím všech jeho součástí, jak stanoví pravidla, vytvořit co nejvíce různých konvexních n-úhelníků. Nafoťte nebo nakreslete.
-
Trojúhelníky (LN: Matematika pro páťáky) / prototypy
-
Popište obrázek. Co je na něm zachyceno?

Google Maps: Kansas
-
O jakých vlastnostech trojúhelníku/čtyřúhelníku vypovídají uvedené obrázky?
-
Čtvercová síť
-
Cvičení 1: Vypočítejte obsahy uvedených obrazců.
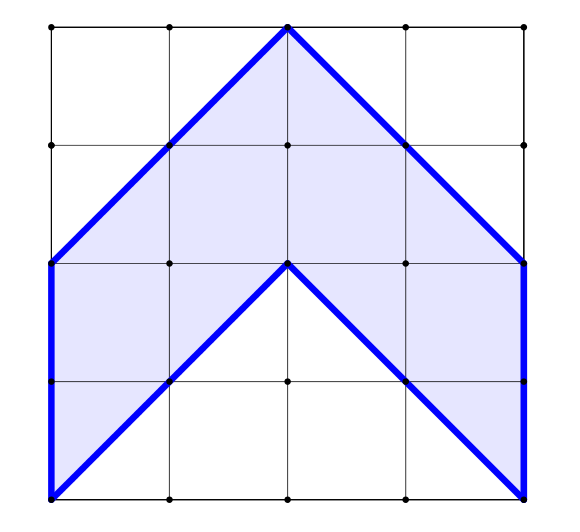
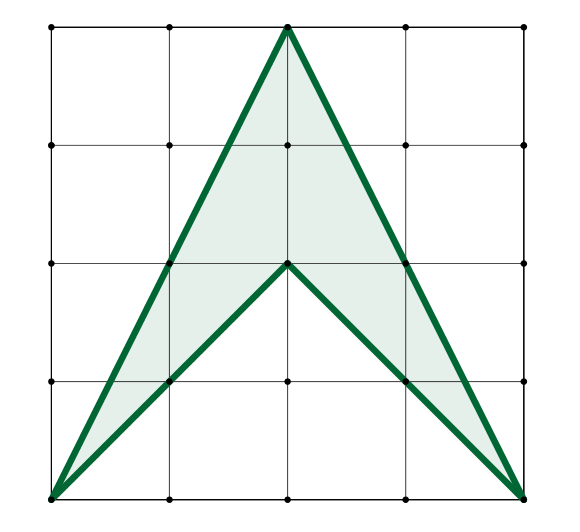
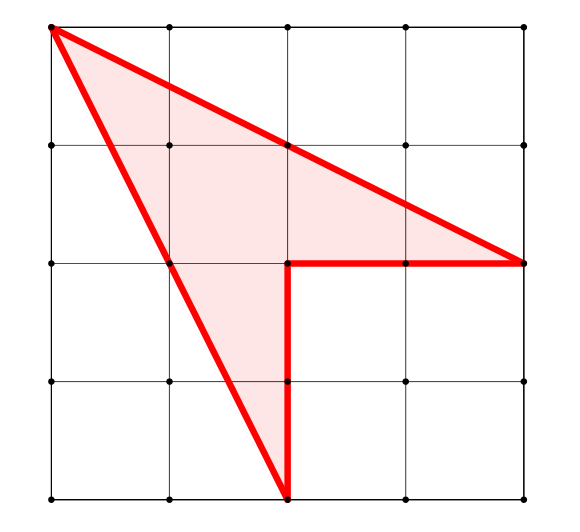
Cvičení 2: Vypočítejte obsahy obrazců dle zadání: Ukol_ctvercova_sit_2022.pdf.
Literatura pro další studium: Jordánová, D. Obsah a obvod obrazce s využitím čtvercové sítě ve výuce geometrie na 1. stupni ZŠ. Závěrečná práce DVPP - Učitelství pro 1. stupeň ZŠ. České Budějovice: Jihočeská univerzita v Č. B. 2020.
-
-
Geoboard
Procvičení výpočtu obsahu ve čtvercové síti: Ukol_ctvercova_sit_2022.pdf
ÚKOL: Kolik různých trojúhelníků (všechny vzájemně shodné uvažujeme jako jeden) můžeme vytvořit na geoboardu 3x3? Umíte je všechny pojmenovat (tj. použít pojmy pravoúhlý, rovnoramenný, tupoúhlý, ...)? Umíte u všech určit obsah (pokud předpokládáme, že vzdálenost sousedních kolíků desky je 1)? Zkuste to! Trojúhelníky nakreslete a opatřete výpočty obsahů. Více o geoboardu viz např. https://en.wikipedia.org/wiki/Geoboard.
-
Jordanova-Peanova míra
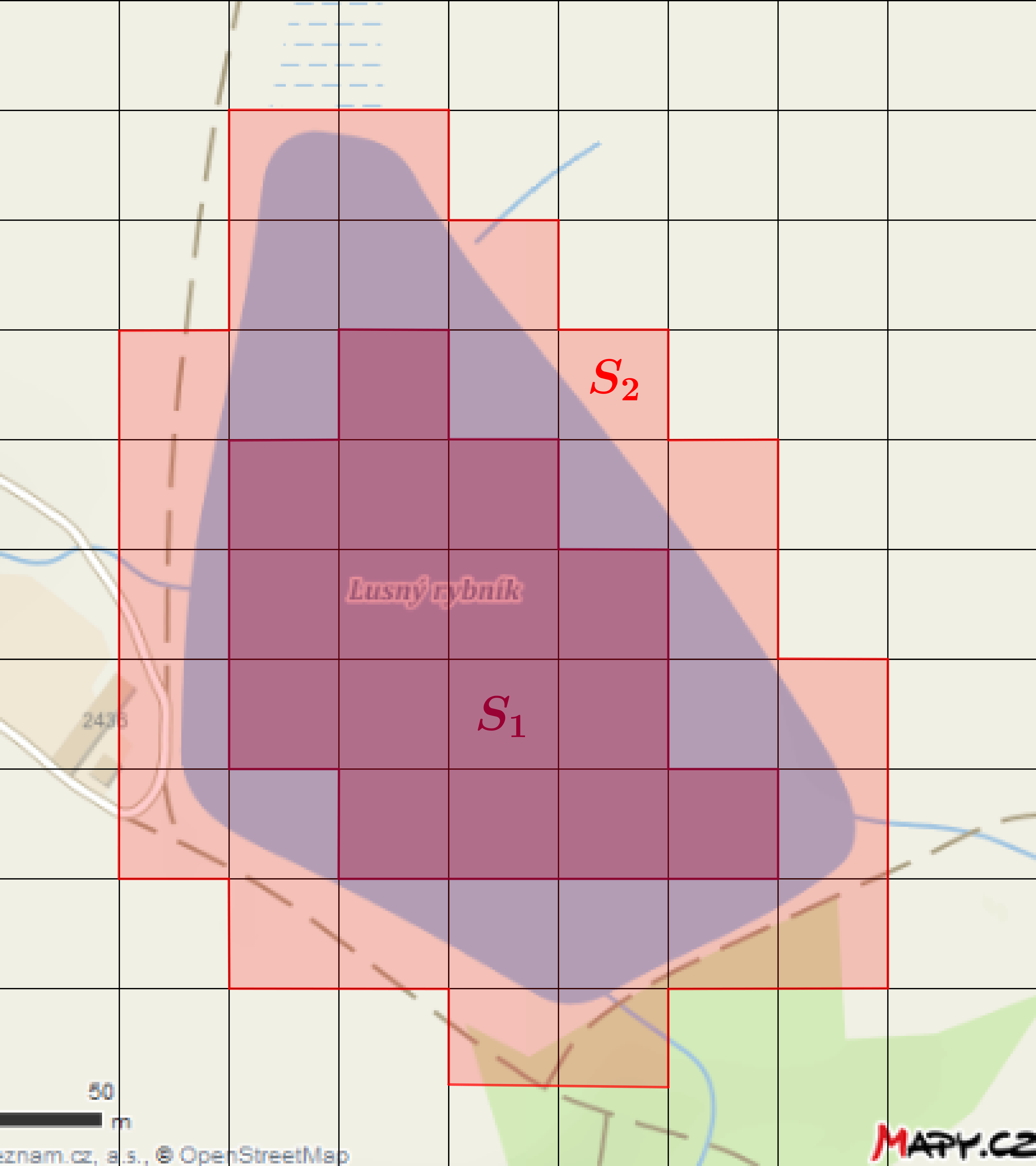
Rybník Lusný (Mapy.cz) -
Měření
Archimedův axiom: Pro libovolná dvě kladná čísla a, b existuje přirozené číslo n takové, že na>b. (Archimedean property )
Koeficient délkové / plošné / objemové změny.
-
Důkazy
Součet vnitřních úhlů v trojúhelníku / čtyřúhelníku. Obsah obdélníku / rovnoběžníku / trojúhelníku / lichoběžníku. Pythagorova věta. Thaletova věta.
-
Symetrie. Shodná zobrazení.
-
Co Vás zaujme na uvedených obrázcích? Popište tyto jevy.







Objekt, motiv či jev je symetrický, pokud existuje transformace (která není identitou), po jejímž uplatnění zůstane totožný sám se sebou (vizuálně nezměněn, případně zmenšený či zvětšený). Též můžeme říci, že daný objekt je vůči příslušné transformaci invariantní.
-
Najděte co nejvíce rovinných transformací popisujících vztahy mezi konkrétními dvojicemi dlaždic. Vypočítejte vnitřní úhly n-úhelníků tvořících dlaždice.

-
Co Vás zaujme na uvedených obrázcích? Popište tyto jevy.
-
Podobné zobrazení. Podobnost.
-
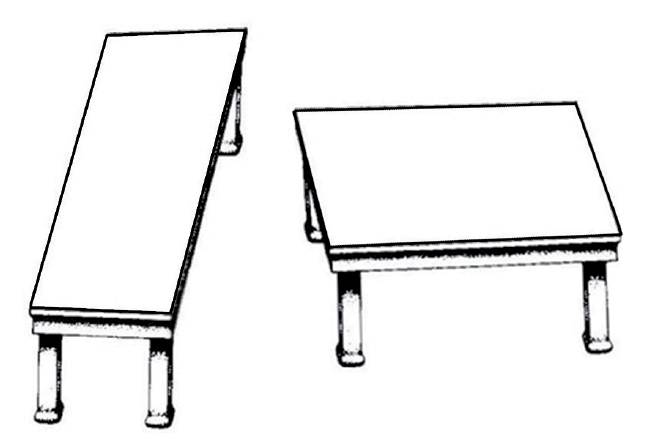
Jaké geometrické vztahy můžeme objevit na těchto obrázcích?


-
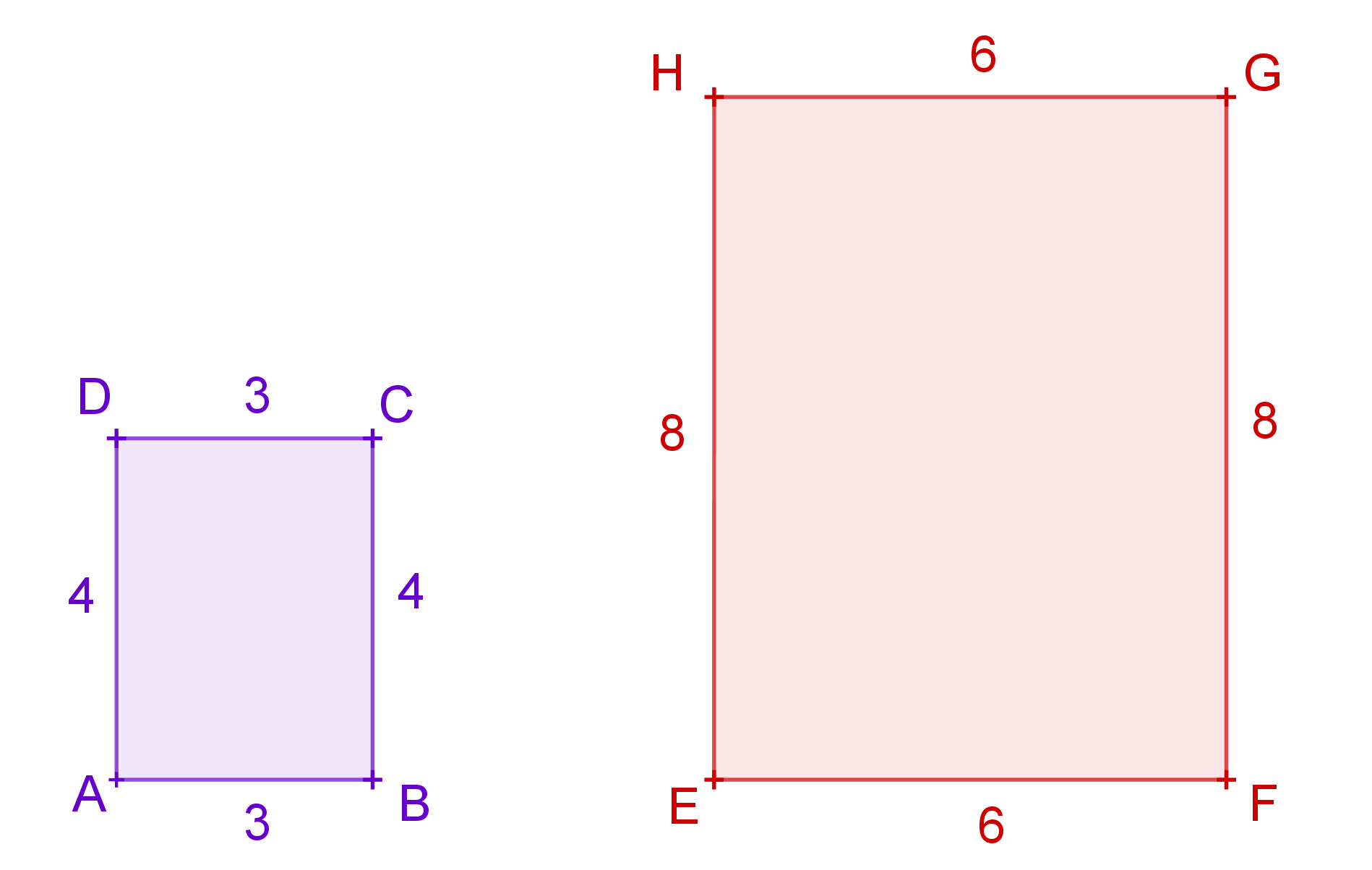
b>Které z dvojic útvarů jsou vzájemně shodné či podobné?
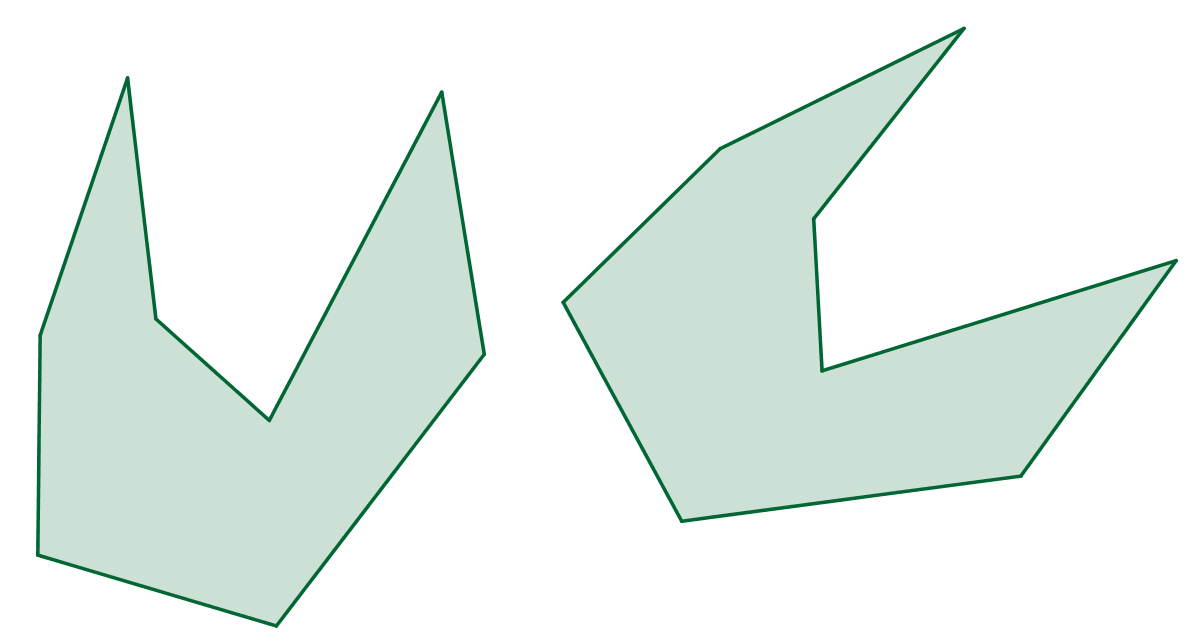
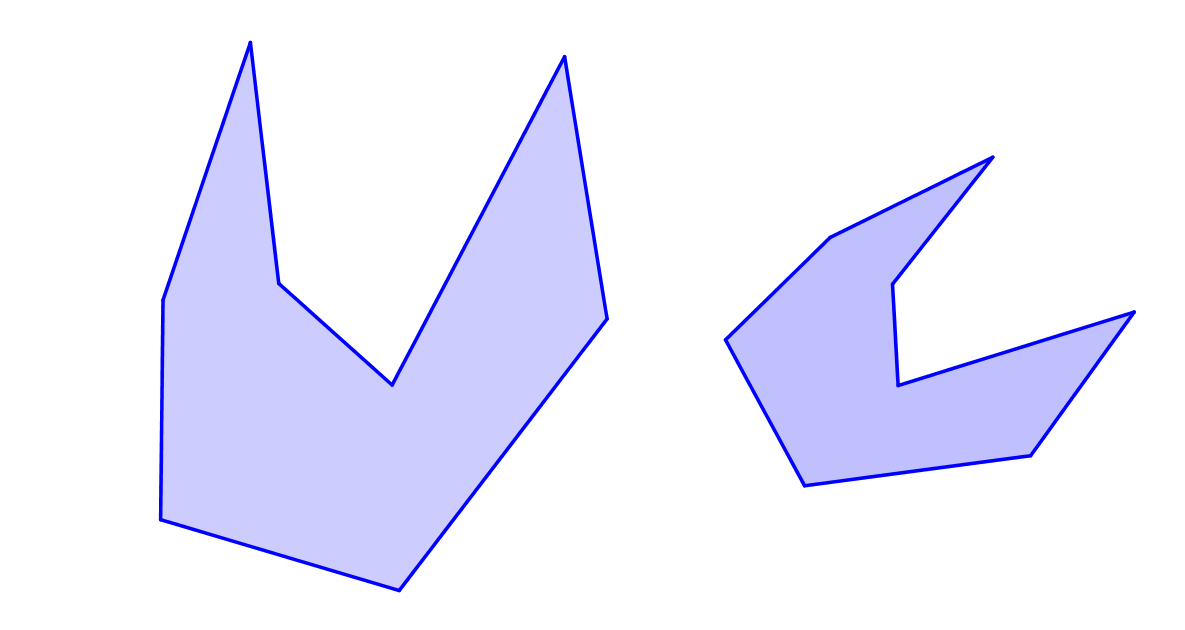
Shepard's tables -
Podobné útvary.
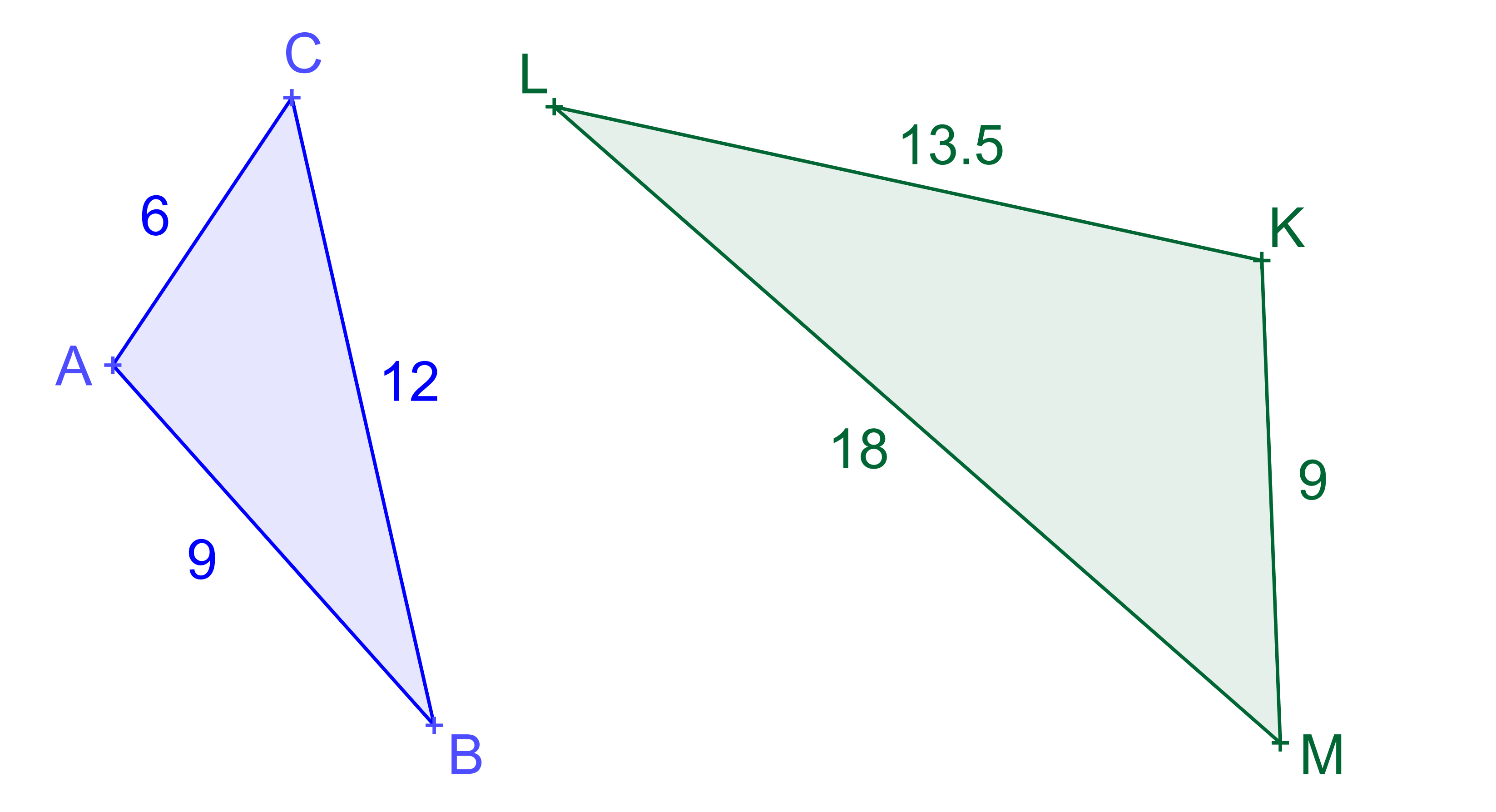
ÚKOL: Zdůvodněte podobnost trojúhelníků na obrázku!
-
Jaké geometrické vztahy můžeme objevit na těchto obrázcích?
-
Krychlové stavby. Krychlová tělesa.
Sjednocení konečného počtu shodných krychlí tak, že každá má společnou stěnu s některou další krychlí. U krychlového tělesa (tvaru) nezáleží na orientaci v prostoru. Krychlová stavba je takovým sjednocením krychlí (opět tak, že každá má aspoň jednu stěnu celou společnou s další), které volně spočívá na rovné podložce.




nárys - půdorys - bokorys-
Úkol: Načrtněte nárys, půdorys a bokorys pro každou z níže zobrazených staveb z krychlí!



- Kótovaný půdorys.
-
Úkol: Kolik různých krychlových těles (tvarů) můžeme vytvořit ze čtyř krychlí?
Tvary ze čtyř krychlí (GeoGebra applet)Chiralita; https://en.wikipedia.org/wiki/Chirality / https://cs.wikipedia.org/wiki/Chiralita
Chemické enantiomery; https://en.wikipedia.org/wiki/Enantiomer / https://cs.wikipedia.org/wiki/Enantiomer
-
Tělesa (LN: Matematika pro páťáky) / názorné promítání
Rovnoběžné promítání / Středové promítání (Kapitola 16)
-
-
Metody práce v geometrii
Hošpesová, A. Metody práce v geometrii na 1. stupni ZŠ: Rýsování. Metodický portál RVP.CZ, 2014.
Literatura
- Fuchs, E., Zelendová, E. Metodické komentáře ke Standardům pro základní vzdělávání: Vzdělávací obor Matematika a její aplikace. NÚV, 2015. [PDF], [https://clanky.rvp.cz/clanek/c/Z/20617/METODICKE-KOMENTARE-K-OBORU-MATEMATIKA-A-JEJI-APLIKACE.html/].
- Hašek, R. Základy geometrie (KMA/ZGEOP) (studijní text), [ZGEOP_2018_Prednasky_3.pdf (vloženo 11. 12. 2018)].
- Hašek, R. Planimetrie (studijní text), [Planimetrie_studijni_text_2020.pdf (vloženo 19. 5. 2020)].
- Odvárko, O., Kadleček, J. Přehled matematiky pro ZŠ a víceletá gymnázia. Prometheus, Praha, 2004.
- Rámcový vzdělávací program pro základní vzdělávání. MŠMT, Praha, 2016, [http://www.nuv.cz/t/aktualne-platne-zneni-rvp-zv].
- Samková, L. Získávání předmatematických zkušeností v mateřské škole. South Bohemia Mathematical Letters, Volume 22 (2014), No. 1, 38-42. [http://home.pf.jcu.cz/~lsamkova/kipk/sbml.pdf]
- Standardy pro základní vzdělávání. [PDF],[http://www.nuv.cz/t/zarazeni-standardu-do-rvp-zv].
Další literatura pro hlubší studium
Kuřina, F. 10 geometrických transformací. Prometheus, Praha, 2002.
Kuřina, F. 10 pohledů na geometrii. Akademie věd České republiky, 1996.
Polák, J. Přehled středoškolské matematiky. Prometheus, Praha.
Pomykalová, E. Matematika pro gymnázia - Planimetrie. Prometheus, Praha, 2008.
Pomykalová, E. Matematika pro gymnázia - Stereometrie. Prometheus, Praha, 2014.
Jacobs, H. R. Geometry: seeing, doing, understanding. 3rd ed. New York: W.H. Freeman and Co., 2003.
Voráčová a kol., Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha, 2012.
Vyšín, J. a kol.: Geometrie pro pedagogické fakulty I. díl, SPN, Praha, 1965.
Eukleides, Eukleidovy základy (Elementa), překlad F. Servít, 1907.
Dostupné na https://commons.wikimedia.org/wiki/File:Eukleides_Servit.pdf
Internetové odkazy
Jednotné přijímací zkoušky - osmiletá gymnázia
Online kurzy
https://khanovaskola.cz ... Khanova škola
https://www.ixl.com ... IXL
Software ke stažení
www.geogebra.org ... program GeoGebra (možnost bezplatného stažení)
Materiály pro výuku a sebevzdělávání
Wolfram Demonstrations Project
www.cut-the-knot.org (Interactive Mathematics Miscellany and Puzzles)
http://www.math.uoc.gr (Geometrikon - galerie geometrických témat)
Roman Hašek, katedra matematiky PF JU, kontakt: hasek@pf.jcu.cz