Výpočetní technika pro matematiky I - KMA/VTM1

Předmět Výpočetní technika pro matematiky 1 poskytuje přehled možností využití počítače v matematice. Prostřednictvím řešení konkrétních problémů jsou podány základy užití počítačů, především programů GeoGebra a wxMaxima.

Obsah seminářů

1. Úvod do programu GeoGebra
   Nákresna, animace konstrukce, export na www.geogebra.org

   Příklad 1: Sestrojte trojúhelník ABC, je-li dáno: c=5 cm, v_c=6 cm, t_c=8 cm. Vytvořte animaci postupu a uložte ji na portál www.geogebra.org (sdíleno odkazem).

   Příklad 2: Výše uvedenou konstrukci modifikujte tak, aby bylo možno měnit velikosti daných prvků c, v_c, t_c trojúhelníku ABC.

   Úkol :  Vyberte si jednu konstrukční úlohu na trojúhelník z materiálu: Konstrukce trojúhelníku, tuto konstrukci sestrojte v programu GeoGebra, animujte a uložte na portál www.geogebra.org (sdíleno odkazem). Řešení úkolu doprovoďte stručným textem, v němž uvedete klíčové kroky konstrukce.

2. Graf funkce.
   Zobrazení grafu funkce v nákresně. Využití posuvníku při zkoumání vlastností grafu funkce.

   Příklad 1: Uvažujme exponenciální funkci f: y=a^x, kde základem a může být jakékoliv kladné reálné číslo s výjimkou 1. Existuje taková hodnota a, pro kterou je exponenciální funkce f rovna své derivaci? Odpověď hledejte prostřednictvím programu GeoGebra.

   Příklad 2: Sestrojte graf harmonické funkce f:y=asin(bx+c). Pomocí posuvníku vyšetřete vliv jednotlivých parametrů (a, b, c) na průběh grafu harmonické funkce.

   Úkol :  V tabulce uvedené zde si vyberte předpis funkce s parametrem, jejíž číslo je uvedeno u Vašeho jména v tomto seznamu. Funkci zobrazte v programu GeoGebra a pomocí posuvníku (posuvníků) vyšetřete vliv hodnot jednotlivých parametrů na průběh jejího grafu. Soubor exportujte na www.geogebra.org.

3. Tabulka programu GeoGebra.
   Propojení nákresny s tabulkou. Načítání dat do tabulky.

   Příklad 1:  Na obrázku je znázorněn list papíru, který je přehnut tak, že levý horní roh se dotýká spodního okraje v bodě P ve vzdálenosti x od levého dolního rohu. Představte si všechny možné takovéto polohy bodu P. Pro jaké x je obsah vyšrafovaného trojúhelníku na obrázku maximální?

   

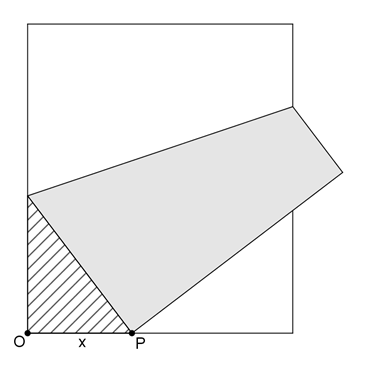
   Příklad 2:  Rádi bychom si z čtvercového kartonu o straně a vyrobili otevřenou krabičku na cukroví. Začneme tím, že si na karton načrtneme síť budoucí krabičky (viz obrázek), tj. v každém rohu kartonu vyznačíme čtverec o straně x, který představuje záložku při lepení krabičky. Najděte hodnotu x, pro kterou dostaneme krabičku o maximálním objemu.

   

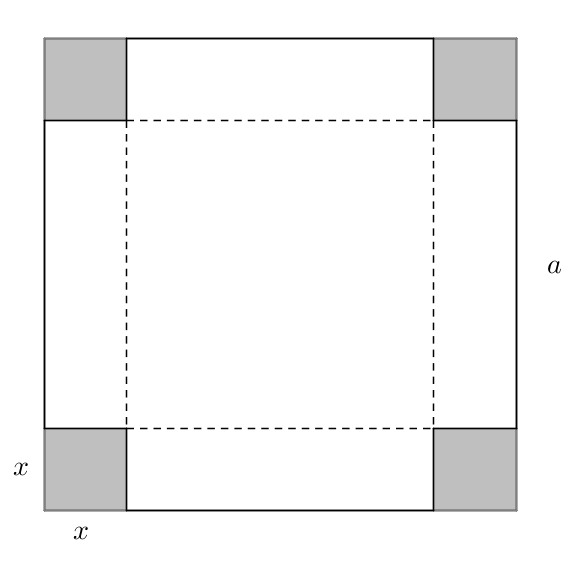
   Příklad 3:  Uvažujte obdélník o konstantním obvodu. Pro jaký poměr délek jeho stran a, b je jeho obsah maximální?.

   Úkol:  Najděte nebo vytvořte úlohu na výpočet extrému a tuto úlohu vyřešte v programu GeoGebra. Pokud je to možné a názornosti řešení prospěšné, využijte při tom Nákresnu, Tabulky i CAS. (Soubor exportujte na GeoGebraTube. O řešení úkolu vypracujte záznam do svého dokumentu ve společném adresáři na Google Disku.) [Hotové úlohy nebo náměty na vytvoření úloh nových můžete čerpat zde: 1, 2, 3 (Převzato z WEIMER, R. C.Applied Calculus with Technology. Brooks/Cole Publishing Company, 1998.)]

4. Feynmanův trojúhelník (One-seventh area triangle).
   

   Příklad:   Uvažujme libovolný trojúhelník ABC (viz obrázek). Vždy v jedné třetině každé jeho strany umístíme postupně body P, Q, R a spojíme je s protilehlými vrcholy. Průsečíky těchto spojnic jsou vrcholy trojúhelníku KLM. Ověřte a dokažte (synteticky nebo analyticky; případně najděte důkaz na internetu a interpretujte ho v GeoGebře) tvrzení, že obsah trojúhelníku KLM je jednou sedminou obsahu trojúhelníku ABC.

   

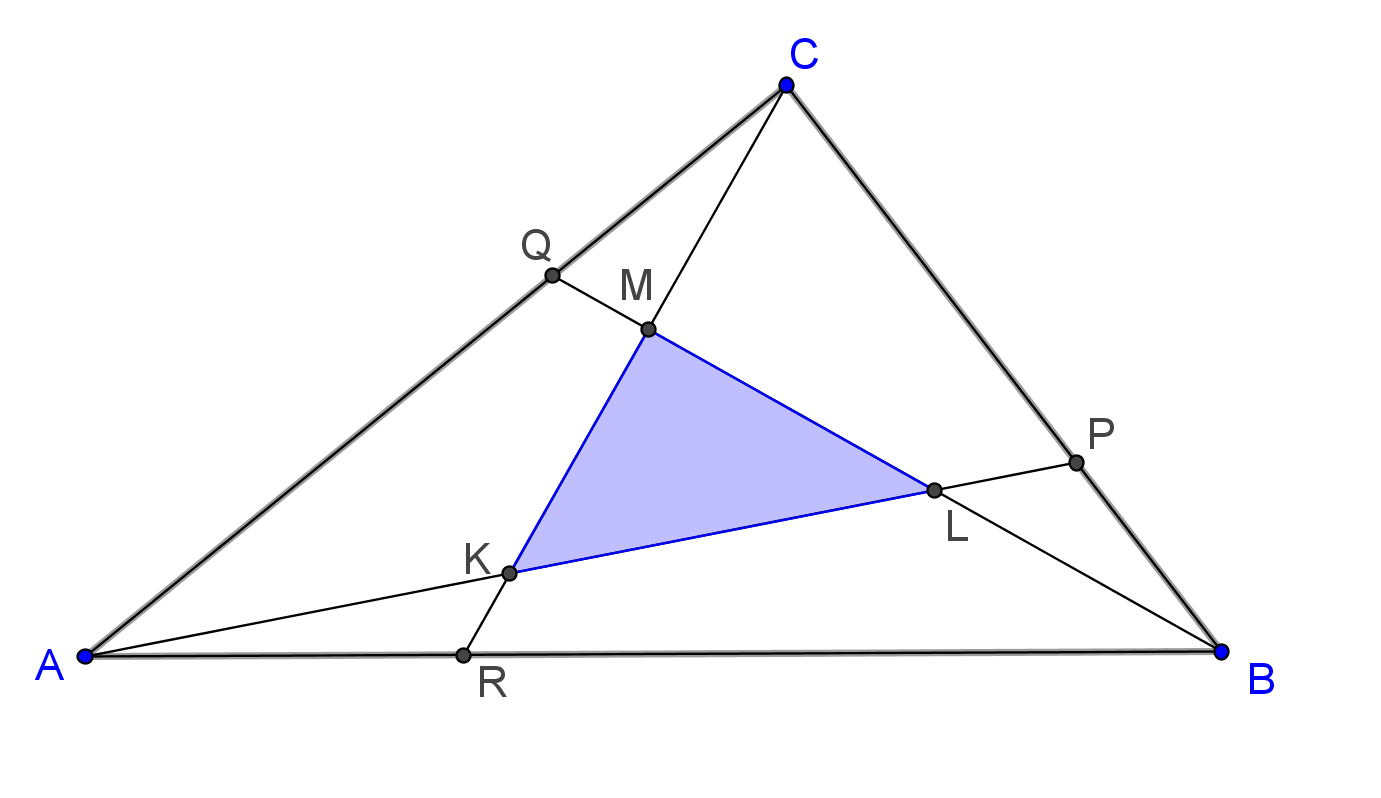
5. Tvorba GeoGebraBooku.
   Společně vytvořený cvičný GeoGebraBook: Kuželosečky.
6. Rovnice a nerovnice.
   Řešení algebraických rovnic a jejich soustav, goniometrických rovnic, transcendentních rovnic a vybraných nerovnic užitím programu wxMaxima a GeoGebra.

   Úkol:  Užitím programů wxMaxima a GeoGebra řešte úlohy zadané v dokumentu ReseniRovnic.pdf.
   Možné postupy řešení uvedených úloh ve wxMaximě: algebraické rovnice, soustavy algebraických rovnic, goniometrické rovnice, numerické řešení rovnic, nerovnice.

7. Množiny bodů dané vlastnosti
   Kombinace geometrických a algebraických nástrojů

   Příklad 1:  V rovině jsou dány dva různé body A, B (volte např. A=[-5,0], B=[5,0]). Určete množinu (její podobu a analytické vyjádření) všech bodů X z dané roviny, pro které platí |AX|/|BX|=k, kde |AX|, |BX| jsou vzdálenosti bodu X od bodu A, resp. B a k je reálná konstanta (volte např. k=2).

   Příklad 2:  Uvažujte body A, B z předchozího příkladu a pokuste se určit množiny všech bodů X v rovině, které vyhovují následujícím podmínkám pro vzdálenosti |AX| a |BX|:
   a) |AX|·|BX|=k,
   b) |AX|+|BX|=k,
   kde k je opět reálná konstanta.

   Příklad 3:  Jednoduchý žebřík délky l stojí opřený o zeď. Na jednom stupni žebříku, ve vzdálenosti a od jeho paty, spí kočka. Po jaké trajektorii se pohybuje (tvrdě) spící kočka, jestliže se žebřík začne klouzáním po podlaze, tedy i po zdi, pohybovat směrem k zemi. Uvažujte různé hodnoty a.

   Úkol:  Pro závěrečný úkol si můžete vybrat jednu z následujících možností:

   • Vytvoření "matematického obrázku" (v duchu toho, který jsme vytvářeli na seminářích 19. 11.) s těmito vlastnostmi: 1) použití alespoň 4 matematických funkcí, 2) definování obrazců pomocí nerovnic a jejich soustav, 3) přítomnost alespoň 2 animovaných objektů, z toho jedna fotografie.
   • Určení (obrázek i rovnice) množiny bodů daných vlastností pomocí programu GeoGebra nebo wxMaxima. Zadání najdete zde: "F. Kuřina, 10 pohledů na geometrii, str. 139". Přitom můžete řešit jenom takovou úlohu z uvedeného seznamu, u jejíhož čísla se poslední číslice shoduje s poslední číslicí Vašeho osobního čísla, nebo je o jednu menší (v případě 0 se jedná o číslici 9), nebo o jednu větší (v případě 9 uvažujte 0).

8. Program wxMaxima ve výuce matematiky.
   Užití programu wxMaxima pro základní výpočty a zobrazení grafů.

   Úkol:  Prostudujte článek "Program wxMaxima ve výuce matematiky" a samostatně vyřešte všechny uvedené příklady. Každému příkladu věnujte zvláštní soubor, jehož součástí bude kromě výpočtu i zadání úlohy. Soubory uložte do složky s Vaším jménem na Google Disku.

Literatura pro samostudium (online)

1. Günzel, M. a kol.: Integrace elektronických prostředí pro počítačem podporovanou výuku matematiky. Jihočeská univerzita v Č. B., 2012. Dostupné z http://home.pf.jcu.cz/~ippvm/archives/category/publikace
   
2. Hohenwarter, M., Hohenwarter, J. Introduction to GeoGebra, Version 4.2 Dostupné z http://www.geogebra.org/book/intro-en.pdf
   

Další doporučená literatura

• J. Böhm et al.: The Case for CAS
• R. Hašek: Užití Derive ve výuce matematiky (pdf) [online]
• Hašek, R., Petrášková, V. GeoGebra in financial education. North American GeoGebra Journal, Vol. 2, No. 1, 2013, Miami University, USA, ISSN: 2162-3856, pp. 31-36. Dostupné z http://www.ggbmidwest.com
  
• Hašek, R. Numerical analysis of a planar motion; GeoGebra as a tool of investigation. North American GeoGebra Journal (ISSN: 2162-3856). Miami University, Oxford, OH, USA. Vol. 1, No. 1, 2012. pp. 33 - 36. Dostupné z http://www.ggbmidwest.com
  
• J. Leydold, M. Petry: Introduction to Maxima for Economics (pdf) [online]

Internetové odkazy

GeoGebra
www.geogebra.org ... stránka věnovaná volně šiřitelnému programu GeoGebra, možnost stáhnutí instalace a manuálů, příklady použití, další odkazy
www.youtube.com/user/GeoGebraChannel ... GeoGebra na YouTube
www.geogebra.org/materials/ ... Volně dostupné materiály vytvořené v GeoGebře
GeoGebra Kniha ... Návod na tvorbu online "knihy".
GeoGebra Skupina ... Návod na práci se "skupinou".

Dynamická geometrie
i2geo.net ... I2G Intergeo - mezinárodní portál pro sdílení materiálů dynamické geometrie

Maple
www.maplesoft.com ... oficiální stránka Maple
www.maplesoft.cz ... prodejce Maple v ČR
Přehled základních příkazů Maple   Základy práce s programem Maple (pdf)  

Derive
www.austromath.at/dug ... Derive Users Group
education.ti.com ... Texas Instruments
home.pf.jcu.cz/~hasek/Derive6.html ... učební materiály pro úvod do práce s programem Derive, řešené úlohy, archivní materiály k výuce programu Derive od roku 2005

wxMaxima / Maxima
wxmaxima.sourceforge.net ... stránka věnovaná volně šiřitelnému CAS programu wxMaxima, možnost stáhnutí instalace, příklady použití, další odkazy, například na fórum uživatelů
maxima.sourceforge.net ... Maxima

Sage
www.sagemath.org
www.sagenb.org

LaTeX
Drsný úvod do Latexu
Ne příliš stručný úvod do systému LATEX
LaTeX (Wikibooks)

Matematika kolem nás
Maths in the City
Plus magazine ... living mathematics

Požadavky na studenta

• Vytvoření originální GeoGebra Knihy