GEOMETRIE III - KMA/7G3

Geometrie III - text (fáze 1)

GeoGebra: [Rovnoběžné promítání] [Středové promítání]

Úkol:  V programu GeoGebra zobrazte kulovou plochu. Použijte různé druhy promítání. Porovnejte výsledky pravoúhlého a kosoúhlého promítání.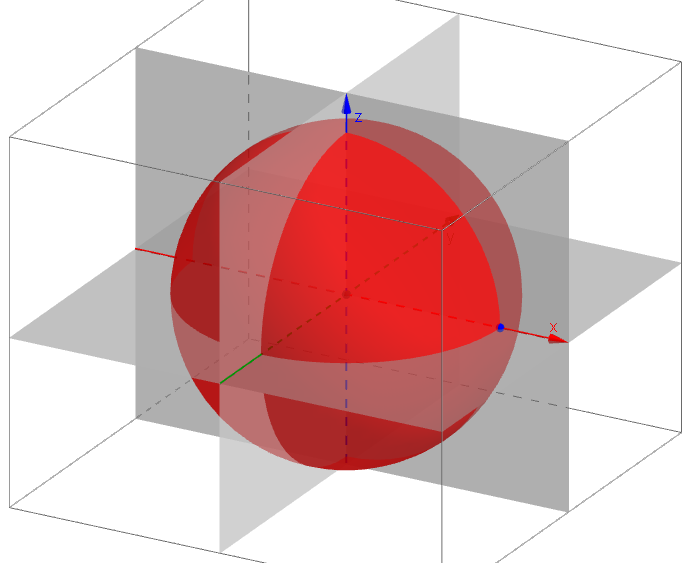

Kulová plocha v kosoúhlém promítání

Testy prostorových schopností (orientace v prostoru, tvorba prostorových představ a manipulace s nimi)

• Santa Barbara Solids Test (https://www.silc.northwestern.edu/santa-barbara-solids-test-inferring-cross-sections-of-3d-objects-2/)
• Purdue Visualization of Rotations Test (https://usu.instructure.com/courses/387855/quizzes/528051)
• Spatial Reasoning Test (https://www.assessment-training.com/spatial-reasoning)

Optické iluze

• https://interestingengineering.com/this-cube-is-not-moving-optical-illusions-that-bend-your-brain?
• https://www.idnes.cz/technet/veda/opticke-iluze-illusion-of-the-year-video.A160712_132525_veda_pka
• https://www.idnes.cz/technet/veda/opticka-iluze-kognitivni-zkresleni-shepardovy-stoly-shepards-tables.A170426_134159_veda_pka

Geometrie III - text (fáze 2)

Úkol:  Nakreslete, sestavte ze stavebnice či najděte na internetu všemožná geometrická tělesa. Pokuste se je pojmenovat a popsat jejich vybrané geometrické vlastnosti. Inspirujte se na stránce https://en.wikipedia.org/wiki/Solid_geometry.

Geometrie III - text (fáze 3)

Úkol:  Každé z těles uvedených na str. 10-11 textu Geometrie III - text (fáze 3) zobrazte v programu GeoGebra. Alespoň pro vybraná z nich potom využijte možnost programu měnit metodu promítání (axonometrie, perspektiva, kosoúhlé promítání) a směr pohledu na zobrazovaný objekt (půdorys, nárys a bokorys) a všemi těmito způsoby si je zobrazte. Pokuste se popsat některé zjevné odlišnosti v zobrazení téhož tělesa různými metodami.

Geometrie III - text (fáze 3)

Úkol:  U geometrických zobrazení nás zajímají vlastnosti a charakteristiky, které se při nich zachovávají, tj. platí jak pro vzor, tak i pro jeho obraz, říkáme jim invarianty<\i> daného zobrazení. Známe například tvrzení, že se při určitém zobrazení “zachovává incidence”. Zjistěte experimentálně, zda se u rovnoběžného a středového promítání zachovává střed úsečky. Své závěry se pokuste dokázat.

Geometrie III - text (fáze 4)

Geometrie III - text (fáze 5)

Úkol:  Zobrazte kvádr o rozměrech 3, 4 a 5 cm prostřednictvím těchto zobrazovacích metod:
a) Volné rovnoběžné promítání.
b) Kosoúhlé promítání (ω = 150°, 3/4).
c) Kavalírní perspektiva (ω = 135°).
d) Vojenská perspektiva (ω = 135°).
(Dle vlastního uvážení zvolte pravotočivou nebo levotočivou soustavu souřadnic. Rýsujte nebo kreslete od ruky.)

Geometrie III - text (fáze 6)

Úkol 1:  Určete délku úsečky AB; A[-4;2;5], B[2;-2;1].
[3D znázornění (GeoGebra), Animace řešení, varianta 1, Animace řešení, varianta 2]

Úkol 2: V kótovaném promítání jsou dány průměty bodů A, B; |A₁B₁| = 7 cm, zA=5, zB=2. Určete: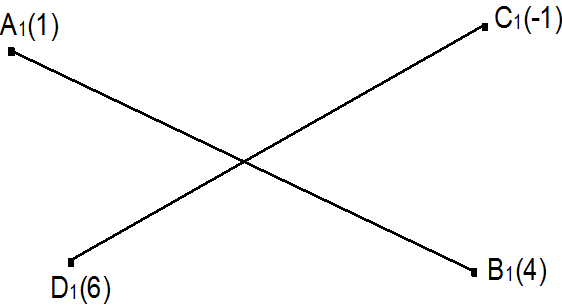
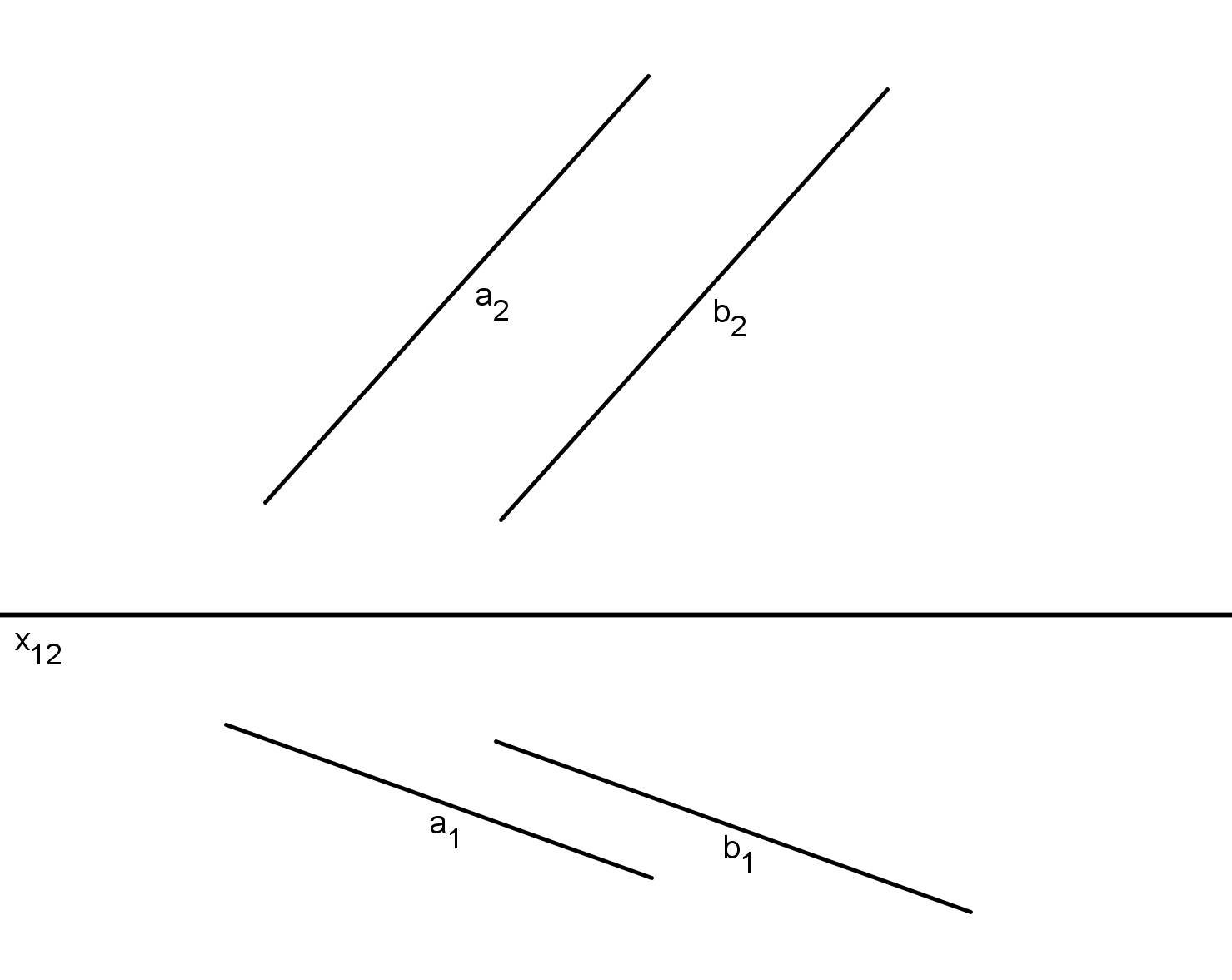
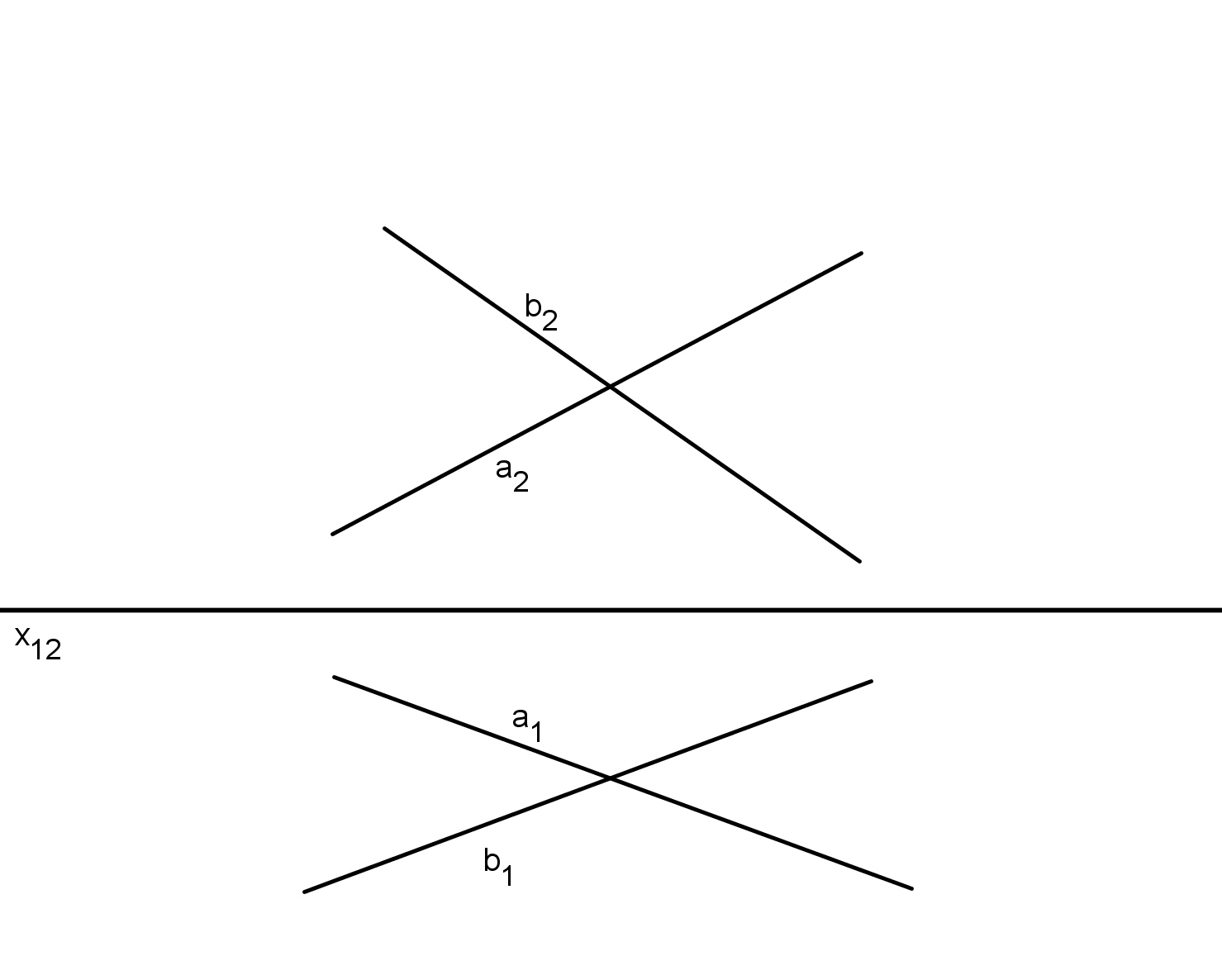
a) Stopník přímky AB.
b) Odchylku α přímky AB od průmětny.
c) Skutečnou velikost úsečky AB.
d) Vystupňujte přímku AB.
[Zadání v PDF]

Geometrie III - text (fáze 7)

Úvod do Mongeova promítání - zobrazení bodu, přímky a roviny.

Úkol 1: Sestrojte stopy roviny dané (i) třemi body, (ii) dvěma rovnoběžkami. [Zadání v pdf]

Úkol 2: Sestrojte sdružené průměty hlavních přímek h, f roviny σ, která je dána dvěma rovnoběžkami a, b. Zobrazte stopy roviny σ. [Animace]

Řešené příklady z přednášky:

Příklad 8: Sestrojte stopy roviny σ dané různoběžkami a, b.  [Animace (stopníky)] [Animace (hlavní přmky)]

Příklad 9: Sestrojte stopy roviny σ dané bodem A a přímkou b.   [Animace]

Úkol:  Sestrojte stopy roviny dané přímkami a, b (Zadání v PDF) :

Rovina je určena dvěma rovnoběžkami

Rovina je určena dvěma různoběžkami

Geometrie III - text (fáze 8)

Mongeovo promítání II (metrické úlohy, kružnice).

Příklad 1: Určete skutečnou velikost úsečky AB; A = [3; -1; 2], B = [0; 3; 3,5].   [Animace]

Příklad 2: Určete sdružené průměty přímky AB, která leží v rovině ρ(-5; 5; 4); A = [0; 2; ?], B = [2; 1; ?].
[Animace, 3D znázornění: Přímka v rovině (GeoGebra 3D)]

Příklad 3: Určete průsečík přímky AB s rovinou ν(-4; 4; 5), A = [2; 1; 0], B = [-5; 4; 8].   [Animace]

Příklad 4: Bodem K = [2; 3; 4] veďte přímku kolmou k rovině ρ(-3; 4; 4).

Příklad 5: Určete vzdálenost bodu V=[5; 7; 7] od roviny ρ = (5; 4; 6). [Animace - sklopením]   [Animace - otočením]

Příklad 6: Sestrojte v Mongeově promítání sdružené průměty kružnice k, která leží v rovině kolmé na nákresnu. [Animace]

Příklad 7: Sestrojte v Mongeově promítání sdružené průměty kružnice k, která leží v obecně umístěné rovině. [Animace]

Geometrie III - text (fáze 9)

Mnohostěny.

Krychle – kvádr – hranol  /  Hranolová plocha – hranol

Objem jehlanu (You Tube)

Úkol: Ze stavebnice vytvořte různé mnohostěny. U každého určete počet jeho vrcholů, stěn a hran a tyto údaje zaznamenejte do tabulky. Hledejte výraz obsahující tyto údaje, jehož hodnota je pro všechny mnohostěny, případně jejich většinu, stejná.

Euler's Formula (www stránka)  /  Wikipedia: Euler characteristic  /  dynamický (topologický) důkaz

Pravidelné mnohostěny (Platónská tělesa)

Pravidelné mnohostěny.

Platónská tělesa: Wikipedia: Platonic solid.

Dualita Platónských těles: [4-4 | 6-8 | 12-20]

Geometrie III - text (fáze 9)

Úkol:  V programu GeoGebra, konkrétně v Grafickém náhledu 3D, proveďte řez čtyřbokého jehlanu ABCDE rovinou FGH. Sestrojte tak, aby bylo možné měnit parametry jehlanu i roviny tažením myší. (Inspirace viz https://www.geogebra.org/m/mpe4dbfn)

Úvod do středové kolineace a osové afinity / Středová kolineace (převzato z textu R. Hašek: Geometrie 4) / Osová afinita (převzato z textu R. Hašek: Geometrie 3)

GeoGebra: [Středové promítání] [Středová kolineace] [Rovnoběžné promítání] [Osová afinita]

Úkol 1:  V programu GeoGebra 5 vytvořte modely těles dle níže uvedených obrázků i s popisem zobrazených bodů. Potom sestrojte řezy těchto těles rovinami určenými body A'B'C', resp. A'B'D'.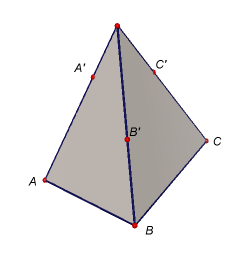

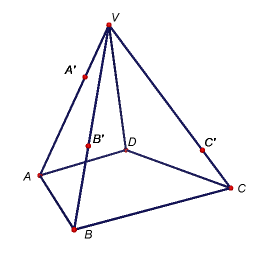
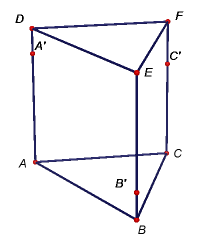
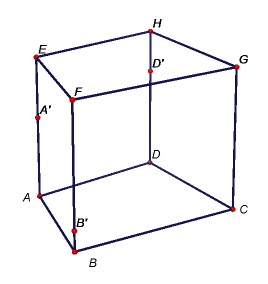
Úkol 2:  Osová afinita v rovině je dána osou o a dvojicí bodů P, P'. Sestrojte obraz daného trojúhelníku ABC. [Zadání v GeoGebře]

Příklad: Je dána přímka o a trojúhelník ABC. Sestrojte obraz A'B'C' trojúhelníku ABC v takové osové afinitě, aby byl trojúhelník A'B'C' rovnostranný. [Řešení v GeoGebře]

Úkol 3:  Sestrojte řez kvádru ABCDA'B'C'D' rovinou MNP; M je vnitřní bod hrany CC', pro který platí 4|CM|=|CC'|, N je střed hrany A'D' a bod P leží na prodloužení hrany B'B za bod B a platí 3|BP|=|BB'|.
(J. Polák: Přehled středoškolské matematiky, str. 481, Zadání v GeoGebře)

Geometrie III - text (fáze 9)

Aplikace osové afinity: Elipsa jako afinní útvar ke kružnici.

Příklad: Ve volném rovnoběžném promítání zobrazte krychli, která má na stěnách nakresleny kružnice o průměru a (délka hrany krychle). [Krychle s kružnicemi na stěnách.] [Řešení v programu GeoGebra.]