Matematika I - KMA/8M1

Předmět Matematika I je věnován detailnímu seznámení se základy elementární geometrie v rovině a v prostoru. Pozornost je věnována především shodným a podobným zobrazením, vzájemným polohám geometrických útvarů, způsobům jejich zobrazování a postupům určování jejich rozměrů, vzdáleností a odchylek.

Kompletní učební text ve formátu PDF: Hašek: Úvod do geometrie (poslední aktualizace 3. 10. 2019).

Osnova předmětu

• Úvod do geometrie.

  Přednáška:	Úvod do geometrie Jakou geometrickou vlastnost znázorňují následující obrázky?
  Cvičení:	Vizuální důkaz Pythagorovy věty (odpovídá důkazu představenému v textu na str. 4, Obr. 1) Perigalův důkaz Pythagorovy věty / Henry Perigal (1801-1898) Zadání úloh pro cvičení. Domácí úkol: Vytvořte pomůcku pro provedení vizuálního důkazu Pythagorovy věty, představeného v textu na str. 4 na Obr. 1.

• Geometrické útvary v rovině.

  Přednáška:	Úvod do geometrie: str. 9-15, 18-26 Online tangram
  Cvičení:	Zadání úloh pro cvičení. Spiral of Theodorus (Wikipedia)

• Mnohoúhelníky.

  Přednáška:

  Úvod do geometrie: str. 18-35

  Cvičení:

  ÚKOL: Kolik různých trojúhelníků (všechny vzájemně shodné uvažujeme jako jeden) můžeme vytvořit na geoboardu 3x3? Umíte je všechny pojmenovat (tj. použít pojmy pravoúhlý, rovnoramenný, tupoúhlý, ...)? Umíte u všech určit obsah (pokud předpokládáme, že vzdálenost sousedních kolíků desky je 1)? Zkuste to! Trojúhelníky nakreslete a opatřete výpočty obsahů. Můžete použít tento online Geoboard. Více o této důležité pomůcce viz např. https://en.wikipedia.org/wiki/Geoboard.

  Přednáška:	Kapitola 4 ÚKOL: Co mají uvedené dva obrázky (a tojúhelníky na nich zobrazení) společné a čím se liší?
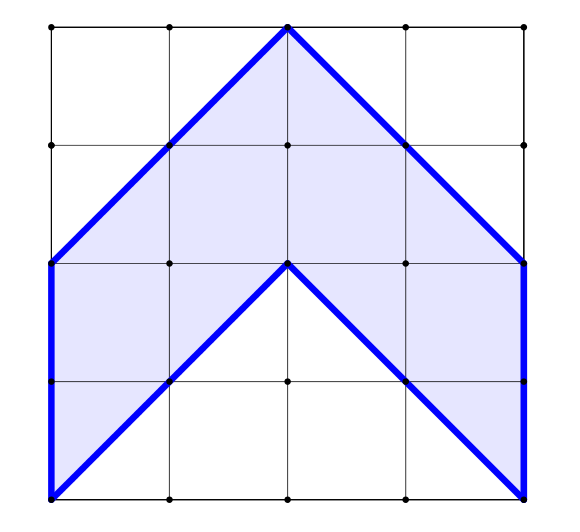
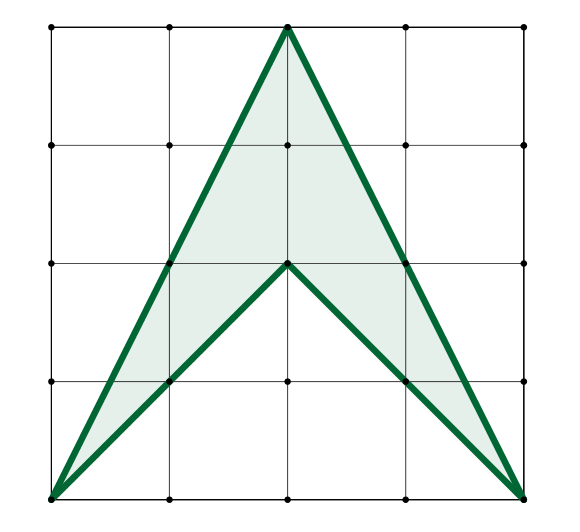
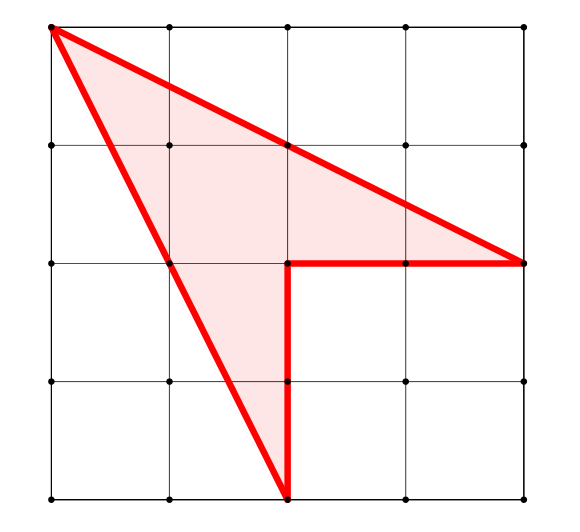
  Cvičení:	ÚKOL: Vypočítejte obsahy uvedených obrazců. Zadání úloh pro cvičení (Cvičení 4).   [Řešení cvičení 4] Literatura pro další studium: Jordánová, D. Obsah a obvod obrazce s využitím čtvercové sítě ve výuce geometrie na 1. stupni ZŠ. Závěrečná práce DVPP - Učitelství pro 1. stupeň ZŠ. České Budějovice: Jihočeská univerzita v Č. B. 2020.

• Délka úsečky. Dimenze prostoru. Obsah. Využití čtvercové sítě. Měření úhlu.

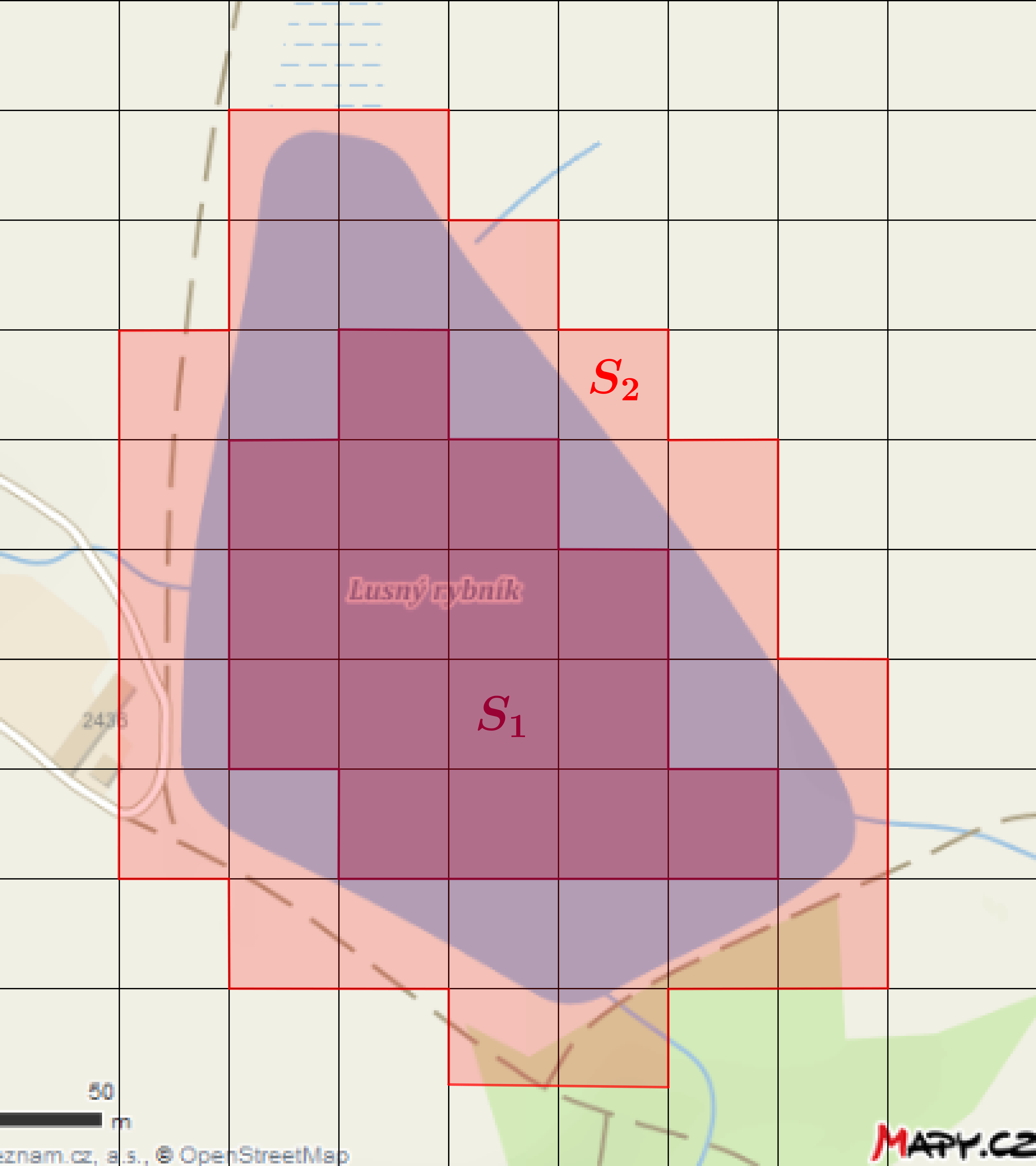
  Přednáška:	Kapitoly 6 (dimenze), 7 (míra), 5 (mnohostěny) a 4 (mnohoúhelníky) Rybník Lusný (Mapy.cz) [Lusný - čtvercová síť] Odvození vztahu pro výpočet obsahu kruhu - grafický důkaz (video)
  Cvičení:	Zadání úloh pro cvičení (Cvičení 5).   [Řešení cvičení 5]

• Pravidelné mnohoúhelníky. Pokrytí roviny. Symetrie.

  Přednáška:	Kapitoly 4.8 (pravidelné mnohoúhelníky), 5 (mnohostěny)
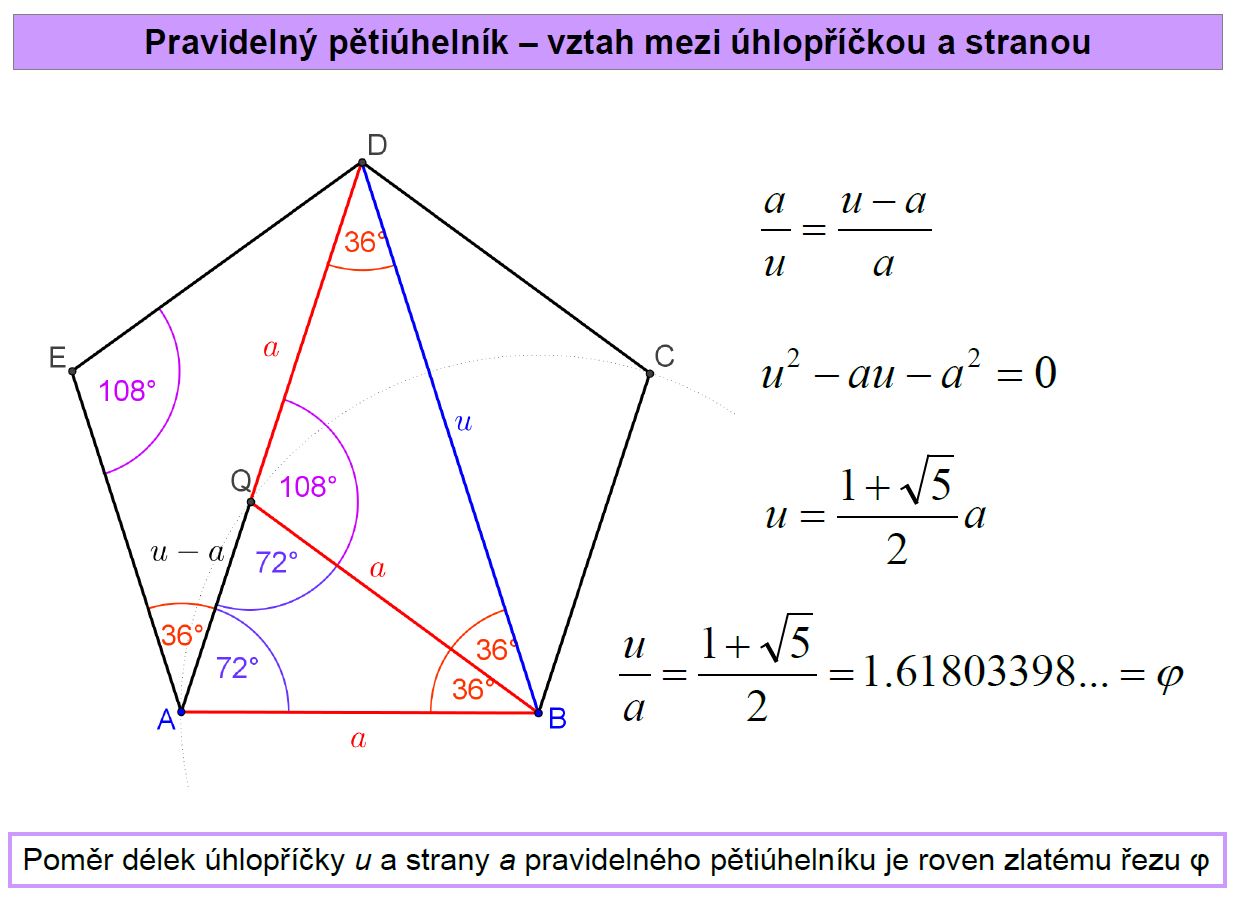
  Cvičení:	Zadání úloh pro cvičení (Cvičení 6).   [Řešení cvičení 6]

• Geometrické útvary v trojrozměrném prostoru.

  Přednáška:

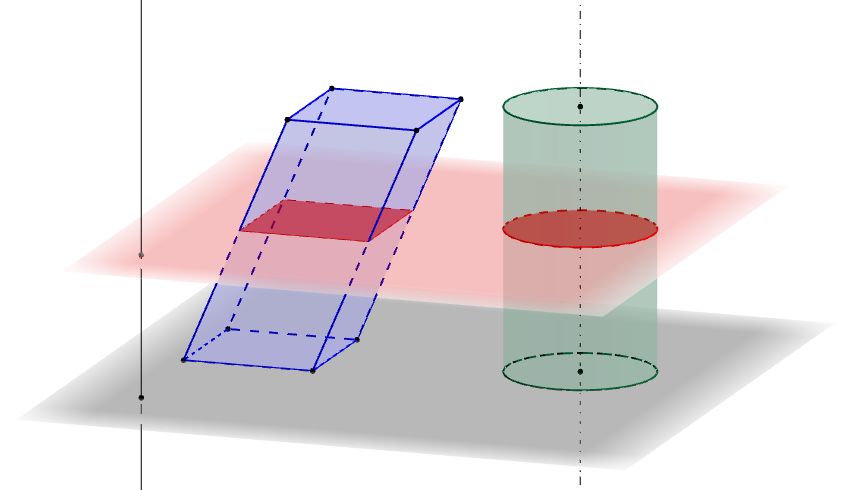
  Kapitoly 5, 11, 16 Krychle prince Ruprechta The trouble with five Pravidelné mnohostěny. Eulerův vztah. (prezentace) / Euler's Formula (www stránka) Cavalieriho princip / Cavalieri's principle (Wikipedia)

  Cvičení:

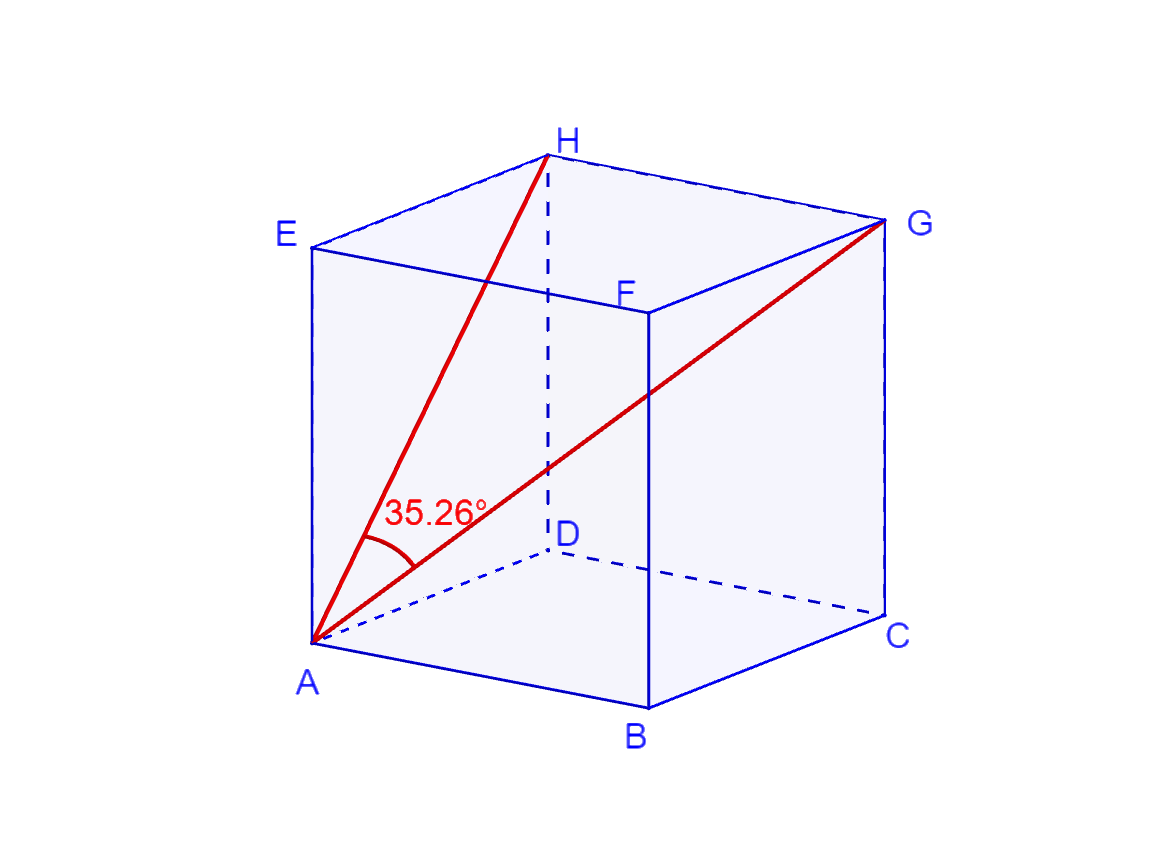
  Jak vypočítáme odchylku mezi stěnovou a tělesovou úhlopříčkou v krychli? [GeoGebra applet] Zadání úkolu pro cvičení: Na stránce Paper Models of Polyhedra si vyberte mnohostěn, vytiskněte si jeho síť a slepte model. Pokud se rozhodnete pro mnohostěn, který má méně než 10 stěn, vyberte si k němu ještě alespoň jeden další, tak, aby součet počtů jejich stěn byl alespoň 10. Výsledek nafoťte a vložte do MS Teams, kde bude tento úkol rovněž zadán.

• Stereometrie. Zobrazení trojrozměrného útvaru. Volné rovnoběžné promítání.
• Sdružené průměty trojrozměrného útvaru. Stavby z krychlí. Kótované promítání.

  Přednáška:	Rovnoběžné promítání. Středové promítání Kapitola 16 LN: Matematika pro páťáky Stavba z krychlí (str. 94) nárys - půdorys - bokorys Úkol:  Načrtněte nárys, půdorys a bokorys pro každou z níže zobrazených staveb z krychlí! Matika.in: Stavby z kostek Úkol:  Kolik různých krychlových těles (tvarů) můžeme vytvořit ze čtyř krychlí? Řešení: Tvary ze čtyř krychlí (GeoGebra applet)
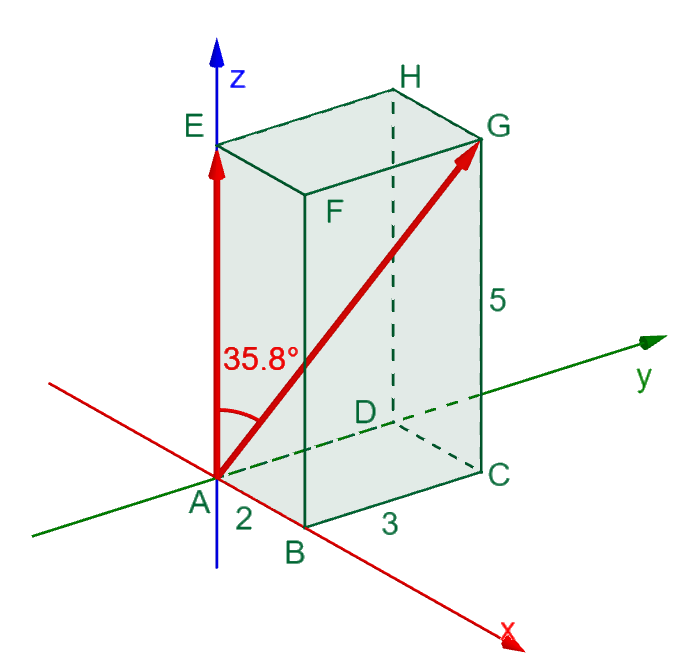
  Cvičení:	Skalární součin Kapitola 7.4 (str. 48) Zadání úkolu pro cvičení: Vypočítejte odchylku hrany a tělesové úhlopříčky kvádru o rozměrech 2 x 3 x 5, viz obrázek. [GeoGebra applet]

• Planimetrie. Symetrie roviny. Geometrická zobrazení. Shodnost v rovině.

  Přednáška:

  Kapitola 12         Symmetry in Nature Symmetry in Geometry (Video) Geometrická zobrazení (v rovině) GeoGebra - Nákresna Kapitola 13 Shodná zobrazení

  Cvičení:

  Wikipedia: Symmetry [Osová souměrnost]   [Otočení]   [Středová souměrnost]   [Posunutí]   [Posunutá souměrnost] Úkol: Je dána přímka p a body A, B v téže polorovině s hraniční přímkou p. Najdete všechny body X ∈ p takové, že součet vzdáleností |AX| + |BX| je minimální. (Tato úloha je známa jako Heronův problém; Hérón Alexandrijský, přibl. 10-70 n.l.) Zadání úloh pro cvičení (Cvičení 9).   [Řešení cvičení 9] [Příklad 8 (Rotace rovnostranného trojúhelníku)]   [Příklad 9 (Zobrazení reprodukující rovnostranný trojúhelník)]   [Příklad 10 (Obdélník a jeho obraz v otočení)] Zadání úloh pro cvičení (Cvičení 10). Řešení cvičení 10 (GeoGebra applety): [Příklad 1] [Příklad 2] [Příklad 3] [Příklad 4] [Příklad 5] [Příklad 6]

• Osová souměrnost. Osově souměrné útvary. Středová souměrnost. Středově souměrné útvary.
• Posunutí. Otočení. Posunuté zrcadlení.

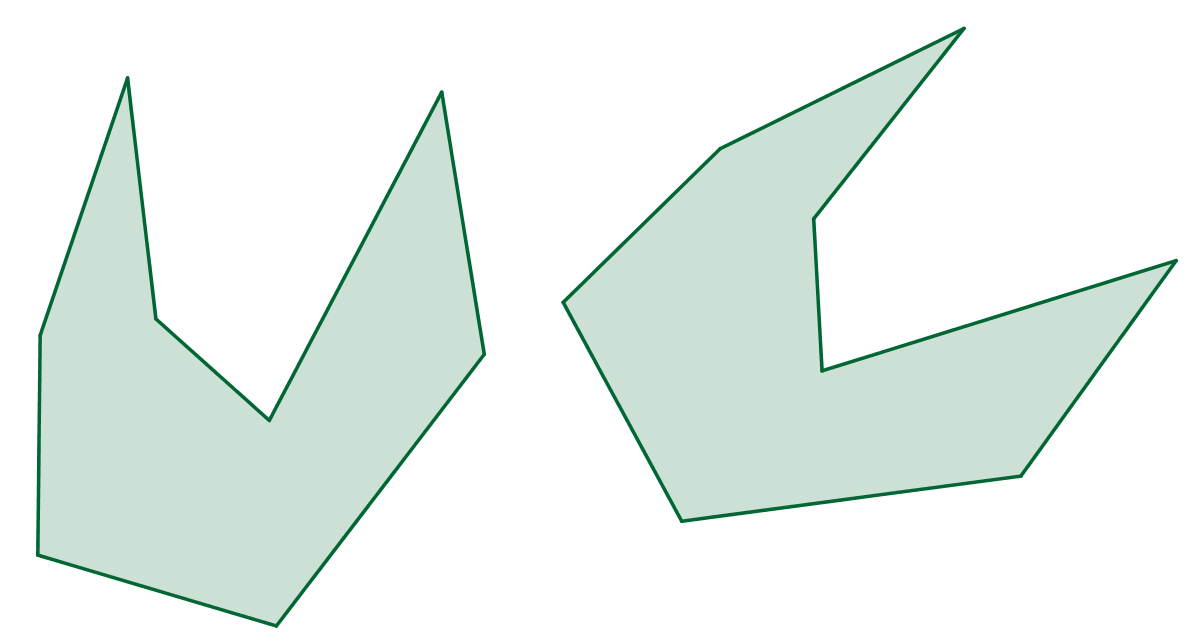
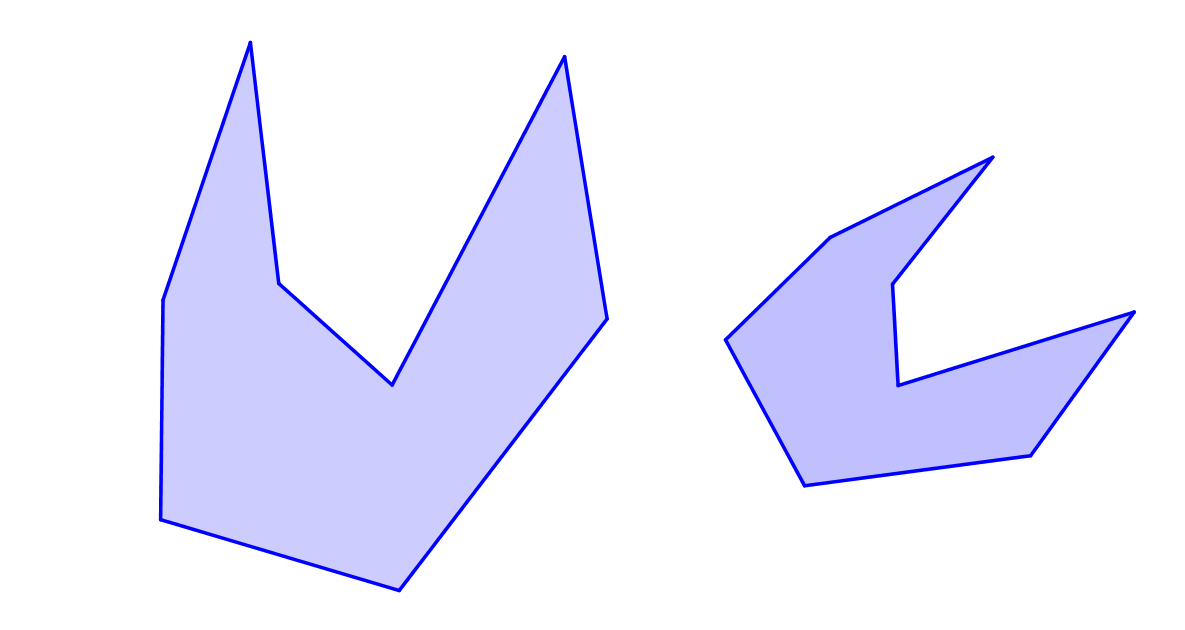
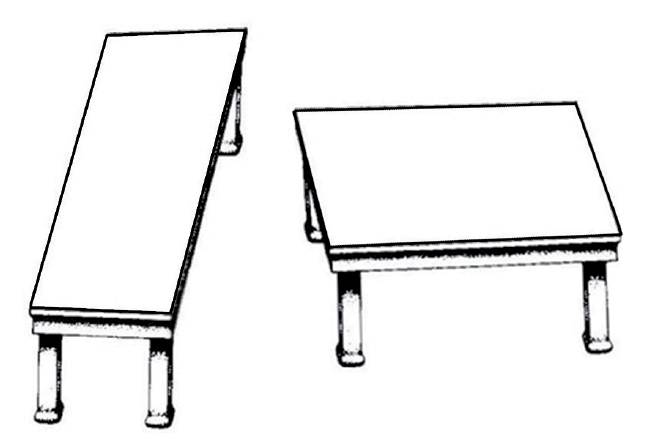
  Přednáška:	Kapitola 13 Které z dvojic útvarů jsou vzájemně shodné či podobné?   Shepard's tables   GeoGebra - Nákresna
  Cvičení:	Zadání úloh pro cvičení (Cvičení 10). Řešení cvičení 10 (GeoGebra applety): [Příklad 1] [Příklad 2] [Příklad 3] [Příklad 4] [Příklad 5] [Příklad 6] Domácí úkol na výpočty obsahů ve čtvercové síti: Zadání (14. 12. 2022).

• Skládání geometrických zobrazení.

  Přednáška:	Kapitola 13 Složení dvou osových souměrností, jejichž osy jsou na sebe kolmé. 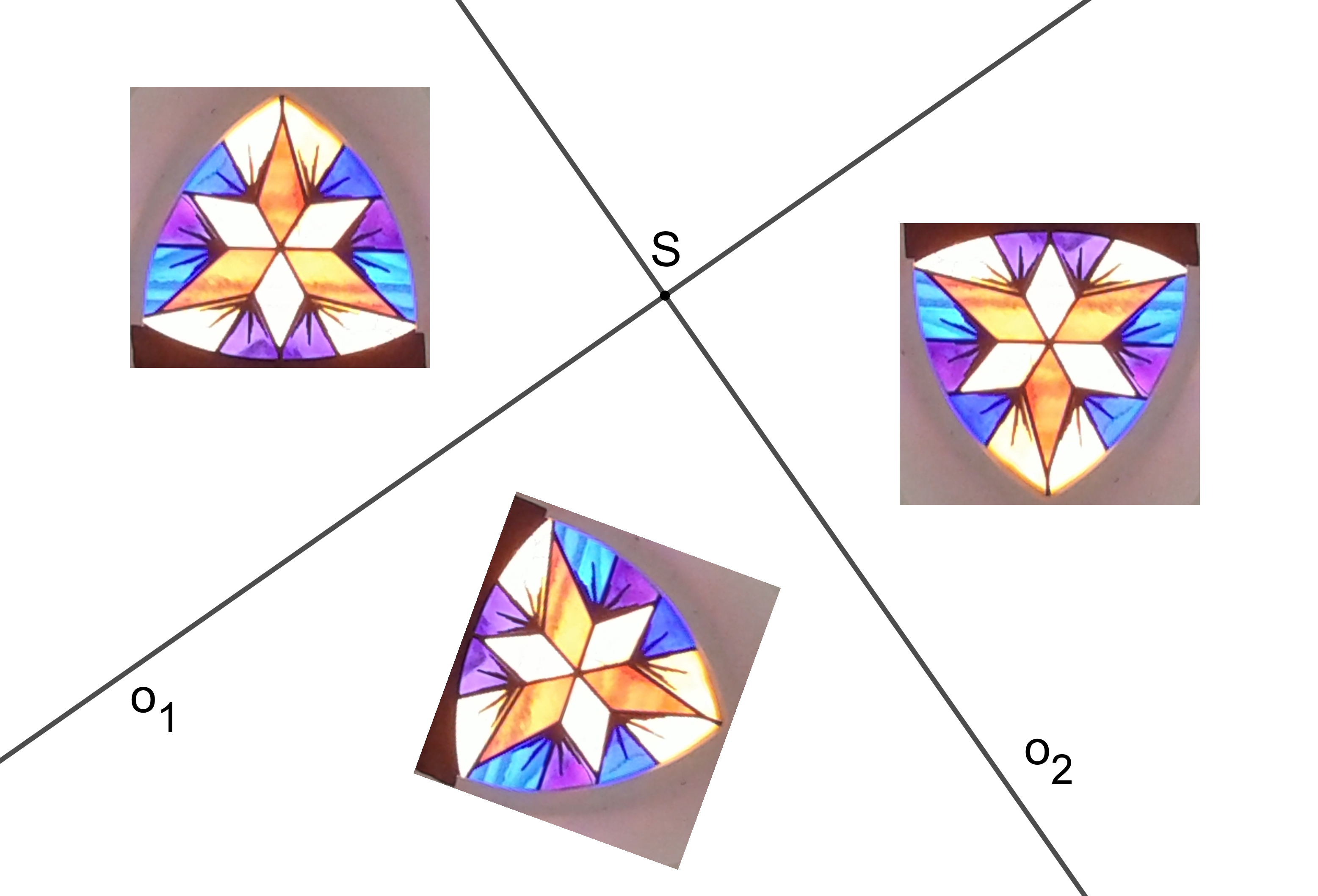[GeoGebra applet]
  Cvičení:

• Podobnost. Podobné zobrazení v rovině a v prostoru.

  Přednáška:

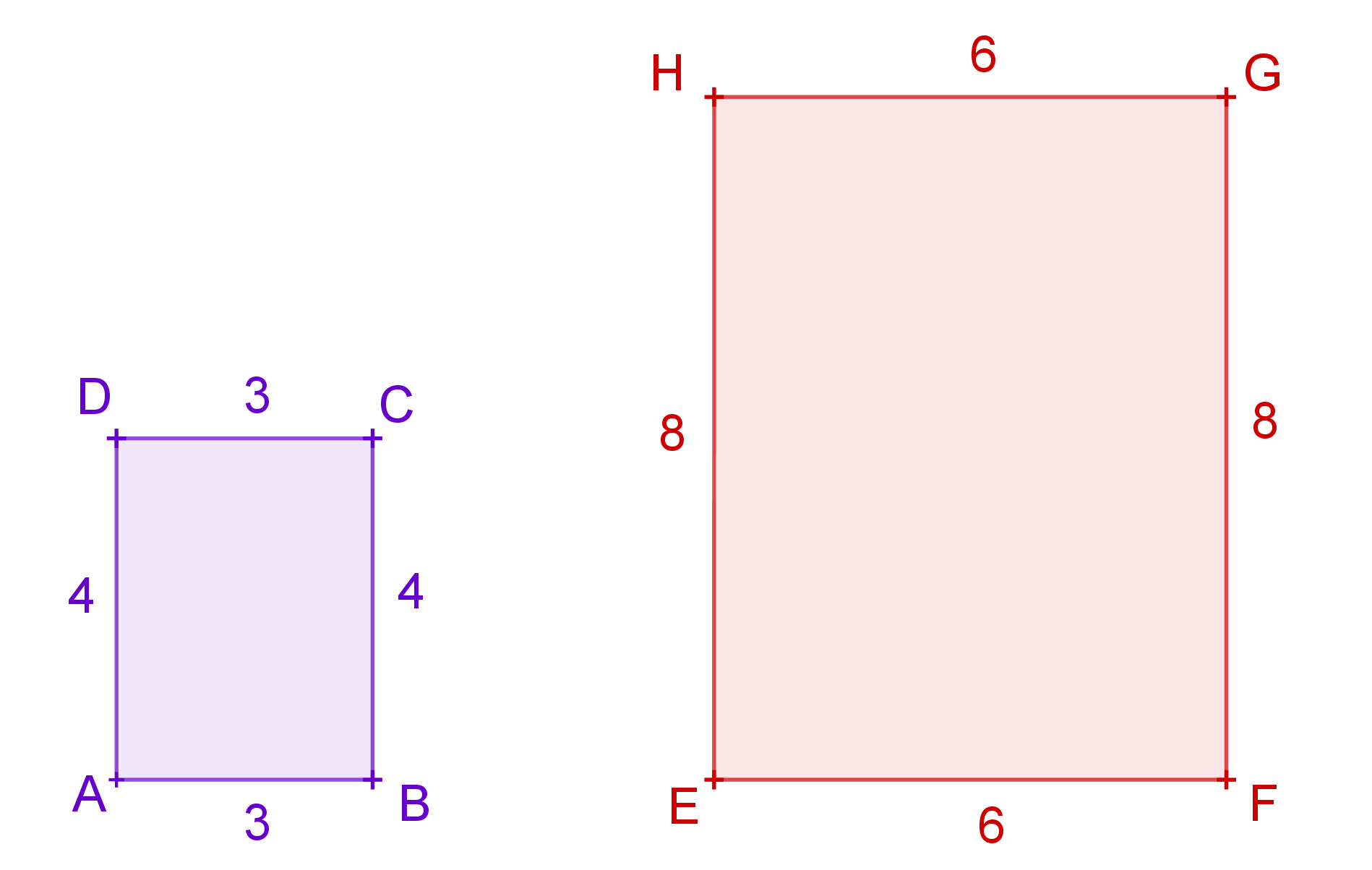
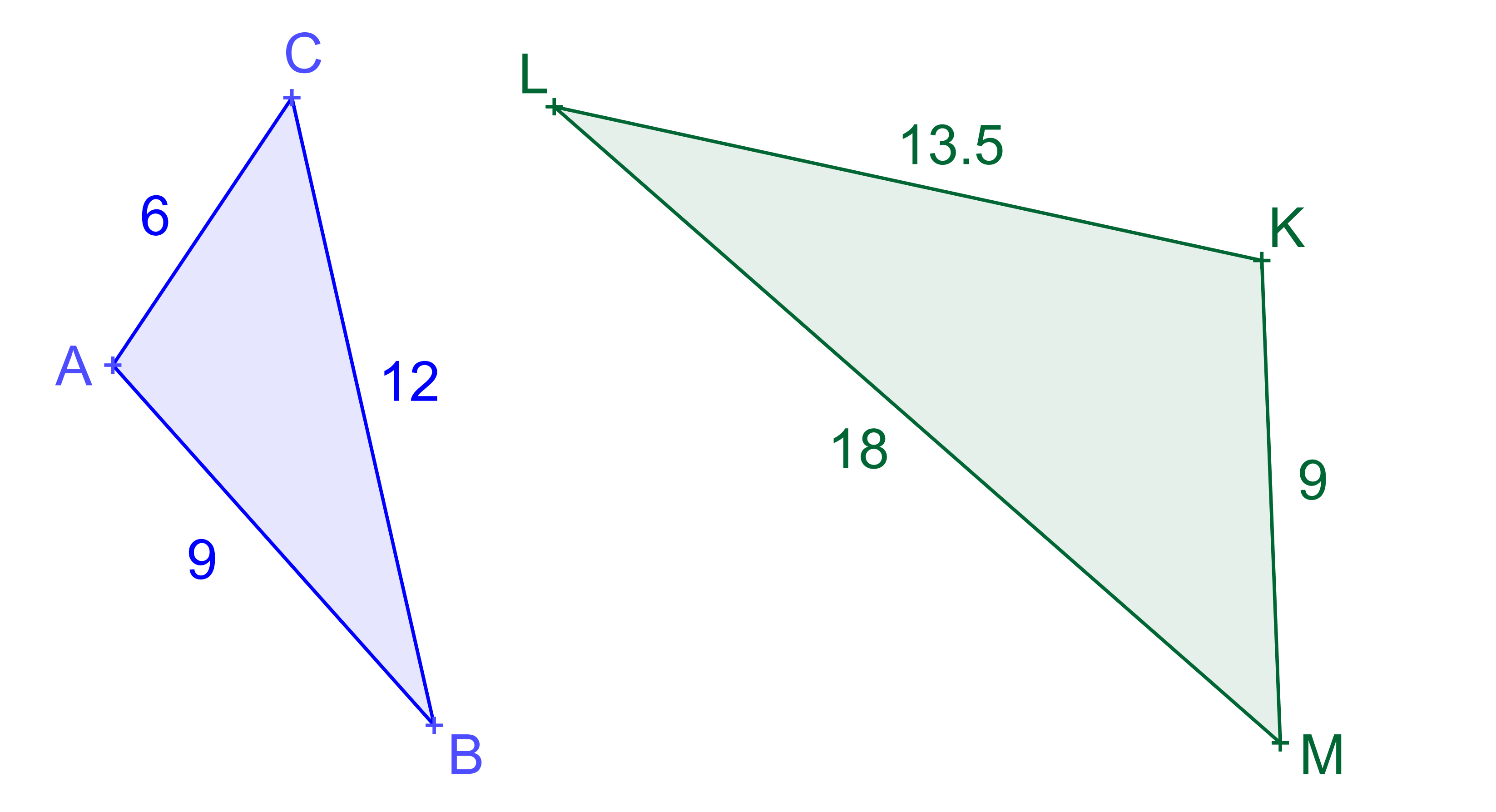
  Kapitola 14 Podobné útvary. ÚKOL: Zdůvodněte podobnost trojúhelníků na obrázku!

  Cvičení:

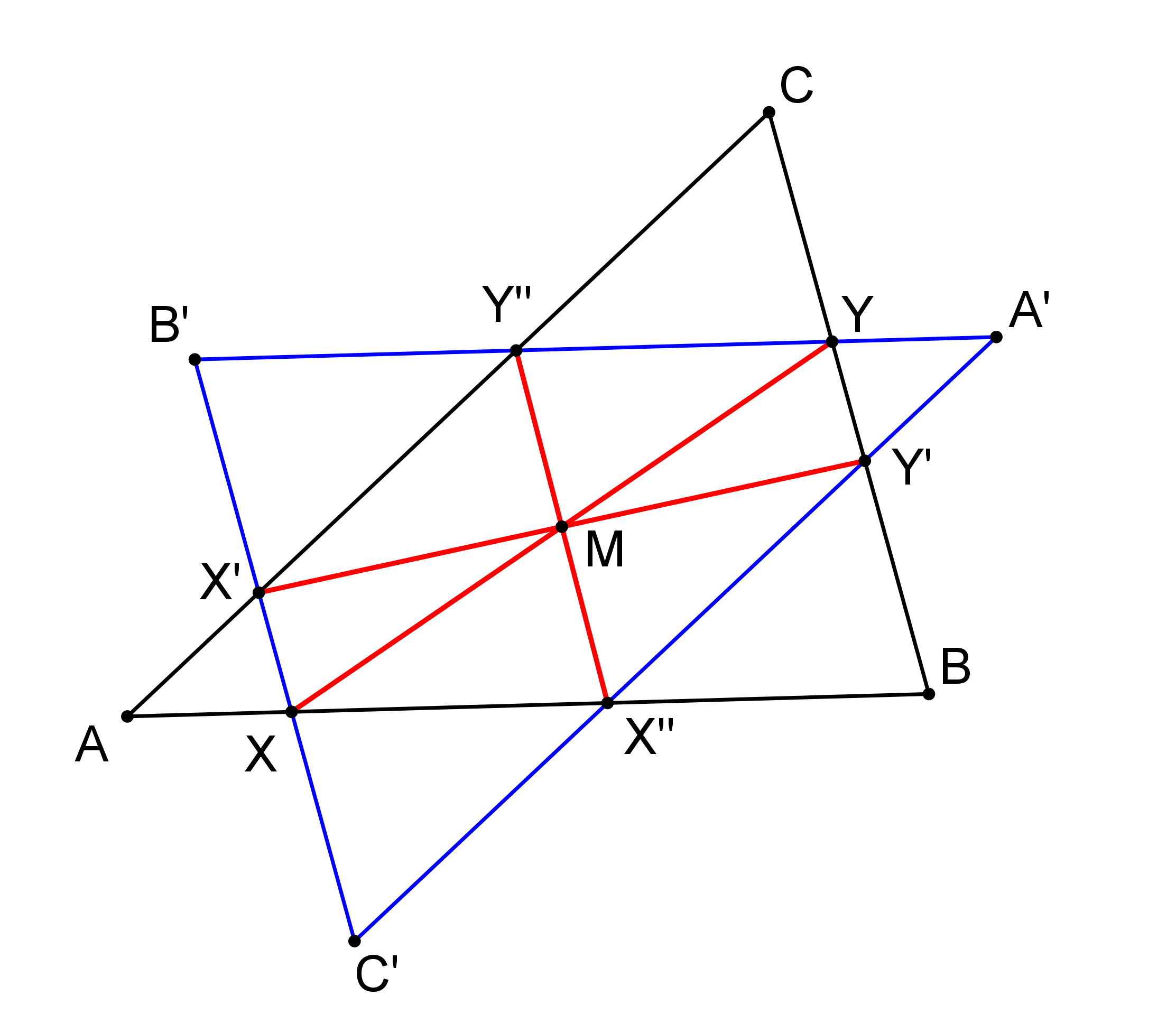
  PŘÍKLAD 13.3. Je dán trojúhelník ABC a jeho vnitřní bod M. Sestrojte všechny úsečky XY se středem M a s krajními body X, Y na hranici trojúhelníku. Řešení: [GeoGebra applet] Detailní popis řešení příkladu je uveden v textu Hašek, R. Planimetrie na str. 59. PŘÍKLAD 13.5. Jsou dány různé rovnoběžné přímky a, b, c a bod A, který leží na přímce a. Sestrojte všechny rovnostranné trojúhelníky ABC,jejichž vrcholy B, C leží po řadě na přímkách b, c. Řešení: GeoGebra applet PŘÍKLAD 14.5. Sestrojte alespoň jeden trojúhelník ABC, pro který platí |AB|:|AC| = 3:5, α = 60°, ρ = 1,8 cm (poloměr kružnice vepsané). Řešení: GeoGebra applet Detailní popis řešení příkladu je uveden v textu Hašek, R. Planimetrie na str. 104. PŘÍKLAD 14.6. Sestrojte kosodélník ABCD, je-li dáno |∠DAB| = α, |∠ABD| = ε, |AC| = e. Řešení: GeoGebra applet Detailní popis řešení příkladu je uveden v textu Hašek, R. Planimetrie na str. 105.

• Věty o podobnosti trojúhelníků.

  J. Verne: Tajuplný ostrov, str. 121-122 (pdf) / J. Verne: Mysterious Island, p. 102-105 (pdf)

  O. Byrne: The Elements of Euclid (B. VI, P. VIII)(1847)

  Přednáška:

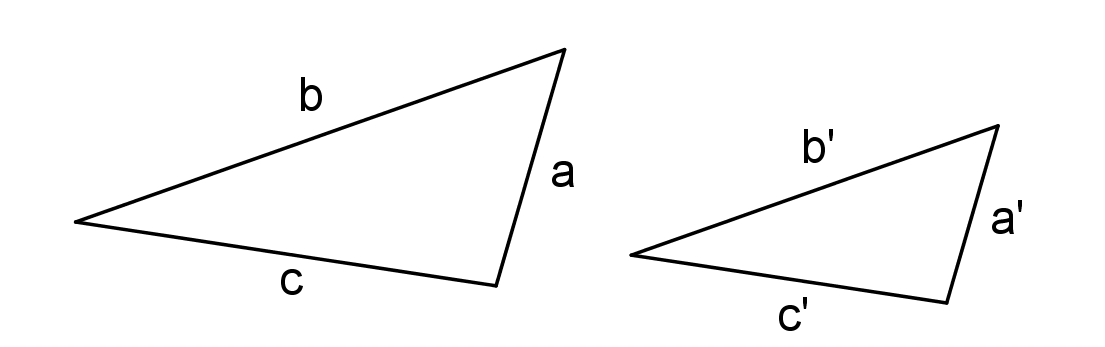
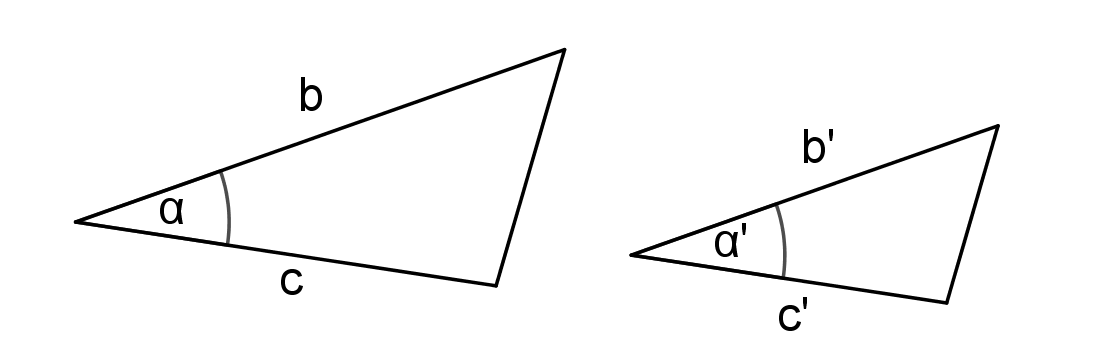
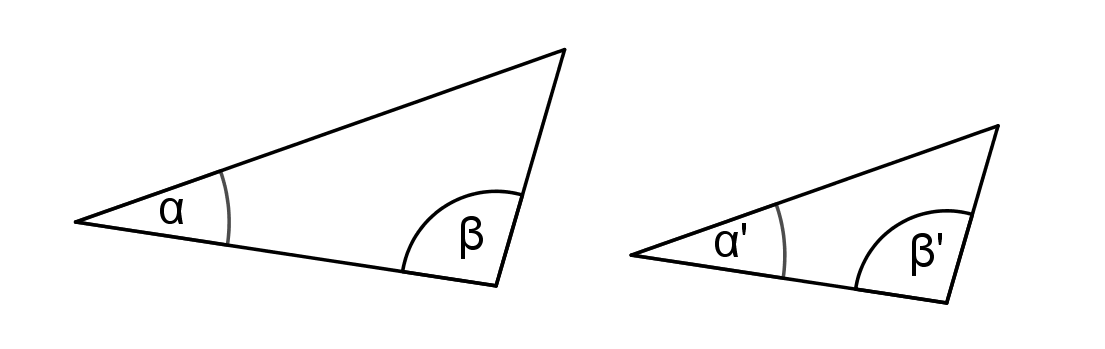
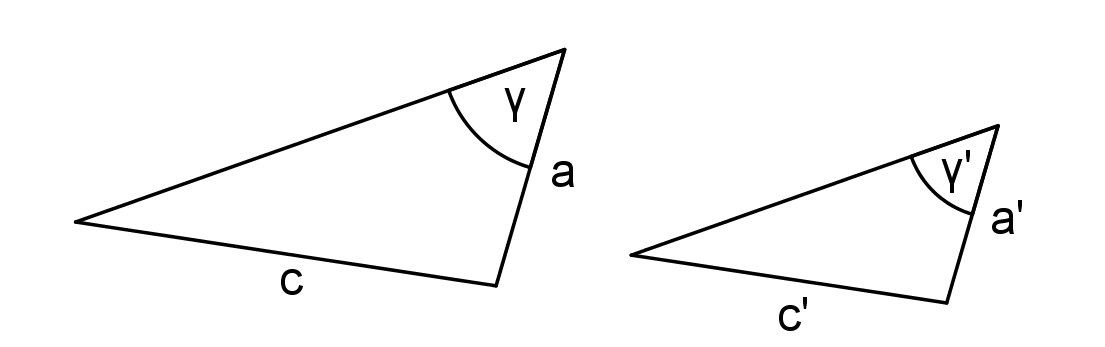
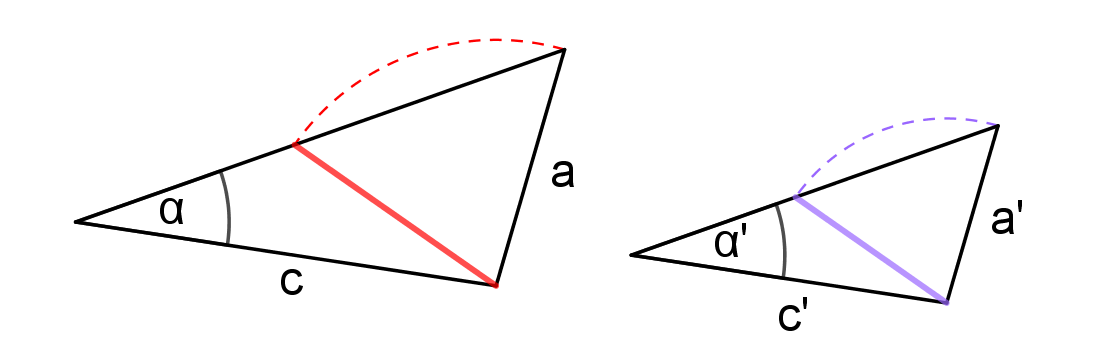
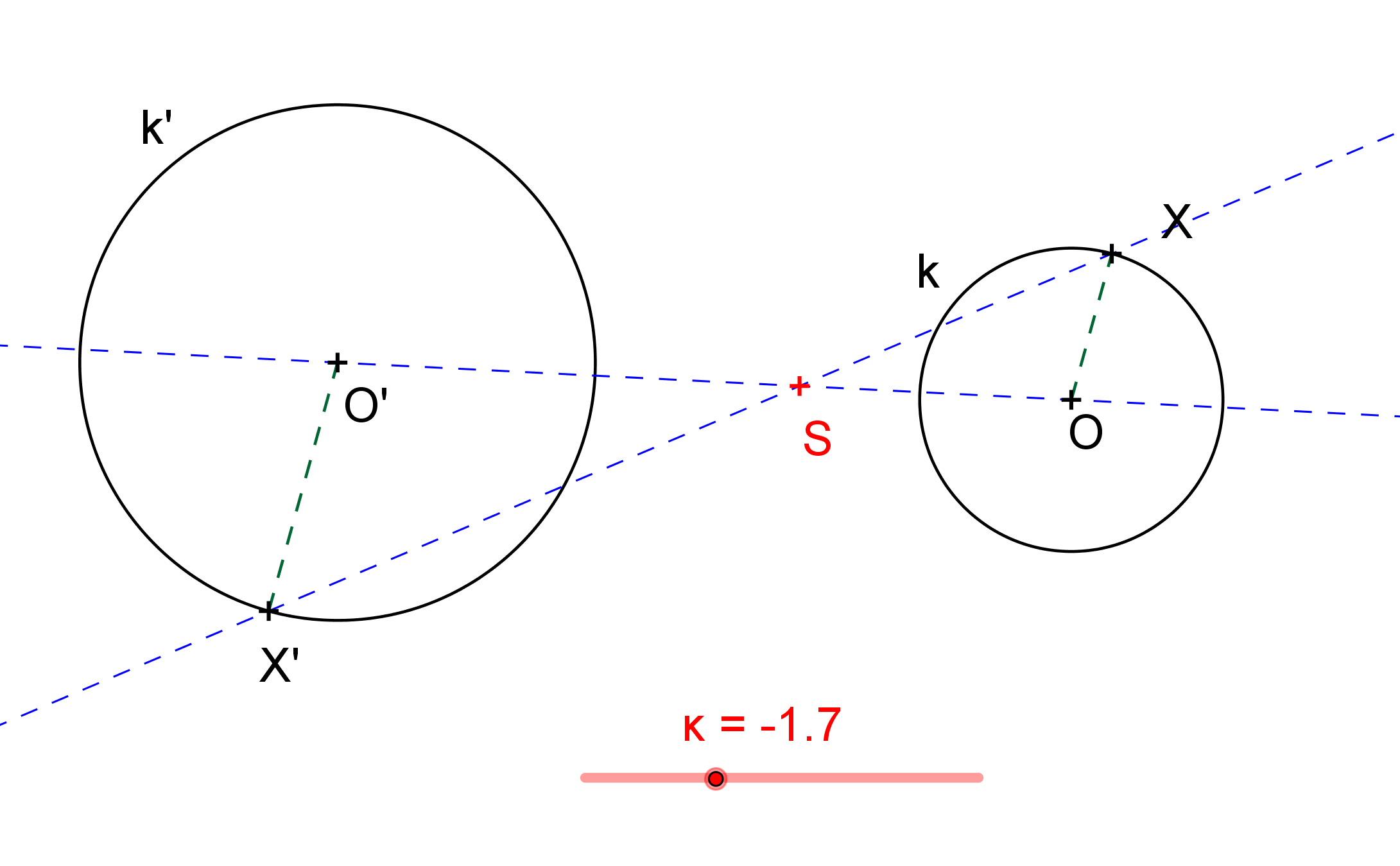
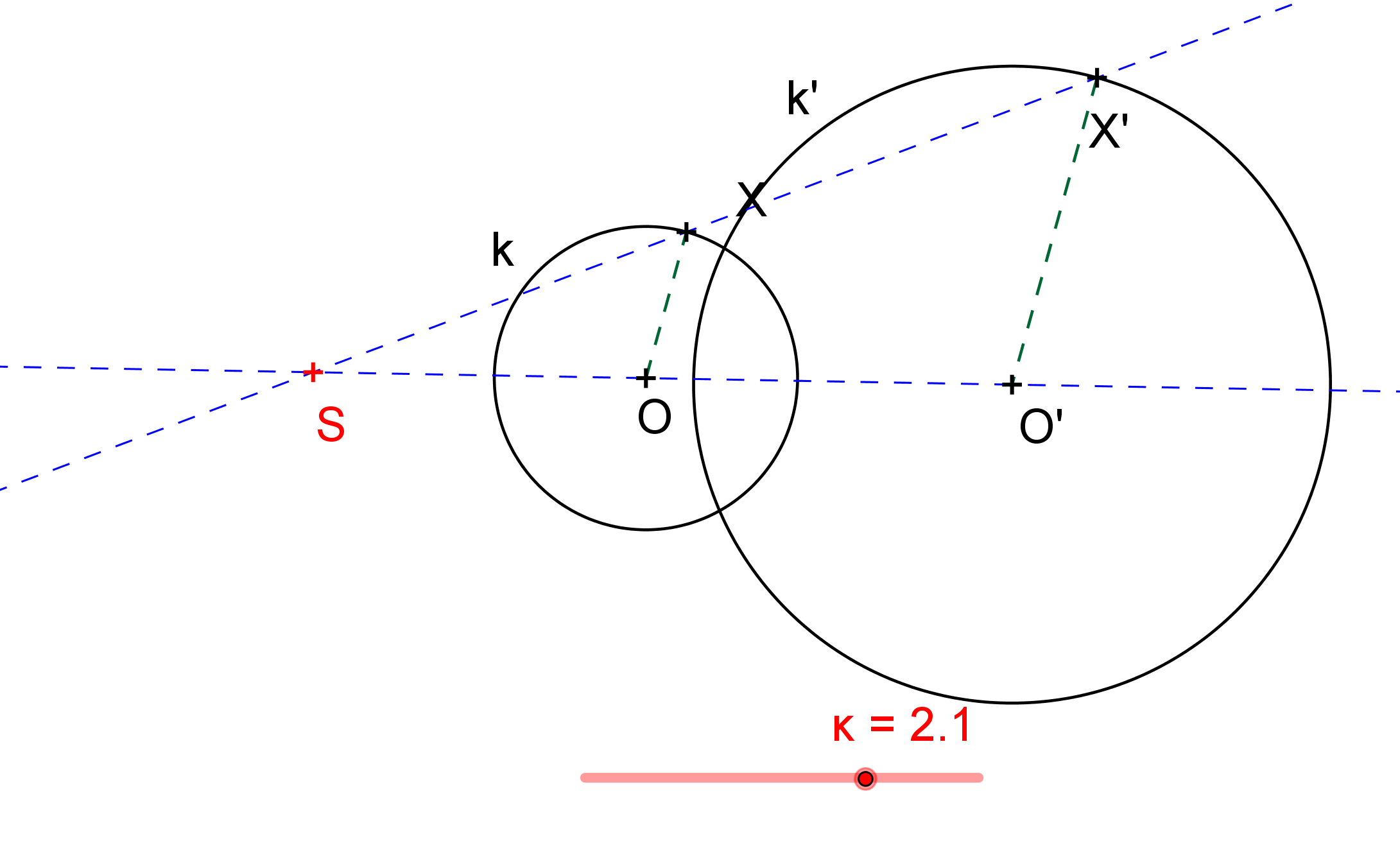
  Kapitola 14 - Podobnost Věty o shodnosti trojúhelníků sss, sus, usu, Ssu Věty o podobnosti trojúhelníků sss, sus, uu, Ssu       Proč nelze uvažovat shodu v úhlu proti menší ze stran? Protože existují dva různé trojúhelníky, které se shodují ve dvou stranách a úhlu proti měnší z nich! Kapitola 15 - Stejnolehlost GeoGebra applet: Stejnolehlost Zobrazení kružnice ve stejnolehlosti   [GeoGebra applet: Zobrazení kružnice ve stejnolehlosti] Určení středů stejnolehlostí dvou kružnic Každé dvě kružnice jsou stejnolehlé; existují jedna, většinou však dvě stejnolehlosti, v nichž se jedna zobrazí na druhou. Zajímá nás, jak určíme středy těchto stejnolehlostí. Koeficenty jsou jasné, jejich absolutní hodnota je rovna poměru poloměrů příslušných kružnic, v pořadí obraz - vzor.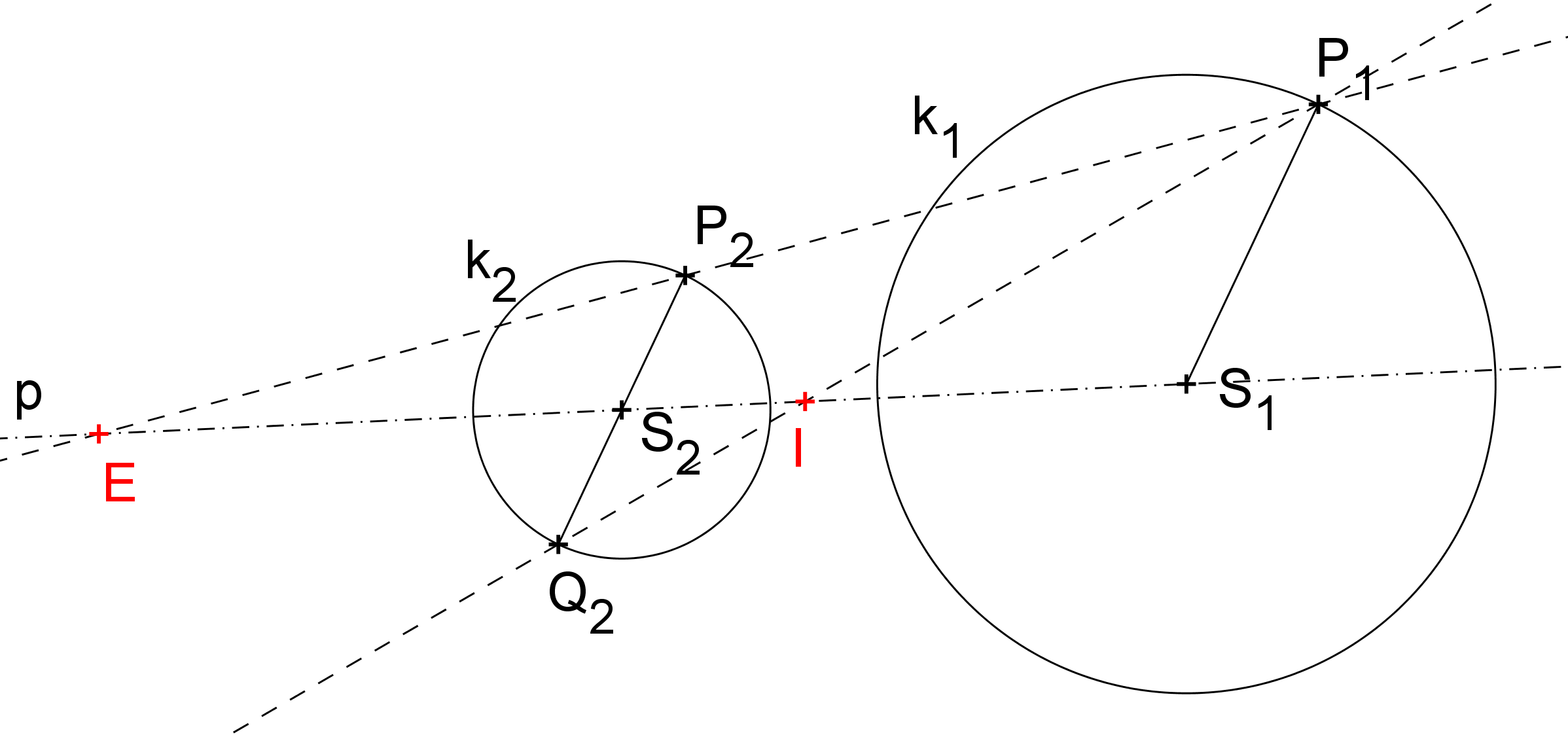 [GeoGebra applet: Určení středů stejnolehlostí dvou kružnic] Konstrukce společných tečen dvou kružnic Společné tečny kružnic procházejí středy jejich stejnolehlostí, vnější tečny středem E, vnitřní tečny středem I. Stačí tedy najít tyto středy a potom sestrojit tečny z každého z nich k jedné z daných kružnic (užitím Thaletovy kružnice), automaticky budou tečnami i druhé kružnice.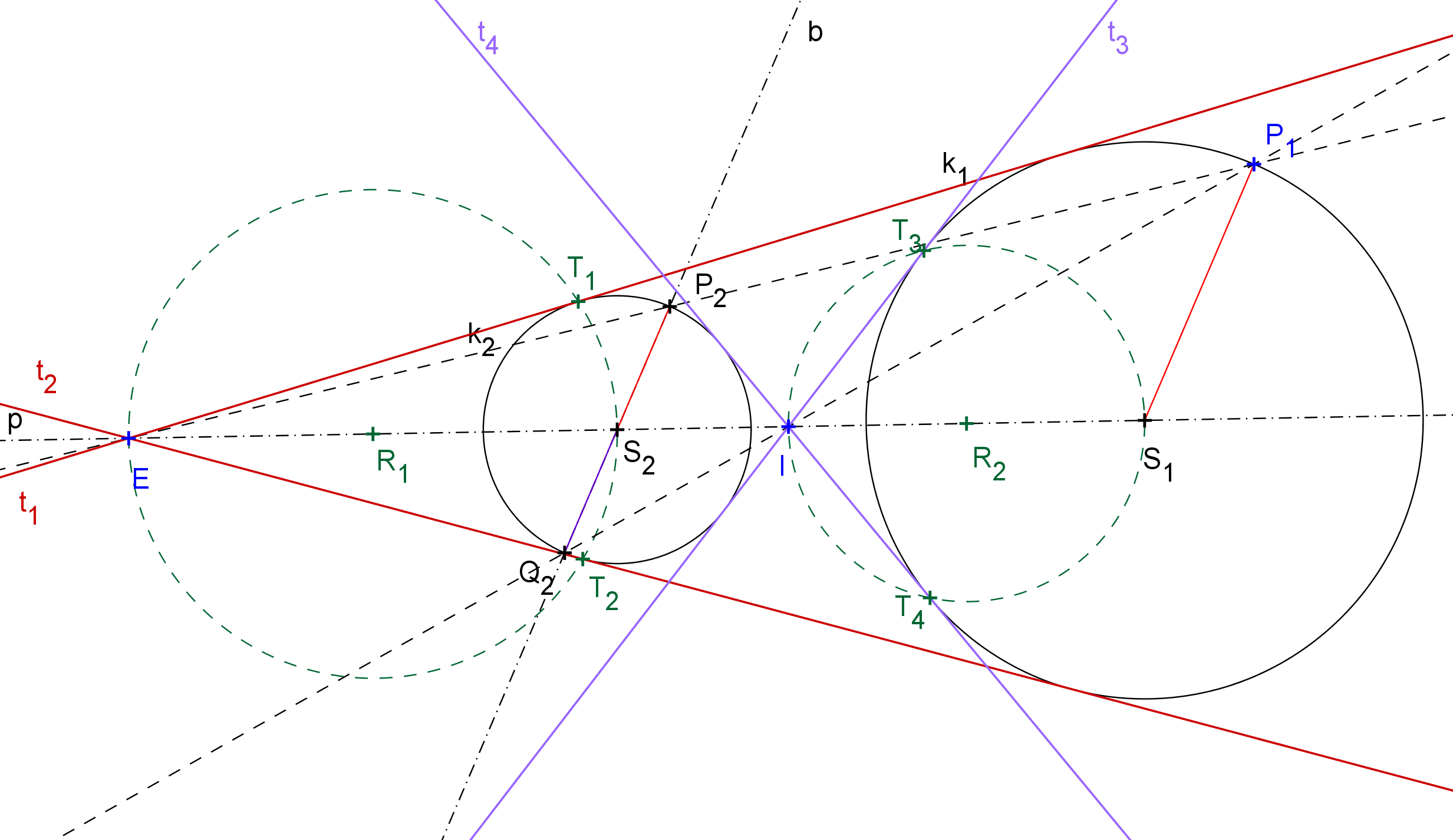 [GeoGebra applet: Konstrukce společných tečen dvou kružnic]

  Cvičení:

  ÚKOL: Vyhlédněte si nějakou vysokou stavbu, sochu či strom a s užitím podobnosti trojúhelníků určete její výšku. Vytvořte fotografickou dokumentaci (alespoň jeden snímek) a své výpočty i s postupem zapište.

Materiály k přednáškám

[Eukleidovské konstrukce]
[Kosý šestiboký hranol (GeoGebra aplet)] [Kolmý pětiboký hranol (GeoGebra aplet)]
[Pravidelné mnohostěny (prezentace v pdf)]
[Cavalieriho princip (GeoGebra aplet)]
[Symmetry in Geometry (Video)]
[GeoGebra aplet: Stejnolehlost]
[Elica (volně dostupný soubor aplikací především pro podporu stereometrie)]
[Paper models of polyhedra: http://www.korthalsaltes.com]

Literatura

[1] Odvárko, O., Kadleček, J. Přehled matematiky pro ZŠ a víceletá gymnázia. Prometheus, Praha, 2004.
[2] Kuřina, F. 10 geometrických transformací. Prometheus, Praha, 2002.
[3] Kuřina, F. 10 pohledů na geometrii. Akademie věd České republiky, 1996.
[4] Polák, J. Přehled středoškolské matematiky. Prometheus, Praha.
[5] Pomykalová, E. Matematika pro gymnázia - Planimetrie. Prometheus, Praha, 2008.
[6] Pomykalová, E. Matematika pro gymnázia - Stereometrie. Prometheus, Praha, 2014.
[7] Jacobs, H. R. Geometry: seeing, doing, understanding. 3rd ed. New York: W.H. Freeman and Co., 2003.
[8] Voráčová a kol., Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha, 2012.
[9] Vyšín, J. a kol.: Geometrie pro pedagogické fakulty I. díl, SPN, Praha, 1965.
[10] Eukleides, Eukleidovy základy (Elementa), překlad F. Servít, 1907.
Dostupné na https://commons.wikimedia.org/wiki/File:Eukleides_Servit.pdf
[11] učebnice a sbírky úloh pro ZŠ a SŠ.
[12] Fuchs, E., Zelendová, E. Metodické komentáře ke Standardům pro základní vzdělávání: Vzdělávací obor Matematika a její aplikace. NÚV, 2015. [PDF], [https://clanky.rvp.cz/clanek/c/Z/20617/METODICKE-KOMENTARE-K-OBORU-MATEMATIKA-A-JEJI-APLIKACE.html/], str. 74-104.

Internetové odkazy

Software ke stažení

www.geogebra.org ... program GeoGebra (možnost bezplatného stažení)

Materiály pro výuku a sebevzdělávání

Wolfram Demonstrations Project
www.cut-the-knot.org (Interactive Mathematics Miscellany and Puzzles)
http://www.math.uoc.gr (Geometrikon - galerie geometrických témat)

Požadavky na studenta

• Zkouška.
  • Zkouška má dvě části - písemnou a ústní. Předmětem písemné zkoušky je řešení úloh odpovídajících úlohám probíraným na přednáškách a cvičeních. Ústní zkouška je zaměřena na ověření znalosti základních pojmů probíraných na přednáškách.
    Hodnocení písemné části zkoušky:   Písemná část zkoušky může být rozdělena do dvou písemných prací, které se píší v polovině a na konci semestru (řádný termín) nebo může být psána najednou v den konání zkoušky (opravný termín). Maximální bodový zisk z písemné zkoušky činí 48 bodů (v případě rozdělení do dvou písemných prací tedy součet jejich bodových dotací činí těchto 48 bodů). Písemná část zkoušky je ohodnocena známkou, jejíž hodnota závisí na získaném počtu bodů PB tímto způsobem:   0 < PB < 24 ... 4,   24 <= PB < 28 ... 3,   28 <= PB < 33 ... 2-,   33 <= PB < 38 ... 2,   38 <= PB < 43 ... 1-,   43 <= PB <= 48 ... 1. Známka z píselné části zkoušky se promítá do výsledné známky ze zkoušky, ovšem pouze v případě dobrého nebo lepšího hodnocení ústní části zkoušky. Kdo získá z písemné části zkoušky méně než 24 bodů (tj. hodnocení 4), nemůže pokračovat ústní částí zkoušky. Pokud někdo neuspěl v písemných pracích v průběhu semestru, má možnost opakovat celou písemnou práci (v rozsahu učiva celého semestru) při prvním - řádném termínu zkoušky z předmětu KMA/8M1, na který se zapíše. Každý má nárok na jeden řádný termín a dva opravné.
    
    
    [Otázky ke zkoušce KMA/8M1 2022]