Spoření
- Krátkodobé - doba spoření nepřesáhne jedno úrokové období (obvykle 1 rok, předpokládáme roční úrokové období). Úroky jsou připisovány na konci doby spoření. Jednotlivé složky jsou úročeny na základě jednoduchého úročení.
- Dlouhodobé - doba spoření bude delší než jedno úrokové období (předpokládejme roční úrokové období). Úroky se připíší na konci každého úrokového období k naspořené částce a dále se s touto částkou úročí.
Spoření krátkodobé
- Předlhůtní
- Polhůtní
Spoření krátkodobé předlhůtní
- Ukládáme vždy na začátku každé m-tiny roku.
- Chceme zjistit, kolik budou činit úspory i s úroky na konci roku při roční úrokové sazbě i:
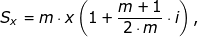kde x je částka, kterou spoříme každou 1/m-tinu roku.
Spoření krátkodobé polhůtní
- Ukládáme vždy na konci každé m-tiny roku.
- Chceme zjistit, kolik budou činit úspory i s úroky na konci roku při roční úrokové sazbě i:
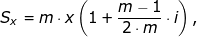kde x je částka, kterou spoříme každou 1/m-tinu roku.
Spoření dlouhodobé
- Spoříme několik úrokových období.
- V rámci úrokového období spoříme pouze jednou.
- Úrokové období je jeden rok.
- Předlhůtní.
- Polhůtní.
Spoření dlouhodobé předlhůtní
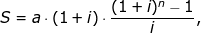kde
| S | ... | naspořená částka, |
| a | ... | výše úložky, která je ukládána vždy na počátku úrokového období (roku), |
| i | ... | roční úroková sazba, |
| n | ... | počet úrokových období, v kterých se spoří. |
Střadatel předlhůtní - udává, kolik ušetříme za n období při úrokové sazbě i, jestliže na počátku každého období uložíme 1 Kč:
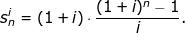
Spoření dlouhodobé polhůtní
Částky ukládáme na konci úrokového období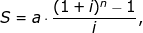
kde
| S | ... | naspořená částka, |
| a | ... | výše úložky, která je ukládána vždy na konci úrokového období (roku), |
| i | ... | roční úroková sazba, |
| n | ... | počet období (let) spoření. |
Střadatel polhůtní - udává, kolik ušetříme za n období při úrokové sazbě i, jestliže na konci každého období uložíme 1 Kč:
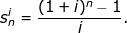Střadatel předlhůtní = (1+i) · Střadatel polhůtní
Kombinace krátkodobého a dlouhodobého spoření
- Spoříme n období.
- Ukládáme m-krát za úrokové období.
- Předlhůtní.
- Polhůtní.
Kombinace krátkodobého a dlouhodobého spoření při spoření předlhůtním
? Kolik uspoříme do konce n-tého roku, ukládáme-li na počátku každé m-tiny roku x Kč?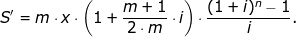
Kombinace krátkodobého a dlouhodobého spoření při spoření polhůtním
? Kolik uspoříme do konce n-tého roku, ukládáme-li na konci každé m-tiny roku x Kč?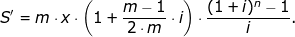
Řešené úlohy
Úloha 1
Kolik budeme mít k dispozici na účtu za tři roky, jestliže na počátku 1.roku uložíme částku 20 000 Kč a koncem každého měsíce spoříme na tento účet 1 000 Kč? Úroková sazba je 2,5% p.a. s pololetním připisováním úroků.
| Tutorial | Tutorial(PDF) |
Úloha 2
Jak dlouho je nutno spořit počátkem každého měsíce 500 Kč, aby uspořená částka byla ve výši 50 000 Kč při neměnné 3%-ní roční úrokové sazbě a ročním připisování úroků?
| Tutorial | Tutorial(PDF) |
Úloha 3
Členové bytového družstva se dohodli, že za 5 let udělají novou střechu (počet bytových jednotek je 12). Na pokrytí části předpokládaných nákladů zřídili účet v bance úročený 2% p.a. Fond se bude vytvářet tak, že koncem každého měsíce bude na společný účet zaslána částka 1000Kč za každou bytovou jednotku . Za předpokladu, že všichni tento plán dodrží
- určete, jaké výše dosáhne fond za 5 let,
- zjistěte, jak by se výsledná částka změnila, kdyby po 2 letech vyčerpali z fondu jednorázově 100 000 Kč, ale pak pokračovali v jeho vytváření beze změn?
Předpokládejme roční úrokové období.
| Tutorial | Tutorial(PDF) |
Úloha 4
Při stavebním spoření se spoří se státní podporou. Jestliže např. měsíční vklad činí 1700 Kč, pak se vždy 1. dubna následujícího roku připíše k naspořené částce státní příspěvek ve výši 3 000 Kč (státní příspěvek za poslední šestý rok je připsán rovnou na konci šestého roku). Jaké výše dosáhne naspořená částka po 6 letech, jestliže stavební spořitelna používá úrokovou míru 2% p.a. s měsíčním připisováním.
| Tutorial | Tutorial(PDF) |