PLANIMETRIE - KMA/PLA

Předmět Planimetrie je věnován detailnímu seznámení s afinními transformacemi roviny, především se shodnostmi a podobnostmi, a s jejich použitím v konstrukčních úlohách.

Kompletní učební text ve formátu PDF: Hašek: PLANIMETRIE - KMA/PLA (aktualizováno 9. 4. 2018).

Osnova předmětu

• Afinní zobrazení. Afinní transformace roviny.

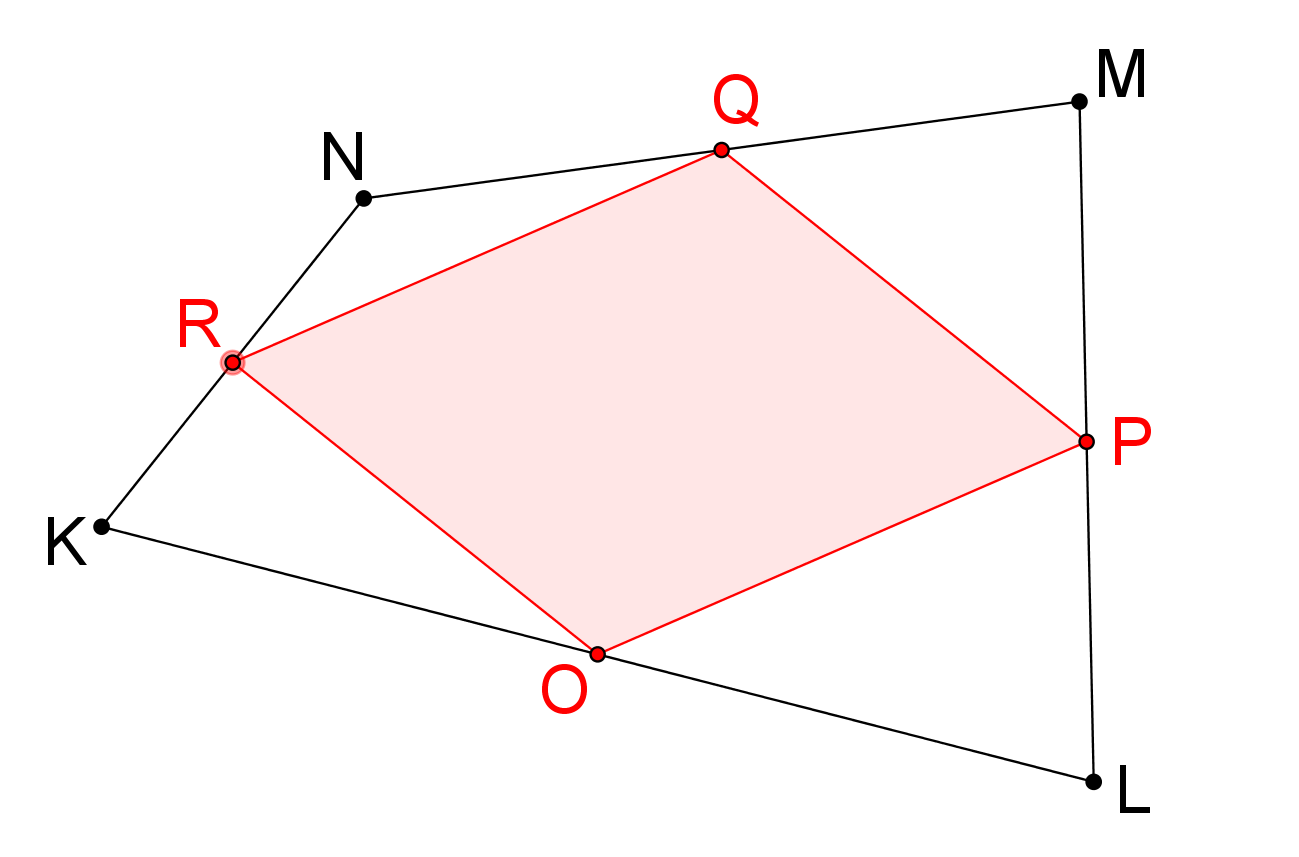
  CVIČENÍ 1 Zaregistrujte se na stránce geogebra.org a nainstalujte si na svůj počítač program GeoGebra. Varignonova věta: Středy stran libovolného čtyřúhelníku tvoří rovnoběžník. (Pierre Varignon, 1654-1722) Příklad 1: Užitím programu GeoGebra sestrojte libovolný čtyřúhelník KLMN a středy jeho stran O, P, Q, R. Ověřte pravdivost tvrzení Varignonovy věty a pokuste se ji dokázat. Potom vyslovte hypotézu o vztahu obsahů čtyřúhelníku KLMN a rovnoběžníku OPQR. Prémiový úkol č. 0: Uvažujte Varignonovu větu. Dokažte, že obsah uvedeného čtyřúhelníku je dvojnásobkem obsahu rovnoběžníku tvořeného středy jeho stran. (Podmínky řešení prémiových příkladů viz Požadavky)

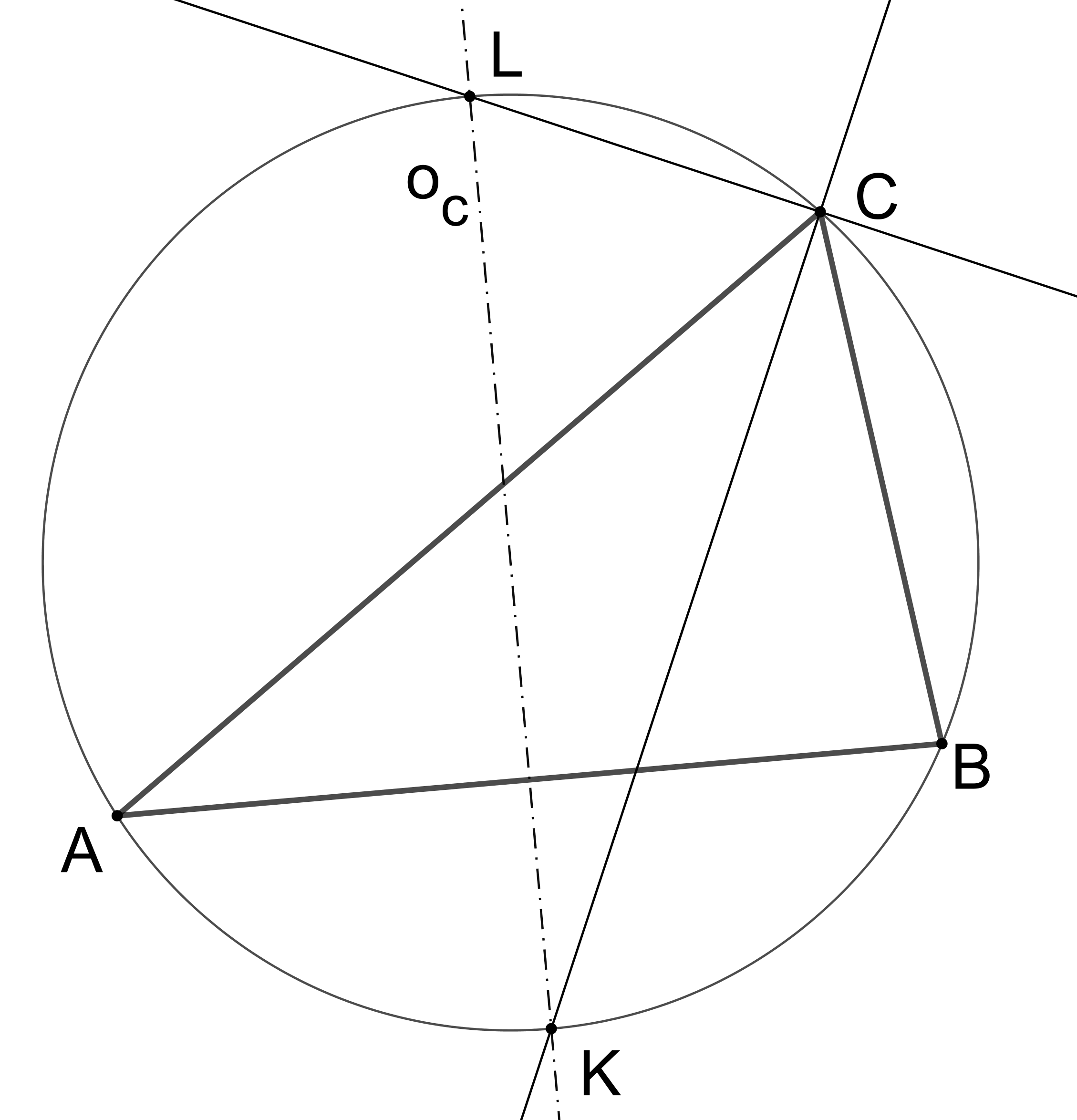
  PŘEDNÁŠKA 1 Úvod. Zopakování základních pojmů. Geometrická zobrazení. Příklad 1:  Pomocí programu GeoGebra vyzkoumejte, zda se v následujících zobrazeních zobrazí střed úsečky zase na střed úsečky: stejnolehlost, osová afinita, středová kolineace, kruhová inverze. Využijte aplety s ukázkami uvedených zobrazení: [Stejnolehlost] [Osová afinita] [Středová kolineace] [Kruhová inverze] Prémiový úkol č. 1:  Pro libovolný trojúhelník ABC protíná osa Oc jeho strany AB kružnici trojúhelníku opsanou v bodech K a L, viz obrázek. Dokažte, že přímka CK je osou vnitřního úhlu tohoto trojúhelníku při vrcholu C, zatímco přímka CL je osou vnějšího úhlu trojúhelníku při vrcholu C. (Podmínky řešení prémiových příkladů viz Požadavky)

  CVIČENÍ 2 (Geometrické zobrazení, Dělicí poměr) Příklad 1: Přímka p je dána body A a B. Jaký je rozdíl v tom, když určíme polohu bodu C na této přímce a) jeho vzdálenostmi od bodů A, B, b) poměrem jeho vzdáleností od bodů A, B. Příklad 2: V rovině jsou dány dva pevné body A a B. Určete množinu všech bodů X této roviny, pro které platí |AX|/|BX|=k, kde k je reálná konstanta. Použijte program GeoGebra, modelujte v něm zadání, pokuste se vykreslit příslušnou křivku a určit její rovnici. Domácí úkol č. 1: Na volný papír narýsujte trojúhelník ABC, sestrojte jeho výšky a jejich průsečík označte O (ortocentrum). Potom postupně zobrazte bod O v osových souměrostech s osami AB, BC a CA. Vyslovte hypotézu o polohách těchto bodů.

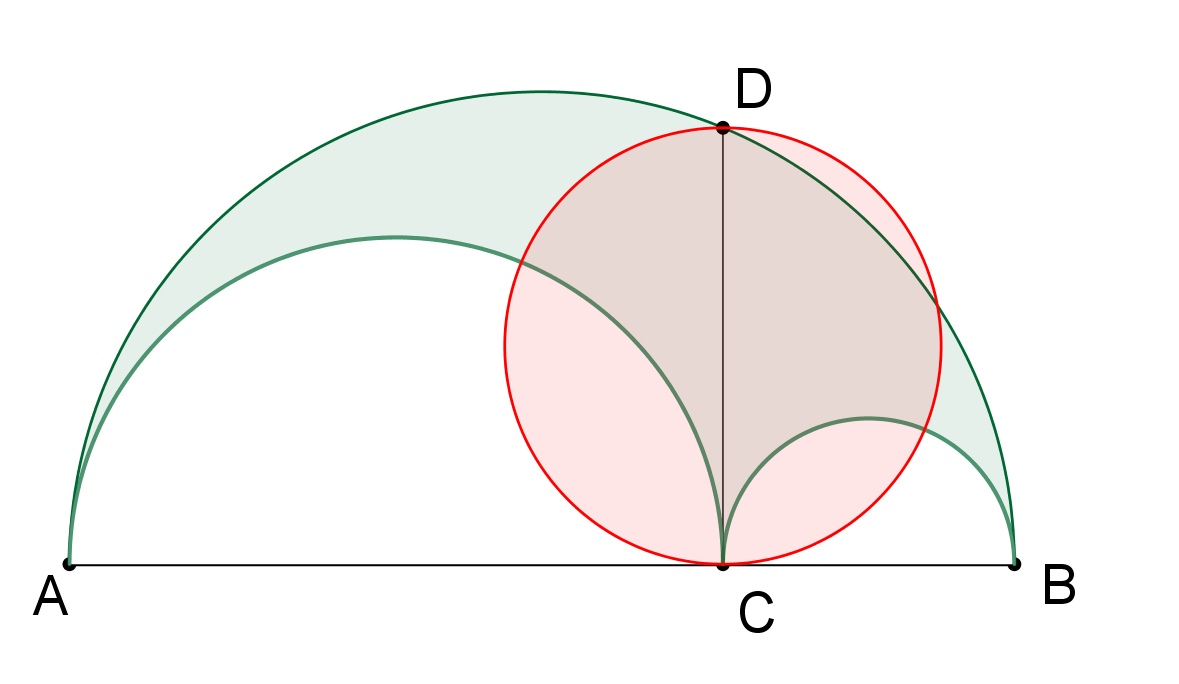
  PŘEDNÁŠKA 2 Afinní zobrazení. Dělicí poměr. Příklad 1: Určete dělicí poměr (ABS) středu S úsečky AB vzhledem k jejím krajním bodům A, B. Prémiový úkol č. 2:  Do půlkruhu s průměrem AB jsou vepsány půlkruhy s průměry AC a CB, z bodu C je potom vedena kolmice protínající hraniční půlkružnici v bodě D, viz obrázek. Dokažte, že obsah zelené plochy v obrázku je roven obsahu červeného kruhu s průmerem CD.

  CVIČENÍ 3 (Rovnice afinního zobrazení) Řešení příkladu 2 z cv. 2: V rovině jsou dány dva pevné body A, B. Určete množinu všech bodů X této roviny, pro které platí |AX|/|BX|=k, kde k je reálné číslo. [Řešení v GeoGebře] Hypotéza plynoucí z domácího úkolu č. 1 a její důkaz: (Na volný papír narýsujte trojúhelník ABC, sestrojte jeho výšky a jejich průsečík označte O (ortocentrum). Potom postupně zobrazte bod O v osových souměrostech s osami AB, BC a CA. Vyslovte hypotézu o polohách těchto bodů.) Vztah mezi velikostí obvodového a středového úhlu: Velikost obvodového úhlu příslušejícího oblouku AB je rovna polovině velikosti středového úhlu příslušejícího témuž oblouku. [GeoGebra aplet] Tětivový čtyřúhelník: Čtyřúhelník vepsaný do kružnice, součet jeho protilehlých úhlů je 180° (viz Wikipedia: Cyclic quadrilateral).

• Shodná zobrazení v rovině. Analytické vyjádření shodností.

  PŘEDNÁŠKA 3 Afinní transformace roviny - Afinita. [Afinní transformace roviny: "Úprava" fotografie] Shodná zobrazení v rovině. [Určenost shodnosti v rovině] Příklad 1: V programu GeoGebra sestrojte přímku danou body A a B a libovolně na ní umístěte bod C. Potom tažením myší měňte polohy bodů A, B a sledujte chování bodu C. Co pro něj platí? Své tvrzení podložte výpočtem provedeným v programu. Příklad 2: Pro body A, B, C platí (ABC)=λ. Zapište pomocí λ dělicí poměr (CBA). Domácí úkol č. 2: (Pokračování příkladu 2.) Pro body A, B, C platí (ABC)=λ. Zapište pomocí λ dělicí poměry (BAC), (ACB), (CAB) a (BCA). Domácí úkol č. 3: Pomocí appletu "Úprava" fotografie zapište maticové rovnice následujících zobrazení: (i) osová souměrnost podle osy y, (ii) středová souměrnost podle počátku, (iii) středová souměrnost se středem v bodě [0,5]. 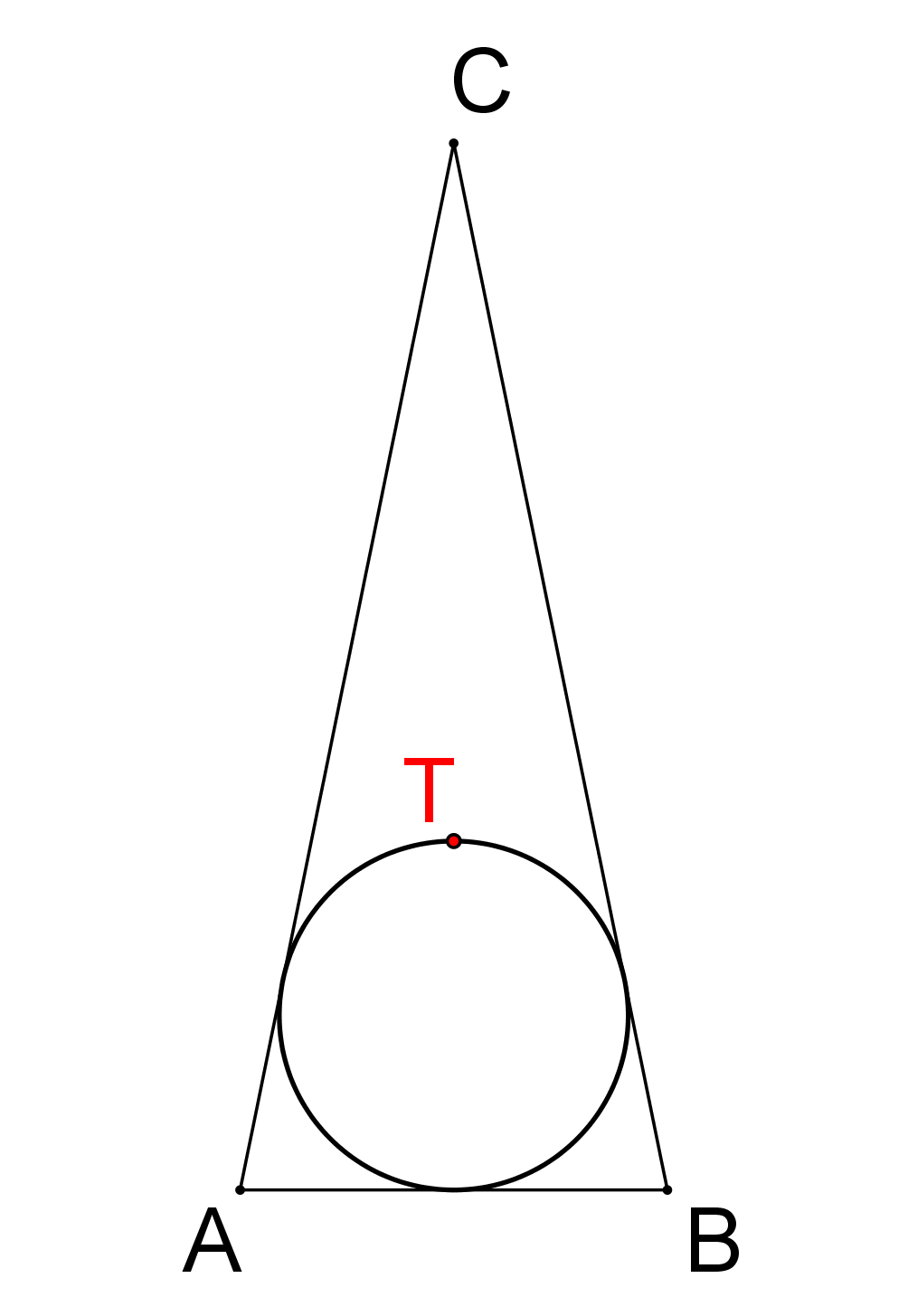Prémiový úkol č. 3:  Kružnice vepsaná rovnoramennému trojúhelníku ABC prochází jeho těžištěm T, viz obrázek. Dokažte, že AC/AB = 5/2.

• Osová souměrnost.

  CVIČENÍ 4 (Osová souměrnost) Příklad 1: Je dána přímka p a body A, B v téže polorovině s hraniční přímkou p. Najděte všechny body X ∈ p takové, že součet vzdáleností |AX|+|BX| je minimální. (Tato úloha je známa jako Heronův problém; Hérón Alexandrijský, přibl. 10-70 n.l.)

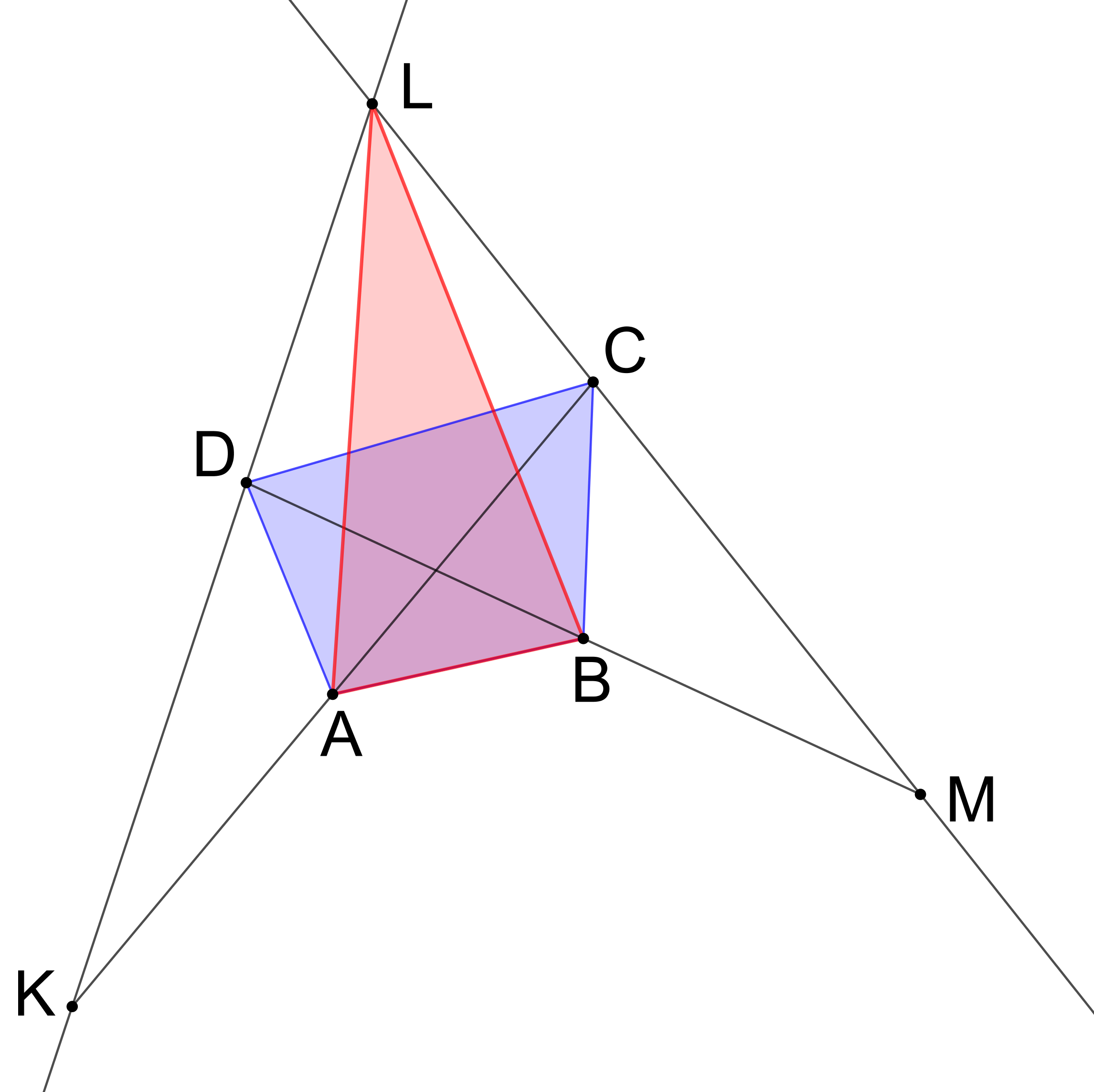
  PŘEDNÁŠKA 4 Analytické vyjádření shodností. [Řešení příkladu 4.2 (samodružné body a směry) v programu wxMaxima] Prémiový úkol č. 4:  Jsou dány různoběžné přímky KL, LM se společným bodem L, viz obrázek. Body C a D potom leží v daném pořadí libovolně na úsečkách LM a KL a body A a B jsou v uvedeném pořadí středy úseček KC a MD. Dokažte, že čtyřúhelník ABCD má stejný obsah jako trojúhelník ABL. [Dynamický obrázek v GeoGebře]

  CVIČENÍ 5 (Osová souměrnost) Vivianiho věta: Součet vzdáleností libovolného bodu v rovnostranném trojúhelníku od jeho stran je roven výšce tohoto trojúhelníku. [en.wikipedia.org: Viviani's theorem] [Dynamický důkaz]

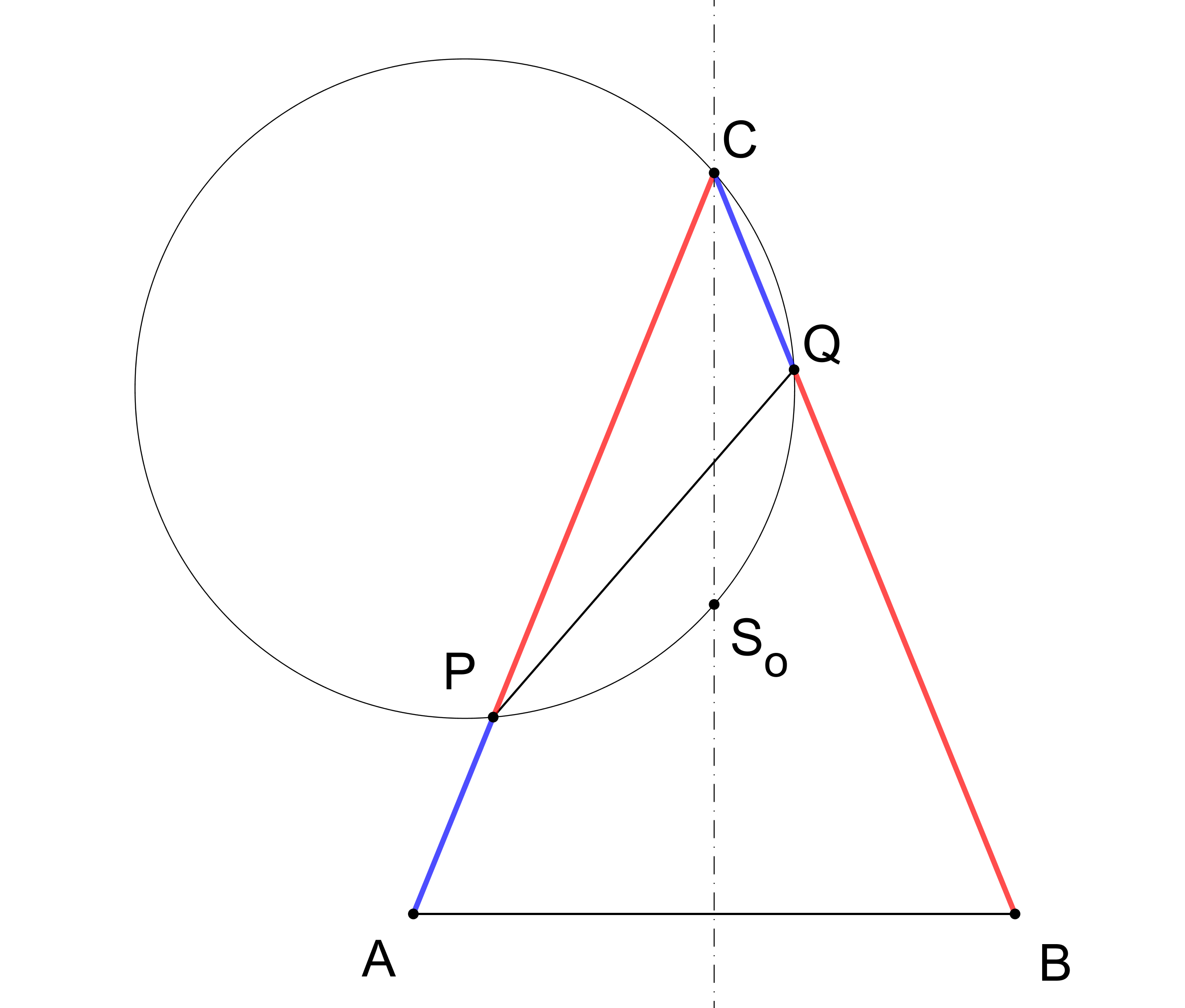
  PŘEDNÁŠKA 5 Analytické vyjádření shodností - Samodružné body a směry Prémiový úkol č. 5:  Na ramenech rovnoramenného trojúhelníku ABC jsou dány body P, Q, různé od vrcholů trojúhelníku, tak, že |PC|=|QB|, viz obrázek. Dokažte, že kružnice opsaná trojúhelníku PQC prochází středem So kružnice opsané trojúhelníku ABC. [Dynamický obrázek v GeoGebře]

  CVIČENÍ 6 (Shodnost. Osová souměrnost.) Příklad 1:  Rozhodněte, zda afinity dané uvedenými rovnicemi jsou shodnosti. Pokud ano, určete jaké (Využijte při tom samodružné body a směry těchto afinit). a) x' = -x + 4, y' = -y - 6, b) x' = x, y' = -y, c) x' = -4/5x + 3/5y + 8, y' = 3/5x + 4/5y - 6. Fermatův bod:  Bod, pro který je součet jeho vzdáleností od vrcholů trojúhelníku minimální. [en.wikipedia.org: Fermat point] [Konstrukce Fermatova bodu] Domácí úkol 2:  Řešte Příklad 1 c.

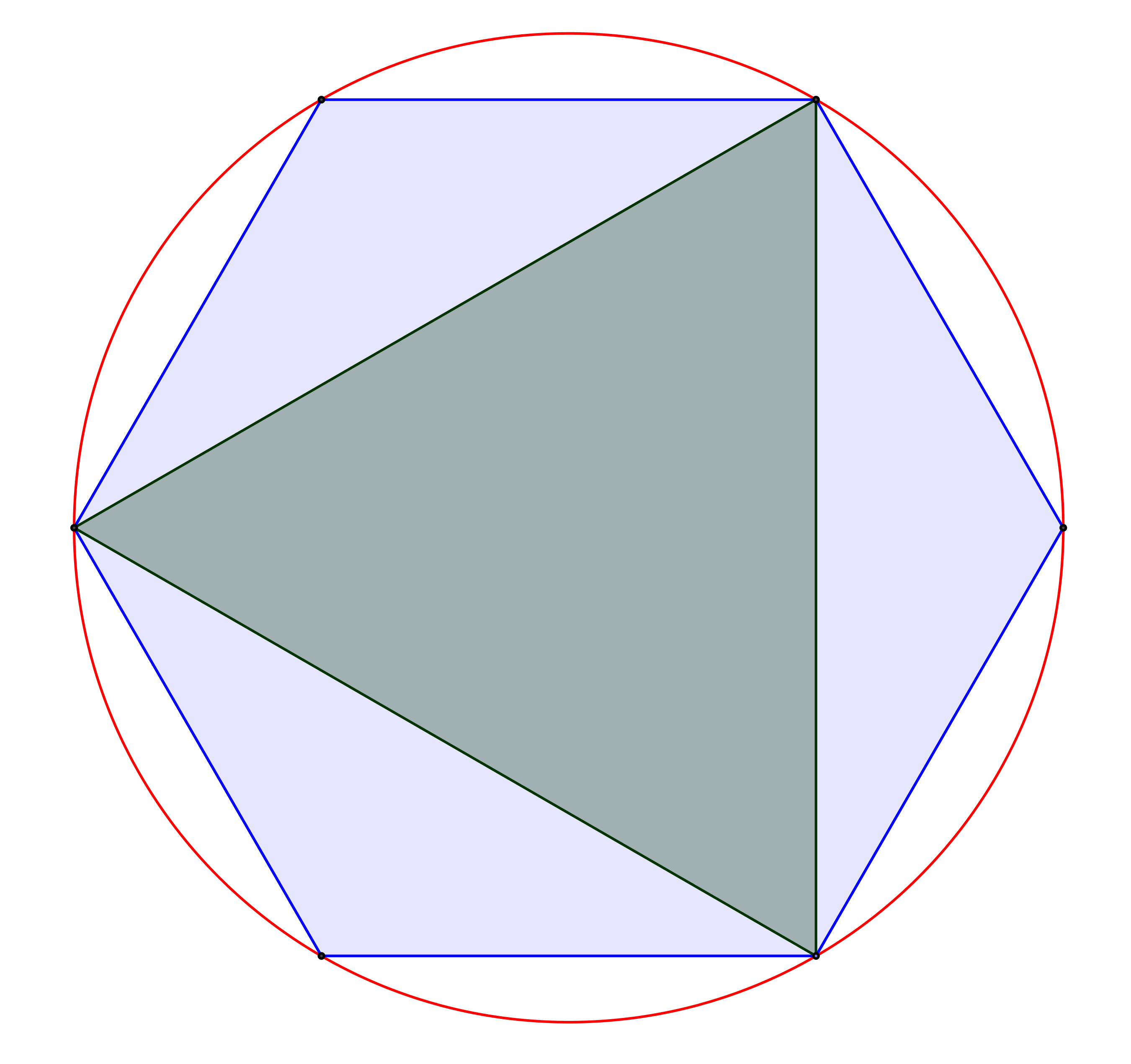
  PŘEDNÁŠKA 6 Osová souměrnost Prémiový úkol č. 6: Do kružnice je vepsán rovnostranný trojúhelník spolu s pravidelným šestiúhelníkem, s kterým má společné vrcholy, viz obrázek. Jaký je poměr jejich obsahů? Své tvrzení dokažte!

• Otočení. Středová souměrnost. Posunutí. Posunuté zrcadlení. Skládání shodností. Shodnosti přímé a nepřímé. Grupa shodností. Klasifikace shodností v rovině.

  CVIČENÍ 7 (Osová souměrnost) Osová souměrnost - úlohy k řešení. Fagnanův problém: Danému ostroúhlému trojúhelníku vepište trojúhelník o nejmenším obvodu. [Fagnanův problém - řešení č. 1] [Fagnanův problém - řešení č. 2]

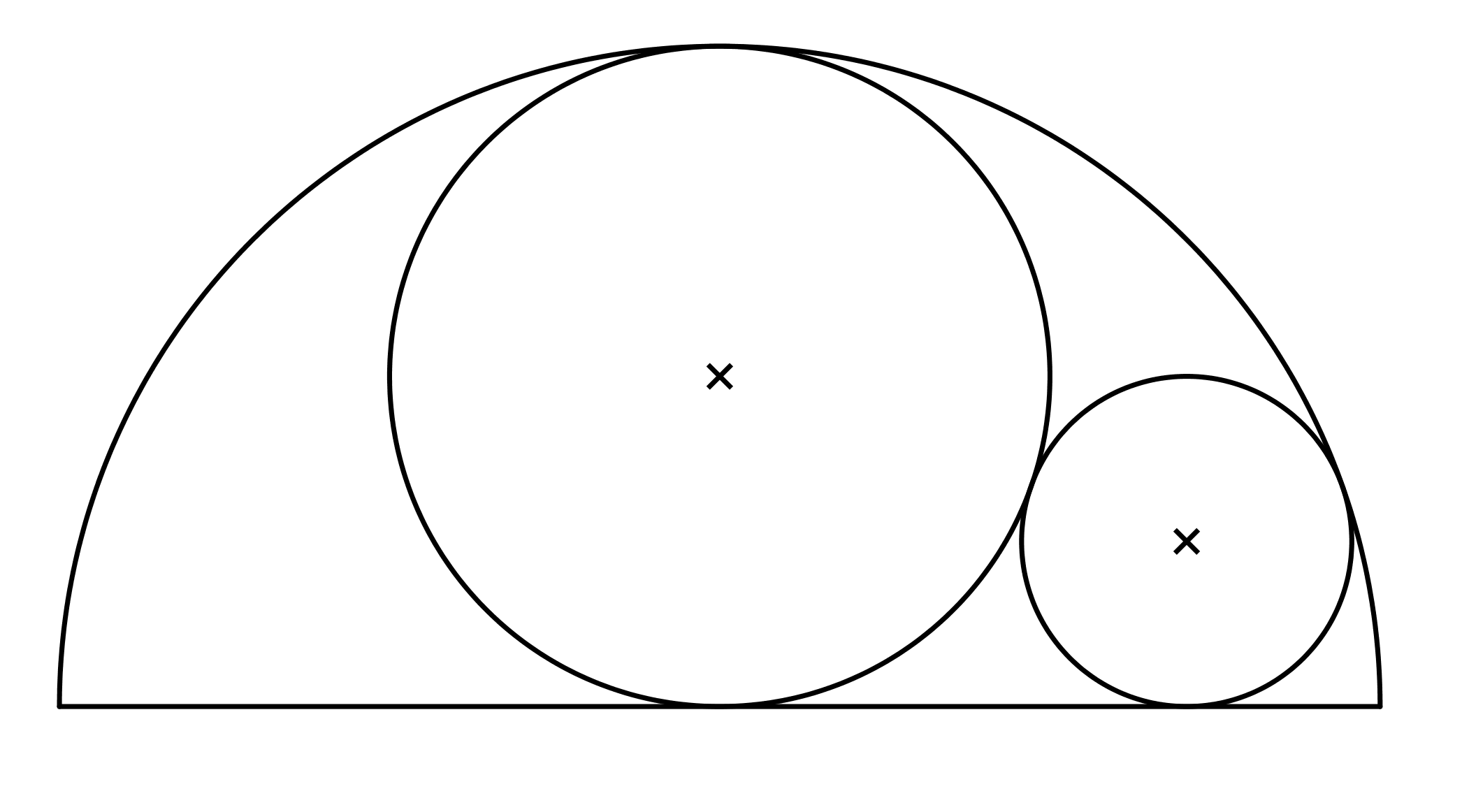
  PŘEDNÁŠKA 7 Osová souměrnost (pokračování). Prémiový úkol č. 7: Do půlkruhu s poloměrem 4 jsou vepsány dva kruhy s průměry 4 a d, které se dotýkají, viz obrázek. Vypočtěte d.

  CVIČENÍ 8 Příklad (Mascheroniova konstrukce): Je dána kružnice k(S;r); dále je dána dvěma body A, B (body neleží na kružnici) její sečna p, která neprochází středem S. Sestrojte průsečíky přímky p s kružnicí k, aniž přitom použijete pravítka. (Lorenzo Mascheroni, 1750-1800, Georg Mohr, 1640-1697, Mascheroni Construction) [Aplet pro provedení konstrukce] [Řešení]

  PŘEDNÁŠKA 8 Otočení. Prémiový úkol č. 8: Uvnitř trojúhelníku ABC je dán bod P. Vedeme-li bodem P rovnoběžky se stranami daného trojúhelníku, dostaneme tři trojúhelníky a tři rovnoběžky, viz obrázek. Dokažte, že součet obsahů těchto tří trojúhelníků je roven alespoň jedné třetině obsahu trojúhelníku ABC.

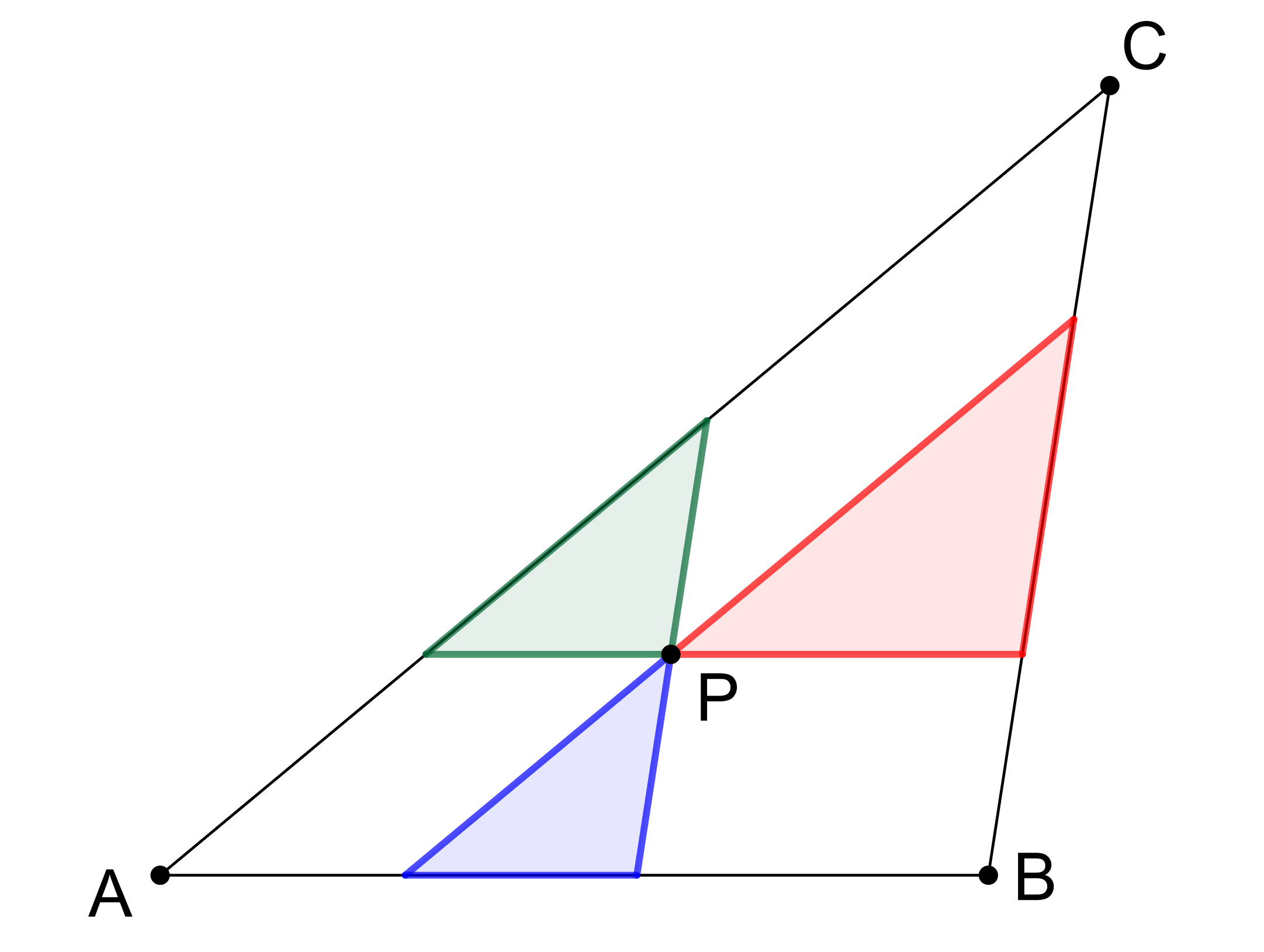
  CVIČENÍ 9 Příklad:  Dokažte následující větu: V každém trojúhelníku dělí osa libovolného vnitřního úhlu protější stranu v poměru stran přilehlých. Otočení - úlohy k řešení. Středová souměrnost - úlohy k řešení.

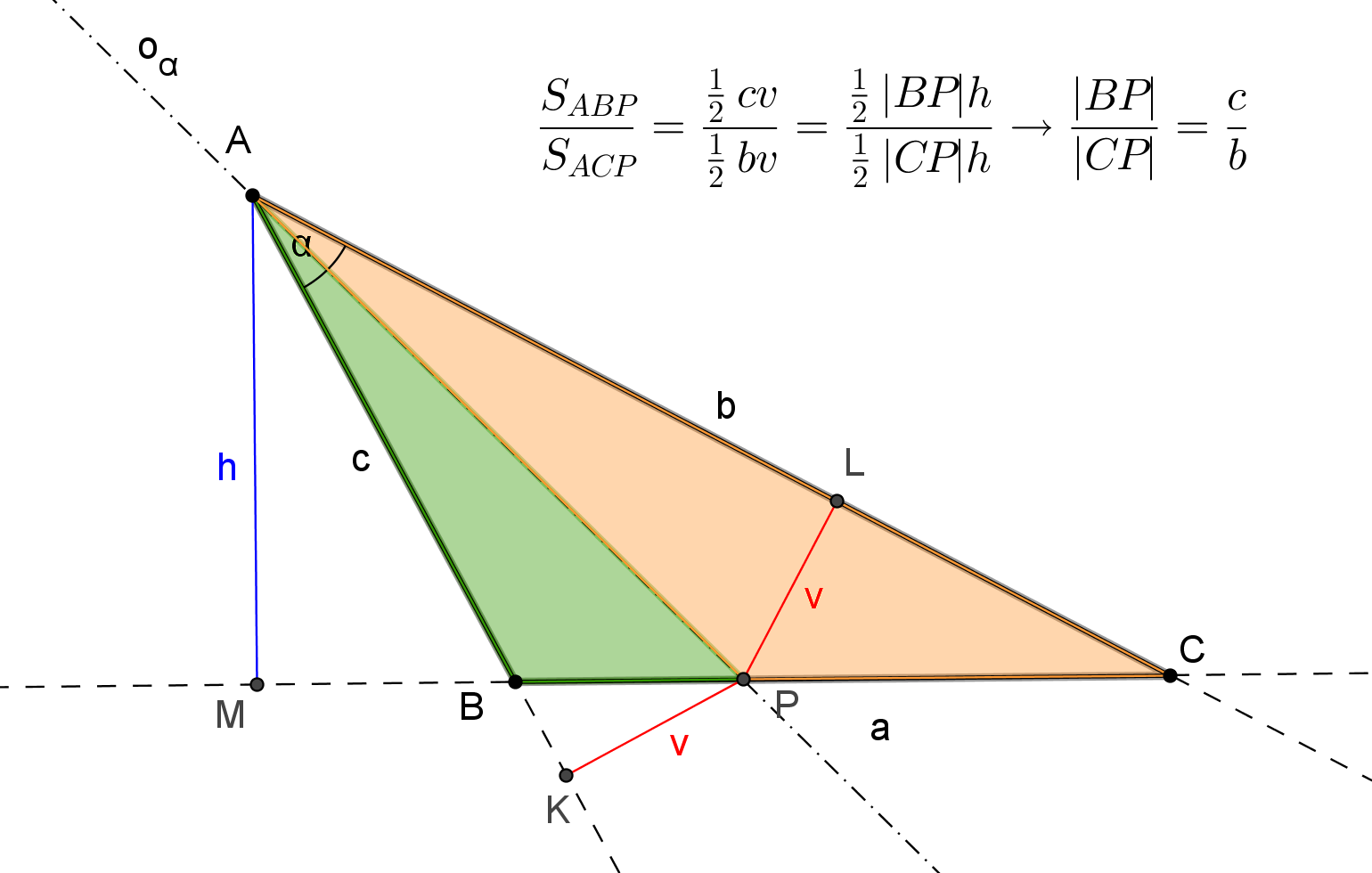
  PŘEDNÁŠKA 9 Středová souměrnost. Úkol: S využitím uvedených apletů promyslete důkaz tvrzení "Každá shodnost se dá složit z nejvýše tří osových souměrností". Aplety: [přímá shodnost][nepřímá shodnost] Posunutí. Posunuté zrcadlení. Prémiový úkol č. 9: Rovnostranný trojúhelník ABC o dělce strany 4 cm otočíme kolem jeho průsečíku výšek o 90°, dostaneme tak trojúhelník A'B'C', viz obrázek. Určete obsah průniku trojúhelníků ABC a A'B'C'.

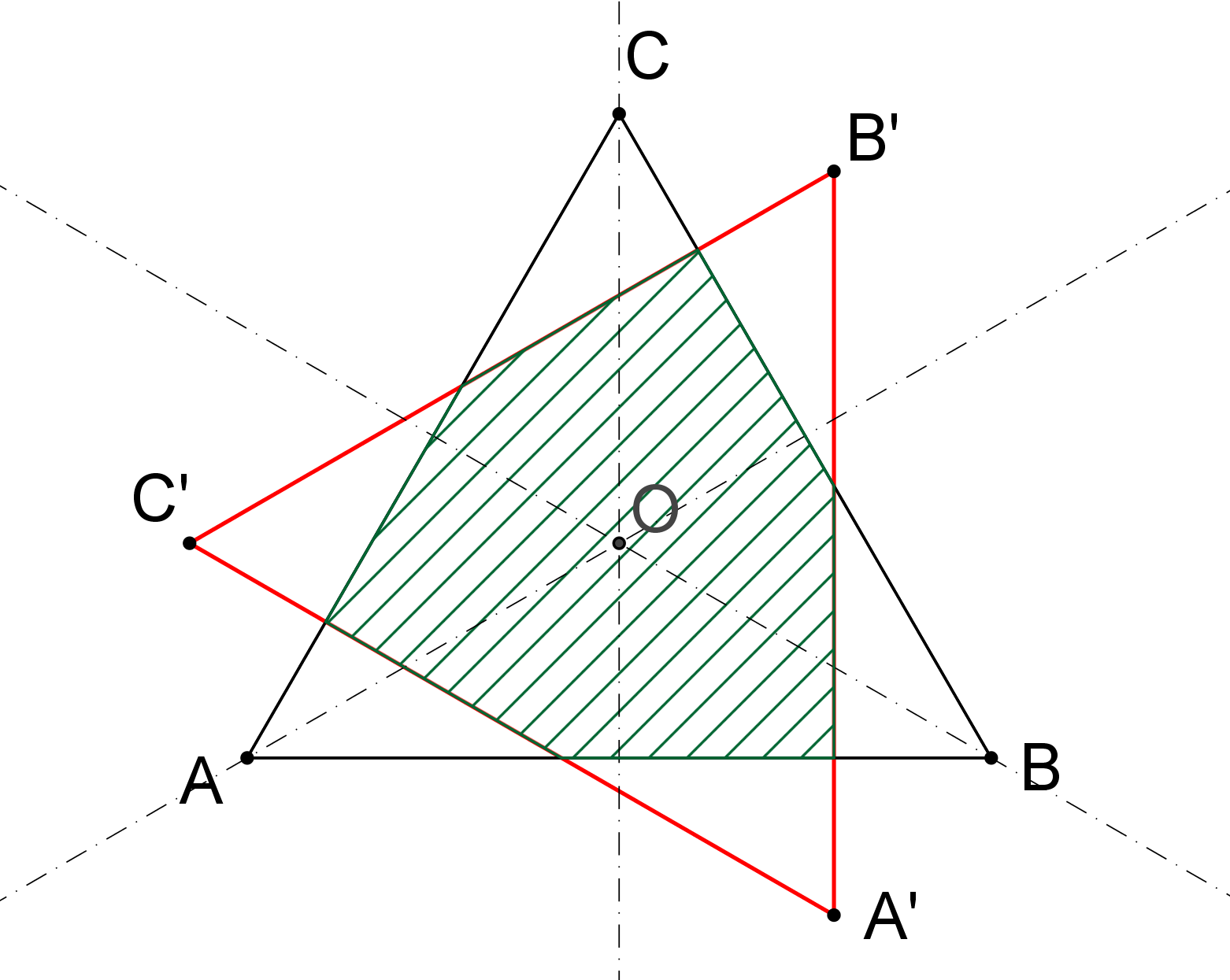
  CVIČENÍ 10 Posunutí - úlohy k řešení. Posunuté zrcadlení.

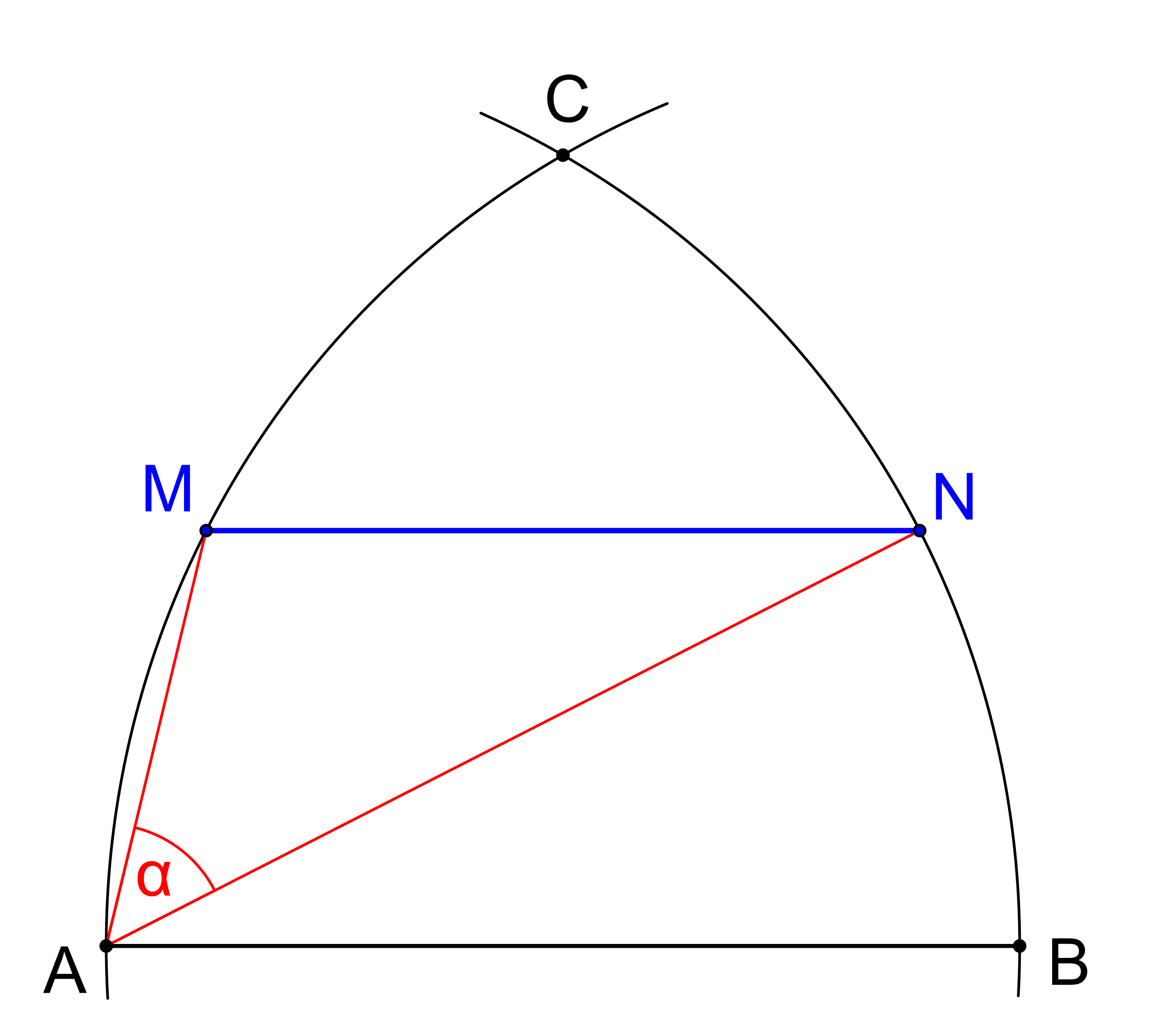
  PŘEDNÁŠKA 10 Skládání shodností. Shodnosti přímé a nepřímé. Grupa shodností. Prémiový úkol č. 10:  Dnešní prémiový úkol je věnován 180. výročí narození Josefa Rudolfa Vaňause (nar. 2. 5. 1839 v Komárově u Soběslavi), jednoho ze čtyř zakladatelů Jednoty českých matematiků a fyziků (zal. 28. 3. 1862). V roce 1902 zadal J. R. Vaňaus čtenářům Časopisu pro pěstování mathematiky a fysiky, ročník 31, číslo 3, následující úkol: Poloměrem AB opsány jsou z bodů A, B kruhové oblouky protínající se v bodě C. Ustanoviti jest v oblouku AC bod M a v oblouku BC bod N tak, aby MN bylo rovnoběžno k AB, a úhel MAN aby rovnal se danému ostrému úhlu. (viz Časopis pro pěstování mathematiky a fysiky, vol. 31, 3, Úloha 36, str. 262). Navrhněte postup řešení této úlohy.

• Stejnolehlost. Skládání stejnolehlostí v rovině. Stejnolehlost kružnic. Podobné transformace roviny.

  CVIČENÍ 11 Úlohy na shodnosti v rovině - Vzorové příklady KMA/PLA 2015

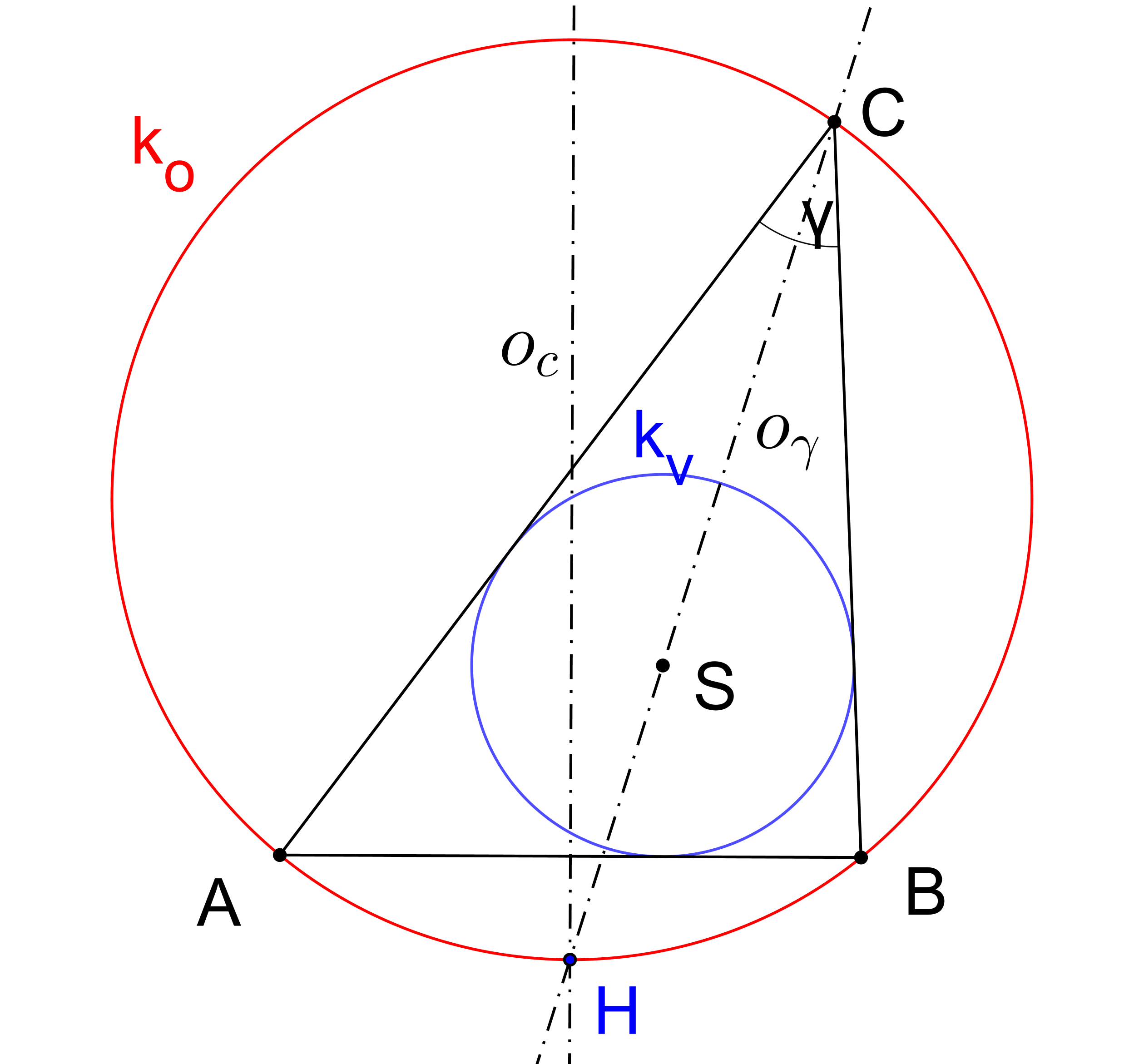
  PŘEDNÁŠKA 11 Klasifikace shodností v rovině. (Odvození analytického vyjádření afinity v rovině.) Shodnosti v rovině - úlohy. Prémiový úkol č. 11: Dokažte následující větu: Buď ABC trojúhelník takový, že |BC| je různé od |AC|. Potom osa úhlu ACB protíná osu strany AB v bodě H, který leží na kružnici trojúhelníku ABC opsané. Dále platí, že |HA|=|HB|=|HS|, kde S je střed kružnice trojúhelníku vepsané.

  CVIČENÍ 12 Stejnolehlost kružnic. Aplety: [Mongeova věta] [Eulerova přímka a kružnice devíti bodů] Stejnolehlost - úlohy k řešení. [Řešení vzorového příkladu č. 15 (bod-přímka-kružnice)] [Řešení vzorového příkladu č. 16 (bod-přímka-přímka)] [Řešení vzorového příkladu č. 17 (kružnice-přímka-přímka)]

  PŘEDNÁŠKA 12 Podobné zobrazení. Stejnolehlost. Skládání stejnolehlostí v rovině. Aplet: [Skládání stejnolehlostí] Podobnosti eukleidovské roviny.

• Shodnosti a podobnosti v konstrukčních úlohách.
• Mocnost bodu ke kružnici. Osová afinita.

  CVIČENÍ 13 Mocnost bodu ke kružnici - úlohy k řešení. [Řešení vzorového příkladu č. 1 užitím mocnosti bodu ke kružnici a pomocné kružnice] [Řešení vzorového příkladu č. 1 užitím mocnosti bodu ke kružnici a Eukleidovy věty o odvěsně]

  PŘEDNÁŠKA 13 Mocnost bodu ke kružnici.

Literatura

[1] Sekanina, M. a kol.: Geometrie II, SPN, Praha 1988.
[2] Pomykalová, E., Matematika pro gymnázia - Planimetrie. Prometheus, Praha, 2008.
[3] Kuřina, F.: 10 geometrických transformací. Prometheus, Praha, 2002.
[4] Sekanina, M. a kol.: Geometrie I, SPN, Praha 1988.
[5] Leischner, P. Geometrická zobrazení, Jihočeská univerzita v Českých Budějovicích, 2010.
[6] Pech, P., Klasické vs. počítačové metody při řešení úloh v geometrii, České Budějovice, PF JU, 2005.
[7] Kuřina, F.: 10 pohledů na geometrii. Akademie věd České republiky, 1996.
[8] Audin, M.: Geometry, Springer, 2003.
[9] Budinský, B.: Analytická a diferenciální geometrie. SNTL, Praha, 1983.
[10] Pech, P., Analytická geometrie lineárních útvarů, České Budějovice, PF JU, 2004.
[11] Voráčová a kol., Atlas geometrie. Geometrie krásná a užitečná. Academia, Praha, 2012.
[12] Vyšín, J. . a kol.: Geometrie pro pedagogické fakulty II, Bratislava, 1970.
[13] Eukleides, Eukleidovy základy (Elementa), překlad F. Servít, 1907.
Dostupné na https://commons.wikimedia.org/wiki/File:Eukleides_Servit.pdf
[14] Leydold, J., Petry, M. : Introduction to Maxima for Economics (pdf) [online]
[15]  Hašek, R., Noruláková, M.: Program wxMaxima ve výuce matematiky (pdf) [online]. Sborník příspěvků 5. konference Užití počítačů ve výuce matematiky, 2011.

Internetové odkazy

Software ke stažení

www.geogebra.org ... program GeoGebra (zdarma)
wxmaxima-developers.github.io/wxmaxima ... program wxMaxima (zdarma)

Materiály pro výuku a sebevzdělávání

i2geo.net ... portál pro sdílení výukových materiálů dynamické geometrie
wiki.geogebra.org ... GeoGebra Wiki - manuál, výukové materiály, fórum apod.
wiki.geogebra.org/cs/ ... postupně překládaná česká verze GeoGebra Wiki
www.youtube.com/user/GeoGebraChannel ... GeoGebra na YouTube
www.geogebratube.org ... Materiály v GeoGebře ke stáhnutí
www.cut-the-knot.org ... Interactive Mathematics Miscellany and Puzzles
http://www.math.uoc.gr ... Geometrikon - galerie geometrických témat

Požadavky na studenta

• Zkouška.
  • Zkouška má dvě části, písemnou a ústní, které se vykonávají v jeden den. Začíná se písemnou částí, ústní částí lze pokračovat pouze po úspěšném vypracování písemné části (tj. hodnocení nejhůře 3). Písemná část zkoušky se skládá ze tří příkladů (viz vzorové příklady), u konstrukčních úloh je kromě rozboru požadován popis konstrukce nebo její provedení, proto je vhodné přinést si rýsovací potřeby. Otázka k ústní části bude losována ze zveřejněných 12 otázek.
    [Otázky ke zkoušce KMA/PLA 2019] [Vzorové příklady KMA/PLA 2016]
    Řešení vzorového příkladu č. 1 (užití mocnosti bodu ke kružnici a pomocné kružnice)
    Řešení vzorového příkladu č. 1 (užití mocnosti bodu ke kružnici a Eukleidovy věty o odvěsně)
    Řešení vzorového příkladu č. 15 (bod-přímka-kružnice)
    Řešení vzorového příkladu č. 16 (bod-přímka-přímka)
    Řešení vzorového příkladu č. 17 (kružnice-přímka-přímka)
  • Podmínky řešení prémiových příkladů: Srozumitelný a přehledný zápis řešení problému, pochopitelně doplněný alespoň jedním obrázkem, můžete posílat během 1 týdne následujícího po dni zadání (zadání proběhne vždy na přednášce) na adresu hasek@pf.jcu.cz. Dokument obsahující řešení může mít libovolnou formu, od oskenování ručně psaného řešení až po text napsaný v textovém editoru. Vždy se však musí jednat o autentický text vypracovaný tím, kdo dokument posílá. Prvních pět autorů správných řešení bude odměněno zvýhodněním 0.25 klasifikačního stupně při hodnocení zkouškové písemky (Přehled řešitelů prémiových úkolů).